高误码率下Turbo码交织器的恢复方法
2015-10-13任亚博刘以农
任亚博 张 健 刘以农
高误码率下Turbo码交织器的恢复方法
任亚博*①②张 健②刘以农①
①(清华大学工程物理系 北京 100084)②((中国工程物理研究院电子工程研究所 绵阳 621900)
该文提出了一种针对高误码条件下Turbo码交织器的恢复方法,应用于码率为1/3的并行级联Turbo码。信道编码识别是非合作信号处理领域的重要内容,Turbo码交织器的恢复是其中的一个难点。现有的识别方法可以有效地处理无误码时的问题,而实际通信中Turbo码经常应用于信道质量较差的情况,此时误码率会较高,且码长较长,这些方法将失效。利用校验向量的特征,可将交织器的每个位置分离开来,单独求解,使得交织器中每个位置的恢复仅依赖于几个相关的位置,避免了误码累加效应,从而解决了在高误码率,长码长时的识别问题,其复杂度较低。在仿真结果中,对典型的长度达10000的随机交织器,接收序列10%误码率的情况下,实现了正确的恢复。
Turbo码;交织器;恢复
1 引言
信道编码用于纠正误码,在通信及存储中有着广泛的应用;在非合作通信中,由于其编码方式未知,就有了对信道编码识别的研究,近年来,这已成为一个研究热点。
Turbo码作为一种逼近香农限的码,近年来在3G, 4G及卫星通信中等得到了广泛的应用,Turbo码的识别也随之兴起。Turbo码完整的识别应包括卷积码的识别和随机交织器的识别,这两个问题可以分开处理,卷积码的识别已有较成熟的研究成果,本文专注于随机交织器的识别。文献[10]中提出了一种树状分枝的方法,该方法基于最大似然原理,即使在相当大噪声时也可以恢复出交织器,但这一方法对Turbo码还不够,因为其假设识别的对象是交织排列后的输出序列,而实际中接收到的是这一序列经过编码的序列。文献[11]提出了一种基于Turbo码译码的交织器恢复方法,该方法通过对比第位交织器正确恢复与不正确恢复时译码熵值的差异,来寻找第位的位置,是一种有效的方法,然而其算法中的Turbo译码,使其具有较高复杂度,随着交织器长度的增长,例如达10000时,在5%的误码率下的恢复也要几个小时,在10%的高误码率下几乎无法恢复。文献[12]提出了一种特别的方法,需假设信息序列无误码,通过将反馈卷积编码器的生成有理式(分子与分母均为多项式)作泰勒级数展开,可恢复出下一时刻交织后的数据,进而逐步恢复出整个交织器;当信息序列有误码时,作者提出了“剔除”和“纠正”两种策略,该策略对交织长度较长时,要求误码率非常低,其仿真表明,当长度为100时,有效识别的误码率在1%至2%。国内文献[13]提出了一种无误码条件下的盲识别方法,该法将编码后的序列除以生成有理式,从而恢复出交织后的信息序列,进行恢复出交织器,对有误码条件下的情况则没有提及。文献[14,15]中提出了对Turbo码码长与交织器的识别,其容忍的误码率也不到1%,交织器的长度只有几百。
现有的识别方法不能同时满足高误码率、长交织器的情况,而实际情况中的1/3并行级联Turbo码具备纠10%以上的误码率的能力,且其交织器的长度很长。针对这种情况,本文提出了一种逐位恢复交织器的方法,使得交织器中单个位置的恢复仅依赖于几个相关的位置,降低了问题的复杂度,最后的仿真结果印证了算法的有效性。
文章接下来的结构如下:第2节简要介绍Turbo码的编码原理,定义文中使用的符号,识别的模型;第3节给出误码条件下的识别算法,并分析算法的复杂度与一些参数的取值;第4节是仿真的结果;第5节给出结论。
2 Turbo码的识别模型
2.1 Turbo码的编码原理
典型的并行级联Turbo码的结构如图1所示。其中信息序列为,经过编码器1后得到的序列为;信息序列经过交织后得到,交织器的长度记为,编码后的序列为; 3路序列经过二进制对称信道后接收方得到的序列为,,。图中表示噪声,为一个0, 1序列,其中1的概率即为接收序列的误比特率(BER)。
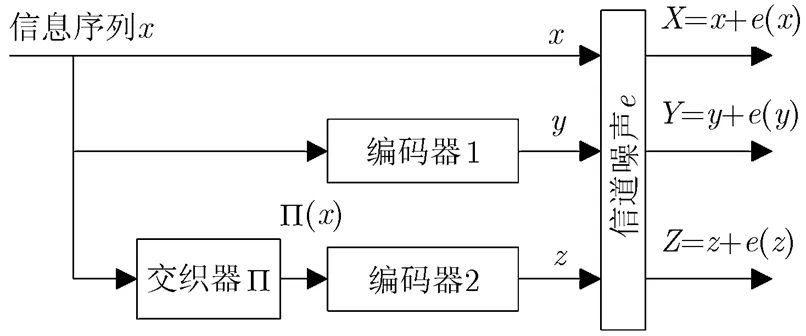
图1 Turbo码编码器
本文中关于Turbo编码的运算均是在GF(2)或其扩域上进行的。为方便描述,本文中的,,,,,以及后文出现的均为多项式,其形式例如。而,,分别表示关于,,的误码多项式。表示将多项式的系数按照交织器的规则置换后得到的新的多项式,若交织器表示的交织规则为,则,因此恢复交织器就是要计算出的取值。
假设反馈卷积编码器2的生成矩阵为,其中与为多项式,,,,每次编码前其移位寄存器初始的状态为0,则有式(1)成立
2.2识别的数学模型
将式(2),式(3),式(4)与式(1)结合有
误码条件下,如果误码率非常低(例如0.1%以下),交织器的长度比较短(例如只有几百),则序列中可能无误码,即,问题可转化为无误码条件下的识别问题。在一些条件下,如果误码率达1%甚至10%,或者Turbo码的交织器长度达几千甚至上万,这时就无法转化为无误码下的问题。
3 误码条件下交织器的恢复方法
3.1误码条件下的交织器恢复方法
式(5)进一步转化则有
假设通信的信道为二进制对称信道(BSC),其BER(转移概率)为,即多项式中系数为1的概率为。
式(12)提供了一种通过归纳法求解的方法。考虑到,通过对足够多的码字进行统计可以得到概率,其也小于0.5,显然对于任意的,应有。为已知量,同时,由式(7)知,故如果假设已知,则也为已知量,此时对未知的进行搜索,当的概率最小时,此时的即为最大似然的。于是有如下步骤恢复交织器的最大似然算法:
3.2算法的性能分析与参数取值
记
式中
于是整个交织器正确恢复的概率为
4 算法仿真结果
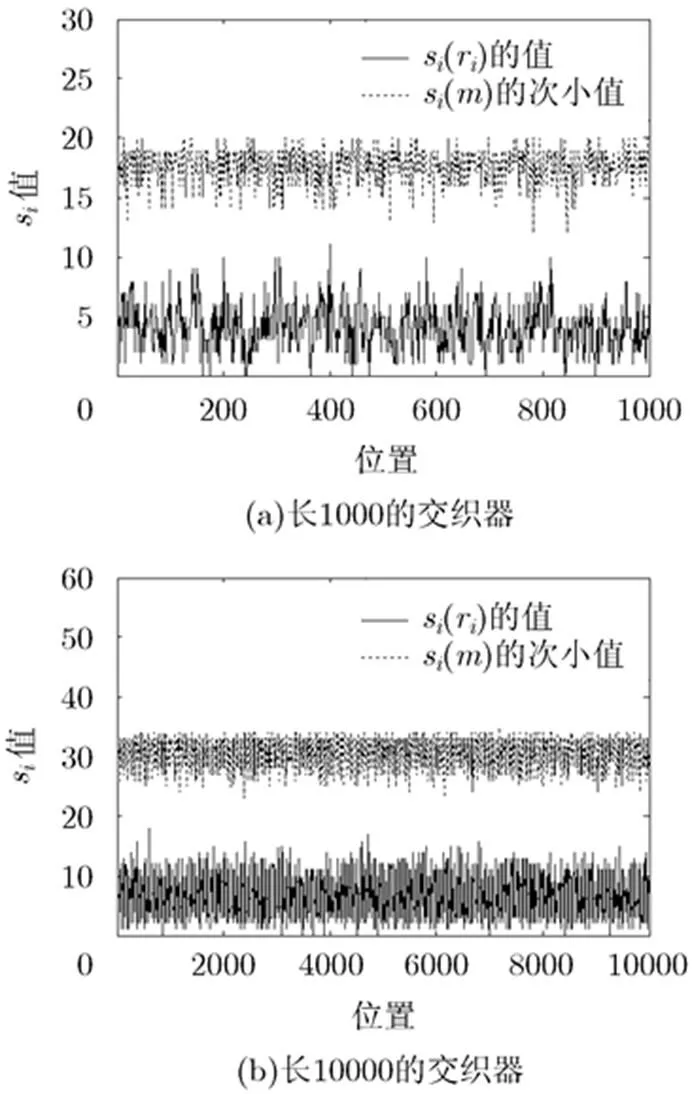
图2 1%误码下交织器恢复
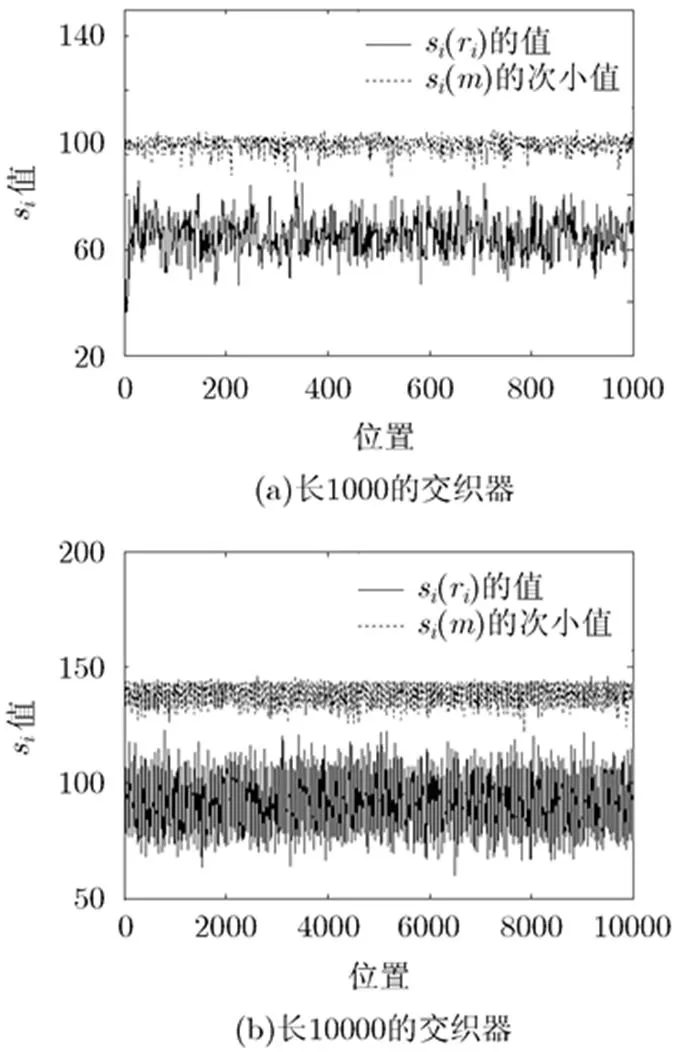
图3 5%误码下交织器恢复
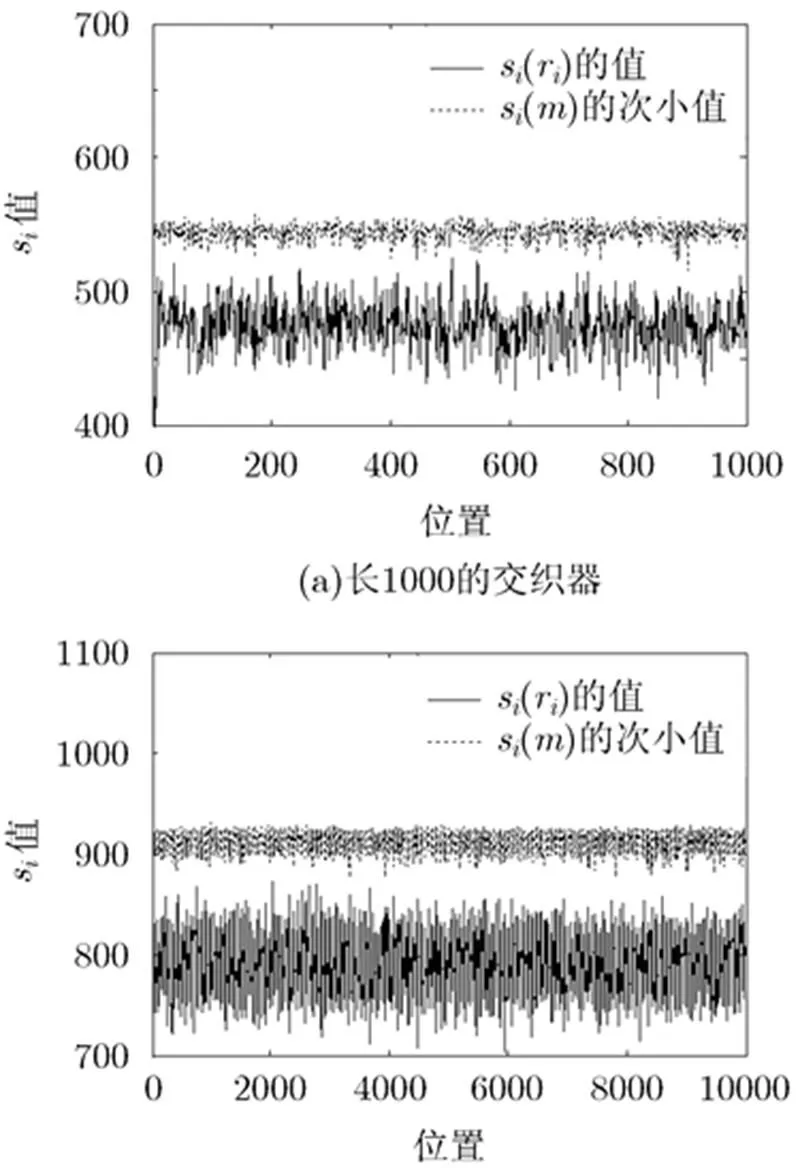
图4 10%误码下交织器恢复
仿真中的计算量与其它参数的选择如表1。表1反映出,当交织器增长,误码率增加时,识别所需要的码字数随之增长,这与理论分析一致。仿真中的计算来自于比特层次上的异或运算,在主频2.66 GHz的电脑上的运算时间,BER=1%时,对长度为1000的交织器识别时间不到1 s,而BER=10%,交织器长为10000时,用时约10 min。
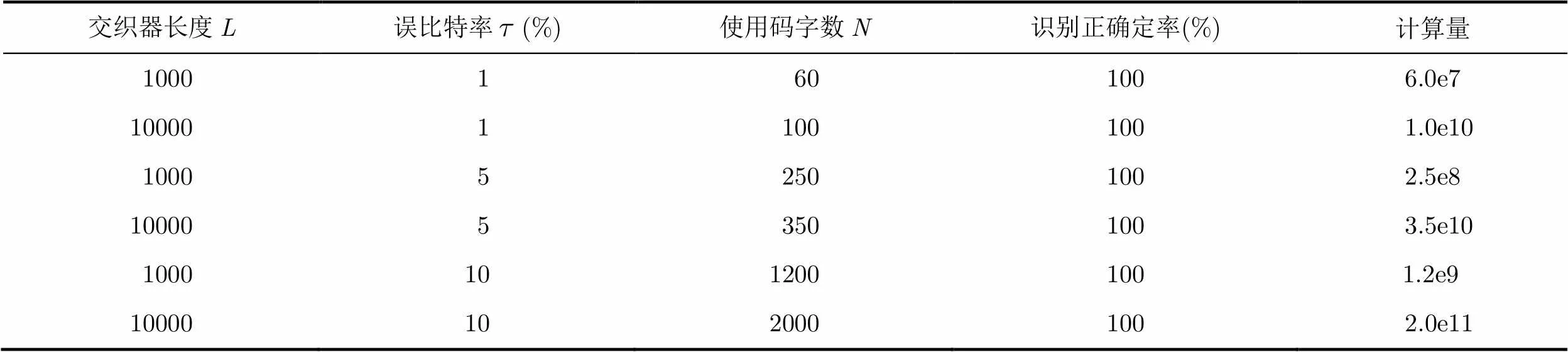
表1算法的参数选择与计算量
图5给出了当码字数目固定时,不同误码率下的识别正确率,在10%的误码率下都达到了100%的识别正确率,其识别正确率随着误码的增加而降低,识别错误率随着误码的增加而增加。图中“=1000,=1200”及“=10000,=2000”两条曲线很逼近,而“=1000,=2000”的效果明显优于两者,这说明当交织器的长度增长时,识别正确率会下降,但增大码字数目会提高识别正确率。
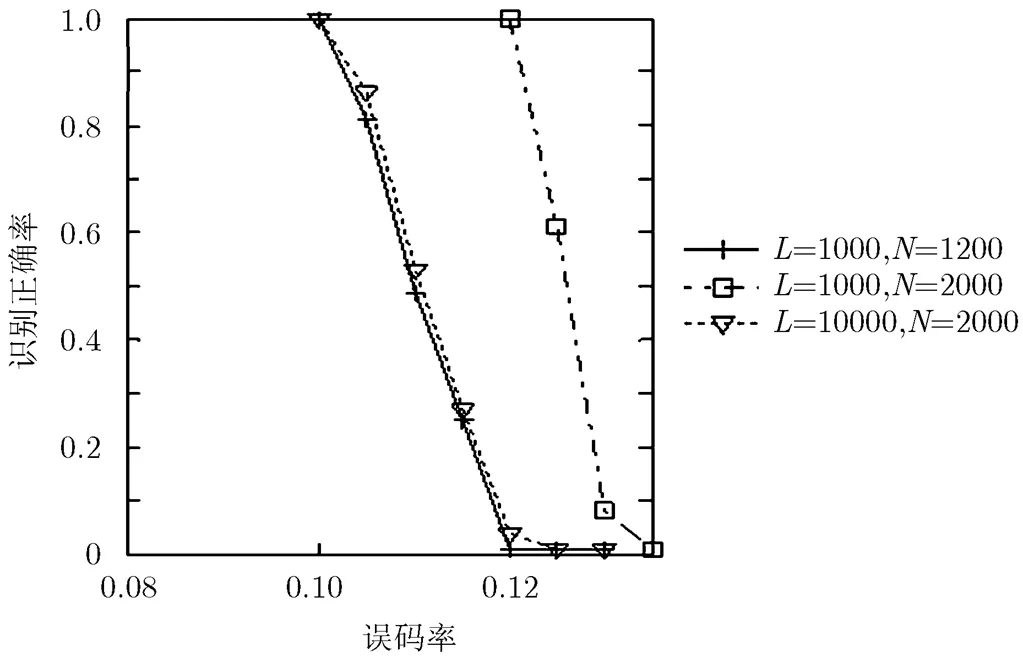
图5 不同误码率下的识别正确率
5 结论
Turbo码具有很强的纠错能力,近年来被广泛应用于低信噪比的信道中,对于1/3码率的Turbo码,本文提出的算法有效地解决了在10%的高误码下,随机交织器的恢复问题。从算法分析与仿真中可以看出,算法的存储量与计算量较小,在一般的电脑上即可运行,其识别时间较短,有较强的实用性。
参考文献
[1] 解辉, 黄知涛, 王丰华. 信道编码盲识别技术研究进展[J]. 电子学报, 2013, 41(6): 1166-1176.
Xie Hui, Huang Zhi-tao, and Wang Feng-hua. Research progress of blind recognition of channel coding[J]., 2013, 41(6): 1166-1176.
[2] Moosavi R and Larsson E G. A fast scheme for blind identification of channel codes[C]. IEEE Global Telecommunications Conference 2011, Linkoping, Sweden, 2011: 1-5.
[3] Bringer J and Chabanne H. Code reverse engineering problem for identification codes[J]., 2012, 58(4): 2406-2412.
[4] 闫郁翰. 信道编码盲识别技术研究[D]. [硕士论文], 西安电子科技大学, 2012.
[5] Marazin M, Gautier R, and Burel G. Algebraic method for blind recovery of punctured convolutional encoders from an erroneous bitstream[J].,2012, 6(2): 122-131.
[6] 于沛东, 李静, 彭华. 一种利用软判决的信道编码识别新算法[J]. 电子学报, 2013, 41(2): 301-306.
Yu Pei-dong, Li Jing, and Peng Hua. A new algorithm for channel coding recognition using soft decision[J]., 2013, 41(2): 301-306.
[7] 刘建成, 杨晓静. 基于校验统计的 (2, 1, m) 卷积码盲识别[J]. 电子信息对抗技术, 2013, 28(1): 1-4.
Liu Jian-cheng and Yang Xiao-jing. Blind recognition of (2,1,m) convolutional code based on parity-check Statistics[J]., 2013, 28(1): 1-4.
[8] Karimian Y and Attari M A. Recognition of channel encoder parameters from intercepted bitstream[C]. IEEE 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, 2013: 1-5.
[9] Moosavi R and Larsson E G. Fast blind recognition of channel codes[J]., 2014, 62(5): 1393-1405.
[10] Barbier J. Reconstruction of Turbo-code encoders[J]. SPIE, 2005, 5819: 463-473.
[11] Cluzeau M, Finiasz M, and Tillich J P. Methods for the reconstruction of parallel Turbo codes[C]. IEEE International. Symposium on Information Theory, Austin, TX, USA, 2010: 2008-2012.
[12] Cote M and Sendrier N. Reconstruction of a Turbo-code interleaver from noisy observation[C]. IEEE International Symposium on Information Theory, Austin, TX, USA, 2010: 2003-2007.
[13] 张永光. 一种Turbo码编码参数的盲识别方法[J]. 西安电子科技大学学报, 2011, 38(2): 167-172.
Zhang Yong-guang. Blind recognition method for the Turbo coding parameter[J]., 2011, 38(2): 167-172.
[14] 李啸天, 李艳斌, 昝俊军, 等. 一种基于矩阵分析的Turbo 码长识别算法[J]. 无线电工程, 2012, 42(4): 23-26.
Li Xiao-tian, Li Yan-bin, Zan Jun-jun,.. An algorithm for recognition of Turbo code length based on matrix analysis[J]., 2012, 42(4): 23-26.
[15] 李啸天, 张润生, 李艳斌. 归零Turbo 码识别算法[J]. 西安电子科技大学学报, 2013, 40(4): 161-166.
Li Xiao-tian, Zhang Run-sheng, and Li Yan-bin. Research on the recognition algorithm of Turbo codes on trellis termination[J]., 2013, 40(4): 161-166.
[16] Valembois A. Detection and recognition of a binary linear code[J]., 2001, 111(1): 199-218.
Reconstruction of Turbo-code Interleaver at High Bit Error Rate
Ren Ya-bo①②Zhang Jian②Liu Yi-nong①
①(,,100084,)②(,,621900,)
An algorithm to recover a Turbo-code interleaver is proposed at high Bit Error Rate (BER), and it is applied to the 1/3 parallel concatenated Turbo-code. The recognition of channel coding plays an important part in the field of non-cooperative signal processing; recovering a Turbo-code interleaver is one difficulty. There are already some effective algorithms for the noiseless condition, but in actual communication system, Turbo code is often used in a high noisy level, where the BER is high and the word length is long: these algorithms would be ineffective. Using the characteristic of the parity-heck vector, each position of the interleaver can be separated and solved independently. Thus, it makes the recovery of every position only rely on several correlative positions, which avoids the error accumulation effect. The algorithm solves the problem when the BER is high and the code length is long, and it also has low complexity. Simulations show that for a Turbo code with interleaver length 10000 and BER 10%, the algorithm runs successfully.
Turbo code; Interleaver; Reconstruction
TN911.22
A
1009-5896(2015)08-1926-05
10.11999/JEIT141556
任亚博 renyabo2005@126.com
2014-12-08收到,2015-03-23改回,2015-06-09网络优先出版
NSAF基金 (11176005)资助课题
任亚博: 男,1987年生,博士生,研究方向为信道编码识别.
张 健: 男,1968年生,研究员,博士生导师,研究方向为电子工程、无线通信、太赫兹.
刘以农: 男,1963年生,教授,博士生导师,研究方向为核电子学.
