钢悬链线立管触地段的结构循环应变响应实验研究
2015-10-13姜海洋高福平臧志鹏
姜海洋,高福平,臧志鹏
(中国科学院力学研究所,北京 100190)
立管系统是连接浮式海洋平台与水下生产系统的输送油气的海工结构。随着海洋油气开发由浅水向深水发展,钢悬链线立管(steel catenary riser,简称SCR)以其成本低、无需顶张力补偿、对浮体漂移和升沉运动的容度大等优点成为深水油田油气输送和注水管线经济有效的选择之一[1-2]。在海洋工程环境中,SCR立管顶端通过柔性接头悬挂于海洋平台,平台的漂移和垂荡引起立管的往复运动,引起立管触地段(touchdown zone,TDZ)形状不断改变,触地点(touch-down point,TDP)不断移动,使立管应变产生周期性变化。同时,由于立管与土体的相互作用及水流冲刷,床面产生沟槽,改变立管形状;这将使得立管局部应力分布发生变化,进而影响立管的疲劳寿命。已有研究表明,TDZ是钢悬链线立管较易发生疲劳破坏的区域[3]。
SCR立管在TDZ的往复运动会使立管正下方床面形成沿立管轴向的狭长沟槽,沟槽的形成与土体塑性变形及立管运动产生的水流使床面土体冲刷密切相关[4-7]。数值模拟计算则通常假设沟槽由土体的塑性变形产生[8-10],但研究未反映水流荷载对沟槽冲刷作用。已有模型实验表明,当加载端运动频率较小时,弯矩幅值随立管与土体拍击作用的发展而减小;而当频率较大时,幅值有增大趋势[11]。也有研究者采用数值模拟方法,研究了立管弯矩幅值随沟槽发展的规律[3,12]。但在以上关于立管与土体作用的研究均未考虑海底水流荷载的影响。Li等人[13]开展了SCR立管触地段冲刷实验研究,提出了最大冲刷深度的经验公式,却未考虑冲刷过程中立管弯矩幅值的变化。立管触地段的床面变形可影响立管结构的应力分布,进而对立管疲劳寿命产生影响[14]。可见,平台升沉运动以及海流冲刷等复杂条件引起的立管弯矩幅值变化规律有待于深入研究。
基于量纲分析理论和水槽模型实验,对典型工况下立管触地段的结构应变响应进行了物理模拟与分析,重点研究触地段床面形状变化对结构应变响应特性的影响。
1 量纲分析
SCR立管触地段的结构循环应变响应,涉及立管、海床以及海流之间的复杂的流固土动力耦合作用过程。立管循环应变幅值(εp)与立管、海流、海床的主要特征参量相关:

其中,各符号的物理含义及量纲,参见表1所示。
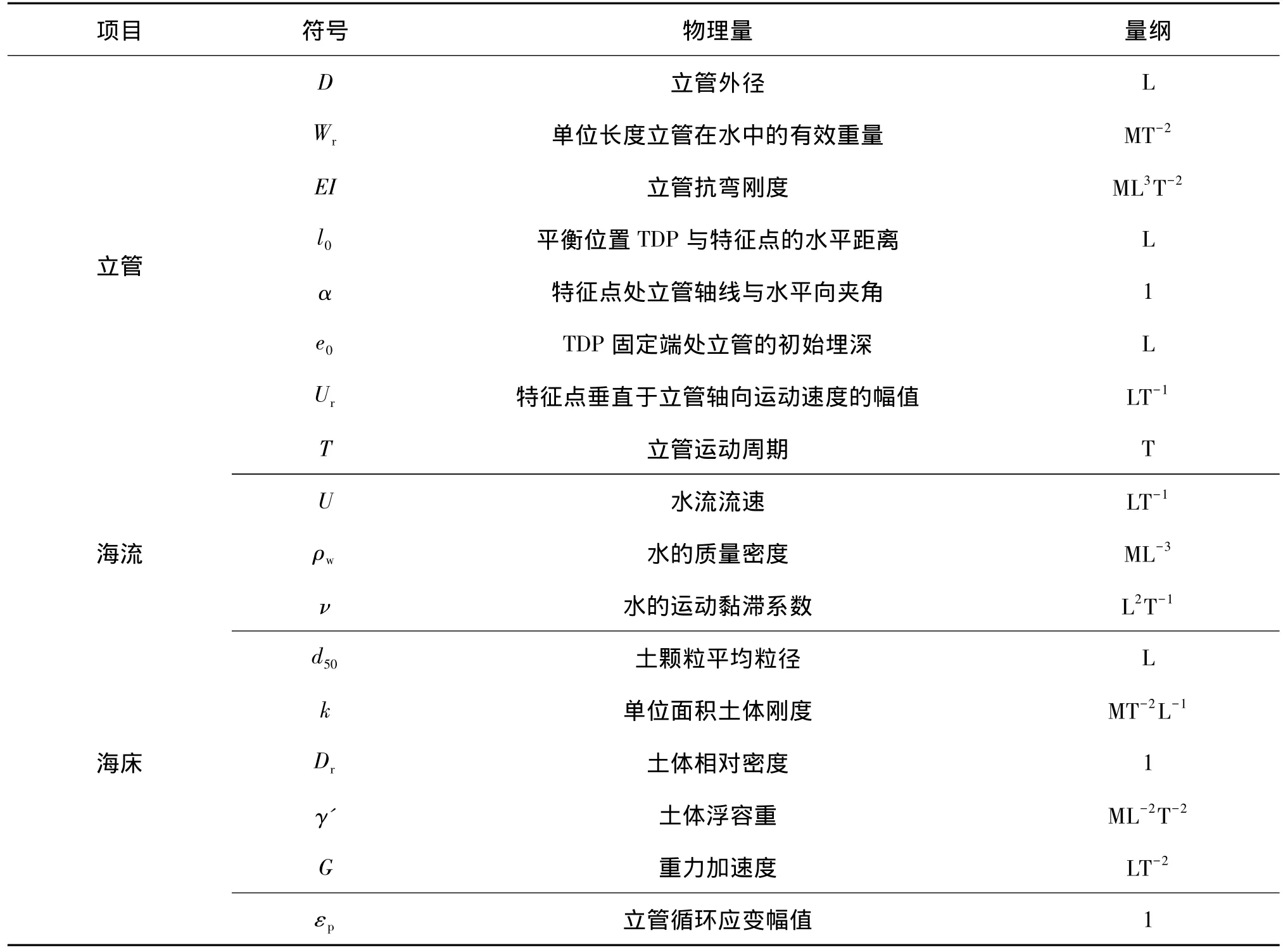
表1 SCR立管触地段的结构循环应变响应的主要特征参量Tab.1 Main influential parameters for cyclic strain responses of a SCR at its touch-down zone
选择D,g,ρw为基本参量,基于量纲分析理论,式(1)可表示为如下无量纲量的函数关系:




表2 主要物理量的相似关系Tab.2 Similarity relationship of the main physical quantities
2 实验装置及方法
专门设计了SCR立管与土体相互作用的实验模拟装置,搭建于流固土耦合水槽内(如图1所示)。该装置可模拟浮式平台升沉运动诱导的SCR立管TDP往复运动及其与水流和土体的动力耦合作用,并实现对流固土多物理参数的同步测量。流固土耦合水槽的双向造流系统可产生方向可调的水流。水槽中间试验段布置有长5.0 m、深0.5 m的土槽。鉴于SCR立管长径比通常较大,本实验研究采用截断试验模拟方法:将原型立管在TDZ上方截断,并利用机械加载装置对截断点进行位移控制,以简化模拟浮式平台升沉运动诱导的立管运动。模型立管安装于土槽一端,通过垫板厚度调整立管水平段的预埋深度;立管的另一端则铰接于竖向往复运动机构,可自动调节立管垂向运动的振幅和周期,实现模型立管上端的竖向正弦循环往复运动。

图1 SCR立管触地段与土体相互作用装置Fig.1 Experiment facility for SCR riser-soil interaction at touch-down zone
利用声学多普勒流速仪ADV测量立管特征点水平位置的(本实验中,立管特征点选取为立管中轴线上距床面1.0倍管径高度处)垂向4.5 cm和34.5 cm处及其上游2 m处的流速;利用非接触式运动测量系统测量立管特征点的运动;立管正上方外表面布有8个光纤测点,沿立管轴向均匀分布,间隔为0.5 m。每组实验开始前,使加载端立管的下表面与海床接触,将各测点应变设置为零。
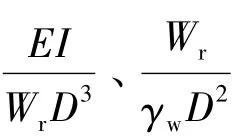
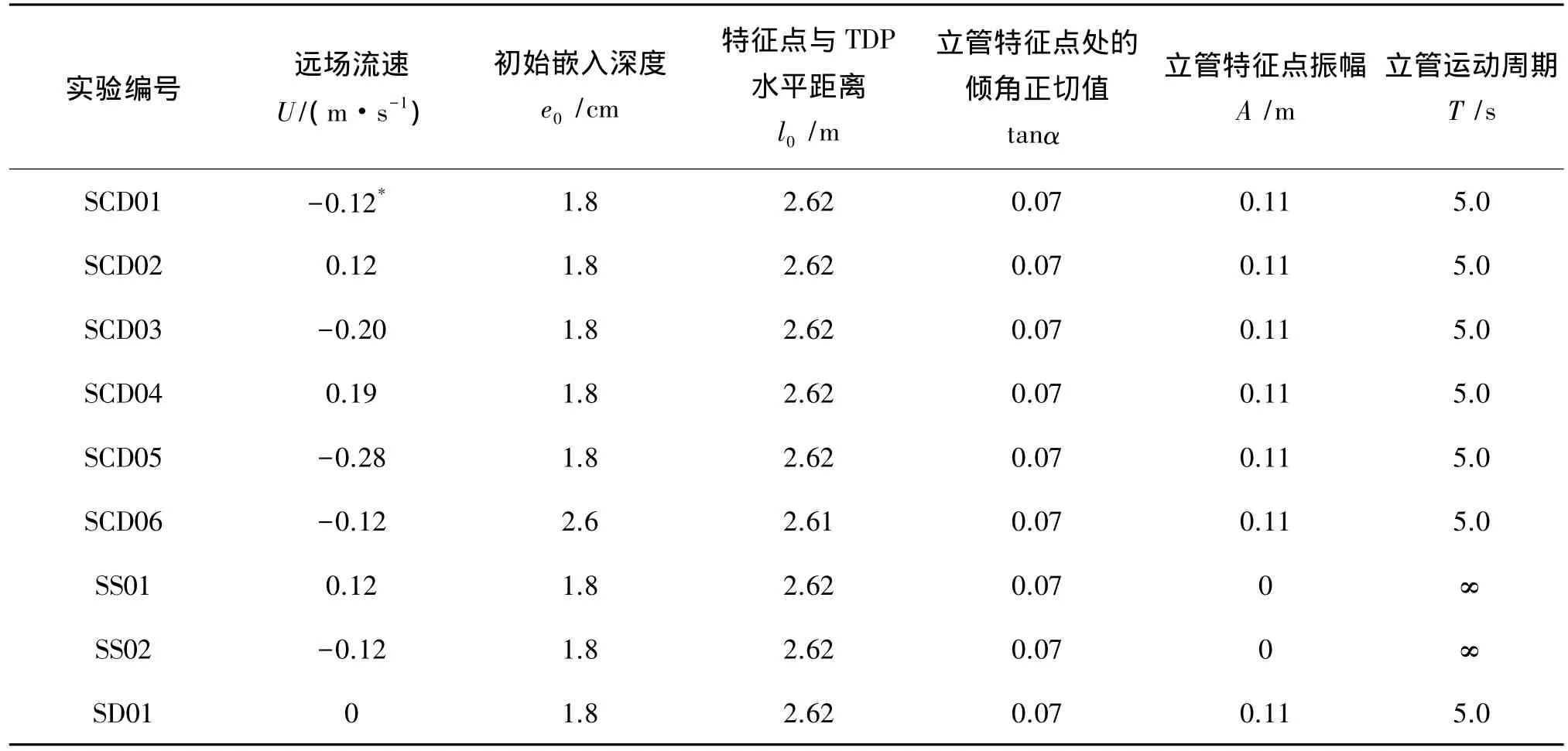
表3 系列水槽模型实验参数Tab.3 Test conditions for a series of flume experiments
3 实验结果及分析
3.1 立管触地段的局部冲刷形态
实验现象显示,对于无水流荷载的情况(U=0),仅在运动立管拍击作用下,立管下方土体形成的沟槽较浅,沟槽最大深度约为0.09倍管径。图2给出了e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.12(正向流)等参数条件下立管触地周围的冲刷地形情况。可见,在水流载荷下,运动立管下方沟槽则明显加剧:沟槽最大深度约为0.3倍管径;沟槽宽度由加载端到固定端逐渐减小,沟槽深度沿立管轴向分布呈现中部较大、两端较小的变化规律(见图2、图3),这与现场观测到的沟槽形状相符[17]。立管触地段的绕流流场特性实验表明,触地段除受到海床附近的底流作用外,立管结构的往复运动可产生周期性变化的二次振荡绕流,两者叠加使得立管触地段附近土体更易发生局部冲刷。
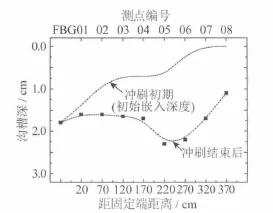
图2 冲刷前后立管正下方沟槽深度的变化(e0/D=0.16,KC=6.28,β =1.54×103,Frc=0.12,正向流)Fig.2 Variation of the trench depth vertically below the SCR before and after scour(e0/D=0.16,KC=6.28,β=1.54 × 103,Frc=0.12,forward current)

图3 冲刷结束后特征点附近床面照片(e0/D=0.16,KC=6.28,β =1.54× 103,Frc=0.12,正向流)Fig.3 The photograph of the soil near the feature point after scour(e0/D=0.16,KC=6.28,β =1.54× 103,Frc=0.12,forward current)
3.2 立管触地段的结构应变响应及分析
光纤应变传感器安装固定在模型立管上表面,加载端在最高点时立管上缘受压(应变为负值),在最低点时应变为正值。图4(a)给出了实验组SCD01中应变幅值最大测点FBG02的应变随时间变化。正、负循环应变极值分别用ε+、ε-表示,循环应变幅值用εp表示,即εp= ε+-ε-( )/2,如图4(b)所示。可见,FBG02的应变幅值随冲刷发展而逐步增大。
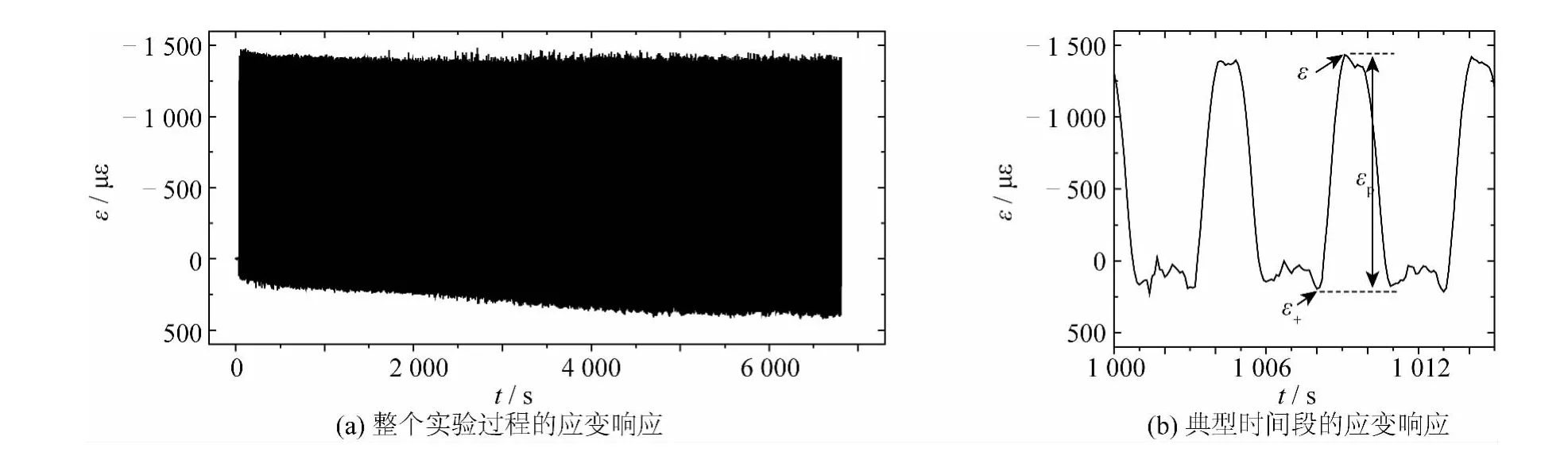
图4 应变幅值最大测点(FBG02)应变随时间变化(e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.12,逆向流)Fig.4 Variation of the maximum strain amplitude(FBG02)of the SCR versus time(e0/D=0.16,KC=6.28,β =1.54×103,Frc=0.12,reverse current)
图5给出了冲刷过程中所有测点的应变幅值变化。可以看出,εp最大值所在位置不随冲刷而改变(位于测点FBG02),各测点的εp随冲刷发展逐渐增大。在其它工况下,立管应变幅值呈现相同特征,局部冲刷使立管εp最大值有不同程度增大。图6给出了无水流荷载的运动立管和水流中运动立管应变幅值最大值(测点FBG02)随时间的变化情况。可见,无水流荷载的运动立管应变幅值更早趋于稳定值,且εp最大值小于水流中运动立管的工况。

图5 立管应变幅值分布随时间的变化(e0/D=0.16,KC=6.28,β =1.54×103,Frc=0.12,逆向流)Fig.5 Variation of the strain amplitude of the SCR versus time(e0/D=0.16,KC=6.28,β =1.54× 103,Frc=0.12,reverse current)
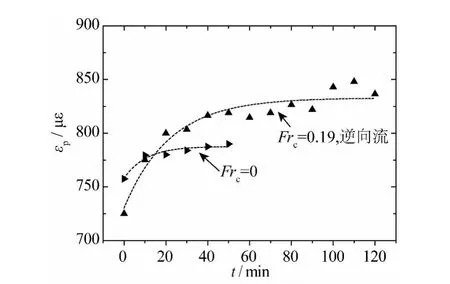
图6 立管最大应变幅值随时间的变化(e0/D=0.16,KC=6.28,β =1.54 × 103,FBG02)Fig.6 Variation of the maximum strain amplitude along the SCR versus time(e0/D=0.16,KC=6.28,β =1.54×103,No.02 fiber bragg grating)
3.3 床面变形对立管触地段应变幅值的影响
图7分别给出了每隔10 min FBG02的正负应变极值的变化。由图7可看出,冲刷后ε+增大268 με,ε-增大40 με,但小于ε+的增幅。因此,幅值εp随冲刷增大的主要原因是ε+的增大。图8给出了实验组冲刷初期和冲刷2 h后一个运动周期内FBG02的应变变化,以分析ε+随冲刷增大的原因;图9则对比了冲刷2 h后与图8同时刻的其它测点的应变响应情况。
从图8可看出,在立管运动的典型周期内,立管上部的拉应变幅值先逐渐减小;经历中间过渡区后,继而拉应变逐渐增大。冲刷2 h后的应变振荡幅值大于冲刷初期的幅值。受冲刷变形影响的立管应变突增幅值明显大于冲刷初期的应变振荡幅值。在接近冲刷变形最大处的立管(测点FBG02)拉应变突增程度最大,向两侧则逐渐减小(见图9):即距固定端越近(测点编号越小),则应变振荡幅值越小;距离加载端较近的测点(FBG05)的应变突增现象不明显。实验观察到的立管运动与实时应变数据对比表明,立管上缘拉应变突增发生在从立管触地段由最低点加速上升的瞬间。拉应变的突增幅度决定了正循环应变极值ε+的大小。与有水流荷载的工况相比,无水流荷载的运动立管实验结束后床面形状变化小,固定端附近管床间距小,因而最终的εp小于加载水流中运动立管情况。在本实验中,与冲刷初始阶段相比,冲刷2 h后的应变幅值的最大增幅可达25.9%。可见,在疲劳设计时若不考虑冲刷或沟槽对立管应变幅值的影响,则可能偏于危险。

图7 正应变极值和负应变极值随冲刷的变化(e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.19,逆向流,FBG02)Fig.7 Variation of the extreme positive and negative strain in the development of scour(e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.19,reverse current,No.02 fiber bragg grating)

图8 冲刷初期与冲刷2 h后的应变变化(e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.12,逆向流,FBG02)Fig.8 Variation of the strain at the beginning and 2 hours later of scour(e0/D=0.16,KC=6.28,β =1.54×103,Frc=0.12,reverse current,No.02 fiber bragg grating)

图9 冲刷2 h后各测点的应变变化(e0/D=0.16,KC=6.28,β=1.54×103,Frc=0.12,逆向流)Fig.9 Variation of the strain at fiber Bragg gratings for two hours duration of scouring(e0/D=0.16,KC=6.28,β =1.54×103,Frc=0.12,reverse current)
4 结语
1)设计了钢悬链线立管与海床动力耦合模拟装置。该装置搭建于流固土耦合波流水槽,可模拟浮式平台升沉运动诱导的SCR立管触地段往复运动及其与水流和土体冲刷的动力相互作用,并实现对流固土多物理参数的同步测试分析。
2)立管往复运动可产生周期性变化的二次振荡绕流,它与加载水流相叠加使得立管触地段附近土体更易发生局部冲刷;相应地,可引起SCR立管结构应力最大幅值的增大。
3)随着管土拍击作用和局部冲刷变形的发展,SCR立管触地段结构的循环应变幅值逐渐增大并趋于稳定值。由于固定端附近管段的悬跨及惯性,在立管脱离床面的瞬间观测到立管上缘的拉应变值突增现象。随着床面冲刷变形的发展,立管结构循环应变的变化幅值将逐渐增加。
[1] SONG R,STANTON P.Advances in deepwater steel catenary riser technology state-of-the-art:Part I-design[C]//Proceedings of 26th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers,2007:331-344.
[2] 白勇,龚顺风,白强,等.水下生产系统手册[M].哈尔滨:哈尔滨工程大学出版社,2012.(BAI Yong,GONG Shunfeng,BAI Qiang,et al.Manual for subsea production systems[M].Harbin:Harbin Engineering University Press,2012.(in Chinese))
[3] NAKHAEE A,ZHANG J.Trenching effects on dynamic behavior of a steel catenary riser[J].Ocean Engineering,2010,37(2):277-288.
[4] HU H J E,LEUNG C F,CHOW Y K,et al.Centrifuge modelling of SCR vertical motion at touchdown zone[J].Ocean Engineering,2011,38(7):888-899.
[5] WANG L,ZHANG J,YUAN F,et al.Interaction between catenary riser and soft seabed:Large-scale indoor tests[J].Applied Ocean Research,2014,45:10-21.
[6] BRIDGE C,HOWELLS H,TOY N,et al.Full-scale model tests of a steel catenary riser[J].Advances in Fluid Mechanics,2003,36:107-116.
[7] HODDER M S,BYRNE B W.3D experiments investigating the interaction of a model SCR with the seabed[J].Applied Ocean Research,2010,32(2):146-157.
[8] AUBENY C,BISCONTIN G.Interaction model for steel compliant riser on soft seabed[C]//Offshore Technology Conference.2008:paper No,194193.
[9] AUBENY C P,SHI H,MURFF J D.Collapse loads for a cylinder embedded in trench in cohesive soil[J].International Journal of Geomechanics,2005,5(4):320-325.
[10] GAO F P,WANG N,ZHAO B.Ultimate bearing capacity of a pipeline on clayey soils:Slip-line field solution and FEM simulation[J].Ocean Engineering,2013,73:159-167.
[11] ELLIOTT B J,ZAKERI A,BARRETT J,et al.Centrifuge modeling of steel catenary risers at touchdown zone part II:Assessment of centrifuge test results using kaolin clay[J].Ocean Engineering,2013,60:208-218.
[12]WANG K P,XUE H X,TANG W Y,et al.Fatigue analysis of steel catenary riser at the touch-down point based on linear hysteretic riser-soil interaction model[J].Ocean Engineering,2013,68:102-111.
[13] LI F Z,DWIVEDI A,LOW Y M,et al.Experimental investigation on scour under a vibrating catenary riser[J].Journal of Engineering Mechanics,2013,139(7):868-878.
[14] DET NORSKE VERITAS.Offshore standard DNV-RP-F204:riser fatigue[S].DNV Services,Research and Publications,Hovik,Norway,2010.
[15]PESCE C P,MARTINS C A,DA SILVEIRA L M Y.Riser-soil interaction:local dynamics at TDP and a discussion on the eigenvalue and the VIV problems[J].Journal of Offshore Mechanics and Arctic Engineering,2006,128(1):39-55.
[16] SUMER B M,FREDSøE J.Hydrodynamics around cylindrical structures[M].World Scientific,1997.
[17] BRIDGE C D,HOWELLS H A.Observations and modeling of steel catenary riser trenches[C]//Proceeding of 17th International Offshore and Polar Engineering Conference.2007:803-813.
