风场作用下的定日镜轻量化设计
2015-10-13冯煜陈小安谭惠文卓娅
冯煜,陈小安,谭惠文,卓娅
风场作用下的定日镜轻量化设计
冯煜,陈小安,谭惠文,卓娅
(重庆大学机械传动国家重点实验室,重庆,400044)
针对传统优化方法在定日镜轻量化设计中表现出的灵敏度依赖性和计算低效性等缺陷,提出将响应面模型与序列二次规划算法相结合的方法。该方法在保证定日镜强度、刚度和动态性能等要求的基础上,对风场作用下产生非线性响应的定日镜结构进行轻量化设计。通过数值风洞试验和Davenport谱得到作用在定日镜上的静态风荷载和脉动风频率,利用拉丁超立方试验设计得到的空间样本点进行数值仿真,建立各响应值关于15个设计变量的二阶响应面模型,并采用序列二次规划算法进行定日镜轻量化设计。研究结果表明:在保证定日镜满足许用挠度、应力和一阶固有频率的前提下,定日镜总质量减少了198 kg,减重率达12.31%,轻量化效果显著。同时该方法快速、高效、可靠,具有较强的工程实用性。
风场;定日镜;轻量化;响应面法;序列二次规划
定日镜是塔式太阳能热发电系统中的重要聚光设备,其不仅数量众多、占地面积巨大,而且是塔式太阳能热发电站的主要投资部分,其造价约占发电系统总造价的一半以上。在美国的Solar One中,定日镜投资占总投资的52%,在Solar Two中其建造费用也占电站总造价的50%以上[1]。因此,开展定日镜轻量化设计研究,对于降低定日镜建造成本、减小塔式太阳能电站投资和推动太阳能热发电技术商业化具有重要意义。针对定日镜轻量化技术难题,国内外学者已进行了大量研究。宫博等[2−3]采用灵敏度和均匀设计方法对定日镜结构进行优化设计。Pfahl等[4−6]对风荷载作用下定日镜的雷诺数进行了研究,并设计了一种通过减小镜面风荷载而实现减轻质量和降低成本的轻型定日镜。Blackmon[7]按不同的成本类别计算了定日镜每单位面积的最小化成本。但是,风场作用下的定日镜挠曲变形属于大位移、大变形的非线性过程,采用传统的基于灵敏度方法的轻量化设计面临着诸多困难:由于定日镜结构的复杂性,难以建立精确的物理模型,其目标函数和约束函数都难以显式化,同时目标函数和约束函数的导数大多数不连续;基于有限元法的结构优化无法快速准确获取各个参数的灵敏度信息,需不断进行结构的局部试探性对比分析计算,造成计算资源浪费,并且难以找到全局最优解等[8]。近年来,基于数理统计和试验设计的响应面优化设计方法已成为国内外学者研究的前沿和热点,文献[9−12]讨论了利用响应面法在汽车和机床等方面进行优化设计的问题。因此,本文作者通过数值风洞试验和Davenport谱进行定日镜风荷载模拟计算,并在拉丁超立方试验设计的基础上,利用响应面模型和序列二次规划算法对风场作用下产生非线性响应的定日镜结构开展轻量化设计研究。
1 风荷载特性分析
大量实测记录表明,顺风向风荷载时程曲线可看作由2部分组成:一种是周期在10 min以上的长周期平均风,另一种是周期只有几秒到几十秒的短周期脉动风。通常平均风的作用周期远大于定日镜的自振周期,因而其作用性质属于静力荷载,平均风是定日镜外荷载的主要形式。脉动风是由于风的不规则运动而引起的,可以视为一个具有零均值的各态历经平稳高斯随机过程,其作用周期与定日镜的自振周期较为接近,因而其作用性质属于随机动力荷载,脉动风是引起定日镜风振的主要因素。
1.1 平均风
大气边界层内的平均风速随着高度的增加而增大,且在不同的地面粗糙度条件下具有不同的变化规律。通常采用Davenport指数律来描述平均风速沿高度的变化规律,即
式中:z和v分别为标准参考高度和标准参考高度处的平均风速,取z=10 m;和v分别为任一高度和任一高度处的平均风速;为地面粗糙度指数。
1.2 脉动风
脉动风具有随机性,风速随时间和空间随机变化,在统计学上通常将其视为一个具有零均值的各态历经平稳高斯随机过程。GB 50009—2001“建筑结构荷载规范”[13]采用Davenport脉动风速谱来描述脉动风中各频率成分对应的能量分布规律:
同时,根据脉动风压功率谱定义和维纳−辛钦定理,可得脉动风压功率谱:
2 响应面方法
响应面法(RSM)是利用统计学综合试验技术解决复杂系统激励与响应关系的方法,其实质是对试验数据进行拟合,从而得到系统函数显式的近似表达式,来预测非试验点的响应值[15]。由于响应面法构造的近似函数无需解决求解偏导数难的问题,并且其近似函数的构造不涉及刚度矩阵和结构的具体分析过程,因此采用响应面法进行定日镜轻量化设计具有较强的通用性和独立性。图1所示为利用响应面方法进行定日镜轻量化设计的流程框图。
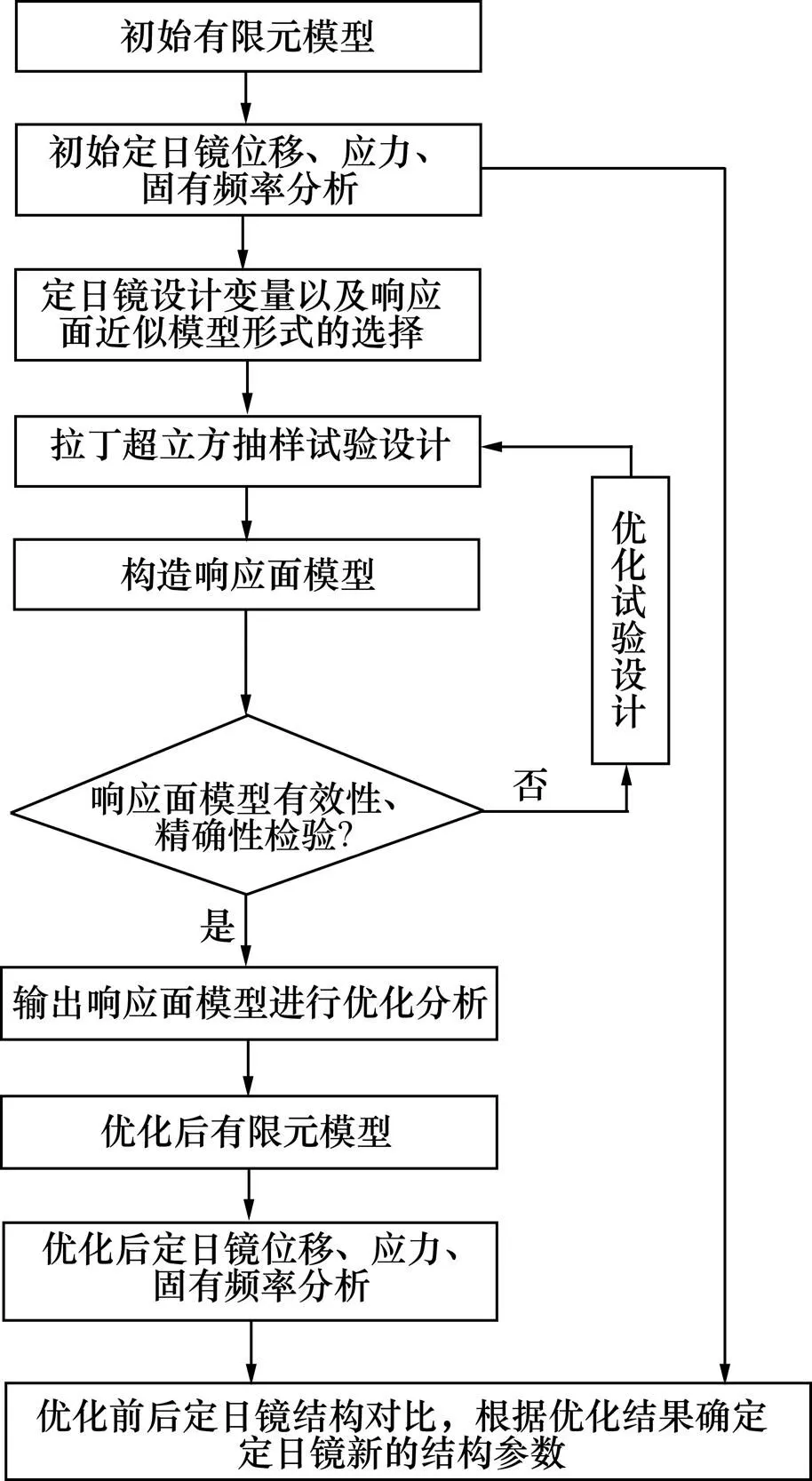
图1 基于响应面法的定日镜优化流程图
2.1 响应面模型
由于二阶多项式响应面模型能够灵活拟合系统的非线性,对真实响应的近似准确性较高,因此工程上常采用二阶多项式响应面模型。对个设计变量不含交叉项的二阶多项式响应面模型为
2.2 拉丁超立方试验设计
在响应面模型的构造过程中,试验设计点的选取对结果的有效性和精度影响很大,甚至直接决定整个定日镜轻量化过程的成败。拉丁超立方试验设计是一种约束随机生成均匀样本点的多维分层抽样技术,其估值稳定,且具有样本记忆功能,能避免重复抽取已出现过的样本,抽样效率高,均衡性能好,常用来安排多因素试验设计。拉丁超立方试验设计根据等概率随机正交分布原则,通过极少的试验点即可得到充满整个设计空间的高精度响应面近似模型,是用于大型设计空间中最有效的试验设计方法之一[17−18]。
2.3 响应面模型的精度检验
为了检验所得响应面模型的拟合精度和评估响应面模型的预测能力,根据统计学假设检验方法,采用拟合优度指标来评价响应面模型对试验数据的拟合精度。统计学中常采用决定系数2、调整决定系数、均方根误差(RMS)和值评估响应面模型的拟合、预测能力[19]。
式中:y为真实响应值;为真实响应值的均值。
2和的取值范围均为[0,1],2越接近1说明响应面模型的拟合逼近越精确,但是当响应面模型的项数增多时,响应面的剩余自由度减少,计算误差将被纳入到响应面模型中,2也接近于1。为避免错误判断,反映每项对模型精度的贡献,越大说明响应面精度越高。均方根误差反映了随机误差引起的输出量不均匀程度,其值越小越好。值表示响应面模型系数的显著性检验水平。
3 序列二次规划
序列二次规划(SQP)是处理中、小规模非线性优化问题的最优秀算法之一,它能在保持整体收敛性的同时保持局部超一次收敛。该算法的基本思想是基于拉格朗日函数二次近似的二次规划子问题,即在某个近似解处,将原非线性优化问题简化为求取一个二次规划问题的最优解,若有解则认为是原非线性优化问题的最优解,否则用近似解代替构成一个新的二次规划问题继续迭代。
对于一般的具有不等式约束的非线性优化问题,其二次规划子问题为
式中:为全变量搜索方向;c为拉格朗日函数的Hessian矩阵的正定拟牛顿近似矩阵。
在每一次主要迭代过程中,都要用BFGS法计算c。式(9)可以通过任意一种二次规划算法进行求解。
4 定日镜轻量化设计
定日镜轻量化设计是一个典型的有约束非线性最优化问题。风场作用下的定日镜需要在满足强度、刚度和固有频率等安全技术要求的前提下,设计出质量最轻且具有良好动静态特性的定日镜结构。根据我国对定日镜抗风设计的安全风速要求,即在6级风(风速为10.8~13.8 m/s,风压为73~120 Pa)作用下能正常工作而不影响聚光效率,在8级风(风速为17.2~20.7 m/s,风压为185~268 Pa)作用下不会发生风致倾覆和结构破坏,以兰州某地区(北纬36.058°)塔式太阳能电站为例,在电站容量设计点——春分日12:00工况下,镜场中某定日镜在重力荷载及6级风和8级风的风荷载作用情况下进行分析计算。
4.1 风荷载模拟计算
根据式(1)中的Davenport指数律平均风剖面形式,采用雷诺平均纳维−斯托克斯方程(RANS)和标准湍流模型[20]在FLUENT计算平台上利用计算流体动力学(CFD)方法进行定日镜在8级风和6级风环境中的数值风洞模拟实验。图2和图3所示分别为风速20.0 m/s和13.6 m/s时定日镜正面和背面的风压分布云图。

(a) 定日镜正面风压分布云图;(b) 定日镜背面风压分布云图
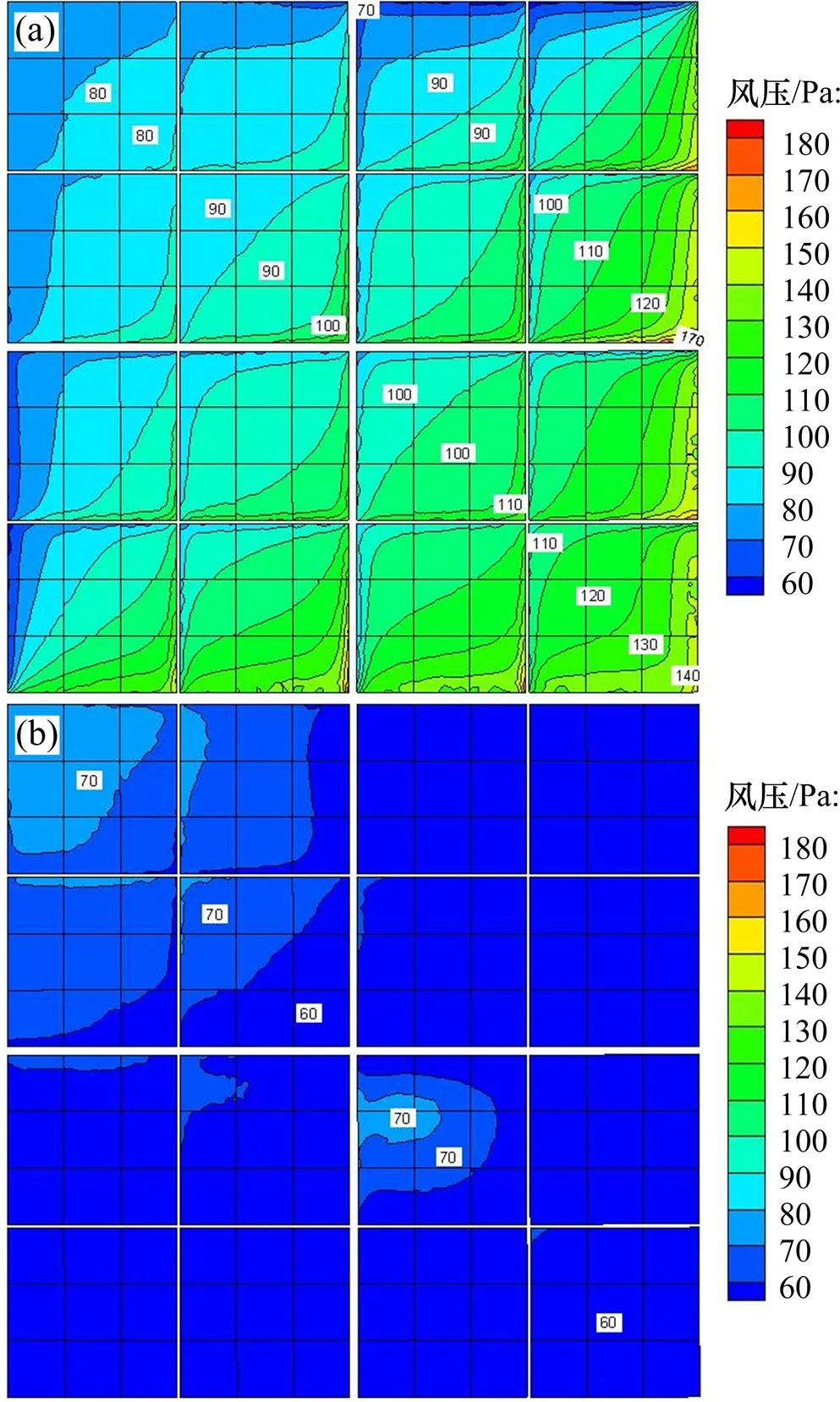
(a) 定日镜正面风压分布云图;(b) 定日镜背面风压分布云图
由图2和图3可见:在定日镜正面的迎风边缘处风压最大,且沿镜面风压从右下部到左上部呈逐渐递减变化;风流场绕过定日镜之后在其背面产生漩涡区,在背面的左上部和中间扭力管附近风压较大,其余部位相对较小。这与文献[21]所讨论的在迎风倾角作用下锥形建筑结构的风压分布规律相似。定日镜所受的风荷载即为正背面压力差所得到的净风压荷载,压力差越大静态风荷载越大。
当基本风速分别为20.0 m/s和13.6 m/s时,由式(2)和式(3)可得定日镜在5 m高度处脉动风的风速功率谱密度曲线和风压功率谱密度曲线,如图4和图5所示。

基本风速/(m∙s−1):1—20.0;2—13.6

基本风速/(m∙s−1):1—20.0;2—13.6
由图4和图5可知:风速、风压功率谱密度随着频率的增加而迅速衰减,脉动风的能量分布主要集中在0~0.5 Hz,当频率大于1 Hz时,脉动风的能量已经很小,可以忽略不计。因此,在考虑到定日镜质量的减小可能会使结构的一阶固有频率降低以及脉动风的倍频也可能会引起定日镜共振的基础上,设计频率3Hz为定日镜的最低频率约束。
4.2 响应面模型的构造拟合
定日镜镜架主要由不同截面尺寸的空间桁架结构、扭力管和侧板等组成。进行定日镜轻量化设计时,若设计变量过多将导致计算规模太大,优化效率降低,因此按照桁架结构的承载属性及空间层次,将空间桁架结构划分为6类,并分别选取主横梁、斜支梁、竖支梁、框架梁、连接梁Ⅱ和连接梁Ⅰ截面上等边槽钢的高度x(=1, 3, 5, 7, 9, 11)及其腿宽x(=2, 4, 6, 8, 10, 12),扭力管的直径13和壁厚14以及侧板厚度15,共15个设计变量,如图6所示。图7所示为进行定日镜轻量化设计分析的有限元模型,镜面采用太阳光透射比大于91%的4 mm厚的低铁超白太阳能玻璃,镜架材料为Q235。

图6 定日镜结构组成及设计变量定义

图7 定日镜有限元模型
采用拉丁超立方试验设计方法进行70次试验设计,并进行相应的有限元仿真分析,得到定日镜在每个样本点处的8级风作用下的镜面最大位移1、结构应力,6级风作用下的镜面最大位移2,以及振动的一阶固有频率的响应值。再根据试验点样本数据和响应值,利用最小二乘法原理进行响应面模型的拟合和精度检验。表1所示为响应面模型拟合值的精度检验结果。

表1 响应面模型拟合值精度检验
由表1可知:各响应面拟合值精度都很高,且都具有高度显著性,能够利用拟合的响应面模型进行预测分析和定日镜轻量化设计研究。
4.3 轻量化数学模型
通过对风场作用下定日镜的静力分析和模态分析可知:1) 由于定日镜镜面与支撑结构之间主要通过粘结陶瓷垫片、胶粘结、铆钉固定等方式进行连接,因此镜面最大应力恒为27.87 MPa,小于太阳能玻璃抗拉强度(太阳能玻璃抗拉强度为42 MPa),故不作为安全约束条件;2) 镜面的最大变形发生在迎风面边缘处,其他部位变形量相对较小,因此控制边缘处的最大变形量即可减小镜面的整体变形,满足定日镜的强度、刚度要求;3) 定日镜的一阶固有频率为4.075 Hz,可进一步进行频率优化达到效果最优。基于以上分析,定日镜轻量化设计的数学模型为:
式中:()为定日镜的总质量;lim为风荷载标准值作用下的镜面挠度极限值。根据GB 50009—2001“建筑结构荷载规范”计算得垂直于镜面的风荷载标准值0.52 kN/m2,实际风荷载值0.405 kN/m2,小于风荷载标准值,则按风荷载标准值计算的镜面挠度极限值是偏安全的,计算得lim=19.5 mm。
4.4 优化过程及结果
利用定日镜轻量化数学模型,采用序列二次规划算法(SQP)对目标函数进行优化求解。图8所示为轻量化定日镜总质量随迭代次数的变化曲线。由图8可知:经过30次迭代计算即得到稳定的收敛结果,可见SQP法计算效率非常高。表2所示为定日镜优化前后的结果对比。由表2可知:采用基于响应面模型的定日镜轻量化设计后,定日镜在8级风作用下的镜面最大位移1和结构最大应力都控制在设计要求的安全范围内,且比初始值分别减小了8.84%和31.58%,6级风作用下的镜面最大位移2比初始值减小了8.26%,同时定日镜的一阶固有频率提高了5.52%,而定日镜总质量减小了198 kg,减重率达12.31%,取得了显著的轻量化效果。

图8 轻量化定日镜总质量随迭代次数的变化曲线

表2 定日镜优化前后结果对比
为了分析设计变量对定日镜各响应值的影响程度,便于定日镜轻量化结果修正和二次设计,根据响应面模型可得定日镜各响应值对15个设计变量的灵敏度,如图9所示。
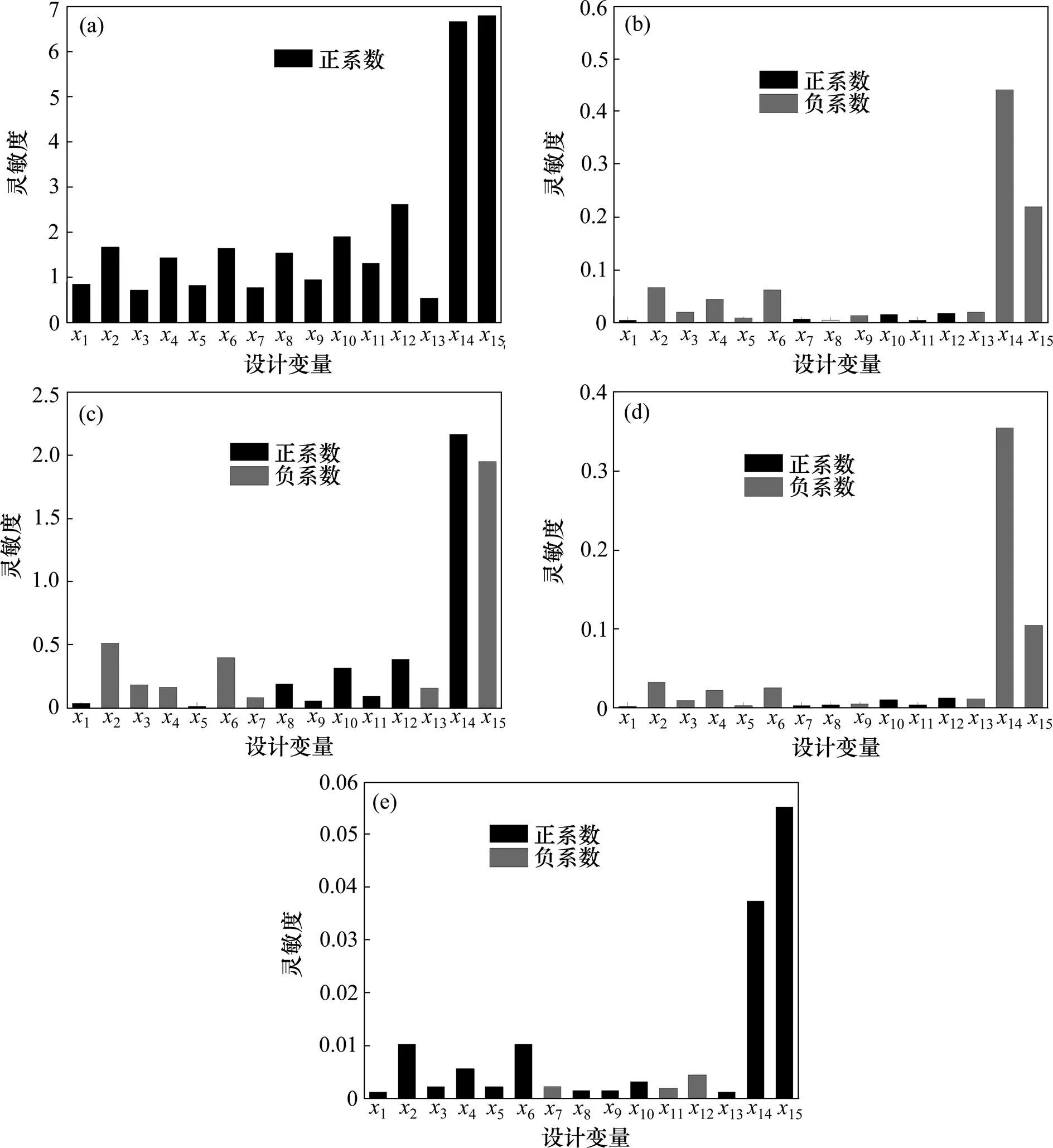
(a) 定日镜质量M对设计变量的灵敏度;(b) 镜面挠度U1对设计变量的灵敏度;(c) 结构应力σ对设计变量的灵敏度;(d) 镜面挠度U2对设计变量的灵敏度;(e) 定日镜一阶固有频率f对设计变量的灵敏度
由图9可知:定日镜质量跟各设计变量都呈正相关,其中,扭力管壁厚14和侧板厚度15对定日镜轻量化设计影响最大。同时,14对定日镜镜面挠度1和2的负影响最大,15对结构应力和定日镜一阶固有频率的影响最大,是整个定日镜轻量化设计过程中需要重点控制调整的参数。而设计变量1,5,7,8,9和11对定日镜各响应值影响相对较小。
5 结论
1) 通过数值风洞模拟试验和Davenport谱进行风荷载特性分析,计算出作用在定日镜上的静态风荷载和脉动风功率谱,得到定日镜风场作用模型。
2) 利用拉丁超立方试验设计方法只需通过选取极少试验点即可得到充满整个设计空间的高精度响应面近似模型的特性,并用以安排设计变量的多因素 试验。
3) 将响应面模型与序列二次规划算法相结合的轻量化设计方法模型建立简单、预测能力强、优化效率高,计算结果精确可靠,具有较强的工程实用性。
4) 在保证定日镜满足强度、刚度和动态性能等要求的基础上,实现定日镜总质量减少了198 kg,减重率达12.31%,取得了显著的轻量化效果。扭力管壁厚和侧板厚度的灵敏度系数较大,是定日镜轻量化设计中需要重点控制调整的参数。
[1] 郭苏, 刘德有, 张耀明, 等. 塔式太阳能热发电的定日镜[J]. 太阳能, 2006(5): 34−37. GUO Su, LIU Deyou, ZHANG Yaoming, et al. Heliostat of Solar thermal power tower[J]. Solar Energy, 2006(5): 34−37.
[2] 宫博, 李正农, 王莺歌, 等. 定日镜结构优化分析[C]// 崔京浩. 第18届全国结构工程学术会议论文集(第Ⅲ册). 北京:工程力学, 2009: 359−362. GONG Bo, LI Zhengnong, WANG Yingge, et al. Optimum analysis of structures on heliostat[C]// CUI Jinghao. Proceeding of the Eighteenth National Conference on Structural Engineering(Ⅲ). Beijing: Engineering Mechanics, 2009: 359−362.
[3] 李正农, 梁笑寒, 吴卫祥, 等. 基于均匀设计与线性回归的定日镜结构优化设计[J]. 湖南大学学报(自然科学版), 2012, 39(12):1−6. LI Zhengnong, LIANG Xiaohan, WU Weixiang, et al. Research on the optimization design of heliostat structure based on uniform design and linear regression[J]. Journal of Hunan University (Natural Sciences), 2012, 39(12): 1−6.
[4] Pfahl A, Uhlemann H. Wind loads on heliostats and photovoltaic trackers at various Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(9): 964−968.
[5] Pfahl A, Buselmeier M, Zaschke M. Wind loads on heliostats and photovoltaic trackers of various aspect ratios[J]. Solar Energy, 2011, 85(9): 2185−2201.
[6] Pfahl A, Randt M, Holze C, et al. Autonomous light-weight heliostat with rim drives[J]. Solar Energy, 2013, 92: 230−240.
[7] Blackmon J B. Parametric determination of heliostat minimum cost per unit area[J]. Solar Energy, 2013, 97: 342−349.
[8] 梁醒培, 王辉. 基于有限元法的结构优化设计: 原理与工程应用[M]. 北京: 清华大学出版社, 2010: 10−68. LIANG Xingpei, WANG Hui. Structural optimization: Principles and engineering applications[M]. Beijing: Tsinghua University Press, 2010: 10−68.
[9] 张勇, 李光耀, 钟志华. 基于移动最小二乘响应面方法的整车轻量化设计优化[J]. 机械工程学报, 2008, 44(11): 192−196. ZHANG Yong, LI Guangyao, ZHONG Zhihua. Design optimization on lightweight of full vehicle based on moving least square response surface method[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11): 192−196.
[10] 潘锋, 朱平. 面向约束优化的改进响应面法在车身轻量化设计中的应用[J]. 机械工程学报, 2011, 47(10): 82−87. PAN Feng, ZHU Ping. Improved response surface method for constrained optimization and its application to lightweight design of autobody structures[J]. Journal of Mechanical Engineering, 2011, 47(10): 82−87.
[11] 姜衡, 管贻生, 邱志成, 等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125−133. JIANG Heng, GUAN Yisheng, QIU Zhicheng, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11): 125−133.
[12] 于海莲, 王永泉, 陈花玲, 等. 响应面模型与多目标遗传算法相结合的机床立柱参数优化[J]. 西安交通大学学报, 2012, 46(11): 80−85. YU Hailian, WANG Yongquan, CHEN Hualing, et al. Optimization for machine tool column combining response surface model with multi-objective genetic algorithm[J]. Journal of Xi’an Jiaotong University, 2012, 46(11): 80−85.
[13] GB 50009—2001, 建筑结构荷载规范[S]. GB 50009—2001, Load code for the design of building structures[S].
[14] 王修琼, 崔剑峰. Davenport谱中系数的计算公式及其工程应用[J]. 同济大学学报(自然科学版), 2002, 30(7): 849−852. WANG Xiuqiong, CUI Jianfeng. Formula of coefficientin expression of davenport spectrum and its engineering application[J]. Journal of Tongji University (Natural Science), 2002, 30(7): 849−852.
[15] Myers R H, Montgomery D C, Vining G G, et al. Response surface methodology: A retrospective and literature survey[J]. Journal of Quality Technology, 2004, 36(1): 53−57.
[16] Ahn J, Kim H J, Lee D H, et al. Response surface method for airfoil design in transonic flow[J]. Journal of Aircraft, 2001, 38(2): 231−238.
[17] Morris M D, Mitchell T J. Exploratory designs for computational experiments[J]. Journal of Statistical Planning and Inference, 1995, 43(3): 381−402.
[18] 刘晓路, 陈英武, 荆显荣, 等. 优化拉丁方试验设计方法及其应用[J]. 国防科技大学学报, 2011, 33(5): 73−77. LIU Xiaolu, CHEN Yingwu, JING Xianrong, et al. Optimized Latin hypercube sampling method and its application[J]. Journal of National University of Defense Technology, 2011, 33(5): 73−77.
[19] 何正风. MATLAB概率与数理统计分析[M]. 北京: 机械工业出版社, 2012: 22−58. HE Zhengfeng. Analysis of probability and mathematical statistics by MATLAB[M]. Beijing: China Machine Press, 2012: 22−58.
[20] Juretic F, Kozmar H. Computational modeling of the neutrally stratified atmospheric boundary layer flow using the standard–turbulence model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 115: 112−120.
[21] Ikhwan M, Ruck B. Flow and pressure field characteristics around pyramidal buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(10): 745−765.
Lightweight design of heliostat in wind field
FENG Yu, CHEN Xiaoan, TAN Huiwen, ZHUO Ya
(The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)
In view of the sensitivity of dependence and computational inefficiency in traditional optimization methods for lightweight design of heliostat, an approximate optimization approach combining response surface model with sequential quadratic programming was proposed to deal with the lightweight design of heliostat which has nonlinear response with the action of wind based on guaranteeing the strength, stiffness and dynamic property of heliostat. Then, static wind load and fluctuating wind frequency were respectively obtained by numerical wind tunnel test and Davenport power spectrum. The Latin hypercube experimental design scheme and the response surface method were combined to construct the second-order response surface models by fitting with 15 design parameters. Furthermore, the response surface models were optimized by using the sequential quadratic programming. The results show that the total mass of heliostat is decreased by 198 kg, lightweight rating is 12.31% under the condition of ensuring the allowable deflection, stress and first-order natural frequency, and the effect of lightweight is remarkable. In addition, the approach is rapid, efficient and reliable, and it has strong engineering practicability.
wind field; heliostat; lightweight; response surface method; sequential quadratic programming
10.11817/j.issn.1672-7207.2015.05.046
TK513.1
A
1672−7207(2015)05−1915−08
2014−05−23;
2014−08−13
国家自然科学基金资助项目(51075407);重庆市研究生科研创新项目(CYB14010) (Project(51075407) supported by the National Natural Science Foundation of China; Project(CYB14010) supported by Chongqing Graduate Student Research Innovation Project)
陈小安,博士,教授,博士生导师,从事机械设计理论及实验方法研究;E-mail: xachen@cqu.edu.cn
(编辑 赵俊)
