考虑下部结构支承刚度的大跨度屋盖风致响应分析

陈智勇，彭振斌，陈伟



考虑下部结构支承刚度的大跨度屋盖风致响应分析

陈智勇1，彭振斌1，陈伟2

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 广州工程总承包集团有限公司，广东广州，510030)

在对广州国际体育演艺中心实施刚性测压模型风洞实验的基础上，对分别采用整体模型与简化整体模型对其上部大跨度空间屋盖钢结构的风致动力响应进行对比分析与研究。同时，在分析结构风致振动响应计算方法时，分别采用传统的多阶自由振动模态和基于荷载的Ritz向量模态进行对比分析，其中基于荷载的Ritz向量求解所需的初始荷载模式通过本征正交分解(POD)技术获得。研究结果表明：简化整体模型风致响应的计算结果比整体模型的风致动力响应稍大，其主要原因是在采用相同数目的参振模态时，简化整体模型所包含的对屋盖风致响应有直接贡献的模态比整体模型的模态多；所提出的基于屋盖表面风荷载的Ritz向量法求解仅使用少数参振模态，即可获得传统模态叠加法同样精度的风致振动响应，说明该方法是有效的。

大跨屋盖结构；风致响应；Ritz向量；POD分解

一般的大跨度体育场馆主要由上部的大跨度空间屋面和其下部支承的混凝土框架结构看台和辅助用房组成，上、下部结构之间通过屋盖底部支座相连接。由于下部混凝土结构组成一般复杂，杆件众多，因此，在进行上部屋盖风致响应分析时，若计算模型将上部屋盖和下部支承混凝土结构全部计入，则有限元计算和屋盖风致振动分析的工作量很大。考虑到体育场馆中结构自身的组成特点，其上部大跨度空间结构与下部支承混凝土结构相比刚度要小得多，因此，仅考虑以上部大跨度空间结构本身为基础的简化整体模型，并考虑上部屋盖和下部混凝土支承结构的相互作用，这样既可以考虑上、下部结构两者之间的共同作用，又可以大大减少大跨屋盖风振响应计算的工作量[1−2]。另外，大跨度屋盖结构由于采用轻质高强材料，在屋盖自重降低的同时，结构刚度也日趋变柔，使得其对风的敏感性日益增强，风荷载已成为该类结构设计中的主要控制荷载。其表面风荷载具有明显的三维特征，本征正交分解(POD)方法作为一种有效描述大跨屋面风荷载分布状况的有效工具[3−7]，是空间时间分离的分析方法。Holmes等[3]应用POD分析了脉动压力场。另一方面，大跨度体育场馆屋盖结构本身存在振动模态密集、振型间耦合效应明显等特点，高阶模态对结构风致响应不可忽略，甚至部分高阶模态贡献很大的现象。应用以传统振型分解理论为基础的频域分析方法时，较难有效处理计算振型数量和保证必要的计算精度。众所周知，衡量1个振型对结构动力响应的程度由下述2个条件共同决定：1) 振型形状是否与荷载的空间分布形式类似；2) 该振型对应的频率与荷载的中心频率接近程度。由Wilson等[8]提出的WYD (Wilson Yuan Dickens)法所采用的Ritz向量直接叠加法正是根据这2个条件来选择初始Ritz向量。基于荷载的Ritz向量考虑了荷载的空间分布特点，只需少数Ritz向量即可保证振动响应分析精度，从而显著提高计算效率。Gu等[9]对WYD进行了改进，发展了与荷载频率相关的Ritz向量叠加法，李方慧等[10−13]对运用Ritz法对大跨屋盖结构的抗风设计进行了相关论述。对于大跨屋盖风致动力响应分析，Ritz向量叠加法的一个关键问题是如何得到荷载的空间分布形式。通过本征正交分解法(POD)法，可以用较少的几组本征模态作为Ritz模态分析的初始荷载向量，得到基于风荷载POD分解的Ritz模态振型，进行后续的随机振动分析[14]。本文以广州国际演艺中心大跨度屋盖为例，在考虑下部混凝土支承体系共同作用下对其上部大跨度空间屋盖的风致动力响应进行研究。同时，在用频域法进行的风致响应计算中，分别采用多阶传统自由振动模态和数量较少的基于屋盖风荷载分布特征的块Ritz向量模态进行分析。

1 工程概况及结构体系

广州国际体育演艺中心模型见图1，它为符合NBA(National basketball association)和AEG(Anschutz entertainment group)标准的大型综合性体育场馆，总建筑面积约 12 万m2，建筑高度为34.5 m。该体育馆由屋面钢结构屋架和下部混凝土主体结构组成(图1(a))，两者之间采用具有一定水平滑移和转动刚度的橡胶支座连接。上部屋架长×宽为136 m×106 m的钢桁架结构，纵横桁架正交分布，其主要由10榀跨度为79.7~106.2 m、高为8.2~12.1 m的主桁架和两榀跨度为136.2 m、桁架高为11.8 m的次桁架组成。图1(b)所示为其上部屋盖部分的SAP2000有限元模型。下部混凝土结构体系对上部大跨度钢结构屋盖结构的支承作用，采用设计单位提供的如表1所示的支承刚度(如图1(b)中底部支座部分)进行模拟。

(a) 广州体育演艺中心主体育馆整体模型；(b) 主体育馆上部屋盖SAP2000有限元模型

表1 广州国际体育演艺中心屋盖下部支座支承刚度

2 风洞实验概述

新乡医学院点加团队结合自身和本校的实际情况，在探索“科研团队——小组二元育人模式”的过程中，取得诸多成绩的同时并发现该模式运行中还存在着相关指导老师配备不足，无法向全校本科生开展培养，监督机制不够完善，活动开展形式过于教条等方面的问题。点加团队还应继续创新和完善 “科研团队——小组二元育人模式”的制度，并在高等医学教育改革背景下实践和探索本科生科研素质培养模式，为地方和国家培养出具备优秀科研素质，符合应用创新型的人才。

为评估和分析其上部屋盖的风荷载及风致动力响应，在汕头大学风洞实验室进行刚性测压模型的风洞试验。模型的几何缩尺比为 1:200。试验中以原型地址120 m作为参考高度，以36 个风向角在模拟的B 类地貌湍流边界层来流条件中进行。确定计算结构风荷载的重现期采用100 a，对应的基本风压分别为0.60 kN/m2，风洞试验采样频率为312.5Hz。

3 基于Ritz-POD法求解大跨屋盖的风致动力响应

3.1 本征正交分解法(POD)

本征正交分解法(POD)可以有效地描述大跨屋盖结构表面风压分布特征，其具体作法为：将已知脉动风压向量{()}表示成另一空间状态[]，此状态使得{()}在{}上的投影值a()最大化。

其中：{}可通过求解脉动风压空间协方差矩阵的特征值获取，且满足均方值条件。

由于均方值反映了脉动风压向量{()}中与能量相关的信息，所以，可以使用本征值来衡量前几阶模态所包含的风荷载能量，只需根据少量的前几阶本征模态便可以较好地描述大跨屋盖表面脉动风压特征。其中，前阶本征模态对脉动风压贡献的模态累积率可定义如下：

一般认为当b大于0.75时，所取的本征模态数目即可满足要求。

3.2 基于荷载的Ritz模态分析

Ritz向量叠加法的一个关键问题是如何得到荷载的空间分布形式。对于大跨度屋盖的风致振动响应计算，通过荷载向量状态空间的POD转换，可以用较少的几组本征模态作为Ritz模态分析的初始荷载向量，得到基于风荷载POD分解的Ritz模态振型；运用较少的振型再通过谐波激励法[15]便可得到与运用较多传统自由振动振型分析法几乎相同的风致响应分析精度。

3.3 Ritz-POD法联合运用求解大跨屋盖结构的风致动力响应

综合运用POD和基于荷载的Ritz模态分析结果，采用随机振动相关理论，以SAP2000有限元软件的MATLAB应用程序编程接口环境(API)，编制大跨屋盖结构的风致动力响应相关分析程序，其基本流程见图2。

图2 Ritz-POD法计算屋盖风致响应计算流程图

4 Ritz-POD法和传统模态分解法求解大跨屋盖风致响应结果对比分析

以广州国际体育演艺中心的上部结构大跨度屋盖有限元模型为例，结合风洞测压实验得到的表面风荷载时程，用Ritz-POD法和传统模态分解法分别求解其风致动力响应。根据风洞测压实验的屋盖表面脉动风荷载分布状况， POD分析中各阶对应的模态累计贡献率如图3所示。从图3可见：前5阶的模态贡献率高达73.64%。因此，选取本征模态前5阶对应的本征模态向量，作为基于荷载的Ritz模态分析的初始向量组。在进行Ritz模态分析时，选用的Ritz模态阶数为前40阶，而传统模态分析时选取的振动模态阶数为前100阶。

图3 POD分解法各阶模态累积贡献率曲线

4.1 水平方向(方向)风致位移均方根相应对比分析

对按传统模态分解法和Ritz-POD法求得的上部屋盖模型，在风向角为0°及重现期为100 a时，求得的各节点水平方向(方向)风致位移均方根分布图分别见图4和图5。从图4和图5可见：2种方法中，均方根最大位移均对应有限元节点221号，Ritz-POD(Ritz)法对应的最大位移为0.000 170 m，传统模态分解法(Modal)对应的最大位移为0.000 163 m。从图5所示的由2种分析方法所得位移均方根相对误差可见，两者误差最大出现在有限元节点611号，为80.39%；二者误差最小比值出现在有限元节点294号，为−9.62%；而对于其他大部分节点，两者得到的风致位移响应均大致相同。从图4和图5可以看出：Ritz法仅需前40阶就可以得到与传统振型分解法取前100阶模态组合结果相同的准确性和精度。

图4 水平方向(X方向)风致位移均方根分布

图5 Modal与Ritz方法水平方向的风致位移均方根相对误差

4.2 竖直方向(方向)风致位移均方根相应对比分析

一般地，大跨度屋盖结构的最大风致位移出现在垂直方向上。图6所示为传统模态分解法和Ritz-POD这2种方法在0°风向角及100 a重现期条件下，求得的各节点竖直方向(方向)风致位移均方根分布图。图7所示为这2种方法计算的风致位移均方根相对误差图。从图6和图7可看出：Ritz-POD(Ritz)法对应的位移最大值为0.002 8 m，传统模态分解法的位移最大值为0.003 0 m。从图7可以看出：2种方法位移误差最小比值出现在有限元节点579号，其值约为−10%，而对于其他大部分节点，两者得到的风致位移响应值均大致相同。这再一次验证了用Ritz-POD法分析具有密集自振频率分布的大跨度屋盖风致响应是高效和有效的。

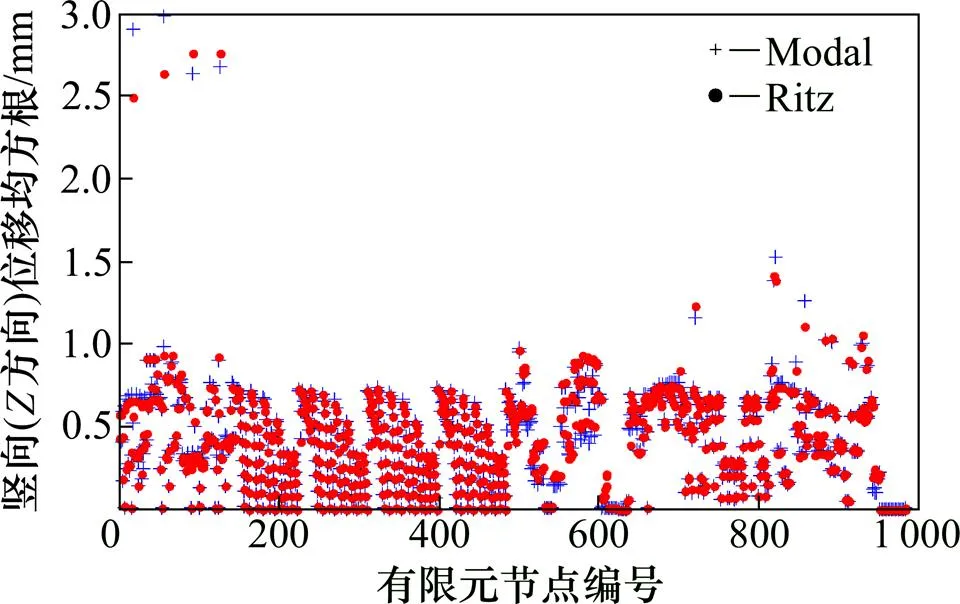
图6 竖直方向(Z方向)风致位移均方根分布

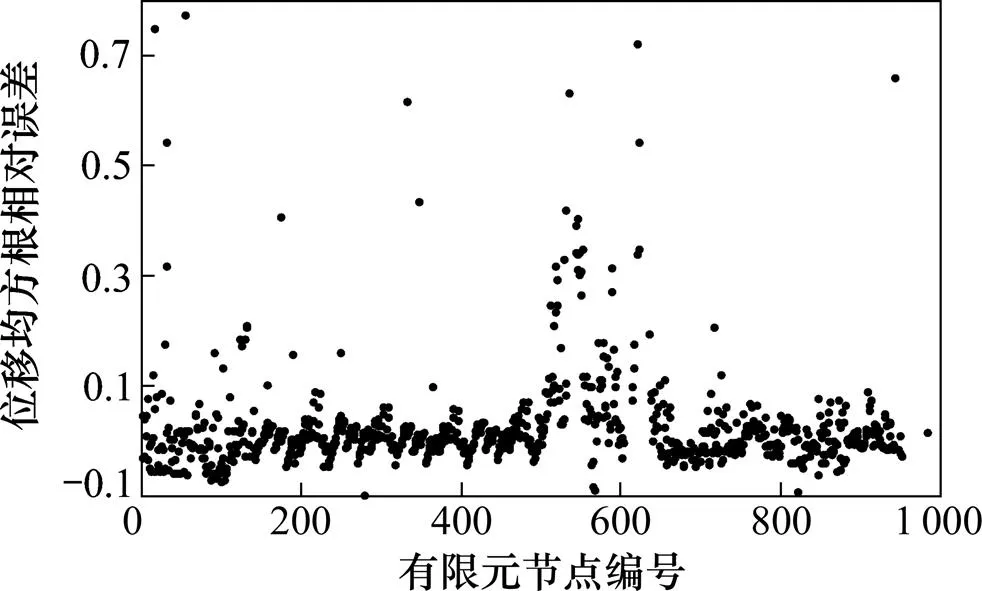
图7 Modal与Ritz方法竖直方向的风致位移均方根相对误差

5 考虑下部支撑结构共同作用的大跨屋盖结构风致动力响应分析

广州国际体育演艺中心体育馆的整体结构体系由刚度相对较小的上部大跨空间屋盖钢结构和具有较大刚度的下部混凝土结构支承体系共同组成，因此，下面采用2种不同的有限元分析模型进行风致响应对比分析：1) 将上部大跨钢屋盖和下部混凝土支撑结构全部加以考虑(此处称之为整体模型)，动力分析时所选取的模态为按传统自由振动分析得到的自由振动模态，模态阶数为32，其计算模型如图8所示；2) 图1(b)中仅考虑上部屋盖结构的有限元模型(此处称之为简化整体模型)，但其下部结构的影响用上、下部连接处的支撑刚度(如表1所示)进行模拟。动力分析时选用的模态采用基于Ritz-POD分析的振动模态，Ritz模态数目也采用32阶，以对比2种不同计算模式下钢结构屋盖的风致动力响应分析结果。

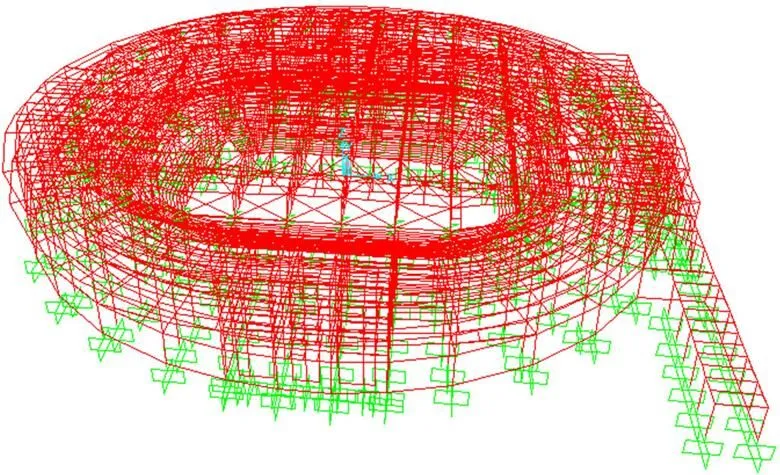
图8 考虑上、下部共同作用的整体结构有限元分析模型

整体有限元分析模型(见图8)前10阶自振频率及对应的振动特征见表2，考虑上、下部共同作用(见图1(b))的简化整体模型见表3。

表2 整体有限元分析模型的前10阶自振频率

表3 大跨屋盖结构考虑下部支承刚度的前10阶Ritz模态自振频率

5.1 2种计算模式在竖直方向(Z方向)风致位移均方根对比分析

采用2种不同的计算模型，在风向角为0°及重现期为100 a时，求得各节点竖直方向(方向)风致位移均方根分布及两者相对误差分别见图9和图10。其中，由于个别有限元节点位移远大于其余大多数节点位移，为避免在相同图形比例中将其余大多数节点位移的信息淹没，个别具有较大节点位移的响应结果未在图中显示(后续采用同样处理手法)。整体模型的最大竖向位移出现在有限元节点502号，其值为0.776 mm；简化整体模型的最大竖向位移出现在节点94号，其值为2.8 mm。从图9和图10可以看出：这2种计算模型的风致位移分布状况大致相同。由于简化整体模型采用的是基于脉动风荷载分布的Ritz模态，而整体模型的是常规自由振动模态，且这2种模型的模态数目均为32阶，因此，采用简化整体模型得到的绝大部分节点风致动力响应结果稍大，两者相对误差大部分集中在−2%~20%之间。

图9 2种计算模式下竖直方向(Z方向)风致位移响应

图10 整体模型与简化整体模型计算模式下的竖直方向(Z方向)风致位移均方根相对误差

5.2 2种计算模式在水平方向(方向)风致位移均方根相应对比分析

采用2种不同的计算模型，在风向角为0°及重现期为100 a时，求得各节点在水平方向(方向)风致位移均方根分布及相对误差分别见图11和图12。从图11和图12可见：整体模型的最大向位移出现在有限元节点145号，其值为0.224 mm；简化整体模型的最大向位移出现在有限元节点401号，其值为0.700 mm。从表2和表3可以看出：简化整体模型和整体模型的前10阶均以竖向振动模态为主，但在简化整体模型的前10阶中仍有部分水平侧向振动的模态出现，因此，这2种模型的水平风致位移响应的误差比竖向位移响应的强度大。从图12可以看到：两者相对误差大部分集中在20%~50%之间。

图11 2种计算模式下水平侧向方向(Y方向)的风致位移响应

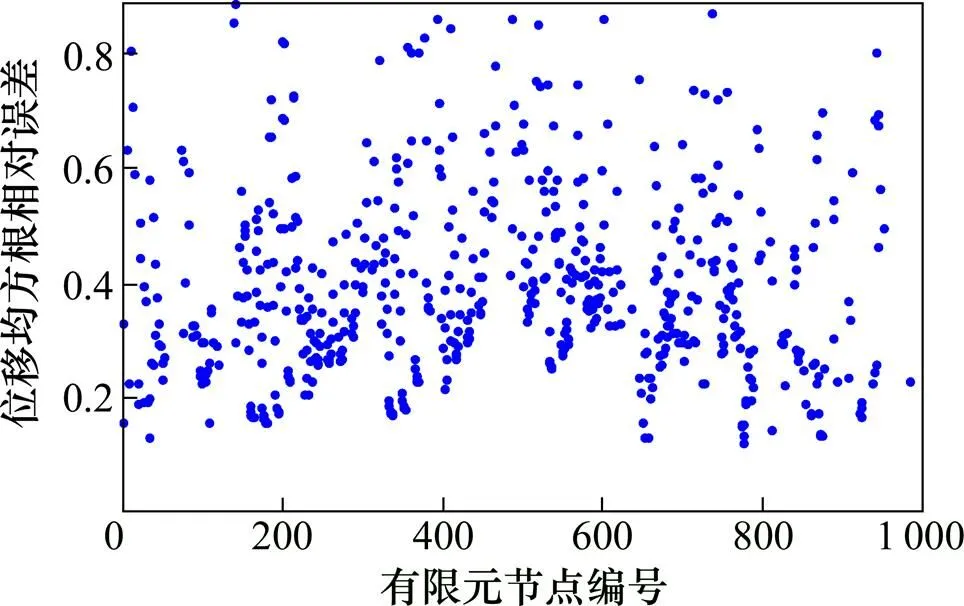
图12 整体模型与简化整体模型计算模式下的水平侧向方向(Y方向)的风致位移均方根相对误差

通过上述2种模型的风致动力响应分析结果可以看出：采用简化整体模型计算大跨度复杂屋盖结构的风致动力响应与采用整体模型相比，一方面，可以通过上、下部连接处的支承刚度有效地模拟这两者之间的共同作用，大大减少了有限元分析的工作量；另一方面，在风致动力响应分析中，当两者采用相同数目的参振模态时，简化整体模型所包含的对屋盖风致位移响应有直接贡献的模态比整体模型的多，因此，采用本文的简化整体模型，结合Ritz-POD模态分析方法，可以用相对较少数目的参振模态进行风致动力响应分析，得到的风致振动结果与用整体模型的分析结果相比略偏大。

6 结论

1) 采用本文的Ritz-POD方法，可以有效地将POD和基于荷载的Ritz模态求解方法有机地结合在一起，这为具有复杂表面脉动风荷载分布和具有密集耦联模态的大跨度空间屋盖结构的风致动力响应计算提供了一种高效简洁的方法。采用Ritz-POD法仅需前40阶，就可以得到与传统振型分解法取前100阶模态所得分析结果相同的准确性和精度。

2) 简化整体模型可以通过上、下部连接处的支承刚度，有效模拟其两者之间的共同作用。同时，结合Ritz-POD模态分析方法，简化整体模型还可以采用数量较少的Ritz模态，得到的风致振动结果与用整体模型的分析结果相比略偏大。

[1] Holmes J D. Wind loading of structures[M]. New York: Spon Press, 2001: 163−221.

[2] Yasui H, Marukawa H, Katagir J, et al. Study of wind-induced response of long-span structure[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1/2/3): 277−288.

[3] Holmes J D, Sankaran R, Kwok K C S, et al. Eigenvector modes of fluctuating pressures on low-rise building models[J]. J Wind Eng Ind Aerodyn, 1997, 69/70/71(7/8/9/10): 697−707.

[4] Tamura Y, Suganuma S, Kikuchi H, et al. Proper orthogonal decomposition of random wind pressure field[J]. Journal of Fluids and Structures, 1999, 13(7/8): 1069−1095.

[5] 倪振华, 江棹荣, 谢壮宁. 本征正交分解技术及其在预测屋盖风压场中的应用[J]. 振动工程学报, 2007, 20(1): 1−8. NI Zhenhua, JIANG Zhaorong, XIE Zhuangning. POD technique and its application for predicting wind pressure on roof[J]. Journal of Vibration Engineering, 2007, 20(1): 1−8.

[6] 江棹荣, 倪振华, 谢壮宁. POD 在大跨屋盖风致响应计算中的应用[J]. 土木工程学报, 2007, 40(6): 1−6. JIANG Zhaorong, NI Zhenhua, XIE Zhuangning. Application of POD in wind-induced response analysis of large span roof[J]. Journal of Civil Engineering, 2007, 40(6): 1−6.

[7] 李方慧, 倪振华, 沈世钊. 单层球面网壳结构风致响应计算的块里兹向量法[J]. 振动工程学报, 2007, 20(2): 128−132. LI Fanghui, NI Zhenhua, SHEN Shizhao. Block Ritz method for wind-induced response analysis of single-layer latticed domes[J]. Journal of Vibration Engineering, 2007, 20(2): 128−132.

[8] Wilson E L, Yuan M W, Dickens J M. Dynamic analysis by direct superposition of Ritz vectors[J]. Earthquake Engineering & Structural Dynamics, 1982, 10(6): 1648−1666.

[9] Gu J M, Ma Z D, Hulbert G M. A new load-dependent Ritz vector method for structural dynamics analysis: Quasi-static Ritz Vectors[J]. Finite Elements in Analysis and Design, 2000, 36(3/4): 261−278.

[10] 李方慧. 大跨屋盖结构实用抗风设计[M]. 哈尔滨: 黑龙江大学出版社, 2008: 32−48. LI Fanghui. The practical wind resistant design of large span roof structures[M]. Harbin: Heilongjiang University Press, 2008: 32−48.

[11] 武岳, 陈波, 沈世钊. 大跨度屋盖结构等效静风荷载研究[J]. 建筑科学与工程学报, 2005, 22(4): 27−31. WU Yue, CHEN Bo, SHEN Shizhao. Equivalent static wind loading analysis of large-span roof structures[J]. Journal of Architecture and Civil Engineering, 2005, 22(4): 27−31.

[12] Nakayama M, Sasaki Y, Masuda K. An efficient method for selection of vibration modes contributory to wind response on dome-like roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 73(1): 31−43.

[13] 胡继军, 李春祥, 黄金枝. 网壳风振响应主要贡献模态的识别及模态相关性影响分析[J]. 振动与冲击, 2001(1): 22−28.HU Jijun, LI Chunxiang, HUANG Jinzhi. The identification of dominated contribution vibration modes and modal correlation analysis for wind-induced vibration analysis of reticulated shells[J]. Vibration and Shock, 2001(1): 22−28.

[14] 张建胜, 武岳, 陈波, 等. Ritz-POD法及其在大跨度屋盖结构风振分析中的应用[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(6): 603−607.ZHANG Jiansheng, WU Yue, CHEN Bo, et al. A new load-dependent Ritz Vector method for wind-induced response analysis on large span roof structure[J]. Journal of Shenyang Architecture University (Natural Science), 2005, 21(6): 603−607.

(编辑 陈灿华)

Wind-induced response analysis of long-span roof structure with supporting stiffness

CHEN Zhiyong1, PENG Zhenbin1, CHEN Wei2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. Guangzhou Engineering Contractor Group Co. Ltd., Guangzhou 510030, China)

Based on the wind tunnel test data for the surface wind load of Guangzhou International Sport Complex (GISA), the wind-induced response analysis was conducted for the long-span roof steel structure by utilizing different analyzed models (practical and simplified models) and considering the supporting stiffness. Traditional natural vibration mode shapes and load-dependent Ritz mode shapes were utilized in the frequency domain analysis on the wind-induced response of the long-span roof structure. The initial load vectors for load-dependent Ritz mode analysis were selected from the first five eigenvectors in the POD (proper orthogonal decomposition) decomposition on the covariance matrix of fluctuated wind loads on the long-span roof. The results show that with the combined application of Ritz-POD method, the simplified roof structure model with less Ritz modal shapes obtains larger values in the wind-induced response than those obtained by the practical model does. The simplified model with Ritz-POD algorithm can be supplied as an effective method for the wind-induced response analysis on such complex roof structures.

long span roof structure; wind-induced response; Ritz vector; POD decomposition

10.11817/j.issn.1672-7207.2015.04.039

TU317.2；TU311.3

A

1672−7207(2015)04−1475−07

2014−05−12；

2014−07−22

国家自然科学基金资助项目(51378134)(Project (51378134) supported by the National Natural Science Foundation of China)

陈智勇，博士研究生，从事地质与结构工程研究；E-mail：kfqczy@163.com