基于强度折减的岩质边坡稳定性分析方法

2015-10-12张长龙

地球 2015年7期

关键词：滑面岩质步数

张长龙

（山东省地矿工程勘察院山东济南250014）

基于强度折减的岩质边坡稳定性分析方法

张长龙

（山东省地矿工程勘察院山东济南250014）

在众多岩质边坡稳定性分析方法中，基于强度折减的分析方法具有绝对优势，此方法不仅能反映出岩质边坡的应力场分布特征，而且还可以动态反映出边坡破坏过程，避免了其他方法需要过多假设的弊端，可直接得出稳定性安全系数进而确定危险滑面。

强度折减法岩质边坡稳定性

岩质边坡指山体表面因一定角度的倾斜，而形成的侧向临空面的岩体，岩体在自身重量及外界影响力的作用下，高处岩体具有向低处滑动的趋势。如果边坡岩体表面的滑动力超过岩体本身的抵抗力，将可能发生滑坡或崩塌。

1　基于强度折减的岩质边坡稳定性分析方法概述

基于强度折减的岩质边坡稳定性分析，指运用材料强度c、φ除以折减系数F，得到一组新的参数，并将其作为新的材料强度参数，通过折减系数F的不断增大或减少直至临界状态，从而得到最终的折减系数，此折减系数即为安全系数。其分析方程可以表述为：

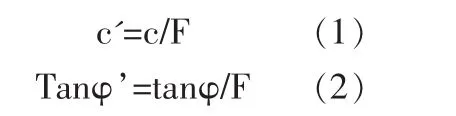
目前，国内对基于强度折减系数所进行的岩质边坡稳定性分析主要集中在三个方面的内容：（1）最危险滑面的数据分析；（2）边坡失稳临界点及判据的确定；（3）强度折减方式的选择。

2　基于强度折减的岩质边坡稳定性分析

2.1最危险滑面的数据分析方法

折减法在计算岩质边坡稳定安全性系数的过程中，通过位移等值线可以直观的观察到边坡中危险滑面所发生的破坏过程。在位移等值线图上的密集点可确定出易发生滑坡的危险位置，或连接等值线图上的最大幅值，确定连线中心并逐渐向两侧扩展，形成一个近似圆弧的区域，在该区域的中间位置，应变增量的数值最大，且自上而下贯通形成一个弧形曲线，该弧形曲线所表达的就是易发生滑坡的位置，即滑面位置。

2.2边坡失稳临界点及判据的确定

边坡失稳临界点是折减法分析岩质边坡稳定性的关键，也就是确定何时达到发生滑坡的临界值是非常重要的，这个过程直接取自于判据的确定。一个科学合理的临界判据能够使最终得到的安全系数更加具有说服力，也更加符合实际。当前常用的临界判据主要有三种：收敛性表现、塑性区贯通表现、特征点位移改变。多年的研究实践表明，当收敛性表现的计算迭代次数为500时为最佳，若超过这个临界值即可确定已发生边坡破坏性改变。在运用折减法计算边坡稳定性时，一般将边坡岩土体设定为理想塑性材料，岩土体受到破坏后进入塑性改变状态，发生位移，当整个岩土体都变发生塑性改变后，可认为边坡塑性区贯通且已发生破坏。特征点位移改变的理论基础是当边坡破坏达到临界值时，部分点的位移会随之发生流动改变，因此，可将其作为特征点进行边坡破坏临界判据。

2.3强度折减方式的选择

2.3.1整体折减方式

一般情况下所采用的强度折减计算方式都为整体折减方式，其应用原理是对所有材料强度均参照相同的折减系数进行统一计算，将计算所得的强度参数代入到公式中反复计算直至边坡失稳，以求得危险滑裂面。整体折减方式所采用的计算模型为三维边坡几何模型，如图1所示。该模型为六面体结构，假设岩质边坡条件为：四周边界法向约束，底部自下而上固定约束，模型最上部为自由区域。在对计算成果进行分析时，需将材料强度c、φ值同时除以折减系数F，反复多次，F值不断增大，且每次增量为0.01，直至计算不收敛。在不同折减系数的影响下，迭代步数也不同，迭代步数随折减系数的变化关系如表1所示。由统计表中可见，当折减系数由1.04变为1.05时，迭代步数激增突变，当折减系数为1.05时计算不收敛，从而将计算不收敛判据确定为边坡安全系数为1.05。

图1　三维边坡几何模型

表1　不同折减系数下的迭代步数统计表

2.3.2局部折减方式

为求得坡面某部分的安全系数，往往需要用到局部折减法。局部折减法的原理是不对整体折减法计算所得的滑面附近岩土体进行折减，而对其他部分岩土体强度参数进行折减，从而得到山体坡面某部分的安全系数。在局部折减模型中，不同折减系数下跌代步数的计算结果见表2。从统计表中的分析数据可以看出，当折减系数为1.47时，迭代步数发生激增突变，因此，在迭代步数准则下所得的边坡安全系数为1.46，以计算不收敛为边坡稳定性判据的条件下所得的安全系数为1.47。

表2　不同折减系数下的迭代步数统计表

3　强度折减分析方法在济南绕城高速公路南线K24段路线中的应用

3.1工程概况

济南绕城高速公路南线属山区高速公路，其中K24段路线边坡工程地质条件较为复杂，属于典型的灰岩边坡类型，在开发过程中曾数次发生较大规模的滑坡现象。经测定，滑坡岩土体主轴方向长度约为92m，平面呈簸箕形，陡壁高差约为11m。

3.2强度折减分析方法的实际应用

参照边坡设计规范中的相关规定，济南济南绕城高速公路南线K24段路线边坡所允许的最小安全系数见表3。制作计算模型时，需将坡面设定为自由边界，且需将模型底部设定为固定边界，在初始条件下只需考虑边坡岩土体自身应力的影响。根据工程实际情况模型，可进行特定高度的应力应变分析和边坡失稳性分析，从而确定特定高度下所应采取的边坡支护措施。