模糊-主成分分析综合评价法在地下水水质评价中的应用

2015-10-12杜军凯李晓星

中国环境监测 2015年4期

杜军凯，傅尧，李晓星

1．中国水利水电科学研究院，北京 100038

2．中国环境科学研究院，北京 100012

水质评价方法概括起来可分为单因子评价法及综合评价法。单因子评价法的基本思想是一票否决原则，即在所有参与评价的水质指标中，若有某一单项水质指标超标，则所属水域的使用功能便丧失或者得不到满足［1］。国内外众多科研工作者针对水质问题，在综合评价方面开展了诸多工作。①指数评价法:Horton等于1965年首次提出水质评价的指数体系，即豪顿水质指数［2］;Brown水质指数选取11种重要的水质参数［2］，根据专家的意见进行加权处理;普拉特水质指数将各参数换算的污染指数相加［3］，求其算术平均值;姚裴［4］提出了分指数分级评分迭加法;谢宏斌［5］提出了分指数合成计算环境质量综合指数的方法。②模糊评价法:郑成德［6］提出环境质量评价模糊集理论，将模糊模式识别应用于环境质量评价中;孙蕾［7］应用模糊数学中模糊聚类的最大矩阵元法和模糊相关分析法对水质进行分析、聚类和评价;何玉冰［8］将模糊贴近度法、模糊距离法及模糊综合评判与加权平均复合模型应用于水质模型中。③灰色评价法:张松滨等［9］提出了共斜率灰色贴近度分析法并将其应用于水环境质量评价之中;史晓新等［10］在灰色关联度的基础上，构造了一种新的水环境质量评价灰色模式识别模型;吴雅琴［11］把水环境视为灰色系统采用灰色关联分析方法进行水质评价。

目前地下水水质评价实际工作中，多采用《地下水环境质量标准》(GB/T 14848—1993)给出的单项组分评价法及综合评价法。单项组分法简单直观，但水体使用功能是否受损，与水质指标的影响程度有关，不应该简单地认为一项水质指标超标，则水体一定不满足使用功能［12］;综合评价法为每个水质等级对应设置了固定的权重，采用评分法以其加权值得到综合得分作为划分水质等级的依据，但由于不同区域地下水补、排条件，污染物组成情况，污染物组分运移方式等相差迥异，固定的权重并不适宜作为水质评价工作中的统一参数。

立足科研及实践需求，地下水水质评价亟需一种更为科学、合理的评价方法。针对地下水水质评价因子多、影响因素复杂、综合评价难的特点，该文选取主成分分析法与模糊数学法作为基本数学方法，建立了模糊-主成分分析综合评价法的地下水水质耦合评价模型，并将其应用于辽宁思山岭铁矿地下水水质评价中。

1 评价模型的建立

1.1 主成分分析法

主成分分析是利用降维的思想，在损失很少原始信息的前提下把多个指标转化为几个综合指标的多元统计方法。通常把转化生成的综合指标称之为主成分，其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，这就使得主成分比原始变量具有某些更优越的性能。在研究复杂问题时就可以只考虑少数几个主成分而不至于损失太多信息，从而更容易抓住主要矛盾，揭示事物内部变量之间的规律性，同时使问题得到简化，提高分析效率［13］。

主成分分析法采用降低数据维度的方式，将多种影响水质的因子简化为几个综合因子以反映水体水质状况，在水质评价因子选取中获得广泛的应用［14-17］。该法的优势在于保留了所有原始因子的信息，但对水体综合水质状况无法做出直接表达。

1.2 模糊综合评价法

模糊综合评价［18］以模糊数学为基础，应用模糊关系合成原理，将一些边界不清、不宜定量的因素定量化，运用模糊数学法中的隶属度描述评价等级，确定各污染因子的权重，进而评价水质类别。

模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法，该方法已被广泛用于各种类型水体水质的综合评价中［19-23］。但该方法在评价因子选取上存在较强的主观性:若参与评价的因子过多，权重太小，会造成模糊矩阵信息丢失过多，出现评价结果趋于均化、不易分辨的现象。《地下水环境质量标准》中有分类标准的因子共39项，如何适当选取评价因子，对评价成果的质量有直接影响。

1.3 模糊-主成分分析综合评价模型

基于以上对2种数学模型的分析，将主成分分析与模糊综合评价结合起来，融合2种方法的优势，取长补短，以达到“强强联合”的目的。建模的基本思想:因子选取上采用主成分分析法，选出影响地下水水质的主要因子;水质评价采用模糊综合评价法，将提取的主成分作为模糊综合评价模型的输入，建立模糊-主成分分析综合评价法的地下水水质耦合评价模型。

评价模型的技术路线图如图1所示。

1.3.1 数据标准化

为了排除数量级和量纲不同带来的影响，需对原始数据进行标准化处理，标准化公式:

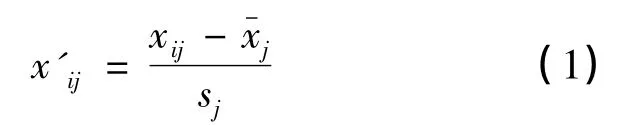
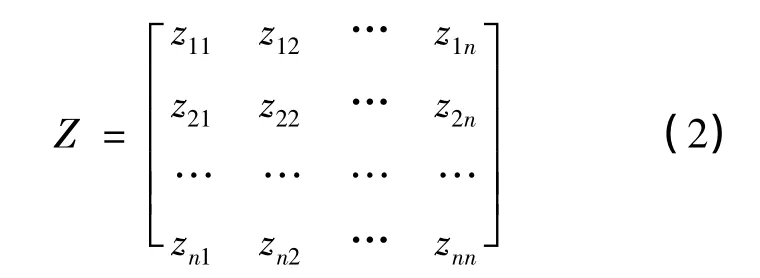
1.3.2 相关系数矩阵的计算

式中R为n阶的对称矩阵。

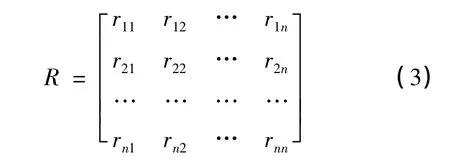
rij(i，j=1，2，…，n)为原变量 xi与 xj的相关系数，rij=rji，其计算公式:

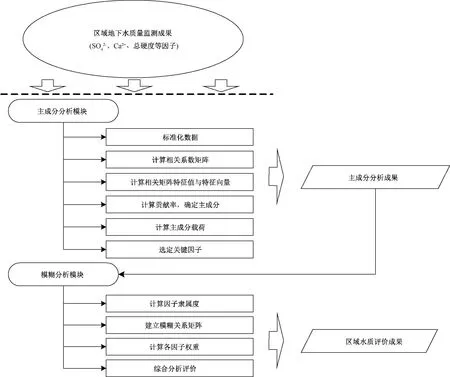
图1 评价模型技术路线图

1.3.3 计算相关系数矩阵R的特征值与特征向量

求R的特征值 λi(i=1，2，…，n)及其对应的特征向量 ui(i=1，2，…，n)，且 λ1≥λ2… ≥λn。其中λi为主成分Fi的方差，方差越大，对总方差的贡献越大。

要求 ‖ui‖ =1，即，其中uij表示向量ui的第j个分量。

1.3.4 计算贡献率并确定主成分

1.3.5 计算主成分载荷

特征向量ui与主成分荷载lij的关系:

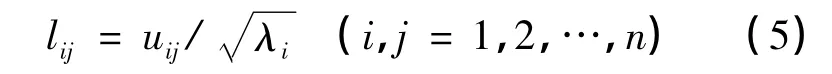
1.3.6 主成分因子分析

对选定的m个主成分，根据主成分载荷值选取每个主成分的主要控制因子，组成累积方差贡献率大于或等于85%的前m个主成分的r个因子［10］，作为模糊综合评价的评价因子。

1.3.7 隶属度函数

隶属度函数可用式(6)～式(8)表达。

第Ⅰ类水体的隶属度函数(j=1):

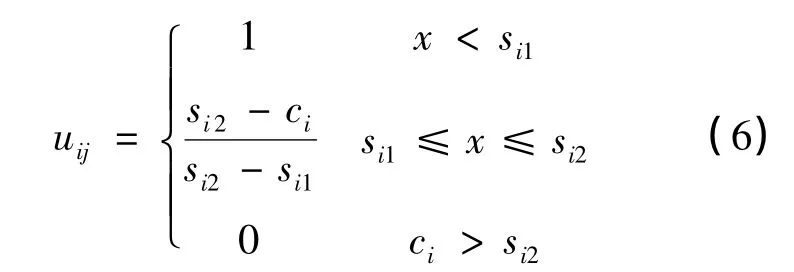
第j类水体的隶属度函数(j=2、3、4分别代表第Ⅱ、第Ⅲ、第Ⅳ):

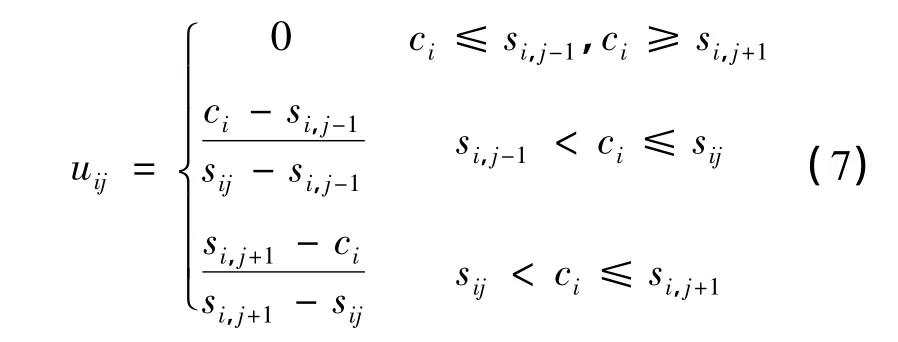
第Ⅴ类水体的隶属度函数(j=5):

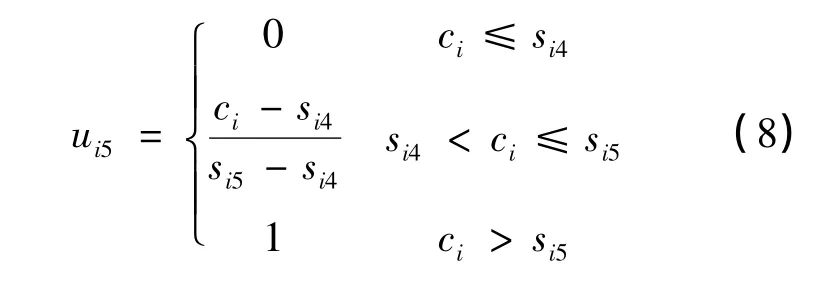
式中:ci为第i种污染物实测浓度值(i=1，2，…，m)，mg/L;si为第i种污染物j级水质标准(j=1，2，…，5)，mg/L。

1.3.8 建立模糊关系矩阵

通过计算m项参数对5级水质标准的隶属度，可得到一个m×5阶单项污染程度隶属度矩阵R。

矩阵的行表示参评因子对5个级别水质的隶属程度;列表示参评的各单项指标对某一级水质的隶属程度。

1.3.9 计算权重

各因子的权重，采用式(10)进行计算:

式中:Ci为第i种污染物的实测值;Si为《地下水质量标准》(GB/T 14848—1993)中Ⅲ类水质的标准值。

在实际计算中，利用式(5)计算出来的权重值可能大于1，但模糊数学运算仅允许在［0，1］区间连续取值，因而需对各单项权重进行归一化

处理:

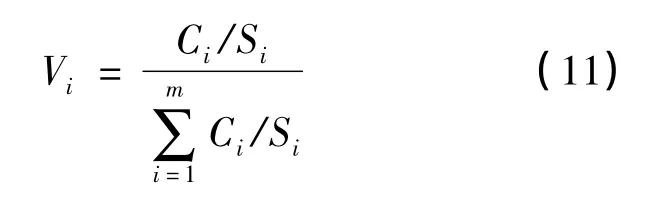
然后将归一化结果列成1×m阶行矩阵，输入A=(V1，V2，V3，… ，Vm)。

1.3.10 综合评价

通过复合运算来实现模糊综合评价，得出评价结果 B=A·R。

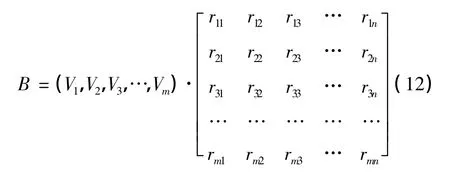
为了进行综合评价，运算时采用“取小取大法则”［24-26］进行，即类似矩阵乘法，相乘取其中小者为“积”;相加取其中大者为“和”;从而求得输出B，它是一个1×n阶行矩阵。最后根据矩阵中的数值大小，将最大数值所在的序次确定为水质等级。

2 实例

思山岭铁矿位于辽宁省本溪市东南郊16 km，区域含水层主要有松散层孔隙含水层、碎屑岩孔隙裂隙含水层、碳酸盐岩溶隙裂隙含水层、基岩风化裂隙含水层。在矿区评价范围内共布置10个地下水水质现状监测点。矿区范围内地下水水质执行《地下水质量标准》(GB/T 14848—1993)中Ⅲ类水质的标准。

选取10个地下水的水质现状监测点的8个监测因子作为评价依据，详见表1。

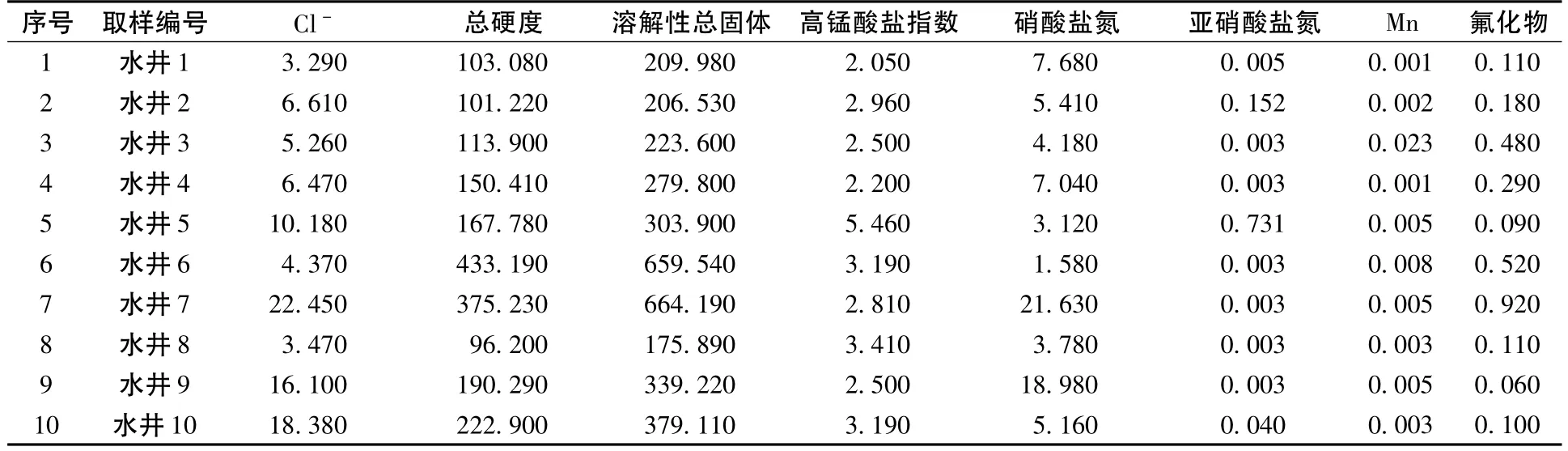
表1 矿区地下水井监测数据表

首先对10个监测断面的8个指标数据进行标准化处理。根据标准化数据计算其对应的相关系数矩阵。

根据相关系数矩阵计算其特征值，并计算主成分贡献率和累积贡献率，见表2。

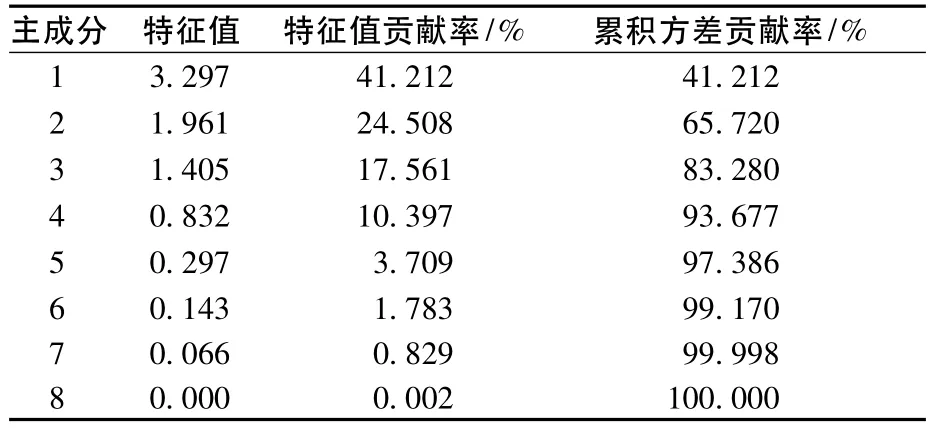
表2 特征值和主成分贡献率及累积贡献率

前3个主成分的特征值贡献率累积方差率达到了83.3%，说明这3个主成分已经能够反映原始指标所提供的绝大部分信息，所以确定主成分个数为3个。

计算初始因子载荷矩阵，每一个载荷量表示主成分与对应变量的相关系数，初始因子荷载矩阵见表3。

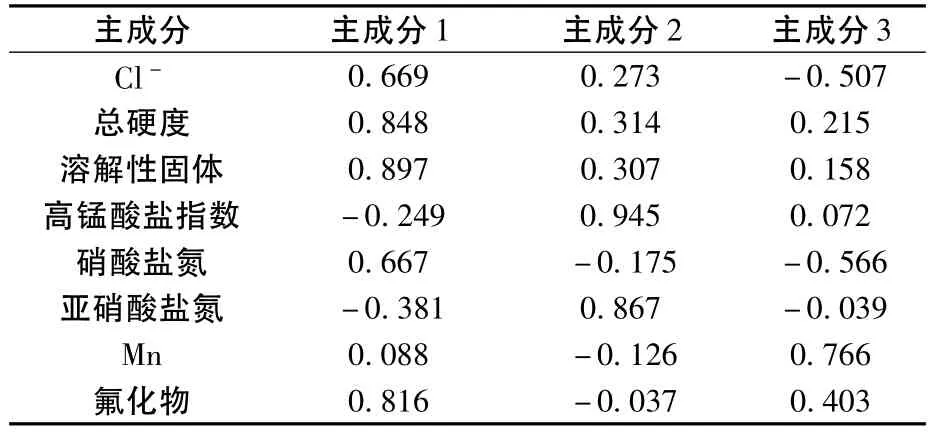
表3 初始因子荷载矩阵

每个污染指标初始因子荷载系数表示与主成分的相关程度，正值表示正相关，负值表示负相关，绝对值越接近1，表示相关程度越高。

用初始因子载荷矩阵中的数据除以主成分相对应的特征值求平方根，得到2个主成分中每个指标所对应的系数，才能得到相应的主成分载荷值，主成分荷载值见表4。

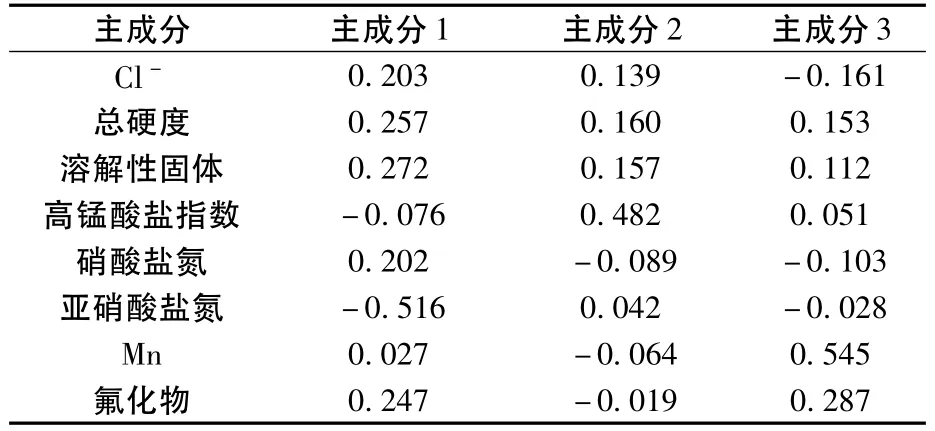
表4 主成分荷载值

从主成分载荷值大小来看，与第一主成分密切相关的是亚硝酸盐氮;与第二主成分密切相关的是高锰酸盐指数;与第三主成分密切相关的是Mn。

因此，采用主成分分析法为下阶段模糊综合评价法选取的主要因子为亚硝酸盐氮、高锰酸盐指数和Mn等。

建立模糊关系矩阵。以水井1为例进行计算，根据各评价因子的隶属度函数及其实测值，求出各评价因子对于各级水质标准的隶属度，并组成模糊矩阵R。

建立评价因子的权重矩阵A。水井1各评价因子的权重计算方法和结果如表5所示。

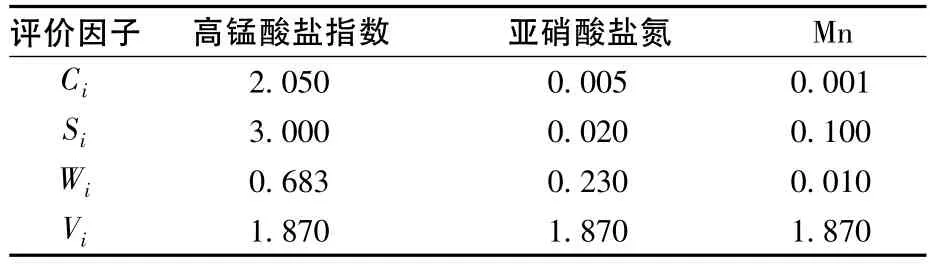
表5 各评价因子权重

模糊综合评价。以水井1为例，根据模糊综合评价法的原理，A=(0.366，0.123，0.005)，B=A·R，计算综合评价结果。

计算结果表明，水井1的水质属于Ⅰ类水的可能性为12.3%，属于Ⅱ类水的可能性为12.3%，属于Ⅲ类水的可能性为36.6%。根据最大隶属度原则，即哪一级水质的隶属度最大，则水质污染就是哪一级。则水井1的水质评价等级为Ⅲ类。

同理得出其他水井水质的各级隶属度及水质评价结果，见表6。

根据前文分析，该区域的地下水水质受污染状况如表6所示，所选10口样井中，共8口井水质优于Ⅲ类，2口井水质劣Ⅴ类。

与单因子评价法相比，该模型计算成果与之在总体趋势上保持高度的一致性，具体情况有所不同。所选10口样井中，4口井水质评价结果相同，6口井评价结果有差异，本文所得模糊-主成分综合评价成果均比单因子评价成果高一个水质等级。由此可见，模糊-主成分综合评价法既有较高的精度，又有效地降低了数据分析工作量，一定程度上解决了在水质评价工作中“满足精度”与“精简工作量”之间的矛盾。

3 结论

1)矿区地下水水质评价是一个多因素、多指标的复杂系统，靠单一指标或固定权重的模式来评价水资源的污染程度具有片面性。模糊-主成分分析综合评价法在保留研究对象原始因子信息的前提下，将原有水质因子进行简化，避免参与模糊综合评价的因子过多，对模糊综合评价的结论产生影响;同时模糊综合评价考虑了不同的评价指标对地下水水质的影响权重，评价结果更精确、合理、可信。

2)将建立的模型应用于辽宁思山岭铁矿矿区地下水现状评价中，评价结果表明，矿区地下水已不同程度受到了污染。这主要是由于矿区附近的居民农业生产和生活污水排放，农机具的加工、维修、清洗和使用造成区域地下水水质超标，与实际情况相符。

3)考虑到区域水资源禀赋条件的差异，大力推广水循环处理设施、有效利用中水资源，提高水资源综合利用效率是缺水地区水资源开发利用的必由之路。该模型综合考虑了选取评价因子的合理性及其对地下水水质的影响权重，尤其适用于多因素、多指标的复杂系统的水质评价工作。

［1］夏青，陈艳卿，刘宪兵．水质基准与水质标准［M］．北京:中国标准出版社，2004．

［2］郑英铭．对水利部门作水质评价的某些看法［J］．水文，1984(3):31-34．

［3］薛巧英．水环境质量评价方法的比较分析［J］．环境保护科学，2004，30(4):64-67．

［4］姚斐．分指数分级评分叠加法在水质评价中的应用［J］．干旱环境监测，1998，12(2):83-84．

［5］谢宏斌．环境质量评价与预测方法的现状［J］．四川环境，1998，17(3):37-40．

［6］郑成德．环境质量评价模糊集理论与模式研究［J］．四川环境，1997，16(4):64-68．

［7］孙蕾．模糊数学评价河流水质的模型探讨［J］．贵州环保科技，2000，6(4):24-28．

［8］何玉冰．模糊聚类法及相似优先比在河流水质评价中的应用［J］．河南大学学报:自然科学版，1997，27(2):21-25．

［9］张松滨，李万海，王红．环境质量评价中的灰色贴近度分析［J］．环境保护科学，1998，24(6):37-39．

［10］史晓新，夏军．水环境质量评价灰色模式识别模型及应用［J］．中国环境科学，1997，17(2):127-130．