降雨及爆破振动条件下岩质边坡稳定性研究

赵奎， 余乐兴， 邵海， 何文， 吴冰， 程三建

(1.江西理工大学资源与环境工程学院，江西 赣州341000;2.中国地质环境监测院，北京100081; 3.厦门紫金工程设计有限公司，福建 厦门 361000;)

降雨及爆破振动条件下岩质边坡稳定性研究

赵奎1， 余乐兴1， 邵海2， 何文1， 吴冰3， 程三建1

(1.江西理工大学资源与环境工程学院，江西 赣州341000;2.中国地质环境监测院，北京100081; 3.厦门紫金工程设计有限公司，福建 厦门 361000;)

文章采用Geostudio软件中的Quake/w模块和Slope/w模块对边坡进行了爆破稳定性研究，在Quake/w模块中加入了爆破振动速度时程曲线和降雨后实测的边坡水位线作为数值计算的两种边界条件，并将动态响应结果导入Slope/w模块中，应用有限元极限平衡法计算爆破振动时边坡的安全系数，以此分析考虑水时边坡在爆破振动影响下的稳定性.同时，为研究水位线对计算结果的影响，分别将有水位线、无水位线及自重应力场下三者的计算结果进行了对比分析.研究表明，与纯自重应力场作用下的边坡稳定性相比，爆破振动下的安全系数降低了6.88%，爆破振动与地下水联合作用下的安全系数降低了24%，地下水对边坡稳定性有非常明显的影响.

爆破振动;地下水;降雨;边坡稳定性

0 前 言

边坡稳定性问题的研究是露天矿的重要课题之一.自1927年美国人Rockwell首次发表有关爆破振动响应的文章以来[1]，众多学者在爆破振动对边坡稳定性影响研究方面做了大量工作，随着计算机技术的发展以及多学科之间的交叉，数值模拟等越来越多的手段运用到此项研究中来.潘东[2]引入降振技术，通过LS—DYNA有限元分析程序，结合福建某矿山的工程实际对其进行数值模拟，分析了边坡受中深孔爆破影响后的稳定性状况.胡志强等[3]以歪头山铁矿为研究对象，对该矿爆破产生的地震波的传播过程以及地震波的衰减规律进行研究，分析了爆破振动对边坡的影响大小，提出了减震爆破措施，起到了有效保护边坡的作用.王建国等[4]利用FLAC3D软件将现场所实测的爆破数据在丽江阿海电站左岸高陡边坡三维模型的底部输入，分析了边坡体内部速度、位移以及应力等变量的分布规律，从而对该边坡在爆破载荷作用下的稳定进行判断.郭鲁川等[5]以鄂尔多斯丰胜奎露天煤矿边坡作为研究对象，运用灰色关联理论，分析了影响爆破振动的各因素，从中选出影响爆破振速的最优因素，通过研究药量、距离、孔数与爆破振动之间的关系，指导实际安全生产，提高边坡稳定性.陈建平等[6]运用强度折减法分析边坡稳定性.对于岩质边坡而言，其稳定性受多种因素相互影响，从单一角度对其进行分析往往得到的结果是片面的.通过分析以上研究现状得知:在传统的边坡爆破振动分析中，大多并未考虑地下水对计算结果的影响.由于岩体赋存条件复杂，而地下水是地质体赋存重要条件之一，它对岩体力学性质影响较大[7-11].在降雨过程中，由于雨水的物理化学作用和力学作用将削弱岩体的强度，因此分析边坡在降雨时的稳定性是非常必要的.在以往岩质边坡稳定性问题的研究中，分析爆破振动对边坡稳定性影响时往往忽略了地下水的作用.通过此次的研究，为边坡在地下水和爆破振动联合影响下的稳定性分析提供思路，具有重要的理论价值，并为相关问题的解决提供一定科学依据和借鉴.

以银山铅锌矿露采坑东北边坡为研究背景，现北东边坡180 m标高以上已靠帮，露天采场最终境界边坡最高达到420 m，边坡属超高边坡.边坡岩体工程地质特性复杂，边坡在扩帮过程中特别是在北东边坡局部已发生了滑坡、崩落、塌陷等较为严重的地质灾害，研究其降雨条件下爆破振动对边坡稳定性的影响意义重大.

1 工程地质、水文地质概况

1.1 工程地质

岩石是构成岩质边坡的主要结构，其岩性、物理力学性质将直接影响岩质边坡的稳定性.对东北边坡进行钻探取样，钻探中发现主要岩性为千枚岩，岩芯总采取率为96.71%，总RQD值为90.67%，依次可见地表土、灰白色绢云母化千枚岩、灰黑色绢云母化千枚岩、灰黄色绢云母化千枚岩、灰白色绢云母化千枚岩、灰黑色绢云母化千枚岩、灰黄色绢云母化千枚岩、灰白色绢云母化千枚岩.同时部分区域还夹杂着英安斑岩、石英斑岩等.各类岩石的力学参数，见表1.

表1 各类型岩石的力学参数

1.2 水文地质

矿区气候属亚热带湿润性气候区，四季更替分明，因受海洋性气候影响，春夏多雨，秋冬干燥，据数据统计，年平均降雨量2185.4 mm，蒸发量为1198.95 mm，最大年降雨量2870.4 mm，昼夜最大降雨量达311.7 mm，雨季集中于春季和夏初，全年降雨天数150～192天，平均为171天.矿区内无水库、湖泊等较大地表水体，仅有一条自北东向南西流淌的银山小河，河谷宽50～100 m，河床宽2～6 m.

根据矿区水文地质情况分析，矿区水文地质条件较为简单.矿区为一个独立的水文地质单元，由较为坚硬的岩石组成，岩石几乎不含水，相对隔水层赋存在没有受断裂影响的地段;基岩风化带与构造裂隙含水带单位涌水量较小，属弱富水性含水层;第四系孔隙含水层分布不连续，没有形成整层的规模，也属于弱富水性含水层.通过分析矿区水文地质情况可知大气降水是本文所研究的北东边坡地下水的主要补给途径.

2 模型设计及参数选取

2.1 模型设计

根据银山矿岩性分布三维立体图，在最高的北东边坡上截取一个剖面，模型边界范围的大小对有限元计算精度的影响较大，根据有关资料统计，当坡脚到左端边界的距离设为边坡高度的1.5倍，坡顶到右端边界的距离设为边坡高度的2.5倍，且上下边界的总高不低于2倍的坡高时，能够得到较为理想的计算精度，故根据此建立边坡剖面，如图1.

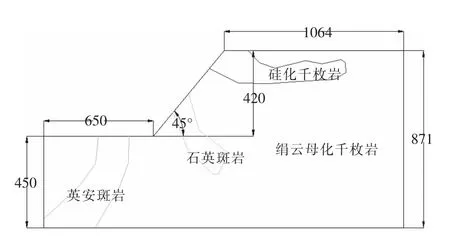
图1 45°边坡剖面模型尺寸示意图/m

模型根据银山北东边坡为研究对象进行建立，实际边坡最终边坡角为45°，采用平面应变三节点及四节点单元对模型离散，边坡剖面模型得到3788个节点(Nodes)、3779个单元(Elements)，如图2.

图2 东北边坡45°剖面数值计算模型

2.2 参数选择

爆破振动对边坡稳定性的影响属于动力学研究，数值分析仍以银山北东边坡作为研究主体，岩体力学参数选取见表1，假设岩体各向均质同性.在动力学的数值分析中，模型网格尺寸的选取和设置必须要能确保足够精确的波传播，Kuhlemeyer和Lysmer提出在数值计算时，由最高频率所组成的输入波波长应当大于所用网格单元尺寸的8～10倍[12-13].本模型输入的动载荷主频为30 Hz，参考相关文献[14]，网格尺寸选为10 m.

在爆破工程中，所用药量单耗及震源距离边坡的位置的不同将对结果产生重要影响.通常计算爆破岩体质点振动速度v的经验公式为:

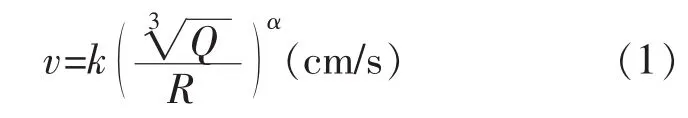
式(1)中:Q是一次爆破的炸药量，kg;R是测点与震源中心的距离，m;k是与岩体性质、地质条件有关的系数;α是爆破地震波衰减系数.根据研究成果文献[15]通过对银山爆破振动的数据进行回归分析，并对公式(1)进行了修正，修正过后的公式为:

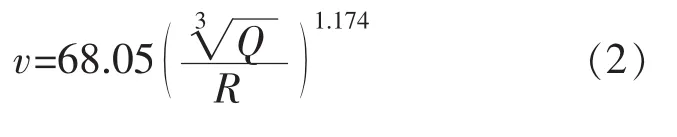
采用动力学Quake/W模块进行计算时主要考虑P波(方向垂直于边坡剖面)和SV波(方向平行于边坡剖面)的共同作用对边坡的影响.通过现场对爆破振动数据采集，得到了计算边坡剖面处的爆破速度时程曲线，见图3.

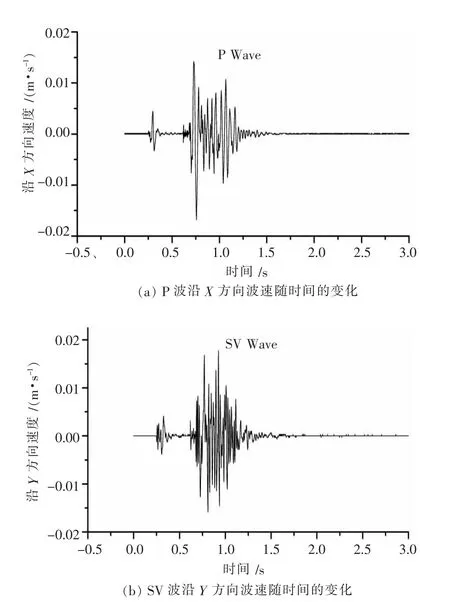
图3 边坡剖面测点的振动速度时程曲线

图4 测点与爆源的位置图

此振动波形通过BlastMateⅢ型测振仪于银山矿露天开挖爆破时采集，测点与爆源的位置见图4，单段最大药量为8000 kg，爆源在96 m平台，测点在122 m平台，测点距离爆源水平距离145 m，高差26 m，直线距离147.2 m.

3 边界设定

爆破动载荷必须由于考虑了P波(方向垂直于边坡剖面)和SV波(方向平行于边坡剖面)共同作用对边坡的影响，此次数值计算模型下边和两侧采用粘滞边界.同时，在边坡面中加入爆破振动速度时程曲线，在边坡内部增加边坡实测水位线.其中降雨后的水位线通过实地测量获取资料.

在计算模型整个边坡面施加爆破振动测得的速度时程曲线时，由于该边坡属超高边坡，距离对振速的影响较大，因此，考虑将边坡面分成8段(见图5)，根据分别计算各段的振速作为爆破振动边界条件，以减小边界条件带来的误差.

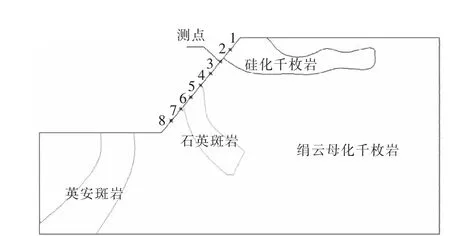
图5 边界条件载入分段示意图

根据修正的萨道夫斯基公式(2)，以及分段中点距爆源的直线距离，可计算得到每一段的合成速度值，见表2.并可得到相对测点合成速度的比值，再将各比值乘以测点的波速，最终可得到各分段的振动速度时程曲线，此时得出的8段速度时程曲线便可分段加载到边坡面以模拟爆破振动边界条件.

表2 各分段最大振速与测点最大振速比值

将降雨后实测的水位线与各分段的振动速度时程曲线两类边界条件加入边坡模型，确定了边坡剖面计算模型，见图6.

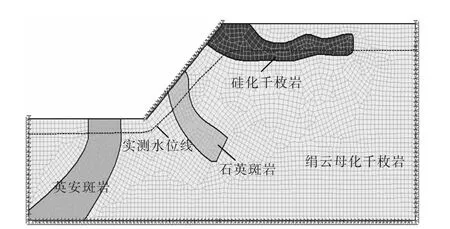
图6 加入实测水位线时的计算模型

此次计算，根据不同条件，需要计算三种工况下边坡稳定性，如表3.

表3 工况分类

4 计算结果及分析

4.1 工况一

当Quake/w动力学模块完成边坡振动计算后，将计算结果导入Geostudio软件的Slope/w模块，采用Newmark Deformation方法计算出边坡在爆破振动作用下的永久位移，用有限元极限平衡法计算爆破振动时的安全系数，以此分析边坡稳定性情况，结果见图7～图12.

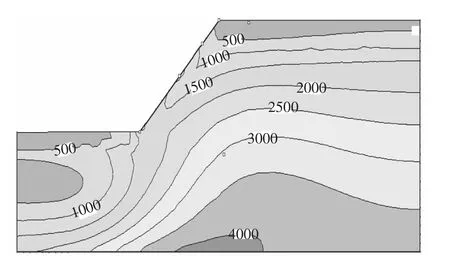
图7 剪应力云图/kPa

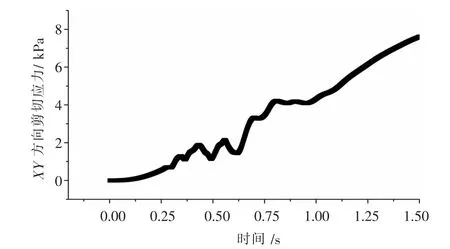
图8 坡脚历史点剪应力随时间的变化

由图7～图8可知，在爆破振动的影响下，坡脚处剪应力总体随时间逐渐增大，并从坡顶至坡脚，剪应力逐渐增大，有从坡脚剪出的趋势.

图9 位移云图/m

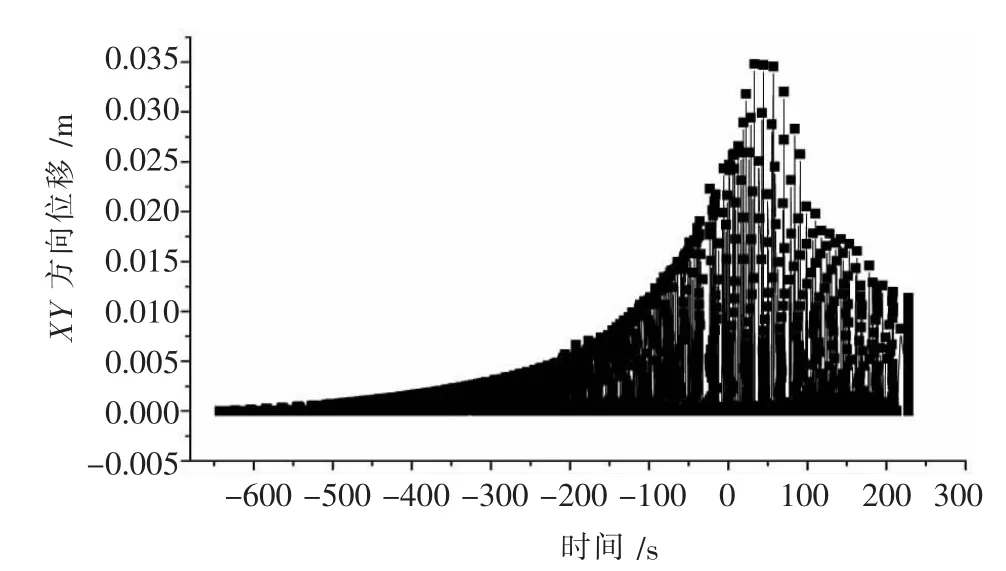
图10 爆破振动1.5 s时边坡标高与节点位移图

由图9～图10可知，距离爆源最近的中部位移量相对较大，位移最大处达34.8 mm，坡脚处位移量为3.2 mm.

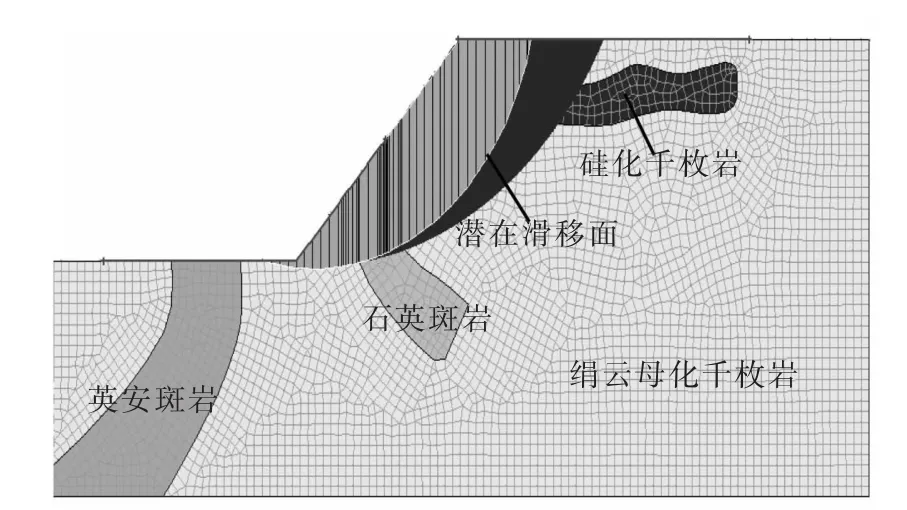
图11 边坡潜在滑移面云图

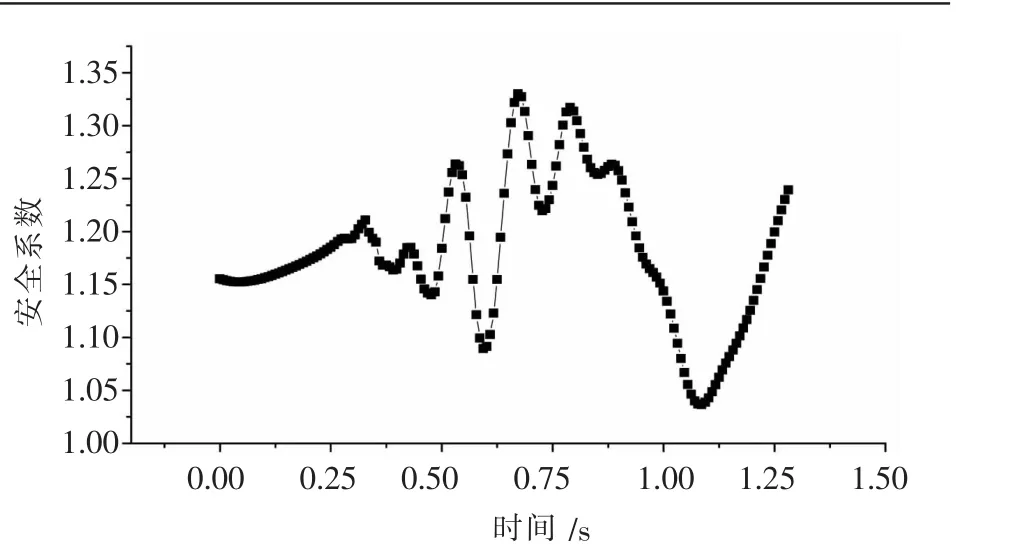
图12 边坡安全系数随时间的变化

由图11～图12可知，在考虑地下水和爆破振动联合影响下，由爆破引起边坡振动的过程中，边坡的安全系数的最小值为1.024，根据《滑坡防治工程勘察规范》(DZ/T 0218-2006)，计算所得的安全系数低于1.05的基本稳定值，因此考虑水时边坡在爆破振动过程中是欠稳定的.

4.2 工况二

在爆破边界不变，不加水位线的条件下，计算模型见图13.

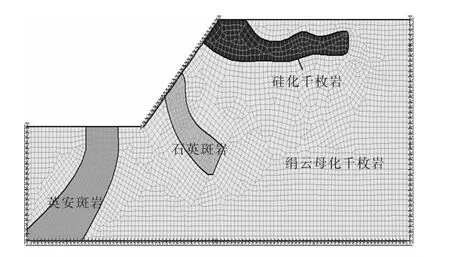
图13 加边界条件后的计算模型

由计算结果可知，未添加水位线时，爆破引起边坡振动的过程中，边坡的安全系数的最小值为1.257.

4.3 工况三

在此边界条件下，只考虑自重应力，见图14，先通过Geostudio软件中的Quake/w模块，选择I nitial Static方法进行自重应力场的计算，然后将结果带入Slope/w模块，进行边坡安全系数的计算.

由计算结果可知，自重应力场下计算得到的边坡安全系数为1.350.

根据本章对不同边界条件下的边坡稳定性数值分析，得到相应边界条件下的边坡最小安全系数，见表4.

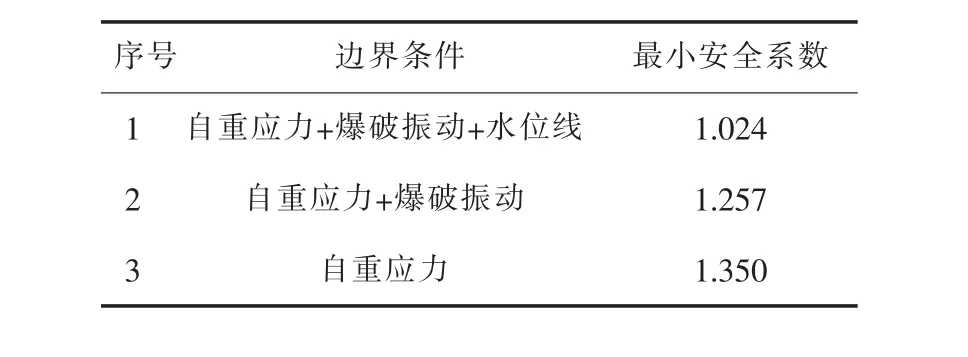
表4 不同边界条件下的边坡最小安全系数

通过表4可知，当只考虑自重应力的情况边坡最小安全系数为1.350，考虑自重应力与爆破振动时边坡最小安全系数为1.257，考虑自重应力、爆破振动和水位的情况边坡最小安全系数减小到1.024.通过有无水位线时爆破振动下的边坡最小安全系数与只考虑自重应力场时的最小安全系数对比可知，爆破振动使边坡的安全系数降低了6.88%，爆破振动与地下水的联合作用使边坡的安全系数降低了24%.

5 结 论

在爆破振动测试及现场水位监测的基础上，运用Geostudio岩土软件进行边坡的稳定性数值计算，以爆破振动的P波 (方向垂直于边坡剖面)和SV波(方向平行于边坡剖面)作为边界条件施加在二维边坡剖面上，同时在模型中添加了实测水位线，研究了考虑地下水时边坡在爆破振动影响下的稳定性.通过研究主要得到如下结论.

1)由数值计算结果可知，考虑地下水和爆破振动联合作用的边坡安全系数随时间呈波动变化，边坡最小安全系数为1.024，此时边坡为欠稳定状态.坡脚的剪应力随爆破振动时间逐渐增大，坡体有从坡脚剪出的潜在可能.

2)分析对比了不同边界条件下的边坡最小安全系数，当只考虑自重应时边坡最小安全系数为1.350，考虑自重应力与爆破振动时边坡最小安全系数为1.257，考虑自重应力、爆破振动和水位的时边坡最小安全系数减小到1.024.

3)与自重应力场所得安全系数相比，爆破振动使边坡的安全系数降低了6.88%，爆破振动与地下水的联合作用使边坡的安全系数降低了24%.因此在分析爆破振动对边坡稳定性的影响时，地下水对边坡稳定性的影响重大.

[1]曾志林.爆破振动对高陡边坡稳定性影响及控制技术研究[D].长沙:中南大学，2010.

[2]潘东.露天矿山中深孔爆破边坡稳定性影响研究[J].山西建筑，2012，38(20):72-74.

[3]胡志强，李永强，张杰，等.爆破震动对露天边坡稳定性影响研究[J].矿业快报，2007，458(6):49-51.

[4]王建国，栾龙发，张智宇，等.爆破震动对高陡边坡稳定性影响的数值模拟研究[J].爆破，2012，29(3):119-122.

[5]郭鲁川，费志超，王莹.露天矿爆破震动效果与参数的灰色关联分析[J].现代矿业，2013，529(5):170-171.

[6]陈建平.边坡强度折减法判据及点安全系数研究及工程应用[D].赣州:江西理工大学，2012.

[7]孙广忠，孙毅.岩体力学原理[M].北京:科学出版社，2011.

[8]饶运章.岩土边坡稳定性分析[M].长沙:中南大学出版社，2012.

[9]祝玉学，张绪珍，王国中.露天矿边坡优化设计方法[J].岩土工程学报，1989，11(3):11-20.

[10]冯锦艳，王金安，蔡美峰.露天高陡边坡角优化设计及稳定性分析[J].中国矿业，2005，14(4):45-48.

[11]赵奎，王明，何文，等.露采爆破振动对拟建水库坝体影响研究[J].金属矿山，2013，448(10):130-133，139.

[12]Hoek E，Brown E T.Underground excavations in rock[M]. London:Institution of Mining and Metallurgy，1980.

[13]袁文军，阮怀宁，孔不凡，等.广义H-B准则中经验参数的改进取值方法[J].人民黄河，2013，35(4):98-100.

[14]徐曾和.渗流的流固藕合问题及应用[D].沈阳:东北大学，1998.

[15]郭峰.关于爆破地震波波速计算方法的探讨[J].爆破，1987 (3):22-27.

Research on rock slope stability in the condition of rainfall or blasting vibration

ZHAO Kui1，YU Lexing1，SHAO Hai2，HE Wen1，WU Bing2，CHENG Sanjian1
(1.School of Resource and Environment Engineering，Jiangxi University of Science and Technology，Ganzhou 341000，China;2.China Institue of
Geological Enviromental Monitoring，Beijing 10081，China;3.Xiamen Zijin Engineering Design Co.Ltd，Xiamen 361000，China)

This paper studies the influence of blasting vibration on the slope stability by using Quake/w module and Slope/w module of Geostudio software，as two kinds of boundary conditions for numerical calculation.The velocity time history curve of blasting vibration and slope water line measured after rainfall are added to the Quake/w module，and results of dynamic response are imported into the Quake/w module，with the limit equilibrium method used to compute the safety factor of slope blasting vibration.Then，the stability of the slope containing water is analyzed in the influence of blasting vibration.Meanwhile，in order to study the effect of water level on results，the three results that contain water line or not and under self-weight stress field are compared and analyzed.Research shows that compared with the safety factor of slope stability under pure gravity stress field，it reduced by 6.88%under the blasting vibration，and 24%under the joint action of blasting vibration and groundwater.Thus groundwater had obvious influence on the slope stability.

blasting vibration;groundwater;rainfall;slope stability

2095-3046(2015)01-0043-06

10.13265/j.cnki.jxlgdxxb.2015.01.008

O 382+.2

A

2014-09-09

江西省科技支撑计划项目(20141BBG70097);江西理工大学研究生创新专项资金项目(YC2013-X02)

赵奎(1969- )，男，博士，教授，主要从事岩土工程等方面的研究，E-mail:Yglmf_zk@163.com.