联合InSAR和水准数据的矿区动态沉降规律分析
2015-10-11杨泽发朱建军李志伟汪长城汪云甲陈国良
杨泽发,朱建军,李志伟,汪长城,汪云甲,陈国良
联合InSAR和水准数据的矿区动态沉降规律分析
杨泽发1,朱建军1,李志伟1,汪长城1,汪云甲2,陈国良2
(1. 中南大学地球科学与信息物理学院,湖南长沙,410083;2. 中国矿业大学江苏省资源环境信息工程重点实验室,江苏徐州,221116)
针对传统矿区动态沉降测量中特征点缺失导致沉降规律不可靠问题,提出基于新型合成孔径雷达干涉测量(interferometric synthetic aperture radar, InSAR)与传统水准技术观测的矿区地表沉降值,使用Logistic时间函数和Levenberg-Marquard (LM) 算法拟合分析矿区动态沉降规律以及其与地下开采的关系。研究结果表明:联合InSAR和水准测量沉降值拟合的动态沉降函数、加速度函数的均方差比仅利用水准的均方差分别提高89.0%和97.9%;Logistic时间函数能够较好地描述矿区地表单点的动态沉降过程,且各点的最大沉降速度和加速度极值发生时间与开采至该点的时间之间呈线性关系。
InSAR;水准;矿区动态沉降;Logistic时间函数
地下开采导致的变形预计和分析是开采沉陷研究的重要内容,也是评估其潜在地质灾害的重要依据。然而,传统的开采沉陷预计模型仅能估计地表稳定后的沉降和变形,忽略了开采过程中地表动态形变和破坏[1],因此,研究矿区地表动态沉降规律对矿山开采损害评估及地表建构筑物防护有重要意义。目前,矿区动态沉降规律研究主要基于传统的水准沉降数据[2]。由于该技术成本较高,其获取的沉降数据时间分辨率通常不高,致使地表动态沉降过程拐点即“特征点”可能未被测量(即“特征点缺失”),从而导致分析的动态沉降规律不可靠甚至错误[2−3]。近年来,合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)技术不断发展,其以低成本、全天候、全天时、高精度等优点在矿区地表沉降监测中得到广泛应 用[4−6]。然而,由于当前可用SAR卫星均为重复轨道飞行,其固定的重访周期也可能使InSAR数据未能监测动态沉降过程的特征点。考虑到单一InSAR或水准监测数据均可能出现特征点缺失,且两者在时间上通常不同步,因此,若联合传统的水准与新型的InSAR监测的沉降,则将大大提高地表沉降数据的时间分辨率,增加多余观测数,从而有效地降低单一数据源特征点缺失对动态沉降规律分析造成的不可靠程度。为此,本文作者提出联合InSAR和水准监测沉降分析矿区地表动态规律。首先,利用模拟数据分析特征点缺失对拟合结果精度的影响,研究联合InSAR和水准与仅利用水准监测沉降拟合的矿区地表沉降规律的差异。之后,基于钱营孜矿区水准与InSAR沉降测量值,使用Levenberg−Marquard(LM) 算法拟合Logistic时间函数的待估参数,并对比分析联合InSAR和水准与仅利用水准数据拟合结果的差异,最后分析地表动态沉降过程特征点出现时间与地下开采之间的关系,以便为矿区合理制定地表监测方案及建筑物保护措施提供参考依据。
1 矿区地表单点的动态沉降过程与Logistic时间函数
1.1 矿区地表单点的动态沉降过程
矿区地表单点沉降是一个复杂的时空过程,大致可分为3个时期:初始沉降期、主要沉降期和残余沉降期[7],如图1所示。目前,研究矿区地表动态移动规律的主要方法为时间函数法,具体有Knothe时间函 数[8−9]、双参数时间函数[10]、广义时间函数[11]、“S”型增长时间函数[12−13]等。其中:Knothe时间函数的一阶导数(沉降速度)、二阶导数(沉降加速度)与矿区实际沉降过程的对应值不符[13],因此,其结果精度不高;双参数时间函数和广义时间函数待估参数较多,其实际应用受到制约;“S”型增长时间函数由于更加符合矿区地表沉降的3个时期[13],因而被广泛研究和使用。在矿区地表单点动态沉降过程中存在3个重要特征点,即最大沉降速度点(见图1中点2)、最大和最小加速度点(见图1中点1和3),其不仅是约束沉降曲线形状的关键点,而且是评估地表建构筑物破坏持续时间及最大破坏强度出现时间的主要依据。因此,研究矿区地表动态沉降规律、分析其特征点与地下开采的关系有重要意义。
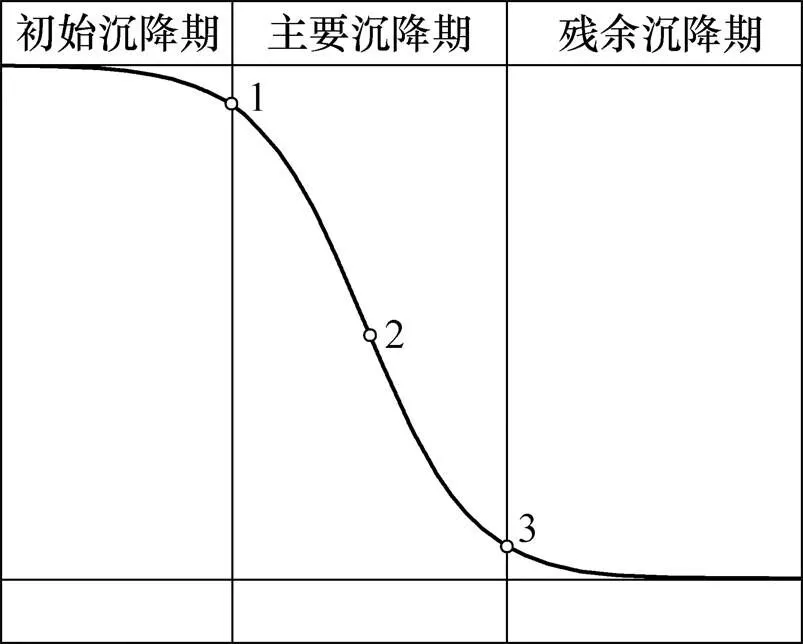
图1 矿区地表沉降过程的3个阶段
1.2 Logistic时间函数
Logistic时间函数为典型的“S”型增长曲线[13],其基本形式为
式中:()为地表在时刻的沉降值;0为地表最大沉降值;和为Logistic时间函数的形状参数。0,和为函数的待估参数。
由式(1)分别对时间求一阶、二阶导数,得到沉降速度()和加速度()表达式:
由于Logistic时间函数为典型的“S”型增长曲线,其也存在与矿区单点动态沉降过程相似的3个特征点,即最大沉降速度点和2个加速度极值点。3个特征点中任意1个点缺失均会导致拟合的Logistic函数存在 误差。
2 特征点缺失对Logistic时间函数拟合的影响
为了验证沉降监测中特征点缺失对Logistic时间函数拟合的影响,首先假定式(1)中0=−1 m,=1 200,=0.08,=0~300 d,并利用式(1)计算模拟的动态沉降曲线,如图2中曲线1所示。之后,假设该点有6组地表沉降测量数据,其监测周期分别为15,35,46,60,80和95 d(如图2(a)~2(f)中圆圈点所示),且首次观测时间均为第1天。为了使模拟的监测数据符合实际情况,在每组监测的沉降值中加入3 cm正态随机误差。随后,基于含误差的6组监测数据,利用LM算法分别估计6组Logistic时间函数的待估参数(即0,和),其拟合结果如图2中曲线2所示。

监测周期/d:(a) 15;(b) 35;(c) 46;(d) 60;(e) 80;(f) 95
为了更清晰地显示6组数据中监测时间与沉降过程特征点的分布关系,利用上述拟合的Logistic时间函数待估参数并按照式(3)分别计算6组对应的动态沉降加速度。图3所示为模拟沉降加速度曲线(由0=−1 m,=1 200,=0.08,代入式(3)计算结果,如图3中曲线1所示)与6组沉降加速度曲线(如图3中曲线2所示)对比结果。

监测周期/d:(a) 15;(b) 35;(c) 46;(d) 60;(e) 80;(f) 95
为了定量比较不同周期的监测数据对Logistic函数拟合结果的影响,计算模拟和拟合的动态沉降曲线之间的均方差(mean square error,MSE),其结果如表1所示。
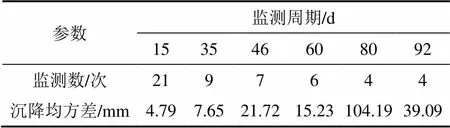
表1 模拟与拟合沉降曲线均方差
从表1可以看出:由于监测周期为15 d(如图2(a)所示)和35 d(如图2(b)所示)的监测时间基本覆盖了动态沉降曲线的特征点,其拟合曲线与模拟曲线吻合较好且精度相当(均方差分别为4.79 mm和7.65 mm)。然而,因为多余观测量减少,监测周期为46 d(如图2(c)所示)和60 d(如图2(d)所示)的拟合曲线均方差(分别为21.72 mm和15.23 mm)均大于15 d和35 d的结果。此外,虽然监测周期分别为80 d(如图2(e)所示)和92 d(如图2(f)所示)的观测次数均为4次,但后者更接近沉降过程的特征点,因此,其均方差明显低于前者(分别为104.19 mm和39.09 mm)。另外,从表1 还可发现:监测周期为15和35 d的观测次数(分别为21和9次)相差1倍多,但其拟合结果的精度却非常接近(其均方差之差仅为2.86 mm),其原因主要为后者的监测时间几乎覆盖了动态沉降曲线的所有特征点。
以上实验表明:矿区地表沉降监测时间是否覆盖该过程的特征点对拟合函数精度有较大影响,监测时间间隔太大,多余观测不足,且易缺失特征点,使得拟合的函数精度较低。因此,联合多源监测数据不仅能够增加函数拟合的多余观测量,同时增大了覆盖动态沉降过程特征点的可能性,从而有效提高矿区地表动态沉降规律的可靠性。
3 联合InSAR和水准数据的矿区沉降规律分析方法
鉴于传统InSAR技术监测的地表形变为雷达视线(line of sight, LOS)方向,且矿区变形主要以沉降为 主[1],因此,忽略水平移动分量对LOS向形变的贡献,直接将InSAR形变LOS转换为沉降值,即=LOS/cos(式中,为雷达传感器的入射角)。联合InSAR和水准数据分析矿区地表沉降规律的方法流程如下。
2) 合并InSAR与水准的监测结果,得到合并后的监测时间和沉降监测数据:
(5)
3) 从式(1)可以看出Logistic时间函数为含有指数的非线性函数,直接求解较复杂,因此,本文基于联合的InSAR和水准沉降数据,使用LM非线性算法拟合Logistic时间函数的待估参数0,和。求出各观测点的待估参数后,即可利用式(2)和(3)计算该点的沉降速度与加速度。
4) 估计所有监测点最大沉降速度、极大和极小加速度(3个特征点)的出现时间与地下开采经过该点的时间,分析地下开采与地表动态沉降特征点之间的关系函数,以便为合理地制定矿区变形监测方案以及地表建构筑物防护提供参考依据。
4 模拟数据验证
为了验证联合InSAR和水准沉降监测数据的优势和可靠性,假定第2节中监测周期为46 d的沉降值为InSAR监测值(图4中三角形),同时将之前拟合结果精度最低的一组数据(监测周期为80 d)设定为水准监测值(图4中圆圈点)。之后,按照第3节中描述的方法拟合Logistic时间函数的待估参数,并利用拟合的参数计算沉降加速度曲线,其结果如图4所示。

(a) 动态沉降曲线;(b) 加速度曲线
从图4可以看出:联合InSAR和水准监测数据拟合的动态沉降曲线(图4(a)中曲线2)、加速度曲线(图4(b)中曲线2)与对应的模拟曲线(图4(a)、4(b)中曲线1)较吻合,其均方差分别为和,而仅利用水准测量拟合(见图2(e)和3(e))的均方差分别为和。与后者相比,联合InSAR和水准测量数据的均方差分别提高了92.68 mm和2.431 mm/d2,其提高比例(即)分别为89.0%和97.9%。另外,相对于仅利用InSAR监测数据拟合的沉降曲线(图2(c))和加速度曲线(图3(c))的均方差21.72 mm和0.147 mm/d2,其精度也提高了47.8%和64.6%。实验结果表明:联合InSAR和水准监测数据后,多余观测量大大增加,其拟合结果的精度比仅利用InSAR或水准有大幅度提升,从而说明联合InSAR和水准分析矿区动态沉降规律比两者单独使用更可靠。
5 钱营孜矿区地表动态沉降规律
5.1 钱营孜矿区InSAR监测
选取4景覆盖安徽钱营孜矿区的ALOS PALSAR数据(幅号为660,轨道号为449),并将时间相邻的两景影像组成干涉对,其干涉参数如表2所示。为了将所有影像统一到同一空间坐标系,将所有SAR影像与2010−02−28获取的影像配准,然后对每个干涉对分别利用传统的“二轨法”(two-pass)获取矿区地表LOS向形变。其中,利用3弧秒shuttle radar topography mission (SRTM) digital elevation model (DEM)去除干涉对中的地形相位,使用改进的Goldstein滤波[14]对干涉图滤波。由于矿区范围较小,且大气扰动在1 km左右的距离内是相关的[15],因此,大气扰动引起的误差可以忽略不计。此外,由于轨道误差和大气相位长波部分在干涉图中通常以线性趋势呈现[16−17],因此,可利用多项式拟合削弱其对形变结果的影响。最后,利用最小费用流法解缠差分干涉图并将相位转换为LOS向形变值,得到3个时间段内的LOS向差分形变。为了获得矿区累计LOS向形变,将干涉对中相干性均高于0.3的点的形变值累加,然后忽略水平移动贡献而直接将LOS向形变转换为沉降值。

表2 干涉对参数
5.2 钱营孜矿区地表动态沉降估计
钱营孜矿区地表布设有一条走向观测线,在地下工作面开采期间共进行了10次观测(观测时间如图6圆圈点所示)。为了减少内插引入的误差,选取同时有水准和InSAR监测数据的6个观测点(如图5所示),分析该矿区地表动态沉降规律。之后,按照第3节中描述的方法分别获得仅利用水准与联合InSAR和水准监测数据拟合的Logistic函数待估参数,其结果分别如图6中曲线1和2所示。
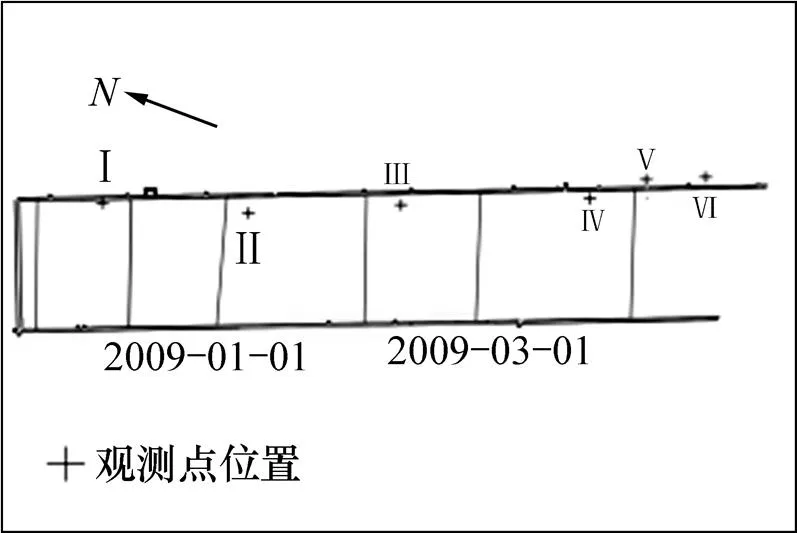
2009−01−01和2009−03−01为观测日期
从图6可以看出:无论对于水准数据或联合InSAR和水准数据,Logistic时间函数均能较好地拟合监测数据。此外,图6中点I~III(图6(a)~(c))由于水准测量几乎没有缺失沉降特征点,所以,联合InSAR和水准与仅利用水准数据拟合的曲线差异不大。而对于点Ⅳ~Ⅵ(图6(d)~(f)),仅基于水准测量数据拟合的动态沉降曲线相对于联合InSAR和水准测量值的结果均出现了主要沉降期时间增长、起始和终止沉降时刻滞后、最大沉降速度减小等问题。其主要原因是水准数据在主要沉降期(见图1)缺少观测值,从而无法约束该过程。若仅利用水准数据拟合的规律评估地表动态破坏和潜在地质灾害,容易使结果偏小,从而增加地表建构筑物的潜在危险。

观测点(见图5):(a) I;(b) II;(c) III;(d) IV;(e) V;(f) VI
1—仅利用水准拟合的Logistic曲线;2—联合InSAR与水准数据拟合的Logistic曲线;
○—水准监测数据;△—InSAR监测数据
图6 2009−11−19水准测量数据与联合InSAR和水准测量数据拟合6个观测点的沉降曲线
Fig. 6 Fitted Logistic curves of six observation points based on leveling measurements and integration of InSAR and leveling measurements
对于联合InSAR和水准监测值后的点Ⅳ~Ⅵ(图6(d)~(f)曲线2),由于增加了2010−05−31的InSAR监测数据,其对Logistic函数的整体形状起到了较好的约束作用(特别是对主要沉降期),因此,联合InSAR和水准数据比仅利用水准得出的规律更可靠。实验结果表明:Logistic模型能够较好地描述矿区地表动态沉降过程,而联合InSAR和水准数据分析矿区动态沉降规律由于增加了额外的监测时间和观测值,其结果比仅利用水准拟合结果可靠。
5.3 钱营孜矿区地下开采与地表动态沉降的关系
在矿区地表动态沉降过程中,最大沉降速度出现的时间是地表变形最迅速的时间,此时,地表建构筑物破坏最剧烈;而沉降加速度的2个极值点不仅是沉降从初始沉降到加速沉降、从加速沉降进入残余沉降的2个重要时间点,也是地表建构筑物经历潜在风险的起始和结束时间点。因此,研究地下开采与最大沉降速度、加速度极值出现时间的关系,对于提前制定地表建筑物防护措施和地表监测方案具有重要意义。
为了分析该矿区不同监测点的动态沉降过程特征点与开采进度的关系,首先分别计算该工作面(如图5)所示)推进至6个观测点时的时间1。随后,基于联合InSAR和水准数据拟合的Logistic模型待估参数,利用式(2)和(3)估计6个监测点的最大沉降速度发生时间2、加速度极大值、加速度极小值发生时间3和4,其结果如表3所示。最后,分别拟合1与2以及3和4之间的关系,其结果如图7所示。

表3 开采至观测点、最大沉降速度及加速度极值出现时间

(a) 最大沉降速度出现时间(T2);(b) 加速度曲线极大值出现时间(T3);(c) 加速度曲线极小值出现时间(T4)
从图7可以看出:开采至观测点的时间(1)与最大沉降速度出现时间(2)(如图7(a)所示)、与加速度2个极值点出现时间(3和4)(分别如图7(b)和7(c)所示)均呈线性函数关系,其相关系数为0.92~0.99。根据上述关系和地下工作面开采进度即可提前估计出地表建构筑物破坏持续时间(3到4时间段)、最剧烈的时间(2),合理地对建构筑物采取变形防护措施和有效地制定地表监测方案。
6 结论
1) 鉴于单一数据源易导致动态沉降过程特征点缺失,从而降低沉降规律的可靠性问题,提出了联合InSAR和水准监测数据分析矿区地表动态沉降规律的方法。首先通过模拟数据研究了特征点缺失对Logistic时间函数拟合精度的影响,分析得出联合InSAR和水准比仅用水准数据拟合的沉降规律更可靠。
2) 监测数据是否覆盖动态沉降过程对拟合结果有较大影响,而联合InSAR和水准监测数据拟合的Logistic时间函数、加速度函数的均方差相对于仅利用水准数据的均方差分别提高了89.0%和97.9%。
3) Logistic时间函数能较好地描述了矿区地表动态沉降过程,地下开采至观测点的时间与最大速度、加速度极值发生时间之间满足线性函数关系。该关系将地下开采与地表动态沉降的特征点联系起来,可为更好地制定地表监测方案、确定合理的地表建构筑物防护措施提供参考依据。
[1] Kratzsch H. Mining subsidence engineering[M]. Berlin: Springer, 1983: 1−20.
[2] Karmis M, Agioutantis Z. Enhancing mine subsidence prediction and control methodologies for long-term landscape stability[M]. United States, OSMRE: Pittsburgh Center, 2009: 12−31.
[3] 阎跃观, 戴华阳, GE Linlin, 等. DInSAR动态沉降监测错失点问题研究[J]. 煤炭学报, 2012, 37(12): 2038−2042. YAN Yueguan, DAI Huayang, GE Linlin, et al. Problem of dynamic of monitoring subsidence feature points missed by DInSAR technology[J]. Journal of China Coal Society, 2012, 37(12): 2038−2042.
[4] Jiang L M, Lin H, Ma J W, et al. Potential of small-baseline SAR interferometry for monitoring land subsidence related to underground coal fires: Wuda (Northern China) case study[J]. Remote Sensing of Environment, 2011, 115: 257−268.
[5] 尹宏杰, 朱建军, 李志伟, 等. 基于SBAS的矿区形变监测研究[J]. 测绘学报, 2011, 41(1): 52−58.YIN Hongjie, ZHU Jianjun, LI Zhiwei, et al. Ground subsidence monitoring in mining area using DInSAR SBAS algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 41(1): 52−58.
[6] Miguel C, Andrew J, Hooper R. Surface deformation induced by water influx in the abandoned coal mines in Limburg, the Netherlands observed by satellite radar interferometry[J]. Journal Applied Geophysics, 2013, 88: 1−11.
[7] Knothe S. Time influence on a formation of a subsidence surface[J]. Archiwum Gornicwai HuticwaKrakow, 1952, 1(1): 1−3.
[8] Lbrahim D, Yasuhiro M, Hiro L. GIS-Based computational method simulating the components of 3D dynamic ground subsidence during the process of undermining[J]. International Journal of Geomechanics, 2012, 12: 43−53.
[9] Kwinta A, Hejmanowski R, Sroka A. A time function analysis used for the prediction of rock mass subsidence[C]//Proceeding of the International Symposium on Mining Science and Technology. Xuzhou, China, 1996: 419−421.
[10] Komalski A. Surface subsidence and rate of its increments based on measurements and theory[J]. Archives of Mining Science, 2001, 46(4): 391−406.
[11] 王正帅, 邓喀中. 采动区地表动态沉降预测的Richards模型[J]. 岩土力学, 2011, 32(6): 1664−1668.WANG Zhengshuai, DENG Kazhong. Richards model of surface dynamic subsidence prediction in mining area[J]. Rock and Soil Mechanics, 2011, 32(6): 1664−1668.
[12] 张文志, 邹友峰, 任筱芳. Logistic模型在开采沉陷单点预测中的研究[J]. 采矿与安全工程学报, 2009, 26(4): 486−489. ZHANG Wenzhi, ZOU Youfeng, REN Xiaofang. Research on logistic model in forecasting subsidence single-point during mining[J]. Journal of Mining & Safety Engineering, 2009, 26(4): 486−489.
[13] Li Z W, Ding X L, Zheng D W, et al. Least squares-based filter for remote sensing image noise reduction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(7): 2044−2049.
[14] LI Zhiwei, DING Xiaoli, CHEN Dawei, et al. Assessment of atmospheric effects on repeat-pass insar measurements in southern China region[J]. Journal of Geospatial Engineering, 2005, 7(1): 1−10.
[15] Tarayre H, Massonnet D. Atmosphereic propagation heterogenetities revealed by ERS-1 interferometry[J]. Geophysical Research Letters, 1996, 23(9): 989−992.
[16] LI Zhiwei, DING Xiaoli, HUANG Chen, et al. Modeling of atmospheric effects on InSAR measurements by incorporating terrain elevation information[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2006, 68(1): 1189−1194.
Analysis of law of kinematic mining subsidence by integrating InSAR and leveling measurements
YANG Zefa1, ZHU Jianjun1, LI Zhiwei1, WANG Changcheng1, WANG Yunjia2, CHEN Guoliang2
(1. School of Geosciences and Info-Physics, Central South University, Changsha410083, China; 2. Key Laboratory of Resources and Information Engineering of Jiangsu Province, China University of Mining and Technology, Xuzhou 221116, China)
To reduce the unreliability of the law of kinematic mining subsidence derived from leveling measurements with temporal feature points loss, the integrated new interferometric synthetic aperture radar (InSAR) and traditional leveling measurements with Logistic time function and Levenberg-Marquard (LM) algorithm were proposed, and the law of kinematic mining subsidence and the relationship between the law and underground extraction were analyzed. The results show that the mean square errors (MSE) of fitted subsidence and acceleration using InSAR and leveling measurement are 89.0% and 97.9% higher, respectively, than that only using leveling observations with temporal feature points loss. Logistic model can fit the kinematic subsidence of a ground point greatly well, and there is linear relationship between the occuring time of the maximum velocity and acceleration extremum of fitted Logistic time function and that of advancing working panel under the observation point, respectively.
InSAR; leveling; kinematic mining subsidence; Logistic time function
10.11817/j.issn.1672-7207.2015.10.026
TP237
A
1672−7207(2015)10−3743−09
2014−10−10;
2014−12−22
国家自然科学基金资助项目(41222027,40974006);国家高技术研究发展计划(863计划)项目(2012AA121301);湖南省杰出青年科学基金资助项目(13JJ1006);国土资源部公益基金资助项目(201211011);中央高校基本科研业务费专项资金资助项目(2013zzts249)(Projects (41222027, 40974006)supported by the National Natural Science Foundation of China; Project(2012AA121301)supported by the National High Technology Research and Development Program(863 Program) of China; Project(13JJ1006)supported by Outstanding Young Science Foundation of Hunan Province; Project(201211011) supported by the Public Welfare Fund of Ministry of Land and Resources;Project(2013zzts249) supported bythe Fundamental Research Funds of Central Universities)
朱建军,教授,从事InSAR、测量平差及数据处理研究;E-mail:zjj@mail.csu.edu.cn
(编辑 陈灿华)
