双基高比线面阵结合立体测绘几何模型的构建

李瀛搏 胡斌 胡海彦 方勇 傅丹膺

（1 北京空间机电研究所，北京 100094）

（2 西安测绘研究所，西安 710054）

（3 航天东方红卫星有限公司，北京 100094）

0 引言

航天立体测绘卫星系统作为航天对地观测系统的重要组成部分，用于获取全球范围目标的精确地理信息数据，为国家基础地理信息系统的建设、维护和更新提供数据源，满足国家基础测绘、国土资源调查以及国民经济建设等各个方面的需求[1-2]。

大比例尺航天立体测绘主要用于全球范围重点目标区域地表三维信息获取，主要任务是实现城市等重点目标及其设施和相关区域地物目标的三维结构重建，目标特点是建筑物密集、高度起伏变化剧烈[3]，采用传统的大基高比摄影测量模式存在以下3个方面的难题：

1）由于地表高程的剧烈变化造成地物之间相互遮挡，需要多视角观测，在有限的观测条件下，容易造成有效信息的缺失。

2）由于大基高比测绘采用大交会角观测，造成立体像对之间几何和辐射差异非常大，影响了同名像点的匹配精度，同时三维信息重建自动化程度较低。

3）比例尺越大，对地物要素信息的表达越详细、影像分辨率越高、几何精度越高，因此，对光学测绘卫星系统的综合性能提出了更高的要求，体积和质量明显增加，系统设计和研制的难度也会显著增大[4]。

因此，本文提出了基于双基高比线面阵结合的立体测绘方法。采用大、小基高比的双基高比立体测绘相机可以实现大基高比交会成像和小基高比近同时成像的综合成像模式，兼顾了平缓地形测绘和地表陡峭地物三维测绘要求，可以降低建筑物遮挡带来的问题，有利于提高影像匹配精度和自动化处理程度，在城市大比例尺立体测绘中有更多优势。同时，由于面阵探测器具有较好的几何保真度，线阵加入面阵形成线面阵联合相机系统后，立体定位的可靠度和精度将得到明显提高，兼顾了正射影像等测绘产品的制作，有利于实现无地面控制点高精度全球测绘[5]。

本文以共线条件方程为基础，从理论上分析面阵相机和线阵相机的成像机制，建立双基高比线面阵结合立体测绘的传感器严格几何成像模型，并基于仿真影像进行双基高比线面阵结合定位精度分析，验证成像模型的正确性，可为我国实现1︰5 000比例尺甚高精度航天立体测绘提供一种新思路和解决途径。

1 线面阵联合成像模型的构建

严格成像模型是以共线方程为基础，通过不同坐标系之间转换，严格描述像点的空间坐标与相应地面点的数学关系。因此，根据传感器成像几何特性的不同，所对应的严格成像模型也有所不同。

1.1 面阵相机严格成像模型

面阵影像的成像过程为面中心投影，每景影像仅有一个投影中心[6]。影像覆盖范围内的地面点通过投影中心（像主点S）进入传感器内部，在像平面上形成影像。

基于中心投影原理，像点和物点的向量关系如图1所示，共线方程为

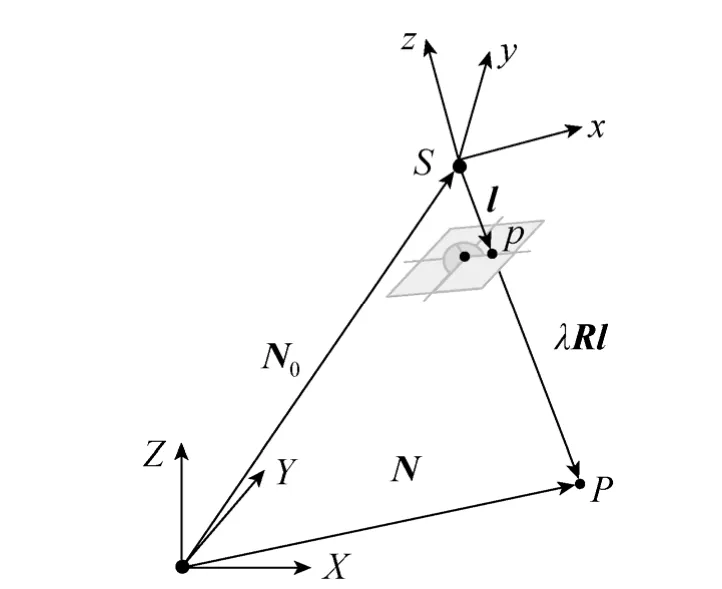
图1 共线方程向量式Fig.1 Vector diagram of collinearity equation

地面点 P (X,Y,Z)和像点 p (x,y,z)以及投影中心S三点共线，根据共线条件方程，则面阵影像的严格模型为

考虑到系统误差，上式扩展为

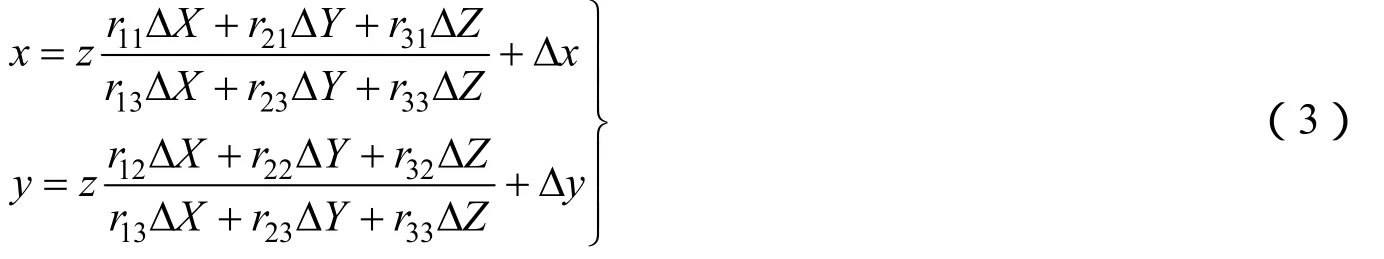
为考虑到系统误差的数学模型，系统误差数学模型和这些附加参数是根据相机系统误差的实际物理几何特性来确定的，对于复杂的系统误差也可采用高阶多项式来描述，附加参数的有效性需要实际的试验和数据平差处理来确定。共线方程的一般式可表示为

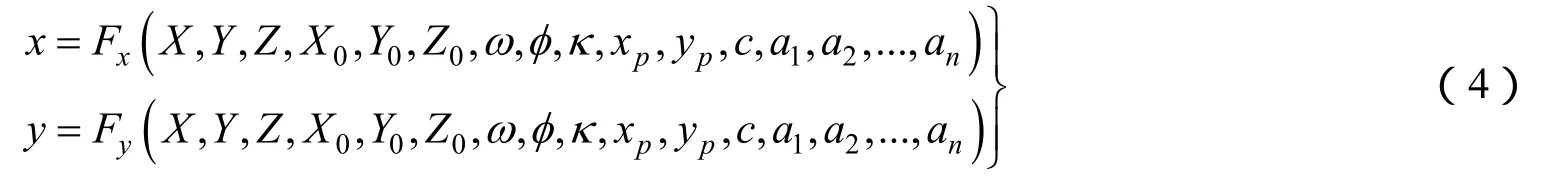
式中 ω、φ、κ为像空间坐标系（相机坐标系）和物方空间坐标系的旋转变换角；xp、yp、c为相机内方位元素；xF、yF为考虑系统误差的共线方程一般表达式。

1.2 线阵相机严格成像模型

与面阵相机的成像方式不同，线阵影像是由一系列垂直于轨道方向的线阵 CCD传感器通过推扫的方式获取的，通过卫星沿轨飞行，获得所摄地区的连续航带影像。因此，一幅影像上像点坐标对应的外方位元素并不唯一，每一扫描行图像与被摄物体之间存在着中心投影关系，都对应独立的一套外方位元素

1.2.1 线中心投影共线方程模型

对于单个像点，线阵相机和地面点的数学关系为

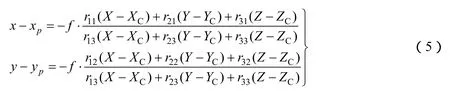
式中 (XC，YC，ZC)为投影中心在地面坐标系统中的坐标；f为相机焦距。

对于光学系统由多个镜头组成的传感器，对上述模型需要改化，引入附加参数以描述其他镜头相对于正视镜头的位置与姿态关系。例如，对于镜头j（j=1, 2, 3, …, n），以dxj、dyj、dzj为相对于正视镜头的相对位置，αj、βj、γj为相对于正视镜头的相对姿态，如图2所示，图中fj、xpj、ypj为镜头j的焦距和主点坐标[7-10]，PCj、xCj、yCj、zCj为相机j的像空间坐标，则公式扩展为

即

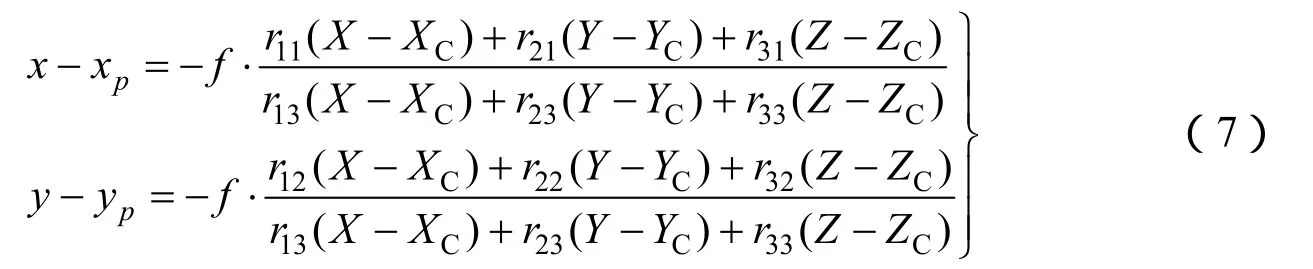
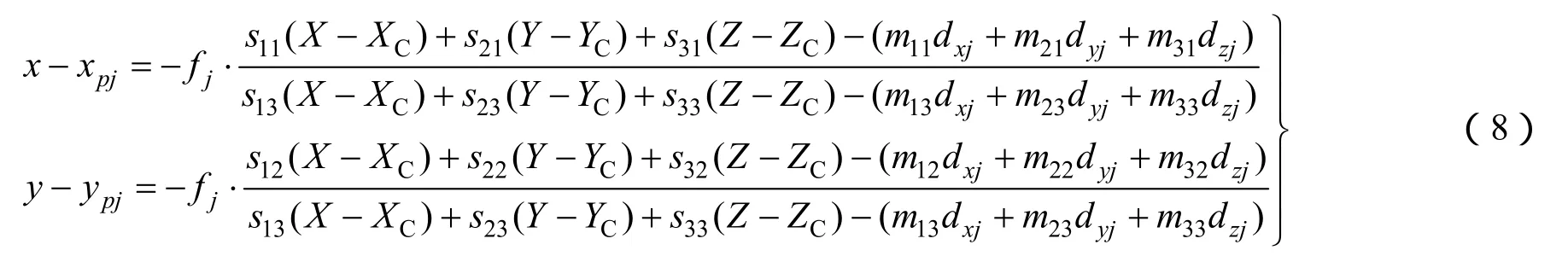
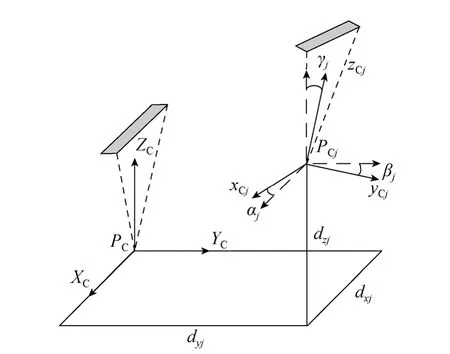
图2 相机j与正视镜头的几何位置相对关系Fig.2 Positional relationship between camera j and nadir camera

考虑到相机自检校，上述模型可进一步扩展为

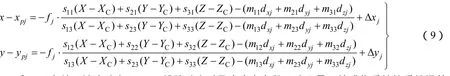
式中 Δxj和Δyj为关于镜头畸变、CCD线阵畸变以及内定向参数（改正量）等成像系统的系统误差模型。

1.2.2 线阵相机轨道模型

传感器外部定向模型（EO）用关于时间的分段多项式（PPM）来建模[11]。可以通过卫星飞行轨道的特性设置多项式阶数，根据控制点（GCPs）和连接点（TPs）的分布来确定多项式的分段个数，分段多项式轨道模型如图3所示。

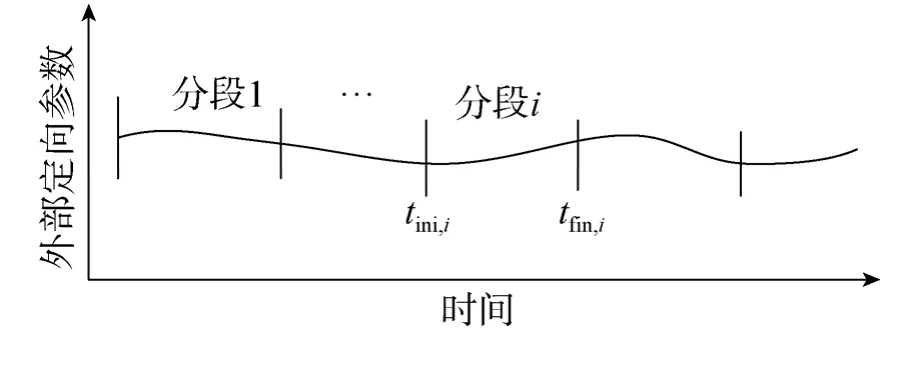
图3 分段多项式轨道模型Fig.3 Orbit model of sectioned polynomial

对于被分割轨道的第i段（该段的首末端点的线阵影像获取时刻记为），则定义时间变量t为

式中0t为该段轨道上某线阵影像的获取时刻。以2阶多项式为例（时间t为因变量），则在分段多项式的每一段，传感器外部定向参数模型为

1.3 附加参数模型

为了提高模型对传感器的物理描述真实度，需要对基本的共线方程进行扩展，以期达到精细化建模的目的。具体做法是对共线方程引入附加参数，这些附加参数在平差处理过程同时予以求解。附加参数必须满足3个要求：1）所有新引入的参数必须与已存在的平差中的待估参数无关；2）如果引入的附加参数模型为多项式，多项式阶数不宜过高；3）还需要使用统计方法对引入的参数进行显著性检验，以确定各个附加参数对整个模型贡献的显著性。

根据附加参数是否具有实际的物理意义，可以将像差改进模型分为顾及像点特性的系统误差改正模型和多项式误差改正模型两大类。测绘相机系统误差的一般表达式为

像差改进模型是关于像空间坐标的函数，利用相机自身物理参数或正交化参数来予以描述，最终反映理想的像空间坐标和实际的像点坐标之间的差异。

顾及像点特性的这类系统误差模型是从实际的物理、几何特性出发来描述和刻画尽可能与实际相机相符的系统误差数学模型。

通过分析测绘卫星系统的误差源，可以将上式展开为

式中 Δxi、Δyi为内定向参数误差（主点、主距）；Δxr、Δyr为镜头的径向畸变；Δxd、Δyd为镜头的偏心畸变；Δxf、Δyf为成像面内误差（像元尺寸均匀度、阵列正交性）；Δxu、Δyu为成像面误差（像面平整度）。

由于线阵相机与面阵相机在系统组成上的区别，其附加参数也不相同。线阵相机通常采用多个线阵传感器拼接来获得足够的成像幅宽，因此，需要对多个线阵传感器之间的直线度误差和拼接精度进行分析和建模。

1.4 线面阵联合成像模型

混合型的线面阵相机组合，从数学模型上来讲，是将线阵、面阵不同传感器模型及其成像模式结合在一起，在数据平差处理时，其观测方程组的建立，系数矩阵的构造等与前两者存在一定的差异，这是线面阵相机的数据平差处理的“组合”，其本质是“多源数据联合平差空中三角测量”问题[12-13]。

对于如图4所示的线面阵结合相机系统，如果地面点A分别成像在线阵影像及面阵影像上，则面阵相机成像模型、线阵相机成像模型组成联立方程组。

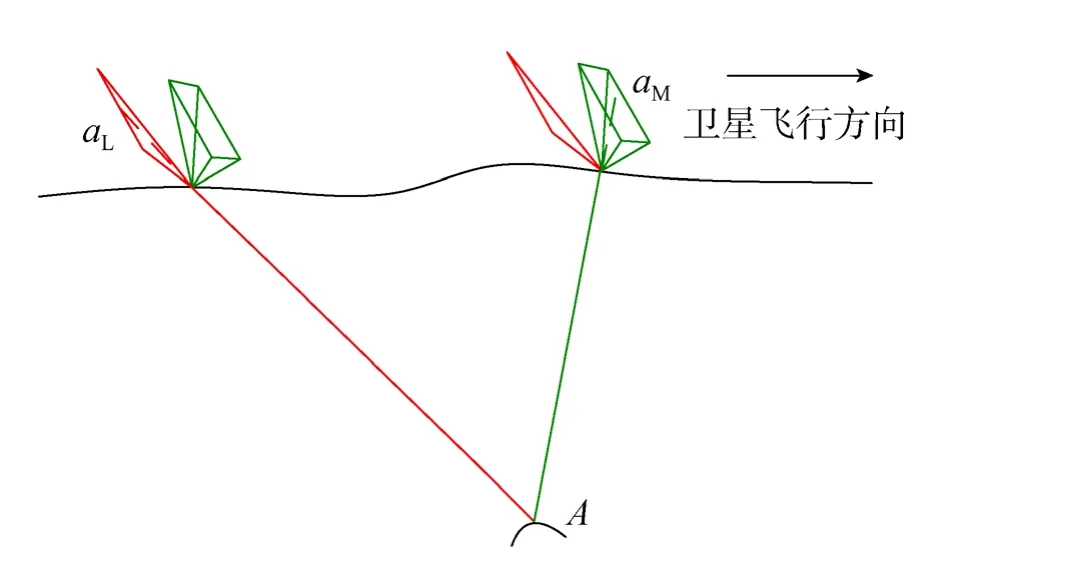
图4 双基高比线面阵结合相机系统立体定位示意（以一个线阵和一个面阵为例）Fig.4 Double baseline stereo photogrammetric mode（one linear array sensor and one area array sensor）

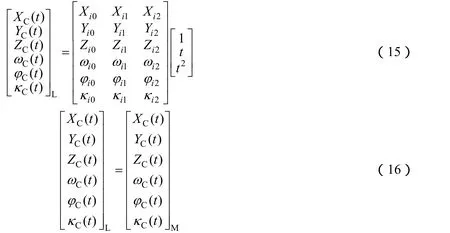
式中 下标M、L分别为面阵相机和线阵相机。式（16）为线（面）阵相机摄影时刻约束方程，由于线阵相机与面阵相机安装在同一卫星平台上，因此，在同一摄影时刻 t，线阵相机与面阵相机具有相同的外方位元素。

式（14）联立的条件是线面阵相机对同一物点A在不同摄影时刻进行摄影成像，需要注意线阵相机影像tax坐标与时间t等价。如果面阵相机能够形成连续立体模型（连续航向重叠）或单张影像覆盖3个以上控制点，则可由面阵相机的摄影航带进行区域网平差或单片后交，从而计算得到面阵相机在某些摄影时刻的外方位元素，而且这些摄影时刻需要正确记录，进而利用式（16）进行线（面）阵相机摄影时刻约束。由于式（14）为非线性系统，需要采用牛顿迭代法平差求解，线性化后对于摄影区域的多个控制点及对应的多个面阵影像及线阵条带影像，会有如下线性化后的观测方程组：

式中 H为未知数向量；E为系数矩阵；L为观测量；v为观测量改正数。

其中

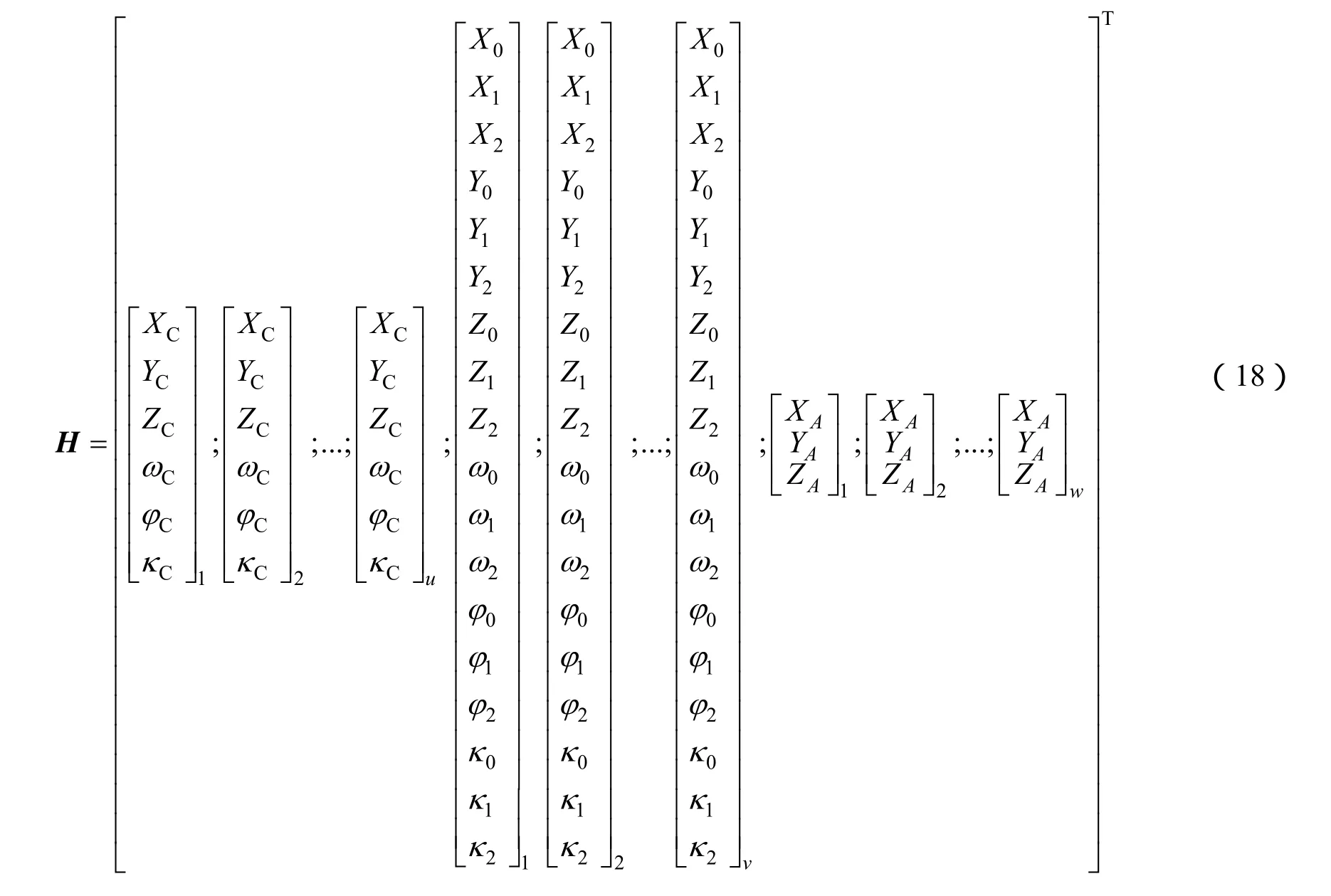
式（18）中，未知数H可以分为3类：1）面阵相机外方位元素（u为面阵相机镜头数）；2）线阵相机轨道模型参数（v为线阵相机镜头数）；3）物点物方坐标（w为物点数）。至此，平差精度（内部精度）的评估可按最小二乘技术中的相关内容进行；外部精度（检查精度）按RMS计算而得。

通过理论建模，本文提出了双基高比线面阵结合立体测绘严格几何模型，既可以解决线阵、面阵不同类型传感器结合的测绘数据处理和高精度定位问题，也可以解决大、小基高比不同探测模式的数据处理和平差解算。

2 基于仿真影像的双基高比线面阵结合定位精度分析

2.1 仿真场景建立

本文利用 SE-Workbench软件实现遥感器成像仿真过程中三维场景的构建，利用软件仿真模拟大、小基高比条件下光学遥感器的立体成像过程[14-15]，采用高精度亚像素视差相关匹配处理方法处理过程，从仿真分析的角度验证小基高比和双基高比立体测绘的可行性，对双基高比线面阵结合的立体测绘成像模式进行研究。

试验采用的仿真场景如图5所示，场景包含三维控制点21个，具有不同高度的城市建筑12组。影像分辨率为 0.3m。基于该场景，对五种成像模式进行对比分析，分别为小基高比 0.05两面阵相机成像模式、大基高比双线阵两相机联合成像模式（基高比0.6）、大小基高比两线阵一面阵三相机联合成像模式、大小基高比四相机联合联合成像模式和线面阵两相机联合成像模式进行了定位精度分析。从仿真途径验证双基高比线面阵结合立体测绘严格几何模型的正确性，分析不同测绘模式相对于传统测绘方法的优势。

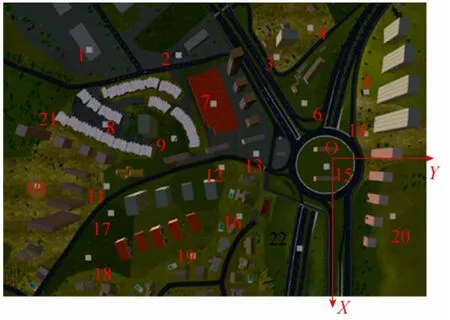
图5 控制场的控制点与检查点点位分布情况Fig.5 The distribution of controls points and check points in control field

2.2 小基高比0.05面阵试验结果

小基高比 0.05两面阵相机成像模式的立体定位精度结果如表 1所示，对应的像点量测精度为 1/20像元。

表1 基高比0.05面阵相机立体定位检查点精度统计（像点量测精度1/20像元）Tab.1 Stereo positioning accuracy of baseline 0.05 area array camera (matching in sub-pixel precisions)

为了进行不同像点量测精度对定位精度的影响研究，以高精度像点匹配为基础（像点量测精度约1/20像元），加入高斯白噪声，形成了量测精度在1/20～1/2像元范围的6组不同的像点数据，并进行定位实验检查点的三维定位精度见表2。

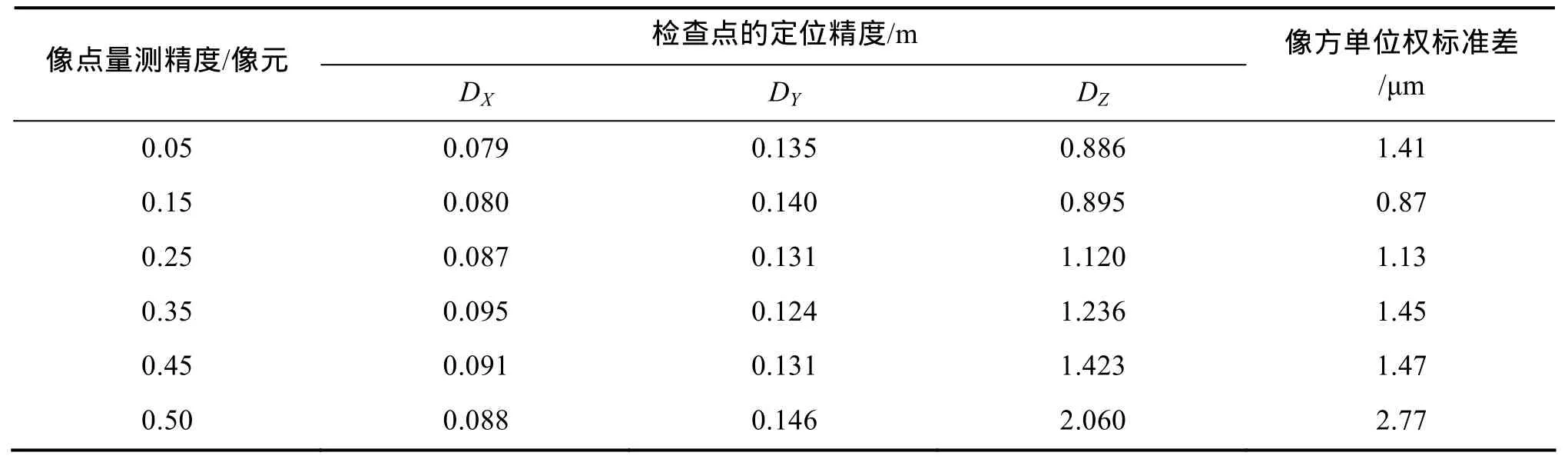
表2 不同像点匹配精度下基高比0.05面阵相机立体定位检查点精度统计Tab. 2 Stereo positioning accuracy of baseline 0.05 area array camera（different matching precisions）

从图6可以看出，采用本文提出的严格几何模型进行小基高比解算，在匹配精度为1/20像元条件下，高程精度为0.886m。在基高比为0.05的条件下，随着像对匹配精度的提高（1/20～1/2像元），导致视差精度的提高，高程精度明显提高，但匹配精度的提高和高程精度的提高不是正比关系，匹配精度提高10倍，高程精度提高约1倍。该仿真试验证明了严格几何模型可以满足小基高比条件下的数据处理和目标三维定位。

图6 不同像点量测（匹配）精度下基高比0.05面阵相机立体定位检查点精度统计Fig.6 Stereo positioning accuracy of baseline 0.05 area array camera in different matching precisions

2.3 大小基高比线面阵结合相机方案优选

本文分析了4种不同的大小基高比线面阵结合成像方案，具体相机形式如图7所示。

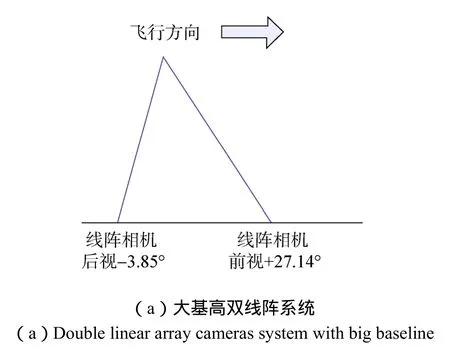
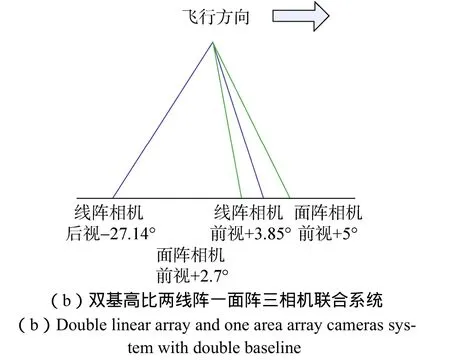
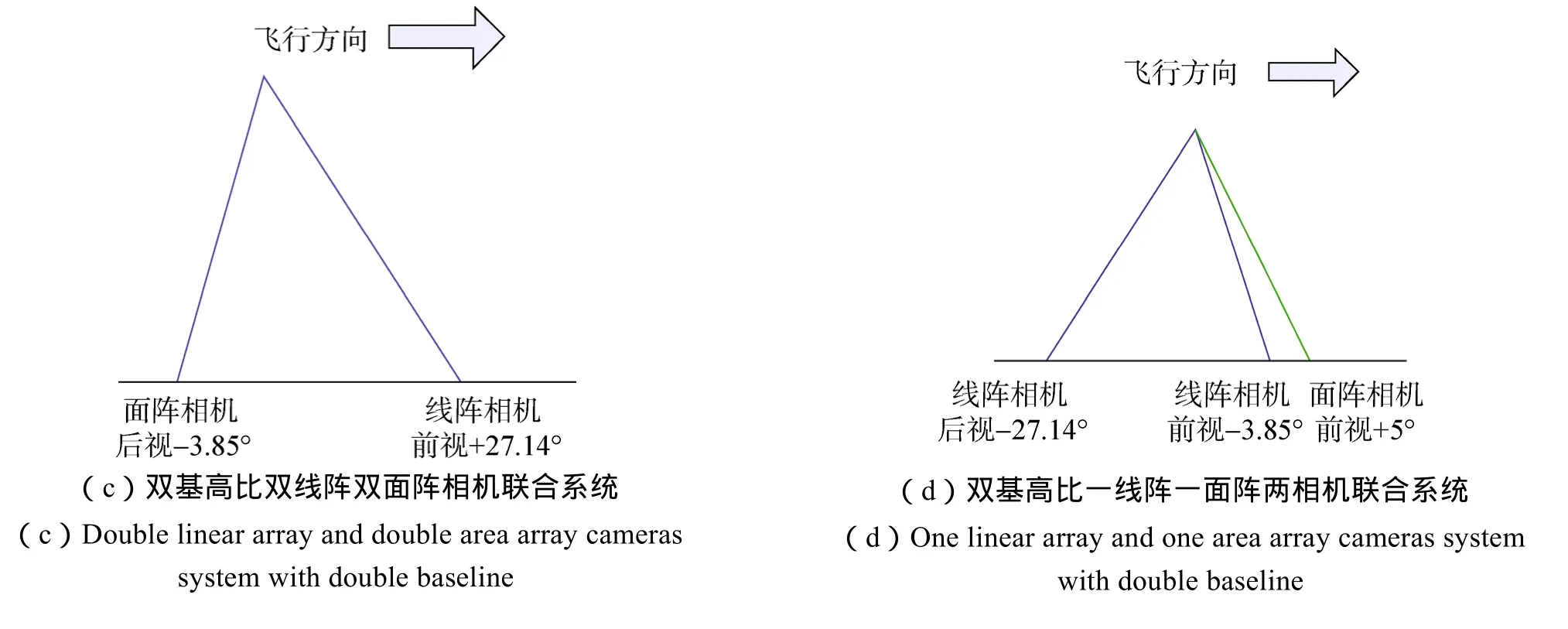
图7 4种大小基高比线面阵成像方案Fig.7 Diagram of four imaging plans of double baseline photogrammetry

仿真结果得到4种大小基高比线面阵成像方案定位精度结果，如图8所示。可以看出，单/双线阵相机引入同等幅宽单/双面阵，定位精度明显提升，且定位精度相当；而单线阵引入等幅宽单面阵相机（基高比0.6），相机系统形式相对而言最为简单，因此，一线阵一面阵两相机联合具有较明显的优势。

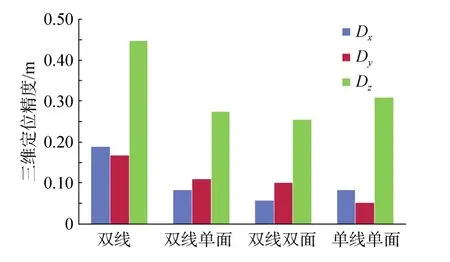
图8 4种线面阵方案定位精度比较Fig.8 Comparison of four imaging plans of double baseline photogrammetry

3 结束语

本文以共线方程的严密成像理论为基础，将面阵中心投影共线方程和适用于线阵列影像的扩展共线方程进行整合，提出了双基高比线面阵结合测绘方法，分析了系统误差补偿方法，建立了考虑系统误差的联合严格几何成像模型，完成了基于仿真影像的双基高比线面阵结合定位精度分析，初步研究表明：

1）引入等幅宽面阵联合平差，可提高线阵影像的内部精度。

2）相比双线阵相机，立体定位的精度和解算的可靠度明显提高。采用亚像素高精度量测算法可进一步提高定位精度。

3）双基高比线面阵相机可有效避免遮挡和死区对立体测绘的影响，对城市地区高大建筑物具有更好的量测性能，在提升定位精度的同时，兼顾了面阵正射影像等测绘产品的制作。

4）单线阵相机引入同等幅宽单面阵（0.6基高比）的测绘模式，可以作为未来甚高精度测绘的有效解决途径之一。

5）通过仿真分析验证了双基高比线面阵结合立体测绘的传感器严格几何成像模型的正确性，该模型既可以解决线阵、面阵不同类型传感器结合的测绘数据处理和高精度定位问题，也可以解决大、小基高比不同探测模式的数据处理和平差解算，为甚高精度航天测绘应用提供理论依据。

References)

[1]唐新明, 谢俊峰, 张过. 测绘卫星技术总体发展和现状[J]. 航天返回与遥感, 2012, 33(3): 17-24.TANG Xinming, XIE Junfeng, ZHANG Guo. Development and Status of Mapping Satellite Technology[J]. Spacecraft Recovery amp; Remote Sensing, 2012, 33(3): 17-24. (in Chinese)

[2]王任享. 中国无地面控制点摄影测量卫星追述(二)——1:1万传输型摄影测量卫星技术思考[J]. 航天返回与遥感,2014, 35(2): 1-5.WANG Renxiang. Chinese Photogrammetry Satellite without Ground Control Points(2)——Technical Thinking of 1:10 000 Scale Data-transferring Photogrammetry Satellite[J]. Spacecraft Recovery amp; Remote Sensing, 2014, 35(2): 1-5.(in Chinese)

[3]方勇, 李瀛搏. 高分辨率大面阵相机航天测绘应用立体探测模式分析[J]. 测绘科学技术学报, 2011, 28(4): 235-240.FANG Yong, LI Yingbo. Application Modes Analysis of High Resolution Large Plane Array Digital Camera in Space Photogrammetry[J]. Journal of Geomatics Science and Technology, 2011, 28(4): 235-240. (in Chinese)

[4]张月, 胡斌, 阮宁娟. 双基高比立体测绘相机热分析与热设计[J]. 红外与激光工程, 2013, 42(12): 3270-3276.ZHANG Yue, HU Bin, RUAN Ningjuan. Thermal Design of Stereopsis Camera with Double Baseline[J]. Infrared and Laser Engineering, 2013, 42(12): 3270-3276. (in Chinese)

[5]李瀛搏, 傅丹膺, 李博. 甚高精度空间立体测绘体制技术途径研究[C]. 第19届中国遥感大会. 西安: 中国宇航学会,2014.LI Yingbo, FU Danying, LI Bo. Research on the Technical Approach for Space Stereo-mapping System with Very High Accuracy[C]. 19th Conference on Remote Sensing of China. Xi’an: Chinese Society of Astronautics, 2014. (in Chinese)

[6]王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社, 2007.WANG Zhizhuo. Principles of Photogrammetry[M]. Wuhan: Wuhan University Press, 2007. (in Chinese)

[7]李德仁, 王密. “资源三号”卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33(3): 1-6.LI Deren, WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J]. Spacecraft Recovery amp;Remote Sensing, 2012, 33(3): 1-6. (in Chinese)

[8]闫利, 姜芸, 王军. 利用视线向量的资源三号卫星影像严格几何处理模型[J]. 武汉大学学报, 2013, 38(12): 1451-1455.YAN Li, JIANG Yun, WANG Jun. Building of Rigorous Geometric Processing Model Based on Line-of-sight Vector of ZY-3 Imagery[J]. Geometrics and Information Science of Wuhan University, 2013, 38(12): 1451-1455. (in Chinese)

[9]王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2006.WANG Renxiang. Satellite Photogrammetry Principle for Three-line-array CCD Images[M]. Beijing: Surveying and Mapping Press, 2006. (in Chinese)

[10]余俊鹏, 高卫军, 孙世君, 等. 三线阵相机体系定向模型研究[J]. 航天返回与遥感, 2013, 34(1): 44-51.YU Junpeng, GAO Weijun, SUN Shijun, etal. Research of Orientation Model of Three-linear-array Camera System[J].Spacecraft Recovery amp; Remote Sensing, 2013, 34(1): 44-51. (in Chinese)

[11]Light D L. Characteristics of Remote Sensors for Mapping and Earth Science Applications[J]. Photogrammetric Engineering amp; Remote Sensing, 1990, 56(12): 1613-1623.

[12]李然. 多源遥感影像的联合平差[D]. 武汉: 武汉大学, 2012.LI Ran. Combined Adjustment of Multi-source Remote Sensing Imagery[D]. Wuhan: Wuhan University, 2012. (in Chinese)

[13]Raggam J, Almer A. Mathematical Aspects of Multi-sensor Stereo Mapping[C]. IGARSS’ 90, Washington D. C.

[14]Julie D, Bernard R. Small Baseline Stereovision[J]. Journal of Mathematical Imaging and Vision, 2007, 28(3): 209-223.

[15]范大昭, 申二华, 李禄, 等. 基于相位相关的小基高比影像匹配方法[J]. 测绘科学技术学报, 2013, 30(2): 154-157.FAN Dazhao, SHEN Erhua, LI Lu, etal. Small Baseline Stereo Matching Method Based on Phase Correlation[J]. Journal of Geomatics Science and Technology, 2013, 30(2): 154-157. (in Chinese)