基于空域的自适应MTFC遥感图像复原算法

周楠 齐文雯 曹世翔 何红艳 邢坤 岳春宇

（北京空间机电研究所，北京 100094）

0 引言

“高分二号”（GF-2）卫星是我国自主研发的首颗空间分辨率优于1m的民用光学遥感卫星。为了满足轻小型高分辨率相机的研制要求，采用小相对孔径（大F数）相机系统设计；同时，遥感图像成像过程中，受到大气环境、光学系统、探测器、平台运动和电路等因素的影响[1-3]，导致调制传递函数（modulation transfer function，MTF）的下降，引起图像品质退化。因此，为了使相机图像更加完美地展现出亚米级的优势，GF-2卫星从天地一体化设计角度出发，确定采用地面调制传递函数补偿法（modulation transfer function compensation，MTFC）的方式对退化后的图像进行复原。

图像复原就是去除或者减轻图像获取过程中发生的像质退化，使图像趋向于没有退化的理想图像。由于图像退化的原因可能有很多种，如光电传感器的非线性、物体与摄像机间的相对运动、大气的扰动等，因此根据不同的退化原因，出现了很多种图像复原方法，如逆滤波[4-6]（去卷积）、维纳滤波[7]、约束最小平方滤波[8]等。

国外的MTFC技术较成熟，美国研制的亚米级商业遥感卫星，包括IKONOS、QuickBird-2、OrbView-3和GeoEye-1等都成功地应用了地面MTFC技术，图像品质得到显著提升。国内也开展了MTFC技术的相关研究，文献[9]基于MTF理论的遥感图像复原研究，提出了一种基于MTF理论的图像复原方法，该方法主要包括去噪和 MTF拉伸两部分，针对遥感图像的特点，提出了一种基于频域的去噪方法；为了能够调节频谱拉伸的程度，还给出了一种指数调节曲线的方法。文献[10]针对遥感图像在成像与传输过程中的退化而导致的图像模糊与噪声干扰，提出了一种基于 MTF估算与总变分优化的图像恢复方法。文献[11]针对 TDI-CCD成像数据的特点，从遥感图像中获取刃边来计算成像系统的 MTF，采用维纳滤波法对退化图像进行MTF补偿处理。

MTFC在提升系统MTF的同时，必然导致图像信噪比（signal to noise ratio，SNR）下降。目前MTFC研究主要集中于MTF曲线获取和构造MTF补偿曲线，但是对于如何精确计算MTFC卷积核和噪声抑制研究甚少。鉴于此，本文提出一种MTFC复原算法，即根据实验室实测的MTF值以及用户的需求确定相机不同频率处 MTF的补偿值，依据有限长脉冲响应原理，计算获取一维卷积系数；在此基础上，精确构造二维卷积核对图像进行卷积处理。卷积处理时以实验室实测的相机不同成像参数下不同灰度的SNR信息和不同的景物内容为约束进行自适应抑噪，在提升图像MTF的同时保证图像的SNR。

1 图像品质退化

假定 (,)fxy为原目标图像[12-13]， (,)gxy为观察到的退化图像，则

式中 (,)hxy为点扩散函数；符号*表示卷积。

式（1）表示原图像通过与相应的点扩散函数作卷积而得到退化图像的的过程。对式（1）两边同时作傅里叶变换则得到

式中 (,)Guv为 (,)gxy的傅里叶变换； (,)Fuv为 (,)fxy的傅里叶变换； (,)Huv为 (,)hxy的傅里叶变换，它的值为复数，可以表示成

式中 |(,)Huv|是幅值；φ为相位。若对幅值做归一化，使得零频率的幅值为 1，则归一化的幅值为MTF，即

式中 k为 (,)Huv在零频率的幅值。由式（2）～（4）得

假定MTF在作用于 (,)Fuv时，其与频谱中心为圆心的等半径圆上的MTF值相同，则可以将式（5）简化为

上面的图像品质退化过程是假定没有噪声的理想情况。实际成像过程中，噪声的引入是不可避免的，假定噪声图像为 (,)bxy，则式（1）应改写为

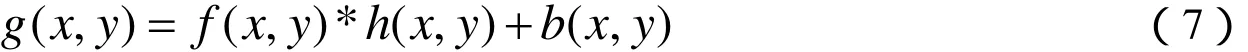
相应地由式（7）可得

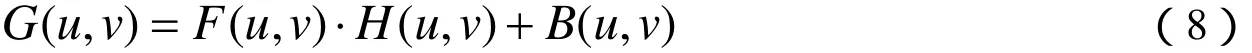
式中 (,)Buv为 (,)bxy的傅里叶变换。

式（6）可改写为

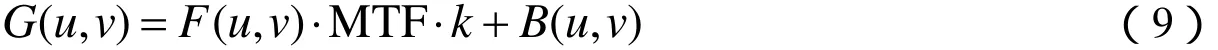
式（9）为最终的图像品质退化公式。

2 自适空域MTFC图像复原算法

自适应空域MTFC复原算法流程如图1所示。

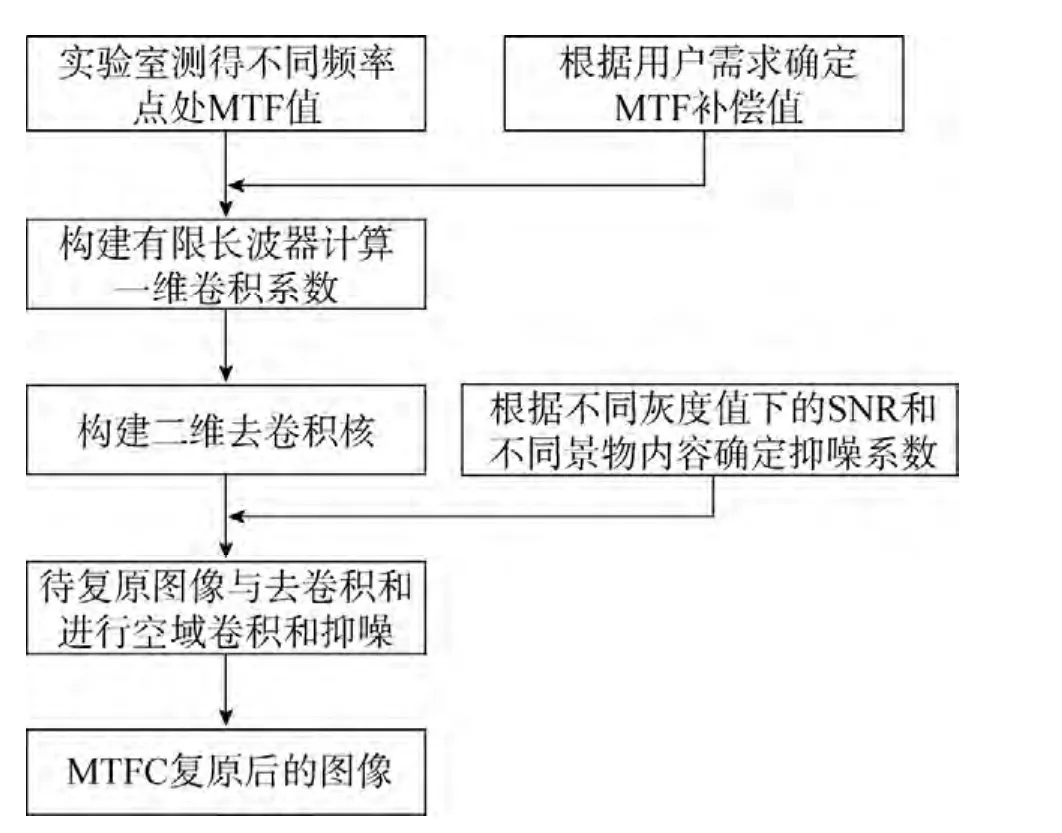
图1 自适应空域MTFC图像复原算法流程Fig.1 Adaptive MTFC image restoration algorithm flow

复原算法步骤：

1）根据实验室实测得到的相机不同频率处的MTF值以及用户需求确定的MTF补偿值，构建一维有限长脉冲响应，计算一维卷积系数；

2）利用步骤1）得到的一维卷积系数，构造二维卷积核；

3）利用实验室实测的相机不同成像参数下确定的不同灰度的SNR信息，计算抑噪查找表系数；

4）利用步骤3）得到的抑噪查找表系数，计算抑噪阈值；

5）对待复原的图像进行卷积处理，卷积处理时利用步骤4）得到的抑噪阈值以及景物内容进行自适应抑噪处理。

2.1 卷积系数

卷积系数的构建对于MTFC复原算法至关重要，如何精确快速的计算卷积系数是本文研究的重点之一。本文采用实验室实测的相机不同频率的 MTF值，构建有限长脉冲响应，计算滤波系数，较传统的利用傅里叶方法更加简洁精确、快速，可以针对不同频率进行精确补偿。

2.1.1 一维卷积系数

一维卷积系数的计算根据相机不同频率处实验室测得的静态 MTF值以及用户需求确定的不同频率处MTF的补偿值构造一维有限长脉冲响应[14-15]。

式中 ()Xn为一维卷积系数，是中心对称的，其长度本文取11（注：滤波系数的长度影响处理效果。根据计算资源和处理时间要求，实际情况应综合考虑选择滤波系数长度）；取N为正整数；为不同频率处的MTF补偿值。

2.1.2 二维卷积核

利用步骤2.1.1节得到的一维卷积系数 ()Xn构造二维卷积核 (,)Xij， (,)Xij为一个N×N的正方形矩阵且满足中心对称和轴对称，其中i，j的取值范围分别为中不同的卷积系数的个数为，1/2象限的二维频域响应函数可表示为：

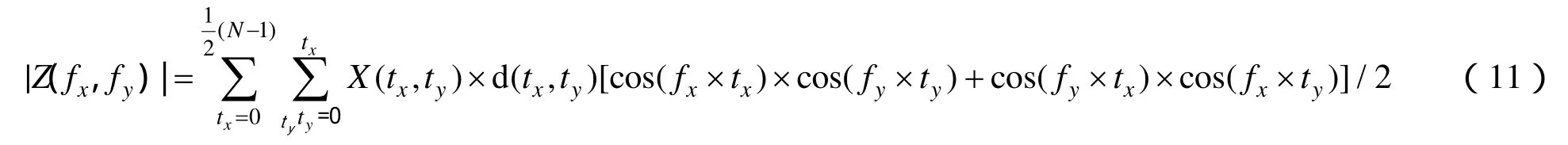
2.2 抑噪处理

图像进行MTFC复原时，在提升图像清晰度的同时必然导致信噪比下降。因此，如何把噪声抑制在较低的水平也是本文算法研究的重点之一。算法在进行抑噪处理时引入实验室实测的相机不同成像参数下确定的不同灰度值的SNR信息作为抑噪的约束。该方法克服了传统抑噪方法的盲目性，在提升图像清晰度的同时有效保证图像SNR。

式（12）所示为算法采用的抑噪基本原理:

式中 s0为原始图像灰度值；s1为直接利用二维卷积核卷积处理后结果值；s2为进行抑噪处理后的结果值；K为抑噪阈值。当K gt;1时，判断结果高于抑噪阈值的像元（即该像元附近高频信息较丰富），此时作全额补偿(此种情况下相当于不做抑噪处理)，若 K lt;1，说明判断结果低于抑噪阈值的像元（即该像元附近高频信息较少），只进行适当补偿，即做一定程度的抑噪处理。

2.2.1 抑噪查找表

抑噪查找表的建立主要依据实验室实测的相机不同成像参数下确定的不同灰度值的SNR信息，建立抑噪查找表系数矩阵M，如式（13）所示，M是关于灰度值s0的函数。

式中0()Ys 为灰度值对应的SNR，由实验室定标图像实测的至少6组不同灰度等级下的SNR值，拟合得到各个灰度值下的SNR曲线；Ymax为该组相机参数状态下最大的SNR。

2.2.2 抑噪阈值

一般来说，平坦区域，高频部分中噪声所占比例较大，灰度层次丰富的区域，高频部分中噪声所占比例相对较小。抑噪阈值的确定与抑噪查找表和图像灰度层次丰富程度相关。

3 试验结果与分析

3.1 MTFC试验结果

为了验证本文算法的正确性与有效性，试验采用 GF-2卫星全色谱段图像，图像经过相对辐射校正处理。对复原后的图像品质的评价方法采用主、客观评价相结合。主观评价主要通过目视解译的方式查看图像的色调、纹理、边缘等信息是否改善以及复原后图像是否有异常现象出现。客观评价采用图像均值、方差、信息熵、对比度和边缘能量5种客观指标进行对比分析。

图2所示为采用本文MTFC算法复原后的结果图像，从目视解译角度可以发现复原后图像并无异常现象出现，并且地物边界、轮廓以及图像细节更加突出，清晰度提升的同时无明显噪声出现。

图2 采用本文MTFC算法复原结果图像Fig.2 Restored result by using our proposed MTFC method

为了更客观地反映图像复原的效果，对复原前后图像的相关指标进行评价，如表1所示。

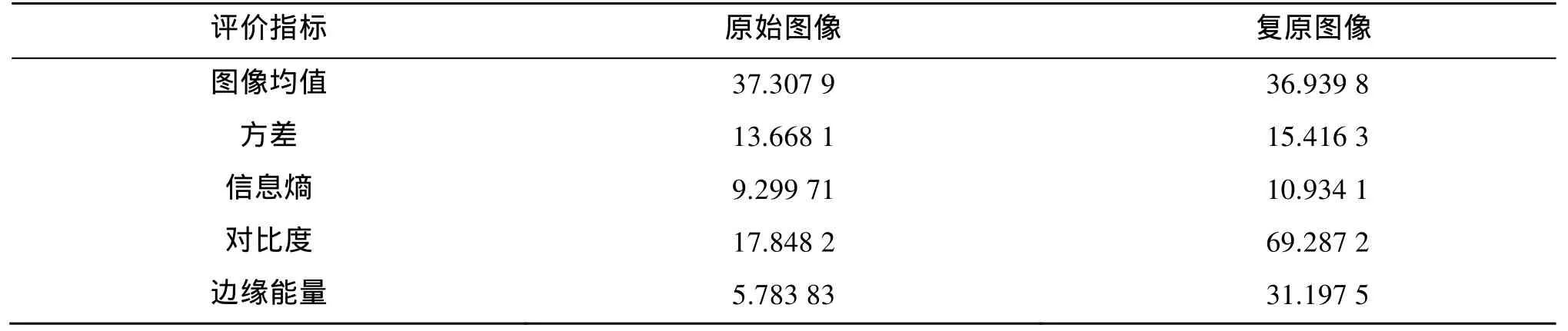
表1 复原前后图像比较结果Tab.1 Comparison of the images before and after restoration

从表1可以看出，复原后：图像均值变化很小，几乎可以忽略，表明复原结果整体灰度值并无明显变化；图像的方差增大，表明复原后图像的信息量有所增加；图像信息熵增大，表明复原后图像信息丰富程度提升，同样说明信息量增加。图像对比度显著增大，反映复原后图像中的微小细节与纹理信息丰富。图像边缘能量显著增大，表明复原后图像中边缘的丰富和清晰程度增大，纹理增多。

为了充分验证本文算法的适应性，针对不同地物类型的遥感图像利用本文算法进行验证试验，如图3～4所示。主客观评价结果与以上结果一致。

图3 采用本文MTFC算法复原结果图像Fig.3 Restored result by using the proposed MTFC method

图4 采用本文MTFC算法复原结果图像Fig.4 Restored result by using the proposed MTFC method

3.2 MTFC方法比较分析

为了验证本文算法的优越性，选取不同类型的图像同时采用3种方法进行MTFC处理。方法1取自文献[11]，采用一种基于MTF估算与总变分优化的图像复原方法；方法2取自文献[12]，采用刃边法计算图像 MTF，然后采用维纳滤波法对退化图像进 MTFC处理，同时采用自适应矩匹配方法以及自适应中值滤波算法来过滤噪声。图5为不同复原算法的处理结果图像。

图5 采用不同复原算法复原结果图像Fig.5 Restored results by using different recovering methods

为了客观地反映不同算法图像复原效果，对复原前后图像的相关指标进行评价，如表2所示。

从表2可以看出，本文算法与其他算法相比，提升MTF程度最大的情况下SNR下降却最小，充分说明本文算法在有效提升图像MTF的同时，能够有效抑制噪声，保证图像的SNR。本文算法复原后图像均值变化很小，方差增大，结果与 3.1节一致。表明复原结果整体灰度值并无明显变化，信息量有所增加。对比度显著增大，反映复原后图像中的微小细节与纹理信息增加。

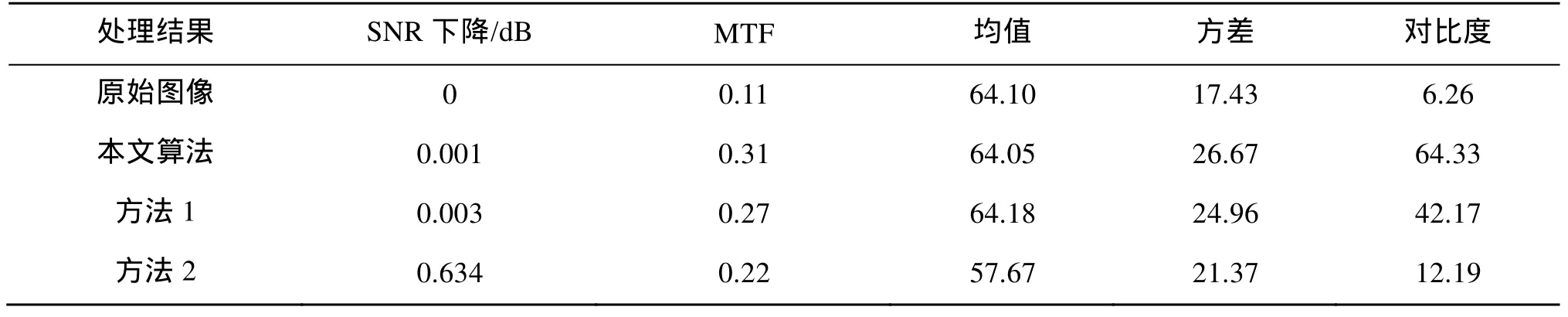
表2 不同算法复原结果比较Tab.2 Comparison of the image restored results of different methods

4 结束语

本文提出一种基于空域的自适应MTFC遥感图像复原算法，首先根据实验室实测的MTF值以及用户的需求值确定不同频率处 MTF的补偿值，构建有限长脉冲响应，计算卷积系数，较传统方法计算更加精确、简洁。同时，根据实验室实测的相机不同成像参数下确定的不同灰度的SNR和景物内容进行自适应抑噪，在提升图像清晰度的同时保证图像的SNR。通过试验验证本文算法的正确性和有效性。

本文算法也存在如下一些问题：

1）算法在进行图像复原时，在推扫方向和线阵方向补偿程度一致，这与实际情况不相符。因此，后续需改进二维卷积核，使得不同方向补偿程度不一样。

2）算法并未考虑大气湍流、平台振动引起的MTF下降问题，如何准确计算平台振动和大气湍流引起的MTF下降，从而进行准确补偿是后续研究的重点。

3）文中利用图像均值、方差、信息熵、对比度及边缘能量来评价影像的复原品质，但他们与实际复原效果并不能准确对应，并不是图像对比度越大，图像复原效果就越好。如何找到一个指标准确的评价图像复原品质，是今后研究的重点。

References)

[1]陈世平. 景物和成像条件对遥感图像品质的影响[J]. 航天返回与遥感, 2010, 31(1): 1-10.CHEN Shiping. The Effects on Remote Sensing Image Quality from Scenes and Imaging Conditions[J]. Spacecraft Recovery amp; Remote Sensing, 2010, 31(1): 1-10.(in Chinese)

[2]王彪, 姜志国, 赵丹培. 遥感图像运动模糊恢复方法及评价标准研究[J]. 航天返回与遥感, 2009, 30(3): 18-25.WANG Biao, JIANG Zhiguo, ZHAO Danpei. Research on Technologies and Quality Evaluation for Restoring Remote Sensing Motion-blurred Image[J]. Spacecraft Recovery amp; Remote Sensing, 2009, 30(3): 18-25. (in Chinese)

[3]陈奋, 赵忠明. 遥感影像反卷积复原处理[J]. 数字采集与处理, 2008, 23(2): 168-175.CHEN Fen, ZHAO Zhongming. Deconvolution of Remote Sensing Images[J]. Journal of Data Acquisition amp; Processing, 2008,23(2): 168-175. (in Chinese)

[4]Sondhi M M. Image Restoration: The Removal of Spatially Invariant Degradations[J]. Preceedings IEEE on Special Issue on Picture Processing. 1972, 60(7): 842-853.

[5]Andrews H C, Hunt B R. Digital Image Restoration[M]. Englewood Cliffs, New Jersey. USA: Prentice-Hall, 1977.

[6]洪汉玉, 张天序. 基于多分辨率盲目去卷积的气动光学效应退化图像复原算法[J]. 计算机学报. 2004, 27(7): 952-963.HONG Hanyu, ZHANG Tianxu. Investigation of Restoration Algorithm for Degraded Images Caused by Aero-optics Effects Using Multi-resolution Blind Deconvolution[J]. Chinese Journal of Computers. 2004, 27(7): 952-963. (in Chinese)

[7]Guan L, Ward R K. Restoration of Randomly Blurred Images by the Wiener Filter[J]. IEEE Transactions on Acoustics, Speech amp; Signal Processing, 1989, 37(7): 589-592.

[8]Hunt B R. The Application of Constrained Least Squares Estimations to Image Restoration by Digital Computer[J]. IEEE Transactions on Computer, 1973, 22(9): 805-812.

[9]陈强, 戴奇燕, 夏德深. 基于MTF理论的遥感图像复原[J]. 中国图像图形学报, 2006, 11(9): 1299-1305.CHEN Qiang, DAI Qiyan, XIA Deshen. Restoration of Remote Sensing Images Based on MTF Theory[J]. Journal of Image and Graphics, 2006, 11(9): 1299-1305. (in Chinese)

[10]秦世引, 魏晓明, 刘远民, 等. 模糊遥感图像总编分优化恢复方法[J]. 科技导报, 2011, 29(14): 26-32.QIN Shiyin, WEI Xiaoming, LIU Yuanmin, etal. A Restoration Method of Blurred Remote Sensing Images Based on Total Variation Optimization[J]. Science amp; Technology Review, 2011, 29(14): 26-32. (in Chinese).

[11]葛平, 王密, 潘俊, 等. 高分辨率TDI-CCD成像数据的自适应MTF图像复原处理研究[J]. 国土资源遥感, 2010, 87(4):23-28.GE Ping, WANG Mi, PAN Jun, etal. A Study of Adaptive MTF Restoration of High Resolution TDI-CCD Image Data[J].Remote Sensing for Land amp; Resources, 2010, 87(4): 23-28. (in Chinese)

[12]冈萨雷斯. 数字图像处理(第二版)[M]. 北京: 电子工业出版社, 2003: 75-77.Gonzales. Digital Image Processing(Second Edition) [M]. Beijing: Electronic Industry Press, 2003: 75-77. (in Chinese)

[13]刘正军, 王长耀, 骆成凤. CBERS-1 PSF估计与图像复原[J]. 遥感学报, 2004, 2(3): 234-238.LIU Zhengjun, WANG Changyao, LUO Chengfeng. Estimation of CBERS-1 Point Spread Function and Image Restoration [J].Journal of Remote Sensing, 2004, 2(3): 234-238. (in Chinese)

[14]周凯汀, 郑力新, 戴在平. 基于有限脉冲变换的FIR滤波器进化设计[J]. 华侨大学学报(自然科学版), 2001, 11(1): 81-84.ZHOU Kaiting, ZHENG Lixin, DAI Zaiping. Evolutionary Design of FIR Filter Based on Finite Impulse Transform [J].Journal of Huaqiao University (Natural Science), 2001, 11(1): 81-84. (in Chinese)

[15]仝云旭, 吴保卫. 连续时间线性脉冲系统的有限时间滤波[J]. 计算机工程与应用, 2014, 50(8): 48-52.TONG Yunxu, WU Baowei. Finite-time Filtering for Continue-time Linear Impulsive Systems [J]. Computer Engineering and Applications, 2014, 50(8): 48-52. (in Chinese)