基于FPGA的5/3提升小波优化算法

陈占良，金龙旭，陶宏江，韩双丽，张 敏

(1. 中国科学院长 春光学精密机械与物理研究所，吉林 长春 130033； 2.中国科学院大学，北京 100049)

基于FPGA的5/3提升小波优化算法

陈占良1，2，金龙旭1，陶宏江1，韩双丽1，张 敏1，2

(1. 中国科学院长 春光学精密机械与物理研究所，吉林 长春 130033； 2.中国科学院大学，北京 100049)

为了实现线阵CCD空间相机图像的实时压缩处理，在提升算法的基础上，提出了一种适用于FPGA的二维提升小波变换结构与实现方案。该系统利用FPGA片内的存储资源，采用乒乓操作实现了行列变换之间的数据缓存传输，降低了功耗，提高了硬件利用率和运算速度。并且为了适应硬件实现速度，在进行小波边界处理时不需要额外的边界延拓过程，很大程度上降低了算法的复杂度；整个模块采用verilog HDL语言进行设计，并在QuestaSim下进行了仿真试验。实验结果表明，该系统工作稳定可靠，完全满足实时处理的要求，并适用于JPEG2000的多级二维5/3小波变换。

实时压缩；提升算法；流水线结构；5/3小波变换；FPGA

离散小波变换是由Mallat提出的作为图像压缩的有效手段[1]，它是一种可以把信号分解为包括时间和频率信息的多种子带的变换，因此可以看作是一种多分辨率的信号处理方法[2]。在图像数据压缩中，离散小波变换使能量集中，并且在低比特率时能够实现更好的压缩效果[3-5]。

传统的小波变换都是通过卷积进行运算的，在此过程中需要复杂的加乘运算，硬件实现困难并且会耗费大量的寄存器资源。在提升算法的基础上提出的离散小波变换[6-7]有效地解决了传统小波变换的缺点，使小波变换的硬件实现成为可能，并且成为了图像压缩标准JPEG2000的基本算法[8-9]。本文在提升小波算法的基础上，基于流水线结构提出了一种多级5/3二维离散小波变换的FPGA实现方案。在遥感图像的实时处理过程中，线阵CCD空间相机采用推扫成像模式，所以CCD输出的图像格式是以行为单位实时输出的。本系统为了适应这种数据结构，并且达到实时处理的效果，提出了一种基于提升算法的二维小波变换结构，并且在ISE和QuestaSim下进行综合、仿真分析，达到了理想的运算速度和合理的资源利用。

1 提升小波变换算法原理

快速小波变换——Mallat算法是在多分辨率理论的基础上提出的，使小波分析理论得到了广泛的应用。Mallat算法如下

(1)

(2)

Mallat算法中存在大量的卷积运算，为了暂存中间结果，在硬件实现过程中就需要大量的存储单元，实现过程复杂。小波提升变换算法不依赖于傅里叶变换，从而不存在卷积运算，而是采用了预测、更新的方法来简化运算过程。在此过程中，复杂的卷积运算被简单的加减、移位运算代替，降低了计算量和复杂程度，运算效率提高了一倍，这都有利于硬件的实现和资源的节省。提升小波算法的实现包括分解(split)、预测(predict)、更新(update)3个步骤[10]，分别产生高频分量和低频分量。其中，高频分量表示图像的细节信息，低频分量表示图像背景等大尺度信息，提升小波变换结构如图1所示。

图1 提升小波变换

2 二维5/3提升小波变换的FPGA实现原理及系统结构

在5/3提升小波算法中以加减运算为主，伴有少量的除法运算，但也只是简单的除以2或者除以4的计算，在二进制的计算过程中右移一位或者两位即可，在硬件中移位运算很容易实现，因此采用FPGA来实现小波变换具有可行性。现在使用的高密度FPGA一般具有几万到几百万不等的门电路，以及丰富的EDA工具，为FPGA的开发、布局布线和综合仿真提供了充足的逻辑资源和良好的开发环境。

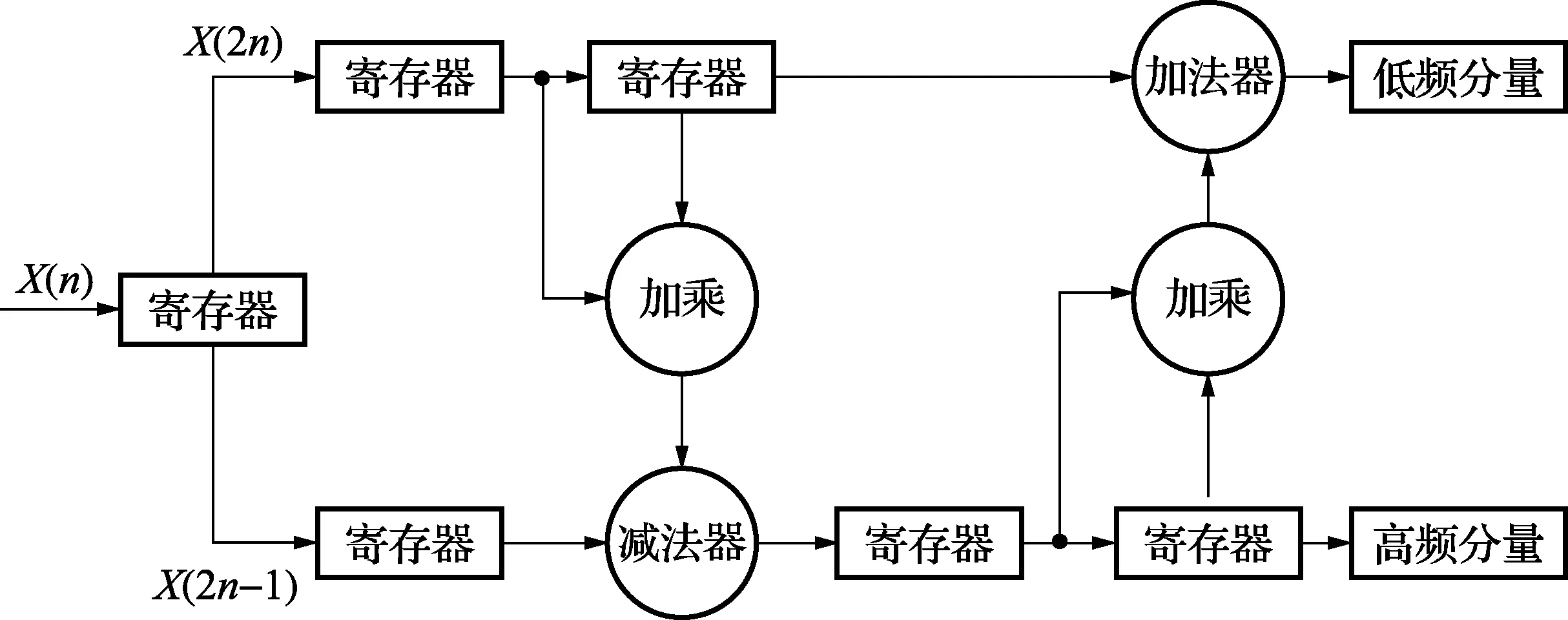
图3 串行流水线结构的提升小波变换电路结构

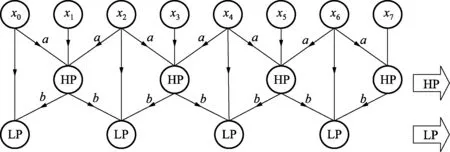
图4 一维5/3提升小波算法步骤

2.1 针对线阵CCD的二维离散小波变换实现方案

针对CCD是以行为单位输出图像的，为了达到图像的实时处理效果而不存在数据等待时间，提出了如图2所示的二维离散小波变换。该变换采用串行的流水线结构，一次可实现一级的二维小波变换。该结构包括小波变换模块和片内存储器模块，小波变换模块是对数据进行小波提升变换，片内存储器模块用来存储小波变换的中间结果。该小波变换分解得到4个子带频率，其中HH1、HL1、LH1用于后续的编码运算，而LL1直接输入下一级的小波变换中；输入到下一级的LL1频带数据当作行数据继续进行小波变换，得到的HH2、HL2和LH2同样用于后续的编码运算，而LL2输出作为下一级小波变换的数据。

图2 二维提升小波变换结构

依此循环进行，直到满足相应的小波级数要求[11]。这种结构数据流清晰，把主要精力放在数据的控制方面便可实现多级的二维小波变换结构。

2.2 5/3小波变换的边界处理

一维5/3提升小波变换的算法如下

(3)

(4)

小波变换公式的边界条件要求图像是无限长的输入序列，但是图像数据均由有限的行和列构成。在JPEG2000的标准协议的边界处理的方法是将数据周期对称延拓[12]，但是在对CCD产生的行数据进行实时处理时，周期对称延拓就意味着要产生多余的等待时间，在一定程度上会影响图像压缩的效率。因此，本文采用流水线的结构，严格控制数据路径，避免了对每行数据进行周期对称延拓，从而在一定程度上提高了运算速度。基于串行流水线结构的一维提升小波电路结构示意图如图3所示。根据行使能信号是否有效以及时序要求严格控制每个寄存器的数据传输，并且在适当的时序点使相应的寄存器数据为零，这样就有效地控制了边界数据的小波运算，而不必进行周期对称延拓边界数据，得到一维5/3小波提升步骤，如图4所示。

2.3 5/3提升小波变换的FPGA实现结构

要想进行小波变换，首先进作数据分解。数据分解的方式有很多种，最简单的就是采取奇、偶分解。对行数据进行数据分解的过程中，为了节省时钟资源和保证信号的同步性，本文放弃使用时钟分频单元对时钟信号进行分频、倍频操作，取而代之的是附加一个有效信号(valid)来决定寄存器数据的传输。这样既保证了多级小波变换信号间的同步性，同时以丰富的寄存器资源代替了片内有限的时钟资源，有利于片内资源的合理利用。

图3所示的电路结构可进行行提升小波变换。在行提升小波变换中，输入的CCD图像数据经过数据分解模块之后，得到的偶数序列和奇数序列同时输入到行小波变换模块中，在边界处理部分中，没有进行数据的周期对称延拓，而是选择了严格控制数据流，使用图4所示的小波提升算法步骤，避免了数据的等待时间，提高了运算速度。

由图2可知，列提升小波变换的输入是行提升小波变换结果的输出，本文采用的列提升小波变换的结构是以两行数据同时输入为基准，而行变换的输出为同步的高频和低频数据，且实际只是列变换中的一行数据。因此，在行变换与列变换之间用寄存器来缓冲数据，以此达到两行数据同时输出的效果。为了提高数据的处理速度，缓冲寄存器采用片内的块RAM结构来实现。本文采用3个线性RAM结构，以乒乓操作来实现数据的缓存传输，其结构示意如图5所示。

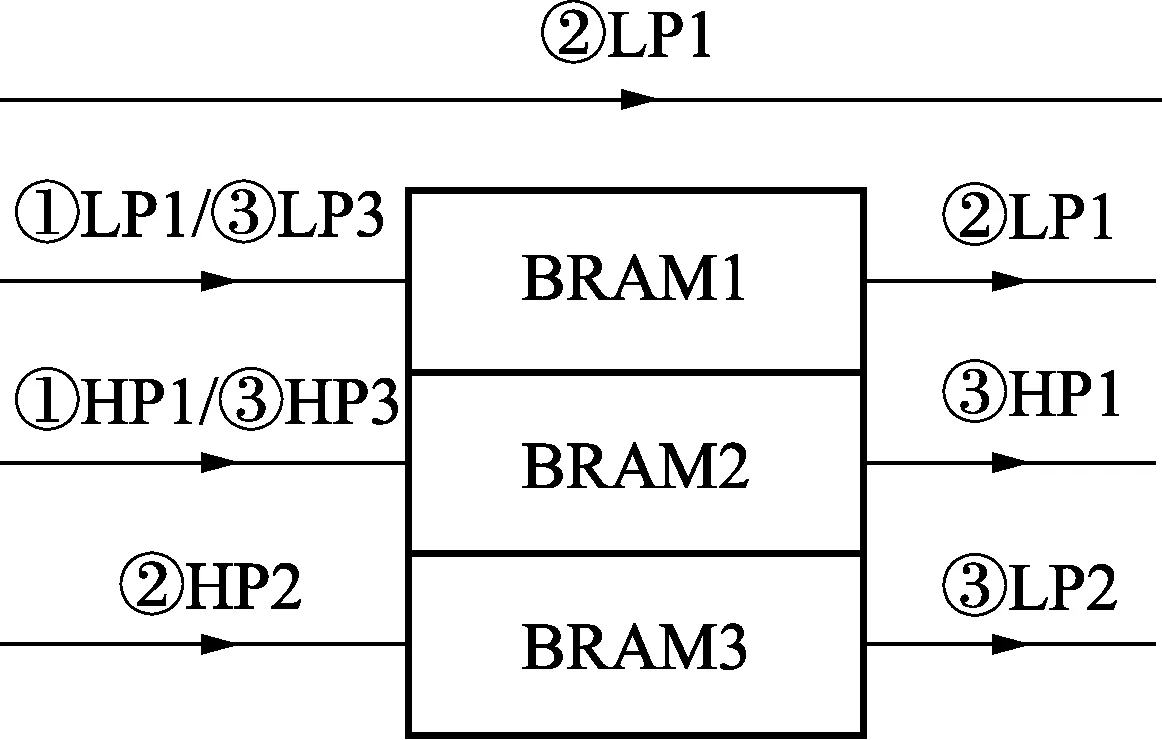
图5 数据缓存输出结构示意图

如图5所示，数据的缓冲输出分为3个阶段：

阶段①，由行变换产生的高频HP1、低频LP1信号分别缓存在BRAM1和BRAM2中。

阶段②，BRAM1输出阶段①中存储的低频信号LP1，同时BRAM3缓存行变换产生的高频信号HP2，行变换产生的低频信号LP2与LP1信号同时输出，构成两行数据中的前部分。

阶段③，BRAM2和BRAM3分别输出在阶段①和阶段②中缓存的高频信号HP1和HP2，与阶段②中的低频信号LP1和LP2共同组成完整的两行信号，此时下一行变换的高频HP3、低频LP3信号分别缓存在BRAM1和BRAM2中，此过程重复下去，直到完成数据缓存传输。

该缓存传输结构中用到的存储器是片内的块RAM，每个缓存器的长度为行数据的一半，利用乒乓操作，在速度与面积之间得到了很好的折中，合理利用了FPGA内部的寄存器资源。

列提升小波变换的算法步骤类似于图4所示，由于采用的是每次输入两行行数据，因此要完成列小波变换就需要等待其他行数据的输入，为此引入了缓存器用作缓存处理中间数据，本文提出的列提升小波变换电路结构如图6所示。

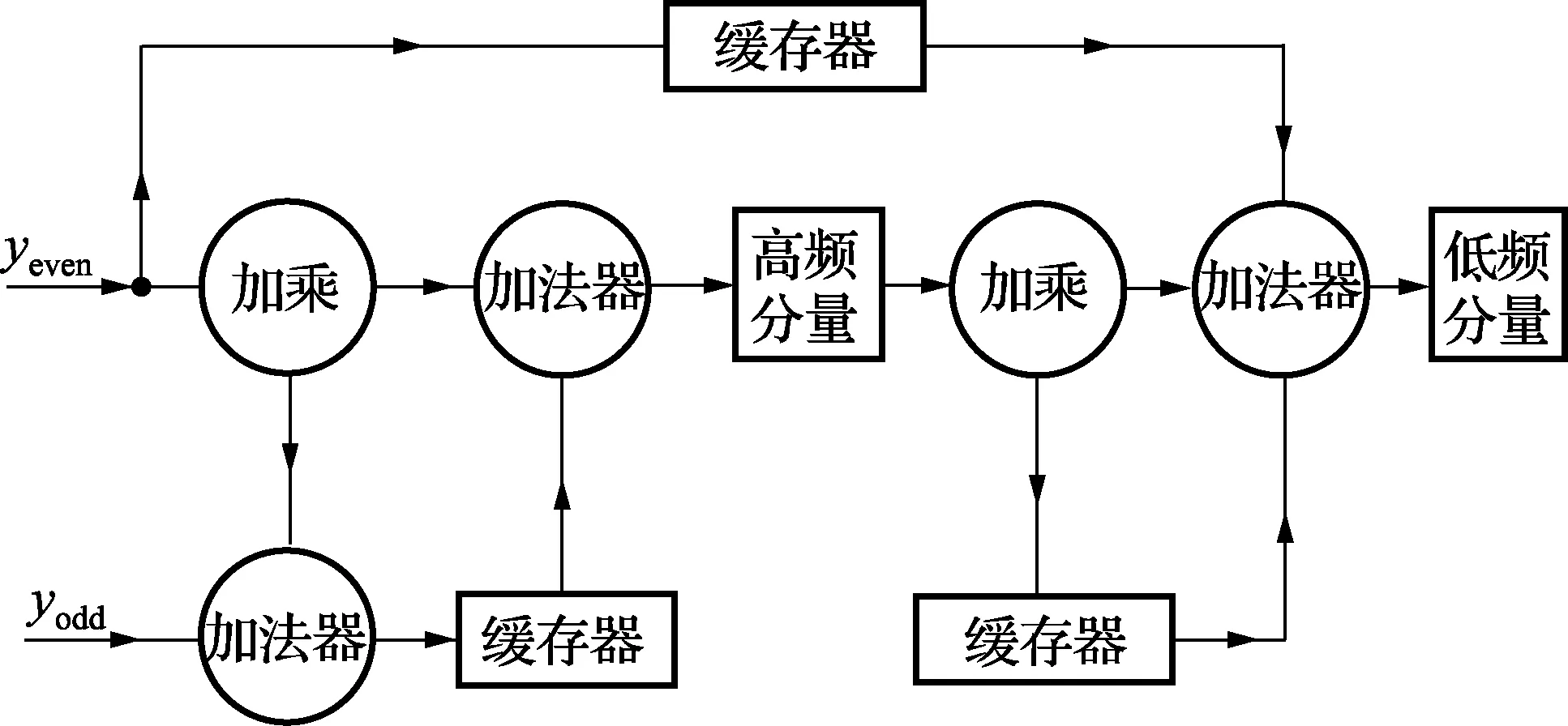
图6 列提升小波变换电路结构

3 仿真实验分析与结果

为了测试和仿真本算法的可行性，采用单行输入双行并行输出的格式信号在QuestaSim下仿真，图像数据大小为 16×16×16 bit，为了防止在运算过程中数据溢出，以及提高运算精度，在运算过程中采用20 bit的补码运算。采用本文提出的一级二维5/3小波变换结构进行时序仿真，得到的仿真波形如图7所示。

图7 二维小波变换仿真波形图(截图)

选用Xilinx公司的FPGA Spartan6系列的xc6slx45t-3，用ISE进行综合得到一级二维小波变换的最大时间频率为230 MHz，资源占用情况如表1所示。

表1 资源占用情况

为了实现五级小波变换，只需要将一级小波变换模块简单处理就能实现，并且在占用相同的逻辑资源的情况下使用的片内RAM为上一级的一半，减少了资源的使用量。

将本文提出的二维提升小波变换结构与文献 [13]提出的二维小波提升结构在使用资源和运算速度之间进行对比，如表2所示。从表中可以看出，当图像数据大小为256×256时，本文提出的结构所用的寄存器资源偏大，但当图像数据大小为512×512时，本文提出的结构所用的寄存器资源明显减少。主要是因为本文的图像像素大小是20 bit的定点数计算，而文献[13]的图像像素大小是13 bit，并且本文结构使用了更少的存储器资源。而且可以看出，本文提出结构的运算速度明显高于文献[13]的运算速度。

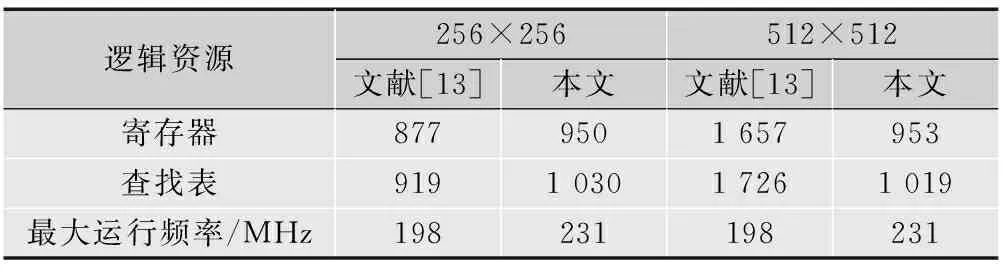
表2 使用资源和运算速度的对比

4 总结

本文讨论了用FPGA实现5/3提升小波变换的实现方法，根据线阵CCD成像的输出特点，提出了基于流水线的串行二维小波变换结构，适用于图像的实时处理过程。试验结果表明，提出的二维提升小波变换合理地解决了资源占用和运算速度的问题。本文只针对一级小波变换进行分析实验，但是多级变换仅仅是结构的复制与级联，因此本文提出的结构能够很好地实现多级小波变换，并适用于JPEG2000的多级二维5/3小波变换。

[1] MALLAT S. Theory for multiresolution signal decomposition： the wavelet representation[J]. IEEE Trans. Pattern Anal. and Machine Intel， 1989，11(7)：674-693.

[2] 刘平，王磊，郭中华，等. 基于小波变换的边缘保留图像去噪改进算法[J]. 电视技术，2014，38(5)：13-15.

[3] AZAWI S， BOUSSAKTA S， YAKOVLEV A. Performance improvement algorithms for colour image compression using DWT and multilevel block truncation coding[C]//Proc. 7th International Symposium on Communication Systems Networks and Digital Signal Processing (CSNDSP).[S.l.]：IEEE Press，2010：811-815.

[4] AL-AZAWI S， BOUSSAKTA S， YAKOVLEV A. Image compression algorithms using intensity based adaptive equantization coding[J]. American Journal of Engineeringand Applied Sciences， 2011(4)：504-512.

[5] AL-AZAWI S， BOUSSAKTA S， YAKOVLEV A. High precision and low power DCT architectures for image compression applications[C]//Proc. IET Conference on Image Processing (IPR). [S.l.]：IEEE Press，2012：1-6.

[6] DAUBECHIES I，SWELDENS W. Factoring wavelet transforminto lifting steps[J]. Fourier Analysis and Applications， 1998，4：247-269.

[7] 钟艳华. JPEG2000中DWT的VLSI结构设计[D]. 长沙：国防科学技术大学，2010.

[8] SKODRAS A， CHRISTOPOULOS C， EBRAHIMI T. The JPEG 2000 still image compression standard[J]. IEEE Signal Processing Magazine， 2001(18)：36-58.

[9] SKODRAS A N， CHRISTOPOULOS C A， EBRAHIMI T. JPEG2000： the upcoming still image compression standard[J]. Pattern Recognition Letters， 2001，22：1337-1345.

[10] 张立保，丘兵昌. 基于快速方向预测的高分辨率遥感影像压缩[J]. 光学精密工程，2013(8)：2095-2102.

[11] 王建军，刘波. 适于硬件实现的无损图像压缩[J].光学精密工程，2011(4)：922-928.

[12] TAN K C B， ARSLAN T. Low power embedded extension algorithm for lifting-based discrete wavelet transform in JPEG2000[J]. Electronics Letters， 2001， 37(22)： 1328-1330.

[13] AL-AZAWI S， ABBAS Y A ， JIDIN R. Low complexity multidimensional CDF 5/3 DWT architecture[C]//Proc. 9th International Symposium on Communication Systems Networks & Digital Sign (CSNDSP). [S.l.]：IEEE Press，2014：804-808.

陈占良(1990— )，硕士生，主研图像压缩和存储；

金龙旭(1965— )，博士，研究员，主研光电成像与图像处理；

陶宏江(1981— )，硕士，助理研究员，主研嵌入式系统和图像处理；

韩双丽(1968— )，女，副研究员，主研空间光学遥感器热控制技术；

张 敏(1990— )，女，博士生，主研光电成像与图像处理。

责任编辑：闫雯雯

Optimization Algorithm of 5/3 Lifting Wavelet Based on FPGA

CHEN Zhanliang1，2， JIN Longxu1，TAO Hongjiang1，HAN Shuangli1，ZHANG Min1，2

(1.ChangchunInstituteofOptics，FineMechanicsandPhysics，ChineseAcademyofSciences，Changchun130033，China；2.UniversityofChineseAcademyofSciences，Beijing100049，China)

In order to implement the real-time image data compression processing for line CCD space camera， a new method for lifting wavelet transform is proposed， which is based on the lifting algorithm structure. By using the abundant on-chip memories and ping-pong scheme， it can implement the data transmission between row transform and column transform. The method can reduce the power and enhance the speed of computation. It abandons the symmetric extension on the boundary， which can reduce the complexity of computation. The module is designed by verilog HDL， simulated by Questasim. The results indicate that the system can work steadily， and it is reasonable to implement real-time processing and multilevel 2-D 5/3 wavelet transform.

real-time compression； lifting algorithm； pipeline； 5/3 wavelet transform； FPGA

【本文献信息】陈占良，金龙旭，陶宏江,等.基于FPGA的5/3提升小波优化算法[J].电视技术,2015，39(11).

TP391

A

10.16280/j.videoe.2015.11.026

2015-01-06