基于变分模型的阵列三维SAR最优DEM重建方法

师 君张晓玲 韦顺军 向 高 杨建宇

(电子科技大学电子工程学院 成都 611731)

1 引言

阵列3维SAR[1－8]是指利用线型天线阵列代替传统合成孔径雷达的单天线结构，通过控制天线阵列的运动，合成2维等效阵列，并结合脉冲压缩技术获得3维空间分辨能力，以实现对观测目标3维成像的技术。与传统SAR相比，阵列3维SAR具有下视3维成像能力，在地形测绘、灾害监测等领域具有广泛的应用前景。

但是，由于阵列3维SAR需要在机翼上布设线阵天线以获得该方向的分辨率，载机平台尺寸限制使得其阵列方向分辨率远远低于距离向和航迹向。该缺陷严重制约了阵列3维SAR系统整体性能的提升。因此，需要针对阵列3维SAR数据特点，从成像/图像处理的角度研究提高阵列向分辨率的方法。

由于3维SAR图像显著的稀疏特性[9]，稀疏重建技术，如L1正则化方法，OMP，基追踪等技术目前已经被广泛用于层析SAR、圆周SAR、轨道3维SAR的成像处理，在提高图像分辨率、消除旁瓣等方面取得了一定的效果。但在深入研究后发现，直接将稀疏重建技术用于阵列3维SAR图像增强问题仍存在一些问题。

首先，稀疏特性并不能完全描述阵列3维SAR图像所具有的典型特征。在地形测绘任务中，目标散射点 3维空间中沿着某个特定的曲面(数字高程图/DEM)分布，图像增强应直接针对DEM图进行处理。而在采用稀疏重建技术时，DEM 图特有的“单值性”、“连续性”等特征被重述为“稀疏性”，实际上导致了约束条件的放松。单值性的缺失可能导致构造的高程图存在一个x,y位置对应多个高度的不合理情况，最终导致DEM提取误差。

其次，由于阵列3维SAR图像为3维数据，采用稀疏重建技术可能需要构造上亿维的线性方程组，并进行最优化求解，大大增加了算法的实现难度和可行性。而降维处理策略则会导致额外的模型误差，进一步影响DEM增强效果。

针对上述问题，本文讨论了基于变分模型的阵列3维SAR最优DEM重建方法，该方法直接将DEM 图作为最优化目标，通过寻找最优化 DEM图和对应的散射系数，实现最小二乘意义下的最优DEM重建。第2节简要回顾了阵列3维SAR的原理和成像处理方法，第3节对阵列3维SAR最优DEM重建的变分模型进行了分析讨论。第4节讨论了变分模型的求解方法，并提出了一种基于变分模型的阵列3维SAR最优DEM重建方法。第5节对该方法的性能进行了分析比较，验证了该方法的有效性。

2 阵列3维SAR原理

阵列3维SAR系统在机翼上安装线阵天线，通过阵列天线的相对运动合成2维虚拟面阵，以获得2维空间分辨率，并结合SAR雷达的距离分辨率实现对观测区域的3维成像，如图1所示。

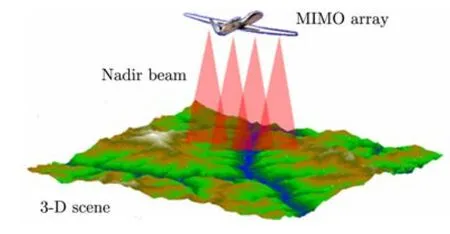
图1 阵列3维SAR工作几何Fig.1 Geometry of LASAR

阵列3维SAR的高度向分辨率由脉冲压缩技术获得，根据脉冲压缩理论，其分辨率为c/(2B)，其中，c为光速，B为发射信号带宽。阵列3维SAR的沿航迹向分辨率通过平台运动构成的合成孔径获得，根据合成孔径理论，其分辨率为λ/(2θ)，其中，λ为波长，θ为合成孔径角度。阵列 3维 SAR的切航迹向分辨率通过在机翼上布设阵列天线获得，其分辨率为 λR/(κA)，其中，R为雷达到目标的距离，A 为阵列长度，κ为常数，1＜κ＜2。假设雷达工作于Ka波段，阵列长度10 m，飞行高度10 km，则可得到系统阵列向分辨率约为4～8 m，远远低于距离向和航迹向分辨率。

在成像处理算法方面，由于阵列3维SAR的等效2维天线阵列结构复杂，RD算法、ωK算法适用性较差，无法满足任意模式3维SAR成像处理要求。因此，阵列3维SAR成像处理主要采用后向投影算法等时域处理技术。

采用后向投影算法进行成像处理后得到的3维SAR图像如图2所示，其中，x方向为阵列方向，y方向为平台运动方向，z方向为高度向。可以看出，其能反映出目标的典型几何特征。但是，观察其单个高度切片的图像可以看出，其图像在阵列方向分辨率较低，且由于稀疏阵列的采用，导致图像像素间的串扰较大。

3 最优DEM重建的变分模型

3.1 变分模型

在地形测绘任务中，阵列3维SAR主要观测目标为起伏地形，可写成散射系数与高程相对于水平面坐标系的函数的形式，即：

其中，x,y表示 2维水平面的变量，z(x,y)反映了x,y处地形的高度值，σ(x,y)反映了x,y处的复值散射系数。

假设阵列 3维 SAR系统的 3维模糊函数为χ(x,y,z)，则采用后向投影算法得到的成像结果可由高程函数z(x,y)和散射系数函数σ(x,y)表示为：

图2 阵列3维SAR成像处理结果Fig.2 Imaging results of LASAR

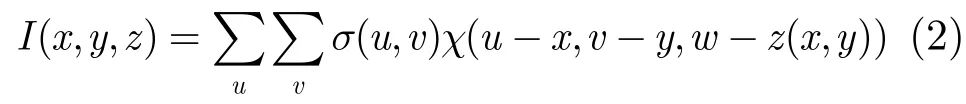
其中，u,v表示2维水平面的变量，I(x,y,z)表示利用系统模糊函数和散射系数估计得到的 3维 SAR图像。

利用式(2)和实际系统成像结果，可建立式(3)所示最优化问题模型：

其中，e(x,y,z)表示实际 3维图像与估计图像间的误差，表示实际系统得到的3维SAR图像。

式(3)表明，阵列3维SAR图像增强问题的可描述为针对z(x,y)和σ(x,y)的最优化问题：寻找高程函数z(x,y)和散射系数函数σ(x,y)，使得该高程函数和散射系数函数对应的估计结果与实际测量结果的误差最小。由于该最优化问题的优化变量为关于自由变量x和y的函数，其在数学上属于典型的变分问题。

为了便于分析与算法设计，需要进一步将3维模糊函数 χ(x,y,z)写成3个1维模糊函数乘积的形式，即：

其中，χR(⋅),χL(⋅)和χA(⋅)分别为距离向、阵列方向和航迹向的模糊函数。一般情况下，距离向和航迹向的系统分辨率优于或等于3维图像像素间隔，χR(⋅)和χA(⋅)可近似看作冲激函数，则式(2)可近似表示为：

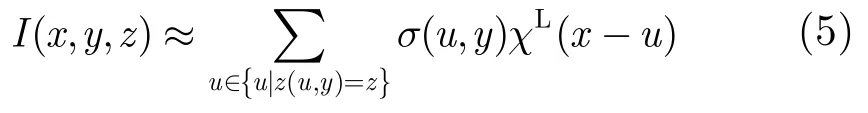
此时，式(3)的最优化问题可沿航迹向划分为一组相互独立的最优化问题：

其中，“/y”表示“给定航迹向距离单元y”，χ(x)=χL(x)。式(6)将二元变分优化问题转化为一组一元变分问题，大大降低了算法实现难度。

观察式(6)可以发现，一方面，由于最优化变量z(x)与模糊函数复合，该最优化问题属于典型的非线性变分，采用欧拉-拉格朗日方程法求解较为困难。另一方面，在z(x)已知条件下，关于散射系数σ(x,y)的最优化问题属于典型的最小二乘问题，可以采用伪逆、稀疏重建等方法进行求解。

因此，针对式(6)的最优化问题可分成两个阶段：首先，给定z(x)，求解最小二乘问题，得到对应的最优化散射系数和最优化代价函数值；其次，搜索所有可能z(x)，比较最优化代价函数值，选择最小的一个作为最优化z(x)其对应的最优化散射系数作为期望的散射系数。

3.2 局部化近似

为了降低求解该变分问题的难度，首先需要对其进行局部化近似处理，其核心是忽略阵列向模糊函数的旁瓣(在超分辨问题中，像素间隔远远小于阵列向分辨率，故散射点间的旁瓣串扰影响远远小于临近区域散射点间的主瓣串扰)。在此近似条件下，某个x位置处高度z和其对应的散射系数的改变只对其临近区域的数据产生影响，如图3所示。

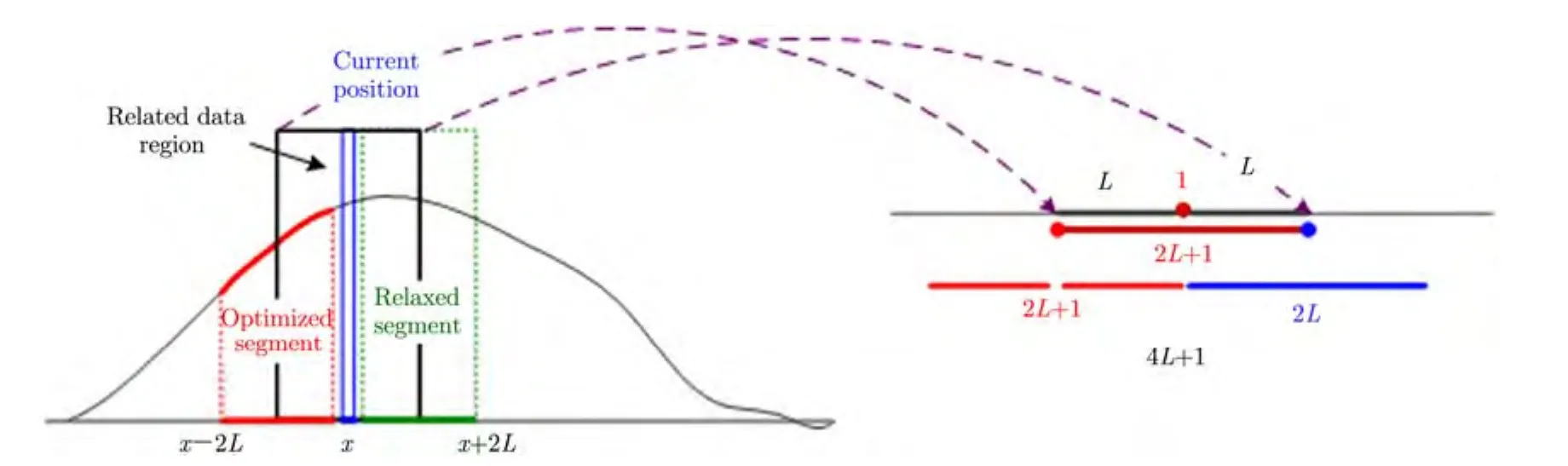
图3 DEM增强问题局部化Fig.3 Localization of the DEM enhancement problem

假设主瓣宽度为 2L+1，当前状态为 x，则改变当前位置的值将导致x−L到x+L段数据值(包含所有高度)发生改变。相应地，x−L到x+L数据段值的改变则会对x−2L到x+2L段散射系数产生影响。基于此特征，满足最优化问题式(6)的x处最优高度z，同样应满足式(7)所示最优化问题：

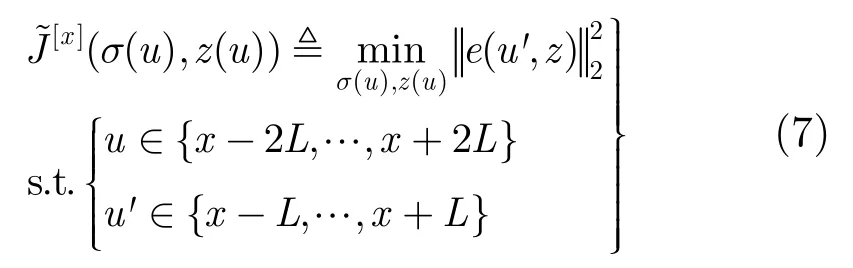
式(7)的物理意义为：寻找以x为中心的4L+1点最优路径使得以x为中心的2L+1点数据对应的均方误差最小。通过进一步分析可以发现，在无误差条件下，式(7)局部化问题的最优路径同样也是最优化问题式(6)的最优解。

为了便于计算最小二乘问题，需要通过数据重排技术，进一步将式(7)表示为矩阵形式，该过程可以通过简单的代数知识解决，此处不再赘述。当L=2时，给定高度h其对应的矩阵公式为：

需要注意的是，此处的散射系数σ(u,h)为 x-z切片内的散射系数，其为x和高度h的函数，而非式(1)中x与y的函数。此时，σ(u,h)具有稀疏性，即 ：σ(x,h)=0,h ≠ z(x)。 一 般 情 况 下 ，φ 为(2L+1)×(4L+1)矩阵，σ[h]为 4L+1 点列向量，d[h]为2L+1 点列向量。

对于整个2维相关数据段区域，其对应的矩阵表示为：

其中，Nz为3维图像沿z方向的像素点数。需要注意的是，根据其物理意义，σ只包含 4L+1 个非零分量。另外，如果事先已知σ的某些分量为0，则可以去除式(9b)中的对应行，以简化最小二乘问题。

4 基于OMP算法的变分模型求解

为了求解式(6)的全局最优化问题，需要消减其可行解集以达到降低运算量的目的。本文方法的基本策略是将全局最优化问题按照阵列方向分解为一系列的局部最优化问题，每个阶段只决定一个x位置对应的最优高度，并通过滑窗迭代的结构实现对整个x-z切片的最优化搜索。

通过观察可以发现，由于滑窗结构的采用，当优化x位置时，其先前位置的最优化高程已经获得，而无需进行重复搜索。另一方面，x位置的后续位置只用于估计当前局部最优化问题的最小均方误差，其各位置的高程将在后续迭代中计算，因此可以放松后续位置的“单值映射条件”。

基于上述考虑，式(7)可转化为改进的稀疏重建问题，即：

其中，第1个约束条件表示位置x−2L到x−1对应的高程为先前获得的最优化路径； Θ[x]为一个较大的复数，表示x状态处存在一个“显著的”散射系数；Sp(σ)表示σ的稀疏度，第3个约束条件表示整个优化问题的稀疏度为4L+1。

该最优化问题可以通过对OMP算法进行改进求解。第1个约束条件表明在进行OMP算法迭代初始，需要将x−2L 到x−1位置处已知高度对应于矩阵Ψ的指标集作为初始支撑集传递给OMP算法；第3个约束条件表明，OMP算法的迭代次数应为2L次(前 2L个高程已知，x处对应的高程需要遍历，在单次OMP调用时也相当于已知)。由于Θ[x]未知，且其取值随着x的变化而变化，第2个约束条件处理起来较为困难，本文采用式(11)估计式(10)的最优代价函数(详见附录)。

至此，基于OMP算法的变分模型求解算法如下：

目标：求解式(7)定义的局部最优化问题。

输入：给定矩阵Ψ，先前高程z(u)，观测数据d,L和当前状态x。

步骤1 高程遍历循环：遍历当前位置的所有可能高程，并进行如下操作：

(1) 选择z(x)，先前高程以及所有后续位置所对应的矩阵Ψ的行向量，获得Ψ的子矩阵；

(2) 记录z(x)和先前高程所对应的Ψ的子矩阵的行序号，作为OMP算法的初始支撑集；

(3) 调用OMP算法；

(4) 记录OMP算法的残留误差和z(x)对应的散射系数σ(z)。

步骤 2 寻找σ(z)的最大值，并利用式(11)计算J～[x](z)。

步骤 3 寻找J～[x](z)的最小值对应的位置作为当前位置x的最优高程。

输出：当前位置x的最优高程。

通过遍历所有沿阵列方向的位置x，即可得到当前x-z切片内的最优高程函数。

根据上述分析，基于OMP算法的变分模型求解方法的运算量为：

5 性能分析

由于超分辨率条件下图像增强问题属于典型的病态问题，其性能与信噪比密切相关。当无噪声条件下，很多算法都能获得较好的增强效果；但随着噪声的增加，不同算法的性能差异很大。本节仿真实验在固定超分辨倍数的条件下，分析不同算法的重建误差，并对基于变分模型的DEM重建算法的噪声性能进行分析比较。

仿真地形包括起伏山区地形和城市区域两种，图像尺寸为150像素×200像素。根据前面的分析可知，由于不同沿航迹单元内距离-阵列切片分的问题相互独立。本仿真也可以看作在相同信噪比条件下进行的不同地形200次蒙特卡洛实验。为了便于对比，标准的OMP算法[10－12]和LASSO算法[13－15]也被用于阵列3维SAR图像增强，其基本过程是抽取3维SAR图像中每个航迹向和距离向栅格的阵列向数据，调用稀疏重建方法得到处理结果，然后对选择每个水平面栅格节点处最大值作为该处高程的估计。

假设L=4，散射系数幅度为1(随机相位)，噪声标准差为0.1，变分模型方法、OMP和LASSO算法对起伏地形的处理结果如图4所示。对比可以看出，采用变分模型的处理方法可以在较大噪声条件下实现起伏地形的精确 DEM 增强，其对应的DEM残差图如图4(d)所示，其中只包含155个误差点。与之相比，OMP算法和LASSO算法所得到的处理结果则存在较大的噪声，其误差点分别为12691个和5926个。

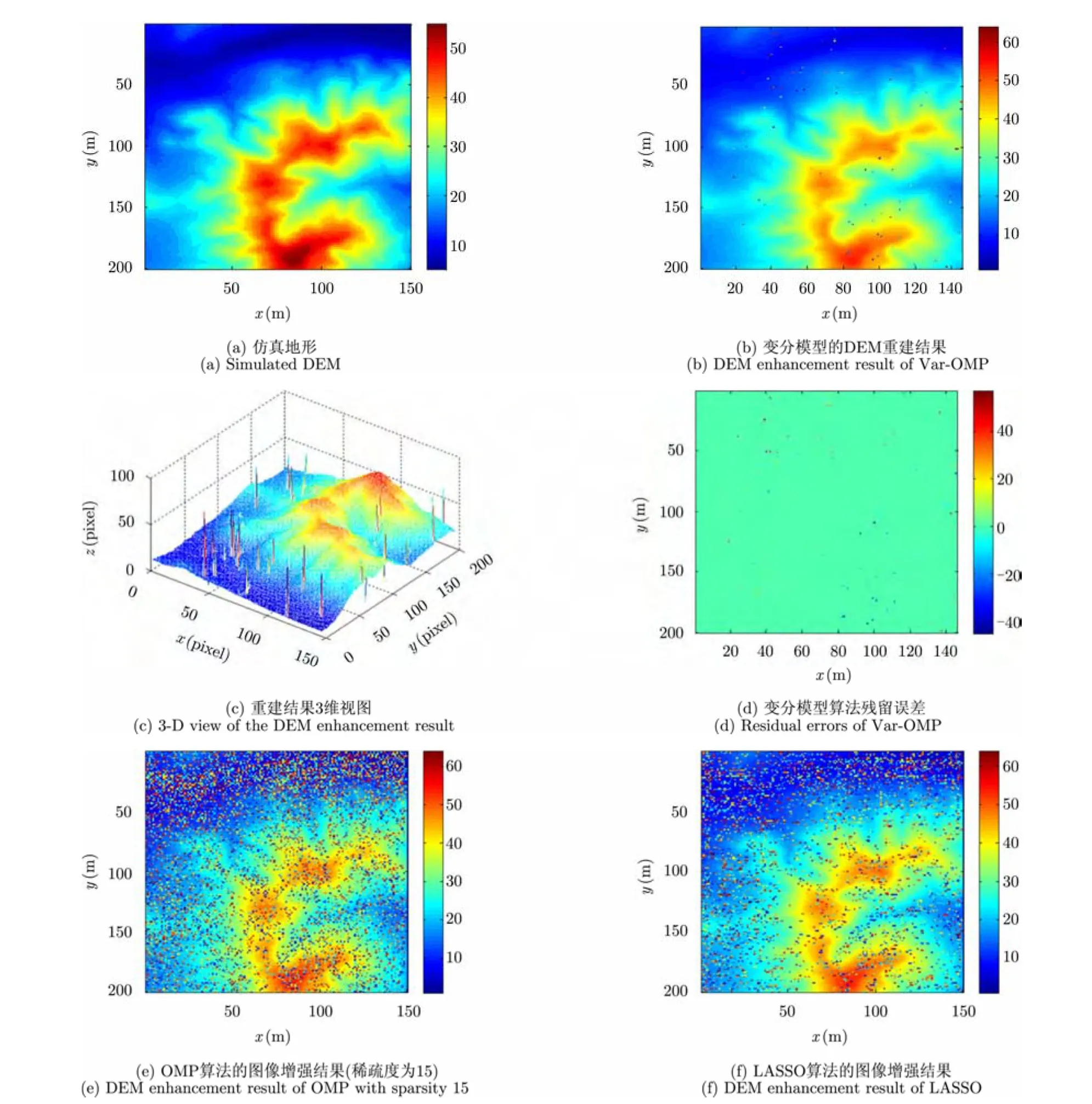
图4 起伏地形的最优DEM重建结果(L = 4，噪声标准差0.1)Fig.4 Enhancement results of a mountain area with L = 4 and the standard deviation 0.1

图5为仿真城市区域的DEM增强结果。观察图5(a)所示的观测地形可以发现，由于城市区域房顶等建筑结构与地面平行，其沿阵列方向抽取的数据表现出了“连续性”而非“稀疏性”。此时采用稀疏重建模型的算法处理将更为困难。图5(b)为变分模型的处理结果，可以看出其能够较好地重建城市区域地形。与之相反，图5(e)和图 5(f)的OMP算法、LASSO算法得到的结果则由于稀疏性的破坏导致处理效果严重下降。通过进一步统计发现，变分模型法、OMP和LASSO算法得到的DEM图像的残留误差分别为119,24473和14940。

通过上述分析比较可以看出，由于利用了DEM图的单值性特征，基于变分模型的DEM重建方法性能要远高于基于稀疏信号模型的重建方法，且在处理起伏地形、城市区域时都能得到较好的处理结果。

6 结论

本文提出了基于变分模型的阵列3维SAR最优DEM重建方法，该方法直接将DEM图作为最优化目标，通过寻找最优化DEM图和对应的散射系数，实现最小二乘意义下的最优DEM重建。仿真分析表明，该方法可以实现各种地形(山区、城市)等的稳健DEM增强，其性能远优于OMP算法和正则化方法。

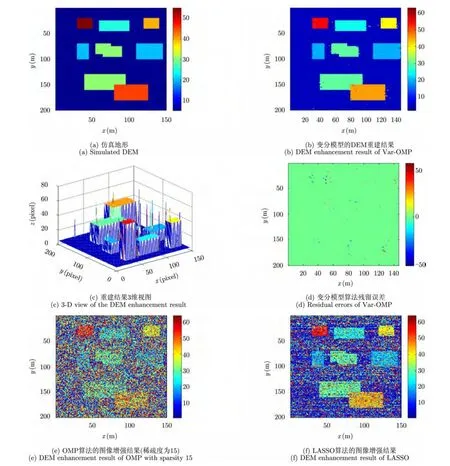
图5 城市区域的最优DEM重建结果(L = 4，噪声标准差0.1)Fig.5 Enhancement results of an urban area with L = 4 and the standard deviation 0.1

附录

本附录将推导式(11)，该问题可以重述为：

给定线性方程组Ax=y和其OMP算法解*x，计算该线性方程组在约束条件xi=c下的残留误差，其中，i属于支撑集。

为了分析上述问题，可将 OMP算法的残留误差写为：

另一方面，Ax=y且xi=c可以写为：

其中，A↓i表示剔除第i列后A矩阵的子矩阵，x↓i表示剔除第i个分量后x向量的子向量，αi表示矩阵A的第i列。

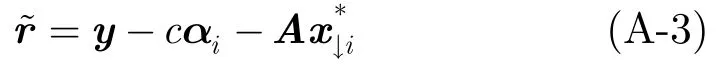
由于i属于支撑集，式(A-3)可表示为：

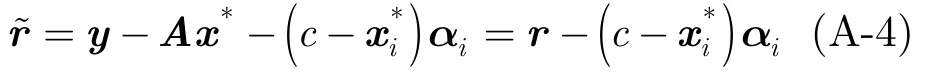
根据OMP算法的正交性，则有：

即式(11)。

[1]Matthias W and Markus G.Initial ARTINO radar experiments[C].20108th European Conference on Synthetic Aperture Radar (EUSAR),Aachen,Germany,2010: 1-4.

[2]Han Kuo-ye,Wang Yan-ping,Tan Wei-xian,et al..Efficient pseudopolarformat algorithm for down-looking linear-array SAR 3-D imaging[J].IEEE Geoscience and Remote Sensing Letters,2015,12(3): 572-576.

[3]Peng Xue-ming,Hong Wen,Wang Yan-ping,et al..Downward looking linear array 3D SAR sparse imaging with wave-front curvature compensation[C]. International Conference on Signal Processing,Communication and Computing (ICSPCC),Kunming,2013: 1-4.

[4]Zhang S,Zhu Y,and Kuang G.Imaging of downward-looking linear array three-dimensional SAR based on FFT-MUSIC[J].IEEE Geoscience and Remote Sensing Letters,2015,12(4):885-889.

[5]Peng Xue-ming,Hong Wen,Wang Yan-ping,et al..Polar format imaging algorithm with wave-front curvature phase error compensation for airborne DLSLA three-dimensional SAR[J].IEEE Geoscience and Remote Sensing Letters,2014,11(6): 1-5.

[6]Wei Shun-jun,Zhang Xiao-ling,and Shi Jun.Sparse autofocus via bayesian learning iterative maximum and applied for LASAR 3-D imaging[C].2014 IEEE Radar Conference,Cincinnat,USA,2014: 666-669.

[7]Zhang Ying-jie,Han Kuo-ye,Wang Yan-ping,et al..Study on motion compensation for airborne forward looking array SAR by time division multiplexing receiving[C].2013 Asia-Pacific Synthetic Aperture Radar (APSAR),Tsukuba,Japan,2013:392-395.

[8]Zhuge Xiao-dong and Yarovoy A G.A sparse aperture MIMO-SAR-Based UWB imaging system for concealed weapon detection[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(1): 509-518.

[9]Shi Jun,Zhang Xiao-ling,Xiang Gao,et al..Signal processing for microwave array imaging: TDC and sparse recovery[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(11): 4584-4598.

[10]Needell D and Tropp J A.CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3): 301-321.

[11]Wang Jian,Kwon S,and Shim B.Generalized orthogonal matching pursuit[J].IEEE Transactions on Signal Processing,2012,60(12): 6202-6216.

[12]Wang Jian and Shim B.On the recovery limit of sparse signals using orthogonal matching pursuit[J].IEEE Transactions on Signal Processing,2012,60(9): 4973-4976.

[13]Tibshirani R.Regression shrinkage and selection via the lasso[J].Journal Of The Royal Statistical Society Series B-Methodological,1996,58(1): 267-288.

[14]EfronB,Hastie T,Johnstone I,et al..Least angle regression[J].Annals of Statistics,2004,32(2): 407-499.

[15]Rosset S and Zhu Ji.Piecewise linear regularized solution paths[J].Annals of Statistics,2007,35(3): 1012-1030.