计及距离空间的电网参数误差支路选取方法

颜全椿，郑明忠，梁　伟（.江苏方天电力技术有限公司，江苏南京0；.江苏省电力公司电力科学研究院，江苏南京03）

计及距离空间的电网参数误差支路选取方法

颜全椿1，郑明忠2，梁伟2
（1.江苏方天电力技术有限公司，江苏南京211102；2.江苏省电力公司电力科学研究院，江苏南京211103）

电网参数错误将影响状态估计的质量，并降低能量管理系统中其它高级应用软件的实用化程序，研究实用的可疑支路集选取具有重要的现实意义。针对传统方法仅考虑本条支路量测残差的不足，提出计及相邻及外围支路残差的可疑支路选取方法。同时对不同支路距离的量测标准差加权处理，便于对不同运行工况及量测配置的支路可疑度进行排序比较；借助IEEE标准系统及某实际省网仿真计算的有效性，与传统可疑支路选取方法进行比较，结果表明该方法具有优越性。

输电网；距离空间法；可疑支路；参数辨识；状态估计

状态估计作为能量管理系统的核心与基石，其计算结果的准确与否直接影响电力系统状态估计、潮流计算、网损分析、暂态稳定和继电保护等高级应用软件的结果可靠性［1，2］。同时，随着智能电网的大力发展，调度自动化的要求越来越高，这就需要准确的电网参数模型［3-5］。传统状态估计一般假定电网参数及拓扑结构正确。实际中，由于参数录入错误、参数理论与现场实际值不对应、运行工况变化以及设备老化等原因，可能造成电网参数及拓扑结构的错误。目前，针对这一问题的2个主要方法是：（1）参数辨识［6-8］，即对含参数误差支路进行参数估计，并将模型参数进行修正，该方法仅需在平台中嵌入参数辨识模块，可以得到较接近真实值的参数；（2）现场参数实测［9-11］，该方法准确可靠，但费用人力物力具大。实际上，无论是参数辨识还是现场实测都没有必要对系统中所有参数进行验证，而参数误差支路的正确选取是重要前提。文献［12］基于拉格郎日乘子对可疑支路进行辨识，可同时计算出正则化量测残差和错误参数对应的拉格郎日乘子数值，数值稳定性好，但需重新计算验证参数辨识的可靠性。文献［13］对参数可估计性进行分析，提出主导与非主导参数的划分方法，并将非主导参数从可疑支路集中剔除，可提高程序稳定性，已在实际系统中得到应用。上述方法均只考虑支路本身的量测残差，而在状态估计中相邻与外围支路将相互影响，尤其对于含环网系统。为此，文中提出一种计及距离空间的可疑支路选取方法，仅需在原状态估计程序增加后续分析部分即可完成，具有良好的兼容性，仿真计算结果表明该方法在选取结果可靠性和计算速度方面均具有明显优势。

1　状态估计模型与求解

在给定拓扑结构、电网参数、量测数据的条件下，电力系统的量测方程为：

式中：z，h（x），v∈Rm×1分别为量测向量、量测函数向量、量测残差向量；x∈Rn×1为状态向量，除平衡节点外所有节点的电压实部与虚部；m，n分别为量测向量及状态向量的维数。

考虑不良数据及电网模型参数误差的存在，选取具有鲁棒性的抗差估计器［5］，其中，目前应用较广泛的是WLAV状态估计器，其模型为：

式中：zi，hi（x），vi分别为z，h（x），v向量的第i个元素。wi为Rm×1权重向最的第i个元素，一般可取1/σ2，σ2为对应量测数据的标准差。

利用内点法对WLAV模型进行求解。首先引入松弛变量l＞0，u＞0，l∈Rm，u∈Rm，即：

将式（2）的等式约束转化为障碍函数，构造相应的拉格郎日目标函数：

式中：y∈Rm，α∈Rm，β∈Rm为拉格朗日乘子，即对偶变量；l，u为原变量。式（4）的Karush-Kuhn-Tucker（KKT）最优条件为：

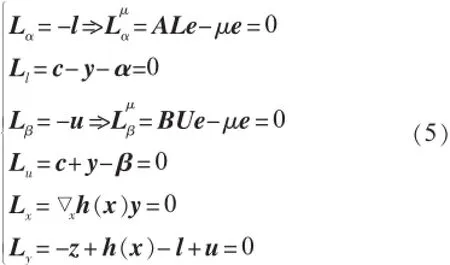
式中，△h（x）为h（x）的雅可比矩阵；μ为扰动因子；L，

x U，A，B分别为以l，u，α，β为对角元素的矩阵，e=［1，1，…，1］T。

将式（5）各式进行泰勒级数展开，并保留Ll与Lu的高阶项，得到：

式中：△2h（x）为h（x）的海森矩阵。

x

式（6—11）即为非线性高阶内点法的修正方程，并计算变量的迭代步长α：

式中：αp，αd分别为原、对偶变量的迭代步长，其目的是保证各变量满足大于零的条件，各变量修正方程为：

同时，定义内点法的互补间隙：

作为收敛判据（例如Cgap<10-6则算法收敛［5］），若不满足收敛条件，则修正扰动因子：

然后进行下一次迭代计算，直至算法满足收敛条件。式中，δ称为中心参数，一般取0.1，在大部分情况下能够获得比较好的收敛性。

2　计及距离空间的电网参数误差支路选取

2.1计及距离空间的可疑支路指标

以线路Li-j为例，说明距离空间法的可疑支路选取方法，如图1所示。数据采集与监控系统（SCADA）量测中主要包括首末节点注入有功、无功功率Pi，Qi及Pi，Qi，线路端有功、无功功率Pij，Qij、Pji，Qji。

在图1中，对线路Li-j其本体定义为距离1，赋权重0.7；相邻线路定义为距离2，赋权重0.2；外围线路定义为距离3，赋权重0.1。以线路对应量测的残差绝对值之和作为可疑支路的考核依据，考虑距离空间后Li-j的可疑指标为：

图1　距离空间法

式中：c=［0.7 0.2 0.1］为不同距离线路的权重向量；nbm为对应线路上所含量测数目；dj为相应距离的线路条数，即图1中Li-j的d2=4，d3=8。

由于各支路电压、功率的基准值及量测配置不同，对量测残差进行标准化，从而式（5）修正为：

式中：D=W-H（HTWH）-1HT为与残差灵敏度矩阵相关的对角阵。

2.2计及距离空间可疑支路选取方法

为了与实际现场的状态估计程序保持兼容性，文中的算法仅需要增加可疑指标计算。其中，量测标准化残差由状态估计模块接口输入，矩阵空间按如下方法实现：

（1）根据量测数据，对每个量测数据对应支路进行扫描，生成m×b维的量测-支路矩阵BM，b为电网总支路数目。若第i个量测对应支路为j，则BM（i，j）= 1，该行其余元素均为0；

（2）定义量测与支路距离为1的矩阵J1、距离为2的矩阵为J2、距离为3的矩阵为J3，即将式（18）转化为：

式中：，J1=I为单位矩阵；J2=BM；J3=f（J2×J2），函数f的作用为将矩阵中非零元置1，其余置0。由上述分析可知，对于距离k的矩阵获得方法如下：

综上，文中计及距离空间的参数误差支路选取方法实现流程如图2。

3　算例分析

3.1IEEE 30节点系统

用文中提出的方法对IEEE 30节点系统在Intel2.93 GHz的PC机上进行仿真试验。其中，试验用的量测生数据由潮流计算结果获得，所有的支路功率及节点注入功率、电压量测都配置齐全。传统WLS状态估计的收敛条件ε设为10-6。为了验证该方法对系统中含单一误差支路和多误差支路的选取有效性，距离空间的权重为c1=0.7，c2=0.2，c3=0.1。

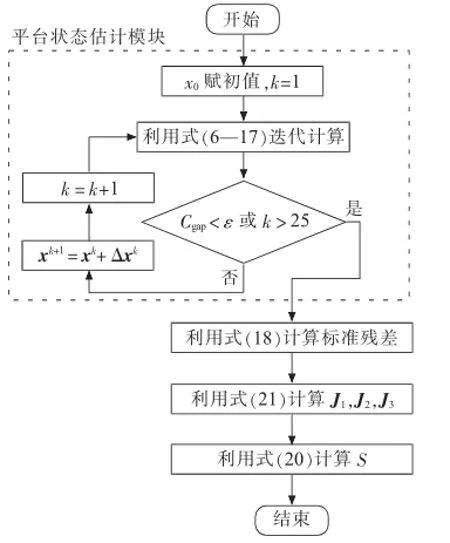
图2　计及距离空间的可疑支路选取流程

3.1.1单一误差支路选取

可疑支路选取的可靠性即受参数误差大小的影响又受量测误差的影响。为此，首先对无量测误差时，文中方法对单一误差支路的选取可靠性，对IEEE 30节点系统中线路L1-2（线路La-b表示由节点a到节点b的线路）的电抗改为原来的80%、120%、200%作为参数误差模拟，分别利用传统方法与本文方法进行辨识，S指标中最大3条支路见表1。

表1　无量测误差时单一误差支路选取结果

由表1可知，对于3种参数误差情况，传统方法可疑支路集中线路L1-3的S指标最大，对于该支路为错选，而含参数误差的线路线路L1-2仅排在第3，发生漏选。采用文中方法，3种情况下线路L1-2均排在第1位，表明成功选取出参数误差支路。

对量测生数据添加2%标准差的高斯白噪声作为量测误差，同样选取线路L1-2作为参数误差支路，不同方法的选取结果如表2。由表2可知，当含量测误差时，传统方法对线路L1-2的选取依然失败，不同的是此时线路L1-2在可疑度中排第2。而文中方法选取结果排序与不含量测误差时一致，表明该方法的运行结果是稳定且可靠的。

表2　含量测误差时单一误差支路选取结果

3.1.2多误差支路选取

对文中方法在多误差支路情况下的性能进行测试。随机选取L2-5、L4-12、L10-20、L25-27与L6-28共5条线路电抗增大50%作为参数误差支路，不同方法辨识的S指标最大5条线路如表3所示。

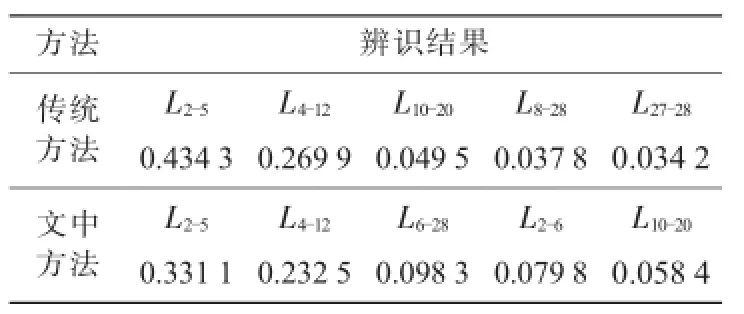
表3　多误差支路选取结果

由表3可知，传统方法成功辨识出线路L2-5、L4-12、L10-20，但误选了线路L8-28、L27-28，这是由于L6-28对其造成的影响。采用文中方法后，仅L25-27未排在前5可疑线路，这是由于L2-5对L2-6造成残差污染引起的，尽管如此，L25-27的S指标排在第7位，若在程序中设置恰当的门槛值，则以上5条参数误差支路都可成功辨识。

3.1.3量测配置对距离空间法的性能影响分析

文献［13］指出，电网参数可按其对状态估计的重要性可划分为主导参数与非主导参数，即若参数变化时对状态估计影响较大，则为主导参数，反之为非主导参数。在文中距离空间法的可疑支路选取中，由于可疑度指标同样基于状态估计残差进行计算，因此还无法较好地对非主导参数的误差进行辨识，但由于该参数对状态估计结果影响不大，不阻碍该算法的实用化。

此外，在试验过程中发现，该算法的可靠性与量测配置有关，尤其对于注入功率量测。为此，对IEEE 30节点系统中注入功率量测个数从0～3%选取7个样本进行单误差支路误差仿真测试，其辨识成功数如图3所示。由图3可知，当不含注入量测时，2种方法成功数相同，随着注入功率数目配置的增加，文中算法的成功数大幅提高，当满配置时，可达到26条，成功率为86.67%。

图3　不同量测配置时2种方法的辨识成功数比较

3.2实际省级电网

为验证文中方法对实际电网的可靠性，选取国内某实际省网进行测试分析，该电网含1119条母线、1992条线路（654条变压器支路），量测配置中包括：1118母线电压幅值量测、所有线路首末端功率量测（三绕组变压器不含末端量测）、789节点注入功率量测。在该省网调试平台的SCADA中随机选取2014年8月15日的10个断面数据作为测试样本，将S指标中排名前30的线路选入可疑支路集。由于参数辨识正确以否难于实际验证，利用文献［13］的方法对选取出的可疑支路进行WLAV参数估计，并以参数修正后该断面的状态估计合格率提出幅度作为参数辨识正确性的考核，2种方法的结果比较如表4所示。

表4　2种方法对实际省网的辨识结果比较

由表4可知，选取10个量测断面中，参数辨识前第5个断面合格率最低为97.231 9%，采用传统方法后状态估计合格率为98.916 5%，相比参数辨识前提高1.684 6%，而采用文中方法选取的可疑支路集并参数修正后，状态估计合格率可进一步提高至99.3867%，表明该方法较传统方法有更好的辨识效果，这与IEEE标准系统的测试结论是一致的。

4　结束语

针对传统可疑支路选取方法仅考虑本支路量测残差的不足，将相邻支路及外围支路进行综合评估，并利用加权平均对不同量测配置的支路进行排序比较。通过算例仿真验证了算法的有效性，该算法具有如下特点：（1）由于电网参数误差对状态估计的量测残差相互影响，计及距离空间的可疑支路选取结果具有更高的可靠性。（2）无论是单一误差还是多误差支路的选取均能够保证算法的稳定性，同时，该算法只需增加距离空间矩阵的计算即可得到可疑度指标，与原状态估计程序具有良好的兼容性。（3）电网模型中参数误差支路的选取方法仍处于不断发展中，计及距离空间可较为有效地选取出系统中所含的参数误差支路。同时，如何充分利用历史断面数据是下一步研究的重点。

［1］彭晖，赵家庆，王昌频，等.大型地区调度控制系统海量历史处理技术［J］.江苏电机工程，2014，33（5）：11-14，17.

［2］李云鹏，耿建，李会军，等.南通电网实时状态估计的工程化调试和应用［J］.江苏电机工程，2006，25（4）：30-32.

［3］颜全椿，卫志农，徐泰山，等.基于Gauss-Markov模型的电力系统t型抗差状态估计［J］.电力自动化设备，2014，34（6）：135-140.

［4］郭伟，单渊达.M估计及其在电力系统状态估计中的应用［J］.中国电机工程学报，2000，20（9）：26-31.

［5］颜全椿，卫志农，孙国强，等.基于多预测—校内点法的WLAV抗差状态估计［J］.电网技术，2013，37（8）：2194-2200.

［6］ZARCO P，EXPOSITO A G..Power System Parameter Estimation:a Survey［J］.IEEE Transactions on Power Systems，2000，15（1）：216-222.

［7］LIUWHE，WUFF，LIUSM.Estimation ofParameter Errorsform Measurement Residuals in State Estimation［J］.IEEE Transactions on Power Systems，1992，7（1）：81-89.

［8］王晓伟，蒋平，高磊，等.江苏电网电力系统稳定器参数辨识研究［J］.江苏电机工程，2007，26（2）：13-15.

［9］薛志英.输电线路工频参数在线测量方法的研究［D］.河北：华北电力大学（河北），2005.

［10］ZHU H.A Identification of Network Parameter Errors［J］.IEEE Transactions on Power Systems，2006，21（2）：586-592.

［11］柴京慧，李书敏，何桦.基于PMU及多时间断面的输电网参数估计［J］.电力系统自动化，2009，33（11）：49-52.

［12］周寅飞.基于内点法和离散粒子群算法的输电网参数辨识［J］.江苏电机工程，2014，33（1）：22-25.

［13］颜全椿，卫志农，徐泰山，等.基于主导与非主导参数的非线性加权最小绝对值参数估计［J］.电力系统自动化，2013，37（20）：71-76，126.

［14］SINGH H，ALVARADO F L.Weighted Least Absolute Value State Estimation Using Interior Point Methods［J］.IEEE Trans on Power Systems，1994，9（3）：1479-1484.

A Network Parameter Error Identification Method Considering Distance Space

YAN Quanchun1，ZHENG Mingzhong2，LIANG Wei2
（1.Jiangsu Frontier Electrical Power Technology Co.Ltd.，Nanjing 211102，China；2.Jiangsu Electric Power Company Electric Power Research Institute，Nanjing 211103，China）

Errors of network parameters can severely affect the performance of state estimation and degrade the usefulness of other advanced applications in an energy management systems（EMS）.It is important to develop a practical suspicious branch set selection method.Due to the deficiency of the traditional method which only considers the branch measurement residuals，a parameter error identification considering distance space is proposed，which takes the adjacent branch and peripheral branch into consideration.At the same time，the standards residual of different branch distance measurement are assigned with different weights，which facilitates the sorting comparison of different operation mode and measurement placement branch. Finally，the IEEE standard test system and a provincial power grid are adopted to verify the usefulness of the proposed approach，and the comparison results between the proposed method and the traditional parameter error identification method illustrate that the proposed method performances better.

transmission network；distance space；suspicious branch；parameter identification；state estimation

TM721

A

1009-0665（2015）05-0025-04

颜全椿（1989），男，福建三明人，硕士，从事电力系统状态估计、继电保护、电能质量研究工作；

郑明忠（1989），男，福建莆田人，硕士，从事电力系统运行分析与控制研究工作；

梁伟（1988），男，河南驻马店人，硕士，从事高压绝缘技术工作。

2015-04-18；

2015-06-02