水平井交替压裂裂缝间距优化及影响因素分析
2015-09-29杨兆中李小刚谢中成
杨兆中,苏 洲,2,李小刚,张 城,谢中成,邓 科
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都610500;2.中国石油塔里木油田分公司油气工程研究院,新疆库尔勒841000;3.中国石油川庆钻探股份有限公司塔里木工程公司,新疆库尔勒841000;4.中海石油(中国)有限公司上海分公司工程技术作业中心,上海200030;5.中国石油西南油气田分公司川东北气矿,四川达州635000)
讨论与争鸣
水平井交替压裂裂缝间距优化及影响因素分析
杨兆中1,苏洲1,2,李小刚1,张城3,谢中成4,邓科5
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都610500;2.中国石油塔里木油田分公司油气工程研究院,新疆库尔勒841000;3.中国石油川庆钻探股份有限公司塔里木工程公司,新疆库尔勒841000;4.中海石油(中国)有限公司上海分公司工程技术作业中心,上海200030;5.中国石油西南油气田分公司川东北气矿,四川达州635000)
为使水平井交替压裂在非常规油气储集层中形成大规模高效复杂体积缝网,需对交替压裂裂缝间距进行优化分析。从相邻2条压裂裂缝诱导应力叠加效应对初始水平主应力差的影响出发,建立了裂缝高度不同且缝内净压力也不同的物理模型,提出了交替压裂第一次压裂裂缝和第二次压裂裂缝临界裂缝间距及中间裂缝最佳起裂位置的确定方法。分析发现:前两次压裂裂缝临界裂缝间距随储集层岩石泊松比增大而减小,随裂缝高度和缝内净压力增大而增大;中间裂缝最佳起裂位置距第一次压裂裂缝的距离随储集层岩石泊松比增大而减小,随裂缝高度增大而增大,而缝内净压力对中间裂缝最佳起裂位置的影响较小。通过实例,将改进后的方法与已有方法进行对比分析后发现,改进后的临界裂缝间距和中间裂缝最佳起裂位置较已有方法能更准确地计算出诱导应力场,对非常规油气储集层交替压裂形成高效复杂体积缝网具有指导意义。
交替压裂;复杂体积缝网;应力干扰;叠加原理;裂缝间距优化
0 引言
页岩气与致密砂岩气等非常规油气储集层具有低孔隙度、极低渗透率特征[1-3],流体由储集层基质向裂缝中流动的阻力极大[4-6],使得常规压裂技术难以获得工业油气流,需进行体积压裂改造[7-12]。Soliman等[13-14]提出了以增大油气藏增产改造体积(Stimulated Reservoir Volume,简称SRV)为目的的交替压裂技术(Alternating Fracturing),也称作德州两步跳压裂技术(Texas Two-Step Method,简称TTSM),通过改变水平井分段压裂顺序,利用压裂裂缝产生的应力干扰作用实现非常规油气储集层体积压裂改造。Jo[15-16]通过数值计算方法对裂缝间距进行了优化分析,将前两次压裂裂缝诱导应力差(压裂裂缝在初始最小水平主应力和最大水平主应力方向上的诱导应力之差)分别达到最大值时的距离之和作为2条压裂主缝间的最优间距,但他忽略了超过最大诱导应力差后诱导应力叠加效应的影响,导致前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置均预测不准。邵尚奇等[17]在Jo[15-16]的基础上对水平井压裂裂缝间距进行了优化分析,但他忽略了裂缝诱导应力差最大值前端区域对诱导应力的影响。基于此,笔者利用弹性力学和水力压裂力学理论,分析裂缝诱导应力叠加效应对初始水平主应力差的影响,以期为裂缝间距分析及中间裂缝起裂位置确定均提供优化方法。
1 物理模型
1.1模型假设
为研究交替压裂前两次压裂裂缝间距对应力干扰作用的影响并确定中间裂缝最佳起裂位置,将储集层做如下假设:①储集层为均匀各向同性线弹性体,满足线性叠加原理;②压裂主裂缝近似为半无限裂缝,即裂缝长度大于或等于5倍裂缝高度[13,18];③储集层基质渗透率极低,每个压裂段结束后缝内净压力保持不变;④忽略弯曲裂缝效应,即第二次压裂裂缝的延伸不受第一次压裂裂缝诱导应力的影响。
1.2模型建立
常规压裂分析通常假定水力裂缝高度和缝内净压力均相同。但通过微地震监测和压裂压力拟合发现,水平井分段压裂裂缝高度和缝内净压力并非完全相同。为了优化分析水平井交替压裂前两次压裂裂缝间距及中间裂缝最佳起裂位置,以交替压裂一个作用单元为研究对象,建立了裂缝高度不同且缝内净压力也不同的物理模型(图1)。假定第一次压裂裂缝和第二次压裂裂缝高度分别为h1和h2,缝内净压力分别为pnet1和pnet2;前两次压裂裂缝间距为d,中间裂缝(第三次压裂裂缝)起裂位置距第一次压裂裂缝和第二次压裂裂缝的距离分别为d1和d2;最小水平主应力(σh)、最大水平主应力(σH)和垂向主应力(σv)的方向分别为x轴、y轴和z轴方向。

图1 交替压裂示意图Fig.1 Schematic of alternating fracturing
1.3单一裂缝诱导应力
Green等[19]提出了压裂裂缝产生的诱导应力计算解析式,并得出了水力压裂主裂缝在缝长、缝宽和缝高方向上的诱导应力分量计算表达式。根据上述物理模型基本假设可知,第一次压裂裂缝在初始最小水平主应力、垂向主应力和最大水平主应力方向上产生的诱导应力分量及水平方向上的诱导应力差[18]可分别表示为

式中:ν为储集层岩石泊松比;σx1,σy1与σz1分别为第一次压裂裂缝在缝宽、缝长和缝高方向上的诱导应力分量,MPa;ΔσFrac1为第一次压裂裂缝在水平方向上的诱导应力差,MPa。
当不考虑第一次压裂裂缝产生的诱导应力对第二次压裂裂缝延伸的影响时,根据储集层均匀各向同性假设及坐标变换原理,在第一次压裂裂缝和第二次压裂裂缝间距为d的情况下(坐标原点在第一次压裂裂缝中心处),第二次压裂裂缝在初始最小水平主应力、垂向主应力和最大水平主应力方向上产生的诱导应力分量及水平方向上的诱导应力差[19]可分别表示为
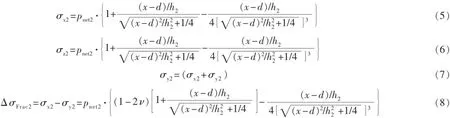
式中:σx2,σy2与σz2分别为第二次压裂裂缝在缝宽、缝长和缝高方向上的诱导应力分量,MPa;ΔσFrac2为第二次压裂裂缝在水平方向上的诱导应力差,MPa。
Jo[15-16]对式(4)求导,得到了前两次压裂裂缝诱导应力差达到最大值时裂缝间距的表达式,认为当2条裂缝诱导应力差分别达到最大时的距离之和,即为交替压裂前两次压裂裂缝的最优间距,可分别表示为
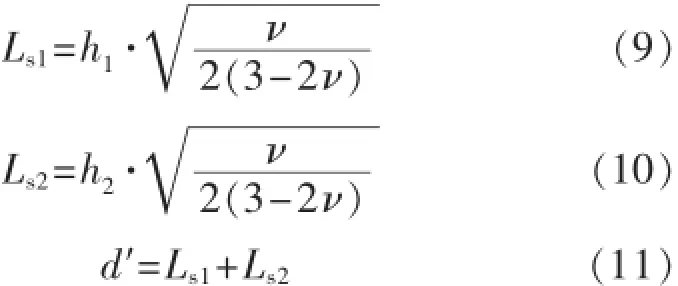
式中:Ls1与Ls2分别为第一次压裂裂缝和第二次压裂裂缝单独存在时,产生最大诱导应力差值所在点距第一次压裂裂缝和第二次压裂裂缝的距离,m;d′为利用Jo[15-16]法求得的前两次压裂裂缝最优裂缝间距,m。
1.4临界裂缝间距的确定
根据储集层均匀各向同性线弹性体假设可知,第一次压裂裂缝和第二次压裂裂缝之间区域总诱导应力差为这2条裂缝诱导应力差之和,即式(4)与式(8)计算结果之和,可表示为
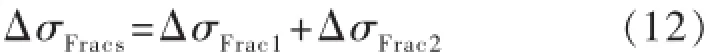
式中:ΔσFracs为第一次压裂裂缝和第二次压裂裂缝在水平方向上的总诱导应力差之和,MPa。
交替压裂前两次压裂裂缝间距不能过小,否则将使前两次压裂裂缝间的总诱导应力差大于初始水平主应力差,导致初始最大与最小水平主应力发生反转[13-14,20]。当在这2条裂缝之间进行第三次压裂时,将出现纵向裂缝,纵向裂缝的产生不仅不利于沟通前两次压裂诱导产生的应力松弛缝(Stressrelief Fractures),而且容易导致油气井发生早期砂堵。因此,有必要对交替压裂裂缝间距进行优化。
推荐采用图版法获取交替压裂前两次压裂裂缝临界裂缝间距。距离大于裂缝高度的1.5倍以后,诱导应力的影响将变得很小,可以忽略不计[21-24]。为进一步缩小裂缝间距搜索范围,建议从第一次压裂裂缝和第二次压裂裂缝高度之和(h1+h2)开始逐渐减小时,确定裂缝间距的临界值(dc)。
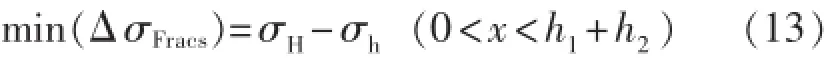
1.5中间裂缝最佳起裂位置的确定
由水力压裂力学理论可知,水力压裂主裂缝总是沿着垂直于最小主应力方向延伸。水平井交替压裂的核心理念是利用多级横向压裂裂缝之间的应力干扰作用,在储集层中形成纵横交错的复杂体积缝网。因此,产生与水平井井筒垂直的横向裂缝对体积缝网的形成至关重要。
为在储集层中形成多条横向主裂缝,需通过对前两次压裂裂缝间距进行优化,使中间裂缝起裂位置附近初始最大与最小水平主应力方向均不发生改变。当前两次压裂裂缝间距确定之后,诱导应力差取得最小值所在的位置即为中间裂缝最佳起裂位置。即

2 算例分析
利用表1所列的基本参数对交替压裂裂缝间距进行模拟分析。由式(1)~(4)可得到第一次压裂裂缝在初始最大水平主应力、最小水平主应力和垂向主应力方向上产生的诱导应力分量以及最小水平主应力与最大水平主应力方向上诱导应力之差[图2(a)]。从图2(a)可以看出,压裂裂缝在初始最小水平主应力方向上产生的诱导应力分量大于其在初始最大水平主应力方向上的诱导应力分量;同时,初始最小水平主应力与初始最大水平主应力方向上的诱导应力差(红色曲线)随离裂缝的距离增加先增大后减小,超过裂缝高度的1.5倍以后,诱导应力差较小。
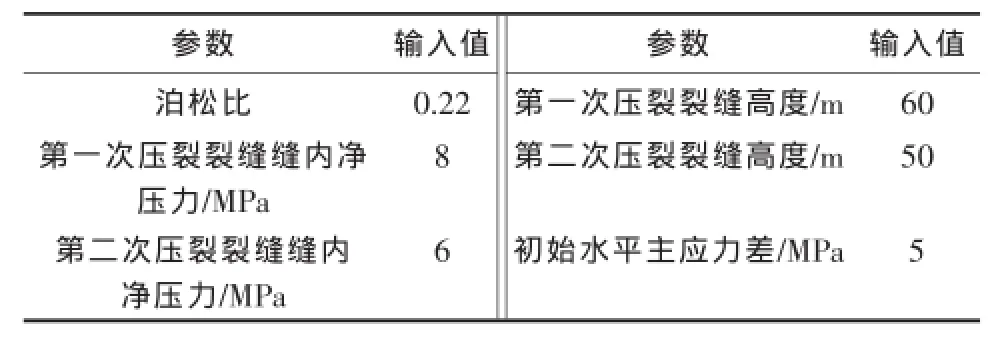
表1 基本模拟参数Table1 Basic simulation parameters
由垂直裂缝对称性可知,压裂裂缝在裂缝两侧各方向上产生的诱导应力分量同样具有对称性。为便于分析裂缝间诱导应力的叠加效应,首先考虑只有第二次压裂裂缝存在的情况,利用式(1)~(4)可得到第二条压裂裂缝在裂缝左侧产生的各方向上的诱导应力分量[图2(b)]。
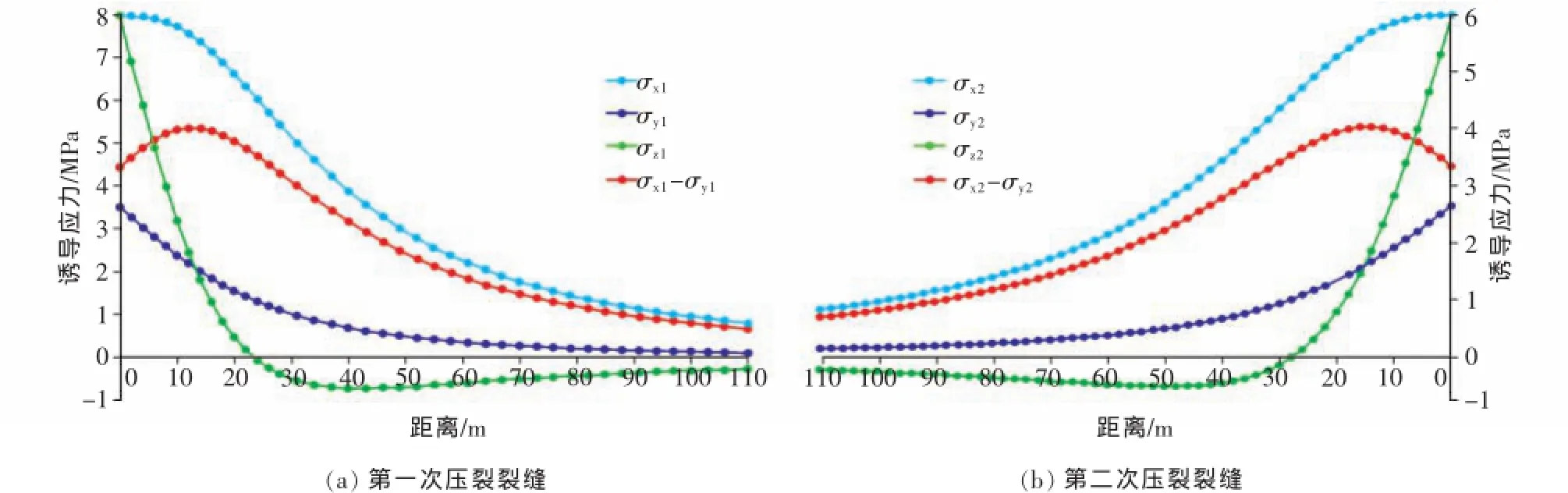
图2 压裂裂缝单独存在时的诱导应力Fig.2 Induced stress caused by one hydraulic fracture alone
根据弹性力学理论,前两次压裂裂缝之间区域总诱导应力可表示为第一次压裂裂缝和第二次压裂裂缝诱导应力差之和。裂缝间距从第一次压裂裂缝与第二次压裂裂缝的高度之和开始逐渐减小时进行搜索,当搜索至接近临界裂缝间距时,减小搜索步长,以便快速找到临界间距。利用式(13)可确定临界裂缝间距,即2条裂缝诱导应力差之和的最小值使得初始最大水平应力与最小水平主应力发生反转的临界条件(图3)。
从图3可以看出,随着裂缝间距减小,叠加后的诱导应力差逐渐增大,且随着裂缝间距进一步减小,叠加后的诱导应力差增大幅度逐渐增大。为保证第三次压裂产生横向裂缝,压裂设计时应使前两次压裂裂缝间距大于临界裂缝间距;另外,为了降低第三次压裂施工净压力并更好地形成体积缝网,裂缝间距不宜过大。图3中临界裂缝间距为81 m,当裂缝间距小于81 m时,前两次压裂裂缝之间所有区域应力都将发生反转,在进行第三次压裂时将出现纵向裂缝,不利于体积缝网的形成;当裂缝间距大于83 m时,形成同等规模的复杂体积缝网需要更大的缝内净压力,对地面和井下设备均提出了更高的要求。因此,为保证第三次压裂裂缝为垂直于井筒的横向裂缝,同时,减小缝内净压力要求,建议交替压裂前两次压裂裂缝间距取83 m。另外,根据式(14)计算得出,中间压裂裂缝最佳起裂位置距第一次压裂裂缝的距离为45.9 m。
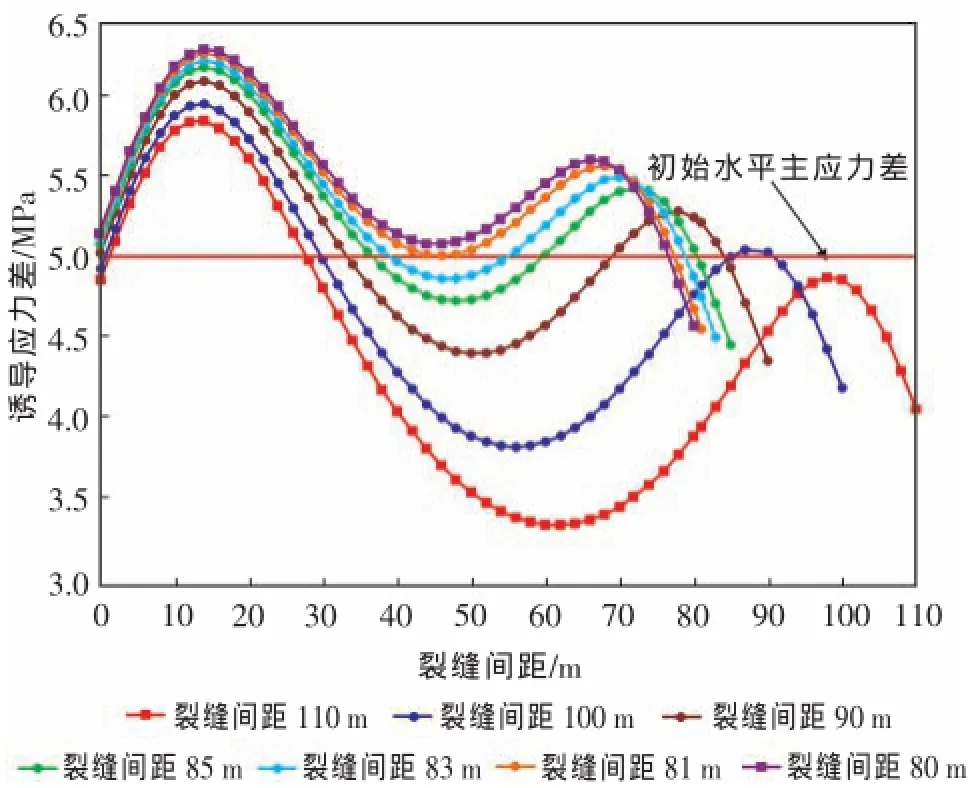
图3 不同裂缝间距下的诱导应力差Fig.3 Induced stress changes caused by different fracture spacing between the first and second hydraulic fracture
根据Jo[15-16]提出的裂缝间距优化计算表达式[式(9)~(11)]及模拟参数(参见表1),计算得出第一次压裂裂缝诱导应力差在距离裂缝12.44 m处达到最大,最大诱导应力差为5.38 MPa;同理,第二次压裂裂缝诱导应力差在距离裂缝10.36 m处达到最大,最大诱导应力差为4.03 MPa。由此可得出,前两次压裂裂缝最优间距为22.8 m,中间裂缝起裂位置距第一次压裂裂缝和第二次压裂裂缝的距离分别为12.44 m和10.36 m。Jo[15-16]方法和改进后的方法对比结果如图4所示。
从图4可以看出,利用Jo[15-16]方法得到的裂缝间距将使前两次压裂裂缝之间所有区域诱导应力差远远大于初始水平主应力差,导致初始最大主应力与最小主应力方向完全反转。这样在这2条裂缝之间的任意位置进行压裂施工都将出现纵向裂缝,严重阻碍了复杂体积缝网的形成,甚至导致早期砂堵。另外,从经济角度来看,Jo[15-16]方法得到的结果也不利于油气田开发推广使用。改进后的方法结果更优,2条压裂裂缝之间除中间裂缝起裂位置附近以外,其他区域地应力均发生了反转,一方面能够保证中间裂缝为与水平井筒垂直的横向裂缝,另一方面能够更好地产生转向分支缝,与前两次压裂形成的应力释放裂缝相连通。因此,改进后的方法更有利于交替压裂形成复杂体积缝网。

图4 Jo方法与改进后方法结果对比Fig.4 Comparison of results between method proposed by Jo and existed optimizing method
3 影响因素分析
根据Green等[19]提出的水力压裂垂直裂缝沿3个主应力方向上产生的诱导应力分量计算解析式和应力叠加原理可知,影响前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置的因素主要包括储集层岩石泊松比、第一次压裂裂缝高度和缝内净压力以及第二次压裂裂缝高度和缝内净压力。由前两次压裂裂缝对称性分析可知,只需要研究储集层岩石泊松比及其中任意一次压裂裂缝参数(裂缝高度和缝内净压力)的变化对前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置的影响。
3.1储集层岩石泊松比的影响
图5为储集层岩石泊松比对交替压裂前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置(图中指中间裂缝起裂位置距第一次压裂裂缝的距离,下同)的影响。从图5可以看出,随着泊松比增大,前两次压裂裂缝临界裂缝间距逐渐减小,中间裂缝起裂位置距第一次压裂裂缝的距离也逐渐减小。这是由于在其他参数一定的情况下,泊松比越大,压裂主裂缝产生的诱导应力沿缝长方向上的分量越大,对储集层初始水平主应力差的改变越小。要实现同等程度的应力改变,就需要更小的裂缝间距以增强裂缝间应力的干扰作用,同时,中间裂缝起裂位置也相应地向第一次压裂裂缝靠近。
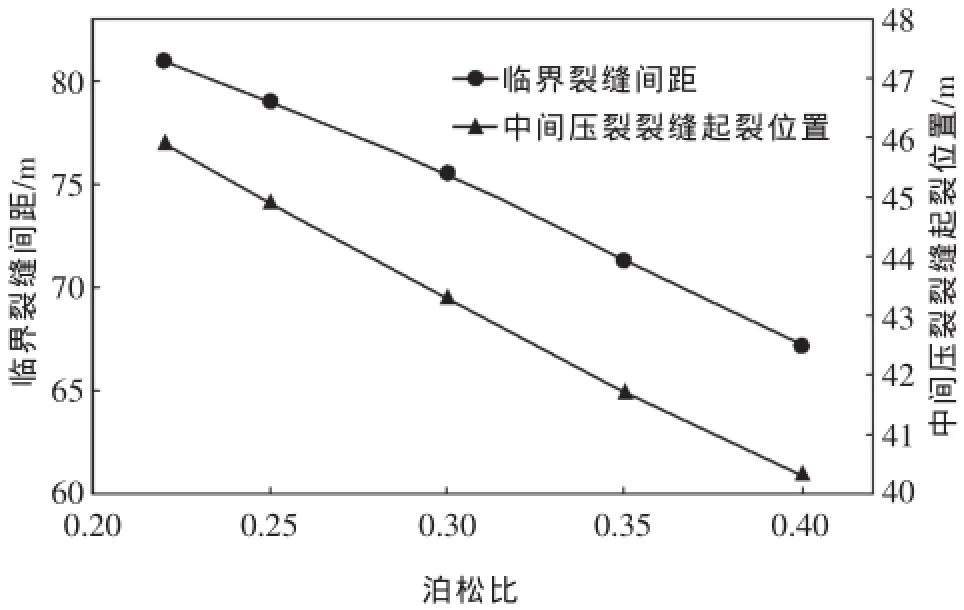
图5 储集层岩石泊松比对临界裂缝间距和中间裂缝最佳起裂位置的影响Fig.5 Effect of Poisson's ratio on critical fracture spacing between the first and second hydraulic fracture and optimal initiation position for the third one
3.2第二次压裂裂缝高度的影响
图6为在表1中其他参数不变的情况下,第二次压裂裂缝高度对交替压裂前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置的影响。从图6可以看出,第二次压裂裂缝高度越大,则前两次压裂裂缝临界裂缝间距越大,中间裂缝最佳起裂位置距第一次压裂裂缝的距离越远。第二次压裂裂缝高度每增加10 m,前两次压裂裂缝临界裂缝间距将增大约6.8 m,中间裂缝最佳起裂位置距第一次压裂裂缝的距离将增大3.2 m。由此可见,第二次压裂裂缝高度对交替压裂前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置的影响均较显著。
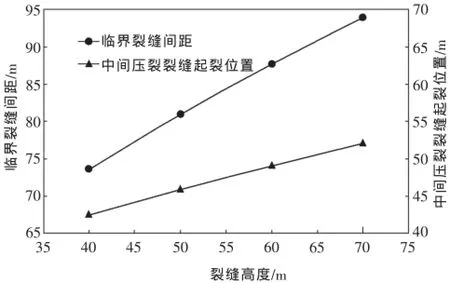
图6 裂缝高度对临界裂缝间距和中间裂缝最佳起裂位置的影响Fig.6 Effect of fracture height on critical fracture spacing between the first and second hydraulic fracture and optimal initiation position for the third one
3.3第二次压裂裂缝缝内净压力的影响
根据水力压裂主裂缝诱导应力差解析式[式(4)和式(8)]可知,缝内净压力是交替压裂应力干扰作用的重要影响因素之一。图7为交替压裂第二次压裂裂缝缝内净压力对前两次压裂裂缝临界裂缝间距和中间裂缝最佳起裂位置的影响。从图7可以看出,第二次压裂裂缝缝内净压力越大,前两次压裂裂缝临界裂缝间距越大,中间裂缝最佳起裂位置距第一次压裂裂缝的距离越远。值得注意的是,第二次压裂裂缝缝内净压力对中间裂缝最佳起裂位置影响较小,这是由于前两次压裂裂缝临界裂缝间距的增加与第二次压裂裂缝缝内净压力的增大基本持平,使得中间裂缝最佳起裂位置基本保持不变。

图7 缝内净压力对临界裂缝间距和中间裂缝最佳起裂位置的影响Fig.7 Effect of net fracture pressure on critical fracture spacing between the first and second hydraulic fracture and optimal initiation position for the third one
4 结论
(1)适当程度的应力干扰是水平井交替压裂实现非常规油气储集层体积缝网压裂改造的关键。
(2)交替压裂前两次压裂裂缝间距对应力干扰的影响十分显著,过小的裂缝间距将导致第三次压裂裂缝为纵向裂缝,不利于复杂体积缝网的形成,甚至导致早期砂堵;过大的裂缝间距对形成同等复杂程度体积缝网的井下和地面设备均要求更高。
(3)储集层岩石泊松比越大,则前两次压裂裂缝临界裂缝间距越小,且中间裂缝最佳起裂位置距第一次压裂裂缝越近;裂缝高度越大或缝内净压力越大,则前两次压裂裂缝临界裂缝间距越大,且中间裂缝最佳起裂位置距第一次压裂裂缝越远。
(4)由改进后的临界裂缝间距和中间裂缝起裂位置计算得到的裂缝诱导应力更精确,更有利于水平井交替压裂实现油气藏复杂体积缝网压裂改造。
(References):
[1]祝彦贺,胡前泽,陈桂华,等.北美A-29区块页岩油资源潜力分析[J].岩性油气藏,2013,25(3):66-70.
Zhu Yanhe,Hu Qianze,Chen Guihua,et al.Study on resource potential of shale oil in A-29 Block,North America[J].Lithologic Reservoirs,2013,25(3):66-70.
[2]王民,石蕾,王文广,等.中美页岩油、致密油发育的地球化学特征对比[J].岩性油气藏,2014,26(3):67-73.
Wang Min,Shi Lei,Wang Wenguang,et al.Comparative study on geochemical characteristics of shale oil between China and U.S.A[J].Lithologic Reservoirs,2014,26(3):67-73.
[3]李传亮,朱苏阳.页岩气其实是自由气[J].岩性油气藏,2013,25(1):1-3.
Li Chuanliang,Zhu Suyang.Shale gas is free gas underground[J]. Lithologic Reservoirs,2013,25(1):1-3.
[4]邹才能,杨智,张国生,等.常规-非常规油气“有序聚集”理论认识及实践意义[J].石油勘探与开发,2014,41(1):14-27.
Zou Caineng,Yang Zhi,Zhang Guosheng,et al.Conventional and unconventional petroleum“orderly accumulation”:Concept and practical significance[J].Petroleum Exploration and Development,2014,41(1):14-27.
[5]林森虎,邹才能,袁选俊,等.美国致密油开发现状及启示[J].岩性油气藏,2011,23(4):25-30.
Lin Senhu,Zou Caineng,Yuan Xuanjun,et al.Status quo of tight oil exploration in the United States and its implication[J].Lithologic Reservoirs,2011,23(4):25-30.
[6]黄籍中.四川盆地页岩气与煤层气勘探前景分析[J].岩性油气藏,2009,21(2):116-120.
Huang Jizhong.Exploration prospect of shale gas and coal-bed methane in Sichuan Basin[J].Lithologic Reservoirs,2009,21(2):116-120.
[7]Mayerhofer M J,Lolon E P,Warpinski N R,et al.What is stimulated reservoir volume?[R].SPE 119890,2010:89-98.
[8]Soliman M Y,Loyd E,Adams D.Geomechanics aspects of multiple fracturing of horizontal and vertical wells[R].SPE 86992,2008:217-228.
[9]吴奇,胥云,王晓泉,等.非常规油气藏体积改造技术——内涵、优化设计与实现[J].石油勘探与开发,2012,39(3):352-358.
Wu Qi,Xu Yun,Wang Xiaoquan,et al.Volume fracturing technology of unconventional reservoirs:Connotation,optimization design and implementation[J].Petroleum Exploration and Development,2012,39(3):352-358.
[10]吴奇,胥云,王腾飞,等.增产改造理念的重大变革——体积改造技术概论[J].天然气工业,2011,31(4):7-12.
Wu Qi,Xu Yun,Wang Tengfei,et al.The revolution of reservoir stimulation:An introduction of volume fracturing[J].Natural Gas Industry,2011,31(4):7-12.
[11]吴奇,胥云,刘玉章,等.美国页岩气体积改造技术现状及对我国的启示[J].石油钻采工艺,2011,33(2):1-7.
Wu Qi,Xu Yun,Liu Yuzhang,et al.The current situation of stimulated reservoir volume for shale in U.S.and its inspiration to China[J].Oil Drilling&Production Technology,2011,33(2):1-7.
[12]张小龙,张同伟,李艳芳,等.页岩气勘探和开发进展综述[J].岩性油气藏,2013,25(2):116-122.
ZhangXiaolong,ZhangTongwei,LiYanfang,etal.Researchadvance in exploration and development of shale gas[J].Lithologic Reservoirs,2013,25(2):116-122.
[13]Soliman M Y,East L,Augustine J.Fracturing design aimed at enhancing fracture complexity[R].SPE 130043,2010:1-20.
[14]East L,Soliman M Y,Augustine J.Methods for enhancing far-field complexity in fracturing operations[R].SPE 133380,2010:1-17.
[15]Jo H.Optimizing fracture spacing to induce complex fractures in a hydraulicallyfracturedhorizontalwellbore[R].SPE154930,2012:1-14.
[16]Jo H.Optimal fracture spacing of a hydraulically fractured horizontal wellbore to induce complex fractures in a reservoir under high in-situ stress anisotropy[R].IPTC 16717,2013:1-12.
[17]邵尚奇,田守嶒,李根生,等.水平井缝网压裂裂缝间距的优化[J].石油钻探技术,2014,42(1):86-90.
Shao Shangqi,Tian Shouceng,Li Gensheng,et al.Fracture spacing optimization for fracture-network fracturing in horizontal wells[J]. Petroleum Drilling Techniques,2014,42(1):86-90.
[18]李小刚,罗丹,李宇,等.同步压裂缝网形成机理研究进展[J].新疆石油地质,2013,34(2):228-231.
Li Xiaogang,Luo Dan,Li Yu,et al.Advances of mechanism study of fracture networks formed by simultaneous fracturing process[J]. Xinjiang Petroleum Geology,2013,34(2):228-231.
[19]Green A E,Sneddon I N.The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid[J].Mathematical Proceedings of the Cambridge Philosophical Society,1950,46(1):159-163.
[20]Bunger A P,Zhang X,Jeffrey R G.Parameters affecting the interaction among closely spaced hydraulic fractures[R].SPE 140426,2011:292-306.
[21]刘立峰,张士诚.通过改变近井地应力场实现页岩储集层缝网压裂[J].石油钻采工艺,2011,33(4):71-74.
Liu Lifeng,Zhang Shicheng.Net fracturing by changing the surrounding in-situ stress in shale reservoirs[J].Oil Drilling&Production Technology,2011,33(4):71-74.
[22]纪宏博,李贵长,光新军,等.页岩气储层改造有效性分析[J].石油天然气学报(江汉石油学院学报),2011,33(9):145-149.
Ji Hongbo,Li Guichang,Guang Xinjun,et al.Analysis of fracture efficiency in shale gas reservoirs reconstruction[J].Journal of Oil and Gas Technology(Journal of Jianghan Petroleum Institute),2011,33(9):145-149.
[23]Fisher M K,Heinze J R,Harris C D,et al.Optimizing horizontal completion techniques in the Barnett shale using microseismic fracture mapping[R].SPE 90051,2004:1-11.
[24]Kresse O,Weng X,Gu H,et al.Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations[J]. Rock Mechanics and Rock Engineering,2013,46:555-568.
(本文编辑:李在光)
Fracture spacing optimization for horizontal well alternating fracturing and influencing factors
YANG Zhaozhong1,SU Zhou1,2,LI Xiaogang1,ZHANG Cheng3,XIE Zhongcheng4,DENG Ke5
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China;2.Research Institute of Oil and Gas Engineering,PetroChina Tarim Oilfield Company,Korla 841000,Xinjiang,China;3.Tarim Engineering Company,Chuanqing Drilling Engineering Company Limited,CNPC,Korla 841000,Xinjiang,China;4.Engineering Technical Operation Center of CNOOC Shanghai Branch,Shanghai 200030,China;5.Northeast Sichuan Gas Field,PetroChina Southwest Oil and Gas Field Company,Dazhou 635000,Sichuan,China)
For creation of large-scale effective complex fracture networks of unconventional oil/gas plays,fracture spacing for alternating fracturing should be optimized.Started from the effect of total induced stresses on initial horizontal stress anisotropy,the total induced stresses computational model of two adjacent hydraulic fractures with different fracture height and fracture net pressure was built.Subsequently,optimization approaches for critical fracture spacing of the first two hydraulic fractures and optimal fracture initiation position of the third one were proposed.Theanalysis result shows that critical fracture spacing between the first two hydraulic fractures decreased with the increase of Poisson's ratio,and increased with the increase of fracture height and fracture net pressure;the optimal fracture initiation position of the third fracture apart from the first one decreased with the increase of Poisson's ratio,and increased with the increase of fracture height.However,fracture net pressure has negligible impact on the optimal fracture initiation position of the third fracture.Finally,with comparison and analysis of a case study,the optimization results of the proposed approaches were proved to be much more advantageous and economic over the existed one,which is of significant guidance for creation of complex fracture networks with alternating fracturing technology in unconventionaloil/gasreservoirs.
alternatingfracturing;complexvolumetric fracture networks;stress shadow;principle ofsuperposition;fracture spacingoptimization
TE357.1
A
1673-8926(2015)03-0011-07
2014-10-08;
2014-11-03
国家自然科学基金石化联合基金重点项目“页岩气低成本高效钻完井技术基础研究”(编号:U1262209)和国家重大科技专项“深煤层煤层气增产改造技术研究”(编号:2011ZX05042-002-001)联合资助
杨兆中(1969-),男,博士,教授,主要从事低渗透油气藏增产改造与油气藏数值模拟研究的教学和科研工作。地址:(610500)四川省成都市新都区新都大道8号西南石油大学油气藏地质及开发工程国家重点实验室。电话:(028)83032338。E-mail:yzzycl@vip.sina.com。
