一种带翻转预处理的相位非线性误差计算方法

华琴娣，田丽鸿

（1.南京国睿安泰信科技股份有限公司，南京　210036；2.南京工程学院通信工程学院，南京　211167）

一种带翻转预处理的相位非线性误差计算方法

华琴娣1，田丽鸿2

（1.南京国睿安泰信科技股份有限公司，南京210036；2.南京工程学院通信工程学院，南京211167）

0　引言

相位非线性误差（也称相位线性度）是微波模块的重要指标之一。在微波模块测试技术中，相位非线性误差指的是微波模块在某一频段内相位的非线性误差，反映了微波模块对输入信号造成的相位失真［1］。该指标在实际考核过程中采用非线性度误差算法的概念，对相位值使用曲线拟合方法，根据目标拟合曲线与相位值之间的偏差进行计算。

曲线拟合方法是诸多实验和工程实际中广泛应用的数据处理方法，在测量工作中，通常根据测定的一系列坐标点，选取一定的数学模型拟合直线、二次曲线或者其他高次曲线，拟合的目的是根据测量点寻求曲线特征，求解曲线的相关参数，为分析实验结果提供必要的基础信息［2］。而在微波模块测试过程中，其相位数据在测量仪器上表现为折线形式，因此在使用曲线拟合方法之前，必须首先确定相位的目标拟合曲线，然后再使用数学模型进行曲线拟合，从而获取微波模块的相位非线性误差。

1　拟合曲线的确定

1.1问题描述

微波模块的相位测试值表示为公式（1）：

式中n为测试点数，fn为测试频率，pn为测试频率fn对应的相位值，（pn，fn）为一组数据对。

相位值实质上是当前被测模块与校准状态相位间的差值，在微波测试技术中，被测模块的相位值随着频率的递增而单调增加，但是在测试仪器上显示出来的相位值，取值区间为-180°～+180°。根据曲线拟合的概念建立直角坐标系，横轴为测试频率值，纵轴为相位值，把仪器测量得到的相位数据对（pn，fn）逐一画在该坐标系中，得到的曲线为相位仪器显示值的相位曲线，该曲线为一条折线，因此将产生折点。曲线拟合通常采用最小二乘法，众所周知，使用最小二乘法产生的目标曲线为直线，而相位仪器显示值在同一坐标系中为折线，目标曲线和相位仪器显示值曲线形式不同，使用拟合方法计算出来的结果不具备参考价值。为了使被测微波模块的相位仪器显示值更接近微波模块相位的实际情况，必须消除相位仪器显示值曲线上的折点，使相位仪器显示值的曲线表现为类似直线形式。

1.2翻转预处理

综上所述，相位仪器显示值是按象限概念给出的，取值区间为-180°～+180°，其值可能具有周期性，而通常我们所说的角度也是按象限取值的，只是取值区间为0°～+360°，因此只需把相位仪器显示值转换为取值区间为0°～+360°的相位实测值，其数值（可能也具有周期性）显示该相位所在象限。例如，某个相位实测值为θ （0°≤θ≤360°），另一个相位实测值为θ+n·2π（n≥0），则在仪器测试中这两个相位实测值给出的值是同一个值θ，即θ和θ+n·2π在相位实测值曲线中表现为同一个点。但是我们在使用相位实测值时，必须把这两者区分开来，使用它们的相位实际值，从而在该坐标系中得到相位实际值的类似直线的曲线形式。这就需要把相位实测值进行翻转预处理。

在相位实测值中，前两个相位实测值决定了该目标拟合直线的斜率，若前两个相位实测值中一个为θ （0°≤θ≤360°），另一个为θ°+n·2π（n≥0，0°≤θ≤360°），则使用相位实测值拟合直线和使用相位实际值拟合直线的目标拟合直线的斜率完全不同，从而导致目标拟合直线会不符合原始数据的特征，因此得出的相位非线性误差也不能反映该组相位数据的特征。为避免这种情况的出现，就必须确认前两个相位实测值是否为实际值，这取决于被测模块的特性。被测模块之间千差万别，不具备共性，因此不能通过被测模块的特性来判断相位实测值是否经过仪器翻转。但是，在测量仪器中，可以得到相位实测值的矢量表示，那样就可以确定相位实测值在直角坐标系中的具体位置，也能判断该相位实测值是否经过仪器的翻转，即可得到相位实际值。

对于相位实际值的获取，主要需要确定θ+n·2π （n≥0）的n值，假设第一个相位实际值没有经过翻转，在0≤θ≤360°内（n=0），接下来的相位实测值若是有折点，即需要翻转，则n+1，以此类推，遇到折点就翻转，n+1，n随着折点数的增加而逐渐递增。对微波模块在整个频段内的相位数据进行翻转预处理，得到该微波模块的相位实际值。

1.3曲线拟合

经过翻转预处理的相位实际值可进行曲线拟合。曲线拟合采用最小二乘法，其公式如下公式（2）所示：

综上所述，对相位实际值使用最小二乘法进行直线拟合，得到目标拟合直线。

1.4相差非线性误差计算

在直角坐标系中画出目标拟合直线和相位实际值曲线，最理想的情况下这两条直线应该重合，实际上是不可能做到的，这两条直线之间的距离就是误差。如果这两条直线形状完全一致，但不重合，例如一条直线相当于另一条的平移或直线的斜率不同，这时的误差就是线性的，否则误差就是非线性误差［4-6］。在微波模块的相位测试中，相位非线性误差这一指标的值取得是目标拟合直线和相位实际值曲线之间误差的峰峰值。

1.5抽取模型

现按仪器显示的相位值，用数据对表示成（xi，yi），把数据对画在直角坐标系中。按翻转预处理方法得到相位实际值，然后使用最小二乘法公式得到目标拟合直线Y=α+βX，该目标拟合曲线对应的相位数据对为（xi，Yi），然后计算目标拟合直线与相位实际值曲线在同一频点之间的偏差Δyi值，Δyi的计算公式如下：

然后取Δyi中的最大值和最小值，两者的差值即为所求的相位非线性误差。

2　仿真及分析

实际测试过程中，为了避免偶然误差并保证计算结果的稳定性，每组测试数据对的个数需要在201点以上。

采用仿真的方法进行分析，首先使用一组微波模块在仪器上测试时显示的相位值，设定测量频率范围、步进、测试频率点数，把测量仪器上显示的相位值画入直角坐标系中，图1表示仪器显示的相位值。

图2表示经过矢量计算后的相位实测值，在图2中还标出了相位实测值的折点。

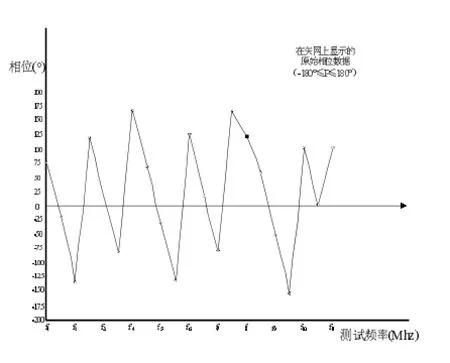
图1　仪器显示的相位值

图2　矢量计算后的相位实测值

图3描述了对相位值不处理，直接使用最小二乘法进行曲线拟合，可以看出，该目标拟合直线完全脱离了原始的相位值，无法反映这组相位数据的非线性误差。

图3　对相位值直接拟合结果　

图4描述了仪器显示的相位值经过翻转预处理后变成相位实际值，对相位实际值进行最小二乘法的直线拟合，其目标拟合直线能较好的反映相位实际值的非线性误差。

图4　经过翻转预处理的拟合结果

由表1看出，对相位数据直接使用最小二乘法拟合后计算得到的相位非线性误差大大超出实际指标范围（其值小于100°），而相位数据经过翻转预处理后进行最小二乘法拟合，计算出的相位非线性误差在实际指标范围内，说明在使用最小二乘法拟合之前对相位数据进行翻转预处理是有效的方法，且能准确地反映微波模块的相位非线性误差。

表1不同数据处理方法下拟合后的结果

3　结语

在全面分析微波模块的相位数据特征的基础上，首先排除测量误差，然后使用矢量信息计算出相位值，并提出一种对相位实测值在折点上需翻转预处理的理论，把经过预处理的相位数据使用最小二乘法进行直线拟合，计算出所有测试点的偏差值，并计算出所有偏差值中的最大值和最小值，两者之差即为相位非线性误差。使用该算法得到的目标拟合直线贴近原始数据，最大程度地反映了相位实际值的特性，得到的相位非线性误差值更为精确。

目前该方法运用于多种微波模块的测试，经实际验证能比较精确地反映相位非线性误差指标。在今后的实践过程中，通过总结各类微波模块的相位值特性，对各类模块相位值的翻转预处理做更深入的研究，将对相位非线性误差的测量将有更大的实际意义。

［1］郑君里，应启珩，杨为理.信号与系统［M］.高等教育出版社，2007，12:316-329.

［2］王桂增，叶昊.主元分析与偏最小二乘法［M］.清华大学出版社，2012，8:81-87.

［3］周继芗.实用回归分析方法［M］.上海大学科技出版社，1990:138-143.

［4］李立功，年夫顺，王厚军，刘祖深，田书林.现代电子测试技术［M］.北京：国防工业出版社，2008.

［5］王晓东，袁桂祁，于周秋.相控阵炮位侦校雷达自适应调度设计［J］.南京：现代雷达，2010，（11）：38-41.

［6］聂冰，陈庆孔.微波功率管特征参数测试［J］.南京：现代雷达，2011（5）：74-76.

Phase Linear Error；Nonlinearity Error；Turning Point；Data Turnover；Least Square Method

An Achievement for Computing Method of Phase Nonlinearity Error

HUA Qin-di1，TIAN Li-hong2
（1.Nanjing Glarun-Atten Technology Incorporated Company，Nanjing 210036；
2.School of Communication Engineering，Nanjing Institute of Technology，Nanjing 211167）

1007-1423（2015）29-0014-04

10.3969/j.issn.1007-1423.2015.29.004

华琴娣（1977-），女，江苏省南京人，工程师，硕士，研究方向为电子设备测试系统

2015-09-08

2015-09-30

相位非线性误差是微波模块的一项重要指标，通过全面分析相位数据的特征，提出一种对相位数据进行拟合前翻转预处理，再利用最小二乘法进行直线拟合，从而计算出微波模块相位非线性误差的新型测量方法，该方法通过软件仿真实现，将这种计算方法运用于多种微波模块测试，实际测试结果在测试指标范围内。

相位非线性误差；非线性误差；折点；数据翻转；最小二乘法

田丽鸿（1972-），女，宁夏中宁人，副教授，硕士，研究方向为电子信息科学与技术

Phase non-linear error is an important indicator of microwave module，through a comprehensive analysis of the characteristics of the phase data，proposes a flip pretreatment before the phase data fitting，uses the least square method for linear fitting，so as to calculate the microwave module phase new measuring method of non-linear error，the method is implemented through software simulation，the calculation method used in a variety of microwave modules，the actual test results in the range of test index.