改进的光伏组件工程数学模型建模方法
2015-09-21李善寿
李善寿,张 兴
(1.合肥工业大学 电气工程与自动化学院,安徽 合肥 230009;2.安徽建筑大学 智能建筑重点实验室,安徽 合肥 230601)
0 引言
光伏电池及组件的数学模型是研究光伏发电系统工作特性的重要基础之一,模型的准确性是确保光伏系统分析与设计正确、可靠的前提[1],因此研究光伏组件输出特性的建模问题对光伏发电技术具有重要的理论与实践意义。
光伏电池及组件输出特性的建模问题,一直都是光伏发电技术研究的热点。在已有的各种数学模型中,基于物理等效电路的隐含指数方程模型[2-4]精度比较高,能很好地体现出光伏电池内部的P-N结特性,但隐含方程不易求解,模型参数难以测量,不便于工程应用;基于试验数据拟合的多项式及分段多项式模型[5-6]需要大量的试验样本数据,同时环境变化时模型的泛化能力较差;从工程应用出发建立的基于光伏组件出厂参数的工程数学模型[7-10]较好地克服了前2种模型的不足,但现有工程数学模型的建模精度不高,与实测数据间存在超过6%的模型误差[8]。
为了提高光伏组件工程数学模型的建模精度,本文首先指出了现有工程模型误差较大的原因,然后通过推导不同工况下光伏组件输出特性的变化规律,分析现有工程模型建模参数选取方法存在的不足,提出相应的改进措施,并建立改进的工程数学模型。最后,通过对比仿真与试验验证所提方法的有效性、精确性。
1 光伏电池模型
1.1 光伏电池的物理模型
光伏电池的单二极管等效电路模型[1-4]如图1所示,其正向工作的U-I特性方程如式(1)所示。
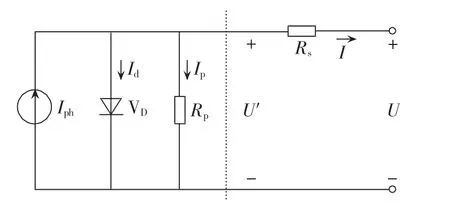
图1 光伏电池单二极管模型Fig.1 Single diode model of photovoltaic cell
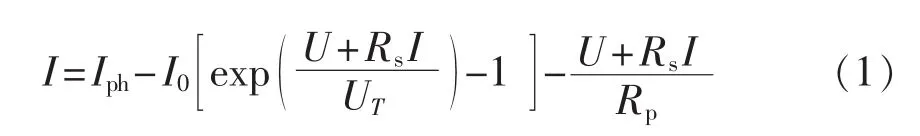
其中,U、I分别为光伏电池的输出电压和电流;Iph为光生电流;I0为P-N结等效二极管的反向饱和电流;UT=AkT/q 为温度电势,q 为电子电荷(1.602×10-19C),A为P-N结等效二极管(非)理想因子,一般取值1~1.25,T 为电池温度;k为 Boltzman常数(1.38×10-23J/K);Rs、Rp分别为等效串联电阻和等效并联电阻。
式(1)所示模型较好地体现了光伏电池内部各种因素对光伏电池输出特性的影响,已被广泛应用于光伏系统的理论分析之中,但其中的参数Iph、I0、Rs、Rp、A 等都不易测量,同时隐含方程不易求解[4,10-14]。
1.2 光伏电池的工程数学模型
针对隐含指数模型求解困难、模型参数难以测量的问题,文献[6-9]研究了基于光伏组件出厂技术参数(短路电流Isc0,开路电压Uoc0,最大功率点电流Im0、电压Um0,开路电压温度系数koc,短路电流温度系数ksc,最大功率温度系数kpm)的建模方法,构建了光伏组件的工程数学模型,如式(2)、(3)所示。
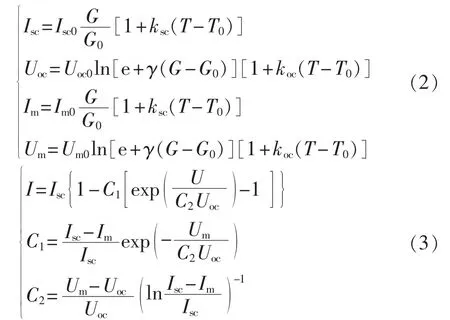
其中,G0=1000W/m2、T0≈298.16K 分别为标准测试条件下的辐照度和电池温度;G、T分别为实际辐照度和电池温度;Uoc、Um、Isc、Im为不同工况下的建模参数;γ为开路电压对辐照度的敏感系数。电池温度T与环境温度Ta、辐照度G之间的关系为T=Ta+kGG,其中光致温升系数[8,15-16]kG≈0.032 °C/(m2·W-1)。 式(2)为任意工况下建模参数的获取公式。
式(2)、(3)所示的解析指数方程克服了隐含指数方程的求解困难问题,但存在如下2点主要不足:
a.任意工况下建模参数获取公式中,光伏电池输出特性与辐照度间关系同光伏电池实际特性不符;
b.建模过程中忽略了Rs、Rp的影响,由于Rs对最大功率点电压具有较大影响[10-12],导致现有工程数学模型与实测曲线之间的拟合误差较大。
2 工程数学模型的改进方法
2.1 任意工况下建模参数的获取
针对现有模型建模参数计算存在的不足,下面将通过推导辐照度G与开路电压Uoc和最大功率点电压Um的关系提出改进方法。在温度不变的条件下,式(2)中辐照度G与开路电压Uoc和最大功率点电压Um的关系为:
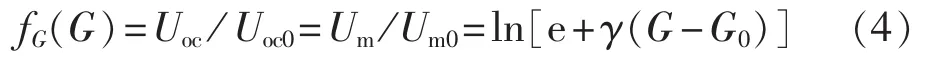
由光伏电池单二极管模型可得任意工况下开路电压的表达式为(注:Iph≈Isc):
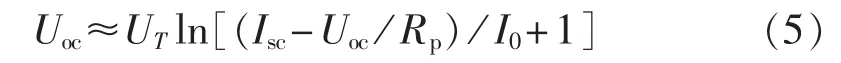
在温度不变的条件下,忽略Rp的影响时,近似有:
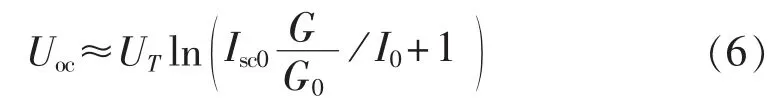
将G=G0代入式(6)可得Uoc0的表达式,进而可以得到辐照度G与开路电压Uoc的关系式:
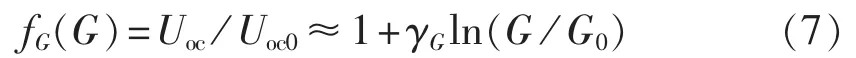
其中,γG=UT/Uoc0取值范围为 0.0405~0.05,γG的取值与理想因子A有关,一般取γG=0.041。
对于辐照度G与最大功率点电压Um的关系,同样可基于理想二极管模型下最大功率点的定义获得,在温度不变时,任意辐照度下,最大功率点电压与辐照度的关系为:
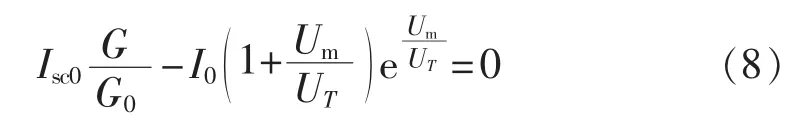
又由G=G0时开路电压Uoc0的关系可得:
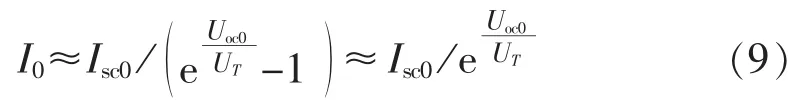
将式(9)代入式(8)进行化简,两边取对数可得:
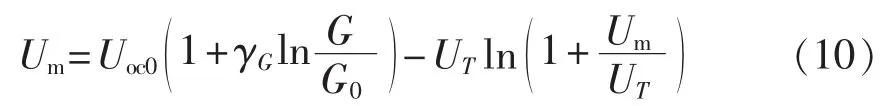
将G=G0代入式(10)可得Uoc0与Um0的关系:
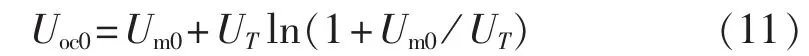
将式(11)代入式(10)并展开,同时考虑到理想光伏电池近似存在,有:
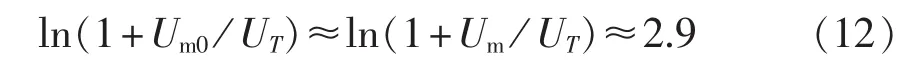
故辐照度G与最大功率点电压Um关系近似有:
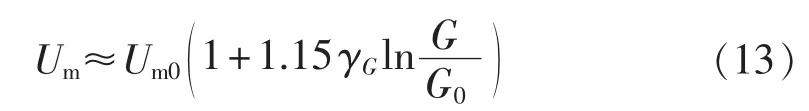
式(7)、(13)是基于理想二极管模型获得的辐照度G与开路电压Uoc和最大功率点电压Um的关系。
2.2 原始建模参数的选择
式(2)中除辐照度与开路电压、最大功率点电压关系式误差较大之外,选择Um0作为建模参数也是导致曲线拟合误差较大的原因。现有工程数学模型是在忽略了Rp、Rs的影响下获得理想光伏电池的函数关系,所以建模参数应该选择理想情况下的最大功率点电压Um0′,这样才能使工程模型在最大功率点处的导数为零。理想光伏电池的最大功率点电压与开路电压之间存在近似的比例关系[3],即:

其中,kA取值范围为0.865~0.875。
此外,式(2)中最大功率点电压、开路电压采用同样温度系数也是导致模型误差较大的原因,选择最大功率点功率的温度系数kpm作为最大功率点电压的温度系数可以显著减小误差。
令 ΔT=T-T0,式(7)、(13)、(14)代入式(2),可得改进的建模参数获取公式:
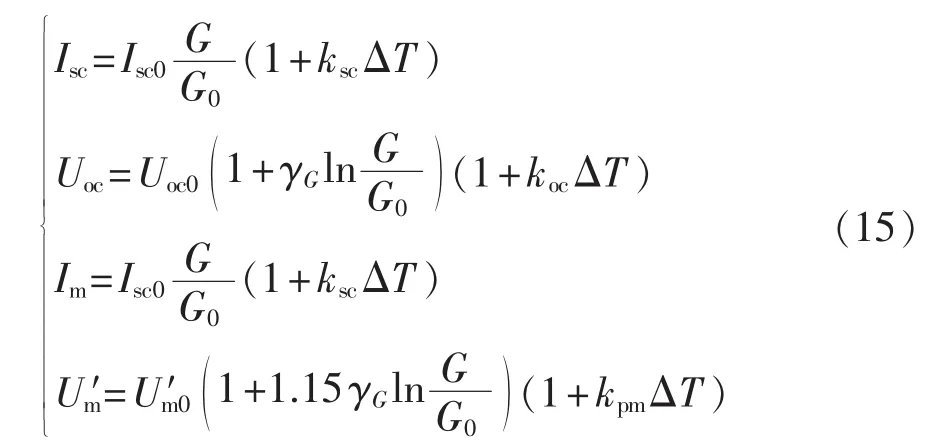
2.3 改进的解析指数工程模型
如文献[8]所述,令解析指数模型的方程为:
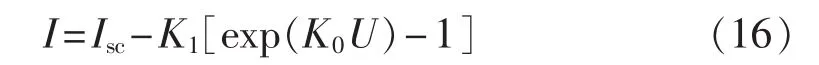
式(16)通过(Isc,0)、(Im,Um′)、(0,Uoc)3 个点是工程数学模型需要满足的必要条件。式(16)显然通过(Isc,0)点,由式(16)通过(Im,Um′)、(0,Uoc)可得:
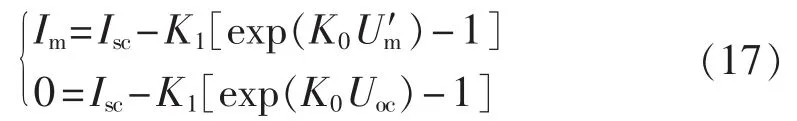
联合式(17)中的两式,同时有 exp(K0Uoc)≫1、exp(K0Um′)≫1,故可得:
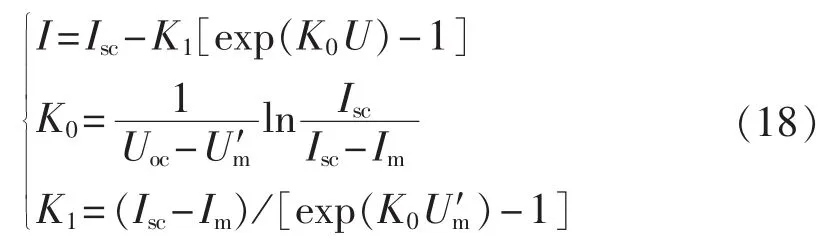
式(18)是理想光伏电池的工程数学模型,所以必须将其最大功率点从(Im,U′m)修正到(Im,Um)点。 式(16)改写为电压输出模型,由于实际输出电压U与理想输出U′的差值,就是串联电阻Rs上的压降,故有修正的电压输出模型为:
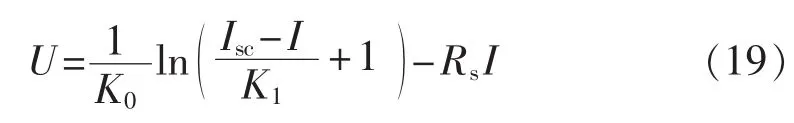
串联电阻Rs可以用下式估算:

改进后的电压输出解析工程数学模型为:

3 仿真与实验分析
3.1 改进工程模型与物理模型仿真对比分析
为了验证式(15)、(21)所示的改进工程数学模型的有效性,选择英利集团的YL310P组件为仿真对象,首先,通过对比工程数学模型仿真输出曲线与物理模型仿真输出曲线的重合程度来体现该方法的有效性。组件参数及仿真参数如下:Uoc0=45.6V,Isc0=8.99A,Um0=36.3V,Im0=8.53A,ksc=0.045%,koc=-0.34%,kpm=-0.44%,γ=0.0003,γG=0.041,kA=0.875。
标准条件(G=1000 W/m2,Ta=298.16K,不考虑电池温升)下的仿真对比曲线如图2所示。
定义工程模型与物理模型的最大功率误差除以物理模型的最大功率为拟合误差。则由图2中功率误差曲线可见,现有工程数学模型的拟合误差约为22%,改进工程模型的拟合误差为1.3%。
考虑温升系数 kG≈0.032 °C/(m2·W-1)时,不同辐照度下的仿真曲线对比如图3所示。
由图3可见,在考虑光致温升系数时,不同辐照度下改进的工程数学模型与物理模型同样具有非常高的拟合精度。由图2、3可知,改进的工程模型与物理模型之间具有较高的拟合精度。
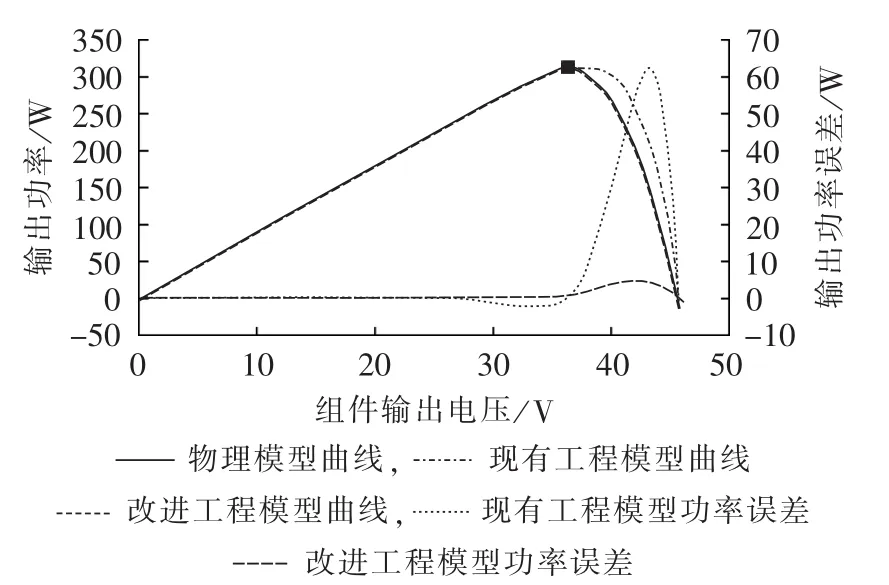
图2 工程模型与物理模型的对比曲线Fig.2 Comparison of curves between engineering model and physical model
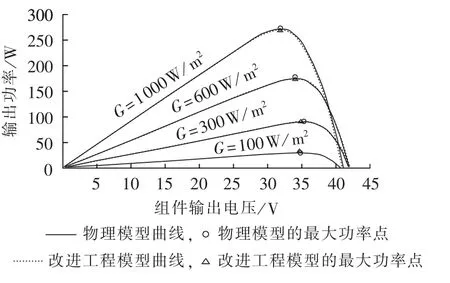
图3 不同辐照度下工程模型与物理模型的拟合曲线Fig.3 Fitting curves of engineering model and physical model for different irradiances
3.2 改进工程模型与试验数据的误差分析
a.工作环境 (Ta=293.16K,G=800W/m2,kG≈0.032 °C/(m2·W-1))下 10 个型号光伏组件出厂实测参数的误差分析。仿真模型输出数据用Pm_s、Um_s、Im_s、Uoc_s、Isc_s表示,组件实测 NOCT 电气参数用 Pm、Um、Im、Uoc、Isc表示。 定义开路电压相对误差 Eoc,最大功率点电压、电流、功率相对误差 EUm、EIm、EPm,短路电流相对误差Esc分别为:
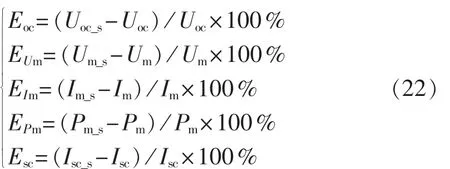
数据来源于天合和英利光伏组件数据手册中提供的正常工作条件下的组件参数(NOCT电气参数),图4为不同型号组件关键参数的建模误差,图中横轴1—10分别代表组件型号DC05A-260、DC05A-270、PC14-295、PC14-310、DC80-215、YL260C、YL280C、YL290P、YL310P、YL260P。
由图4(a)可见,现有工程模型最大功率点电压误差超过2%的有9个型号,最大功率点电流误差超过2%的有5个型号,开路电压误差超过1%的有6个型号,各种误差的最大值超过了6%。对比图4(b)可见,改进工程数学模型对所有型号的光伏组件误差均小于2%,其中英利光伏组件的模型误差均小于1%。可见改进后的工程模型对不同型号的组件均具有比较高的建模精度。
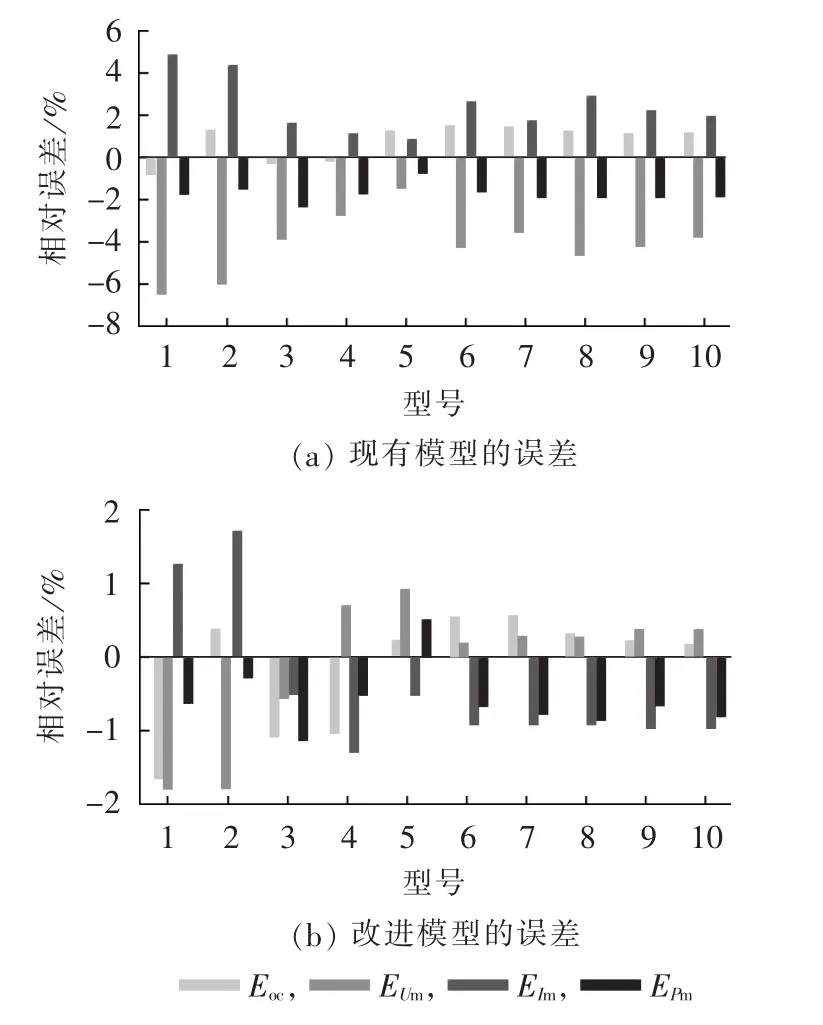
图4 不同型号组件关键参数的建模误差Fig.4 Modelling error of key parameters for different module types
b.不同辐照度下(温升系数为零)光伏组件输出特性参数误差分析。样本组件的标称参数为Im0=8.11 A,Um0=28.73 V,Uoc0=36.9 V,Isc0=8.75 A。
数据来源于振兴光伏新能源有限公司提供的光伏组件在不同辐照度下的实测数据(光伏组件测试仪XJCM-9A)。图5为不同辐照度下关键参数的建模误差。
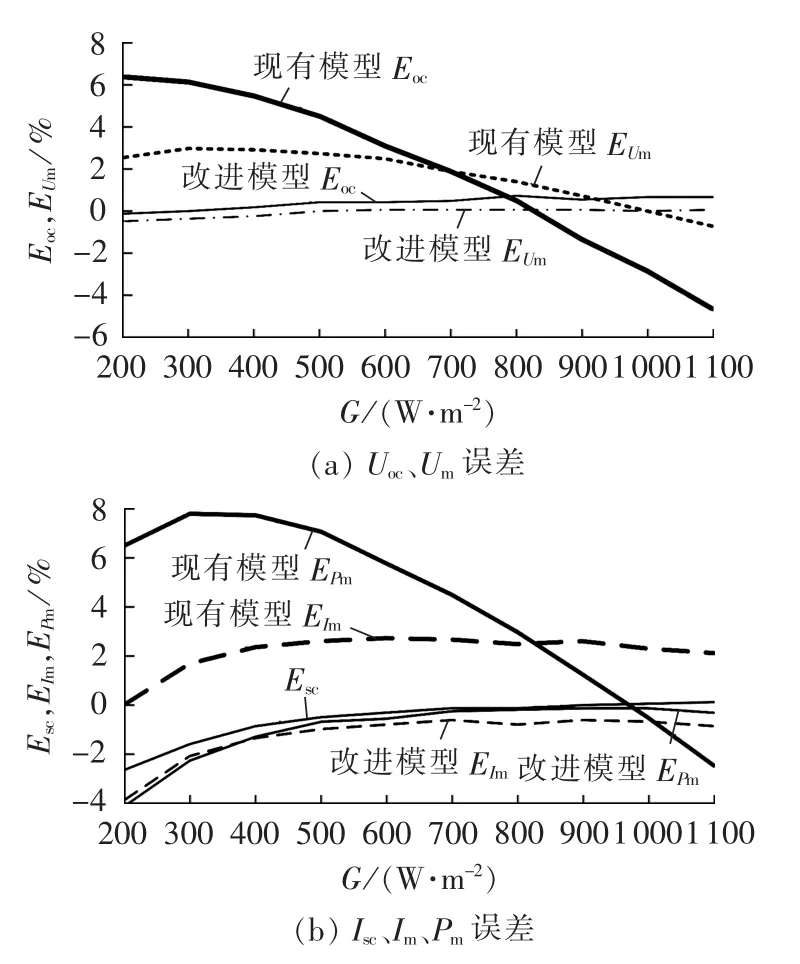
图5 不同辐照度下关键参数的建模误差Fig.5 Modelling error of key parameters for different irradiances
由图5(a)可见,不同辐照度下改进后的工程模型的开路电压、最大功率点电压的误差均小于0.5%,而现有模型的最大开路电压误差却达到了6%。由图5(b)可见,在辐照度大于400W/m2的区间,改进工程模型的误差均小于1%,在辐照度小于400W/m2的区间,由于短路电流误差Esc的增加,导致改进模型的误差有所增加。而现有模型存在接近8%的最大功率误差。由此可见,改进后的工程模型在较大辐照度范围内都具有比较高的建模精度。
c.不同辐照度下(温升系数为零)光伏组件输出特性曲线拟合误差分析。
为了进一步验证改进模型与实测数据曲线的拟合精度,图6给出了3种不同辐照度下实测数据曲线与仿真曲线的误差。为了定量描述拟合误差的大小,定义不同辐照度下最大输出功率误差除以实测最大功率为拟合误差。则由图6可见,辐照度为1000W/m2时,其拟合误差为-3.02%;辐照度为500 W/m2时,其拟合误差为1.86%;辐照度为200W/m2时,其拟合误差为9.7%。
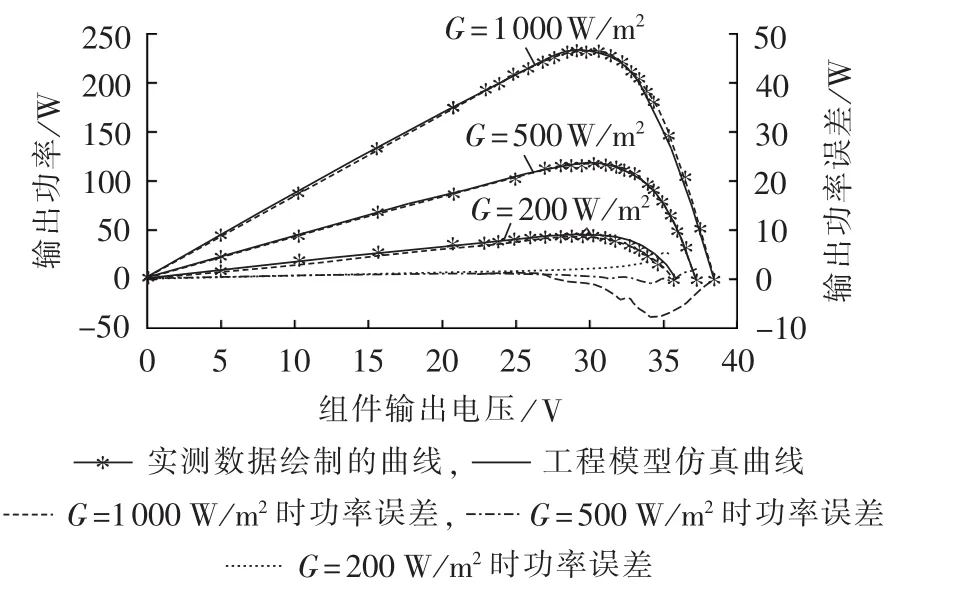
图6 不同辐照度下组件实测特性曲线与仿真曲线对比Fig.6 Comparison between measured and simulative module characteristic curves for different irradiances
4 结论
通过分析光伏电池输出曲线的特征,针对现有光伏组件工程数学模型建模过程存在的不足,给出了工程建模的改进方法,建立了一种改进的工程数学模型。具体优点可归纳为:
a.该工程数学模型与物理模型之间具有较高的拟合精度,曲线拟合误差小于1.5%;
b.该工程数学模型对不同型号光伏组件关键参数的建模精度最大误差不超过2%;
c.该工程数学模型在较大辐照度范围,与实测数据曲线的拟合误差不大于10%,关键参数建模误差不超过4%。
