基于数据融合与拓扑分析的多阶段月度网损计算

王 峥，刘创华，刘怡然，于光耀，卢志刚

（1.国网天津市电力公司电力科学研究院，天津 300384；2.国网天津市电力公司运维检修部，天津 300010；3.燕山大学 电力电子节能与传动控制河北省重点实验室，河北 秦皇岛 066004；4.国网冀北电力有限公司青龙县供电分公司，河北 秦皇岛 066500）

0 引言

网损计算是电力企业的基本工作，亦是考核企业经营与管理水平的重要手段[1]。目前在各大电力企业中，网损计算主要有统计线损计算和理论线损计算两方面。统计线损主要由关口计量表所得的数据来计算，理论线损通常是指在某一个代表日下断面网损的和值。统计线损包含理论线损和管理线损，理论线损与网架结构和参数有关，管理线损主要表征输电线路的管理水平[2]。

目前理论计算多采取典型日24点法，或基于神经网络[3]、SCADA 采集的网损计算方法[4]等。 但由于断面数据量非常庞大，因此每次理论线损计算需耗费大量的人力物力，且持续的理论线损计算也是系统不能承受的。同时，由于月间的负荷是变化的，并受多种因素影响，且月间会发生电网运行方式变化、电网检修及电网结构变化等多种状况，因此仅用代表日理论线损表征一个月甚至一年的理论线损状况与实际不相符，十分不合理。但是由于系统的非线性，网损ΔP往往不能表示成时间的解析函数，因此不能积分求出网损的解析表达式，只能用数值法求解[5]。那么采集的频率与精度以及计算的次数将直接影响到计算结果的准确性。假设采集频率无限大，那么将会有效防止突变量，网损值可转化成数值方法求解。但采集频率大，又造成了数据量过大的问题，持续的理论线损计算显而易见是不可用的，因此，聚类技术[6-8]成为了处理具有相似性的大数据的新方法，它能根据数据自身的特点自动分为不同的聚类簇，簇内数据相近，簇外数据相异性大，从而简化数据的计算和分析。

在此基础上，本文选取断面特征向量，利用聚类技术对月间大量断面进行聚类，选取典型断面计算并推算月度网损。由于月间的拓扑和运行方式会发生变化，因此需将月度计算分为几个阶段进行，但在电网结构变化十分微小时，时间阶段的划分过多会影响计算速度，造成大量历史数据浪费，本文提出一种基于拓扑辨识[10-12]的月度断面时间阶段划分原则，该技术在实现电网拓扑的快速跟踪方面有一定应用。而针对采集频率高造成的参与计算断面数量多，融合思想[13]在军事等领域都有实质性的应用，本文提出基于融合思想的断面数量削减方法，减少聚类的断面数量，增加计算速度。然后，根据上述理论提出基于最近邻聚类的多阶段的月度网损的计算流程。

1 拓扑辨识与时间阶段的划分

1.1 拓扑辨识方法

按CIM术语，电网拓扑分析是将厂站内闭合的开关（刀闸）相连的连接节点（connectivity node）组成拓扑节点（topological node）集合，并根据网络中支路（包括路、变压器等）的连接关系，将有电气联系的拓扑节点归并到一个拓扑岛（topological island）。通常根据求取节点的邻接表Aj进一步进行拓扑连接分析，以判断开关的闭合与断开、厂站的增加与减少。

以电网中第k片为例，在短时间内，电网拓扑结构一般仅发生局部变化，则可对比原有拓扑与当前拓扑的邻接表Cnctk-1，判断拓扑的连通性和相异性。

则根据实际情况有以下4种结果：

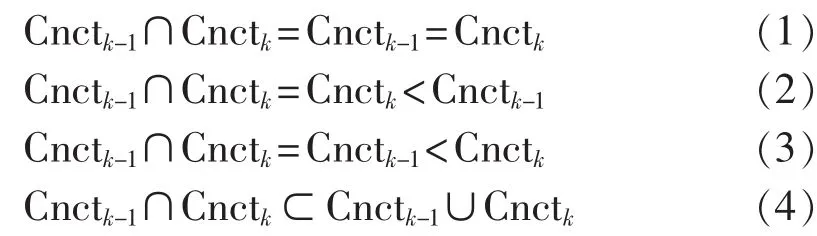
情况（1）：表示相邻两时段的连通性未发生变化，因此拓扑结构也未改变，阶段性保持一致。

情况（2）和情况（3）：分别表示在下一断面有节点退出运行或节点增加，需根据节点的重要程度及对网损的影响程度判断是否需划分为新的时间阶段。

情况（4）：表示下一断面既有节点增加又有节点退出，情况较复杂，需综合分析节点的影响再做判断。

1.2 时间阶段的划分

对于上节的情况（2）—（4），当节点的增加 /减少或者开关的闭合等不改变电网中潮流的分布时，则可认为此种状况与前一时间电网状态属于同一阶段。而根据拓扑分析结果，可定义如下情况。

（1）新增或者减少边缘节点：即在电网中新增（减少）1个或几个只与1个节点相连接并且向下带负荷的节点，并且其余节点的连通性不发生变化，如图1所示节点40、41。

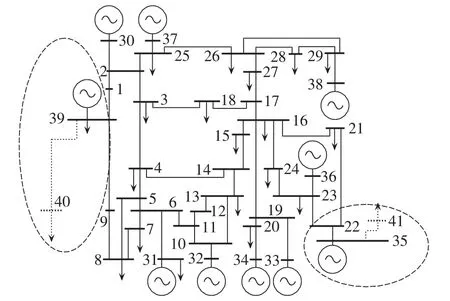
图1 电网拓扑实例图Fig.1 Example of grid topology

此时 Cnctk-1-Cnctk=m，n，…，其中 m、n 为新增（减少）的节点编号。

同时定义拓扑变化因子α，其表示新增节点所连接的设备阻抗zi与中心断面未变化电网结构的阻抗zj之和的比值：

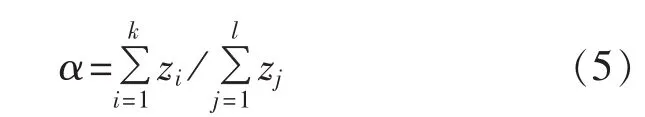
当α保持在阈值γ以内时，将此时段与上一时段划分为相同时段，同时在计算时将边缘节点与其直接相连的节点融合，将增加的边缘节点作为一个负荷来处理，如图1将节点39与40融合，将节点40作为节点39的特殊负荷，从而保持与之前电网相同的节点状态。同理，节点41也做相同处理。在进行聚类计算时，需计算与数据库中属于同一时段的所有中心的拓扑变化因子，如果α仍然在规定范围内则可与其进行聚类计算，否则只能与α满足条件的中心进行聚类；当α大于阈值γ时，那么将此阶段划分为一个新的时间阶段，将此前的中心封存在数据库中，从头开始进行新一轮的计算。

（2）新增或减少连接节点：即此节点与2个或多个节点连通。

如此则需判断在正常运行模式下的开关状态，其电网连通性是否有变化，如无变化则可当作边缘节点处理，如有变化则划分新的时间阶段。

（3）节点数目不变，但是开关的连接（连通性）发生变化。此时可分为以下几种情况。

a.线路或者设备检修，并且其有作为备用的设备和线路，此时其对整个电网的损失影响较小，因此不再重新划分时间阶段。

b.线路或设备检修没有备用或者发生意外，导致多条线路停电，则须将该情况单独罗列计算，并将其存入数据库，如果再有相同情况发生以此作为借鉴。

c.运行方式导致的节点连通性大范围变化，即片内的节点数目变化较大，重新划分时间阶段。当然，如果此种情况在前几个时段或者数据库中有相同或者相近的记录，那么可以依照历史记录进行计算。

（4）上述3种情况同时发生时，按照有需要则重新划分时间阶段的原则来划分。

经上述分析，可将月度的电网时间断面划分为q≥1个时间阶段，可将其中的每一阶段分别进行分析研究，最后将结果进行叠加来分析月度的网损变化。

2 断面削减方法

2.1 采集频率对负荷数据精确性影响

在任意时间阶段中，负荷曲线是连续曲线，在供电企业实际应用中负荷数据一般按一定时间间隔采集，即为离散的数字量。黑龙江电能量现代化系统负荷数据采集最小间隔为15 min。图2为某大酒店某日96点、48点和47点有功负荷曲线对比图。该日的最大功率为56.616 kW（简设为1），功率因数为0.92。96点负荷数据由系统每15 min采集一次，48点和47点负荷曲线每个点的数据依次是96点负荷数据中2个点数据值的平均值，即采集间隔为30min。48点负荷曲线的第一个点为96点负荷曲线前2个点的数据平均值，47点负荷曲线第一个点为96点负荷曲线第2点到第3点的平均值。

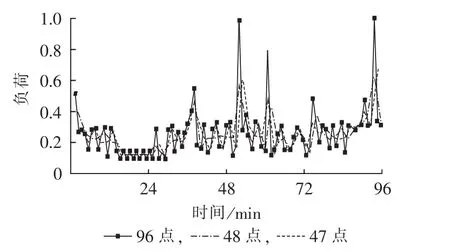
图2 96点、48点和47点负荷曲线Fig.2 96-，48-and 47-point load curves

由图2可知，96点负荷曲线和48点、47点负荷曲线最大负荷值不相同。96点负荷曲线最大负荷值为1，而48点和47点负荷曲线最大负荷值分别为 0.66和0.49。显然，96点负荷曲线比48点和47点负荷曲线更准确。即负荷数据采集时间区间大小对采集最大负荷数据值影响很大。当采集数据的时间区间一致时，采集时间间隔内负荷变动越小，采集结果越准确，即采集时间间隔内的负荷变动对计算精度造成影响也越小。月度网损是大量的断面的叠加，因此，加大采集的频率可使线损计算的精度得到提高，但同时也会增加需计算的断面数量，影响聚类速度。

2.2 基于融合理论的断面削减

为防止突变量，本文假设采集频率无限大；为防止运算量过大，运用融合思想对负荷曲线进行时间过程的划分，并提取相应时段的特征断面。划分时间过程后，在负荷缓慢平稳变化时，少量时间过程较长子时段的负荷水平可代表此时系统的真实情况；在负荷急剧快速波动时，则需较多数量的短子时段细致刻画负荷曲线攀峰降谷过程，以描述系统波动情况。

本文采用融合思想划分离散化后各子时段时间过程，其原则是保证在划分后的每个子时段中，负荷相对的波动较小，负荷曲线等值示意图如图3所示。这样划分的优点是可以保证在负荷波动平稳时，提取少许表征该时段的特征断面即可表述较接近系统的实际情况。而在系统负荷变化较大，例如负荷急剧增长或快速下降时，有更多的子时间段落中多个特征断面来描述系统负荷的变化过程。具体合并过程如下。

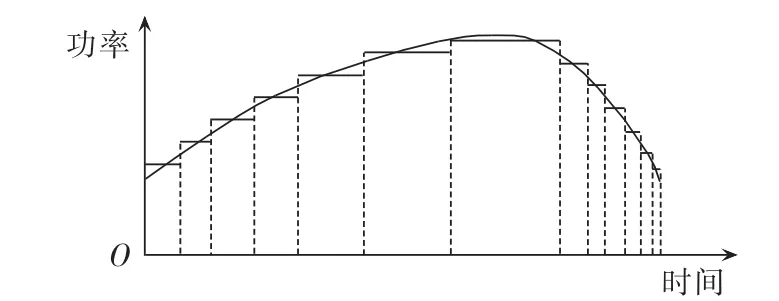
图3 负荷曲线等值示意图Fig.3 Schematic diagram of equivalent load curve

假设第m、m+1时段系统的等值有功功率分别为pm、pm+1，则第m时段与相邻的第m+1时段的负荷变化量绝对值为：

如果 Δpm≤λ（pm+pm+1），λ 为划分时允许负荷最大波动百分量，可依据实际情况选取。则将其所对应的第m时段与相邻的第m+1时段合并为一个新的第m时段，新时段的等值负荷按式（7）计算，以保证等效后研究时段内的电能量仍然相等，负荷波动较小。

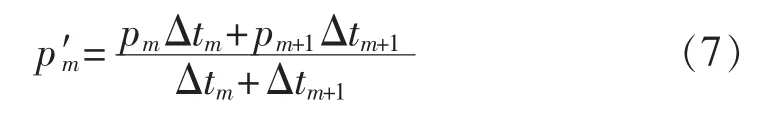
最后将计算时间范围分成n个时段Δt1、Δt2、…、Δtn，可认为该时段Δt中损耗功率变化相对较小，大多采集装置是15 min采集一次，为体现此时段的总体特征并与实际相结合，则按如下条件筛选断面。

（1）若Δt的时间段内含3组及以上的采集数据，则在20%、60%、80%左右的时间段内分别选取一个代表性的时间断面做聚类研究，每个时间段分别代表整个阶段内整体时间的1/3，在此前提下尽量选用采集完整断面，避免数据采集不完整带来的计算误差。

（2）如果Δt的时间段内包含3组及以下的采集数据，那么将其中全部的时间断面作为聚类研究的对象。与此同时，网损电量的计量方法也发生了变化。网损电量A与网损功率ΔP的关系为：

由于ΔP应是离散的且往往不能表示成时间的解析函数，因此不能积分求出网损的解析表达式，只能用数值法求解。

采用融合理论之后，假设一段时间内共有T个时间段，共有m个断面，每个断面所代表时间段持续时长为 Δti（i=1，2，…，m），网损电量可表示为：

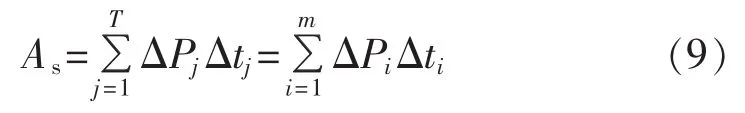
其中，As为阶段网损电量；ΔPj为第j个时间段的等值网损功率；ΔPi为第i个断面的网损功率；Δtj为第j个时间段的持续时长；Δti为第i个断面所代表的时间段持续时长。

3 基于聚类的月度网损分阶段计算

3.1 最近邻聚类

最近邻聚类法是一种较新的应用广泛的聚类算法[14-15]，其利用样本的特征向量将多个样本自动分为不同的聚类簇，把样本归于与其最近邻的聚类中心，是现有的聚类算法中的一种非常有效的聚类算法。

聚类中心的处理方式如下。

假设样本集S中有R个样本，其被分成M个聚类，第n类中共有J个样本，则第n个聚类的重心为：

其中，x（jn）为第 n类中第 j个样本。

在本文中，选取与聚类中心相似度最大的样本为类的赋值样本（中心样本）。避免因初始中心样本在类中相对于其余样本过大或过小，从而不能代表此种聚类簇平均水平的问题。

3.2 月度网损计算具体步骤

将每一个断面作为一个样本即聚类对象Xi，当有m个断面参与分析计算时，聚类的整个样本集为X=｛X1，X2，…，Xm｝，m 为聚类对象的个数。

（1）根据Cnctk与电网运行情况判断将样本划分成从属于q≥1个不同时间阶段的子集。

（2）将每个子集中的断面数据进行融合，提取出特征断面。

（3）在每个子集中，将各电源节点的注入功率与网络参数作为断面特征向量，对于数据采集缺失的断面，利用粗糙集理论[16]求取核特征向量。基本概念详见参考文献，本文中不再赘述。利用此断面之前的数据采集完整断面的聚类中心结果作为决策属性D并构造信息系统Sy，逐一去除断面的特征向量C中的第 i（i=1，2，…，q）个属性，并将其作为条件属性 P，利用P重新聚类，并计算约减后条件属性对于决策属性的依赖度r（P，D），从而找到一个相对最小的约减节点注入核特征向量集，使 r（P，D）=r（C，D）；如果之前无数据采集完整断面的聚类中心结果，则默认核特征向量集P=C。重复利用改进的最近邻聚类利用加权的欧氏距离进行相似度的计算，最终得出聚类结果和阶段网损值。

假定实时新增样本数据 Xk（k=2，3，…）时，已经存在ta个时间阶段，同时每个阶段内有Mta个聚类中心，分别为。根据Cnct与电网运行k情况判断其是否属于数据库中某一时间阶段。若是，假设其属于时间阶段ta，利用改进的最近邻聚类对其进行分类，将其分配给与样本Xk相近的中心，并根据类中的样本情况调整聚类中心；或者在不满足阈值时单独作为中心。若否，样本Xk设为时间阶段的ta+1的第一个聚类中心X（1ta+1）-c。

（4）分别得q个阶段聚类结果，各阶段的类数分别为 Mq，每个类内的样本个数为 ki（i=1，2，…，Mq），每个样本的融合时间段为timj，阶段理论线损如下：

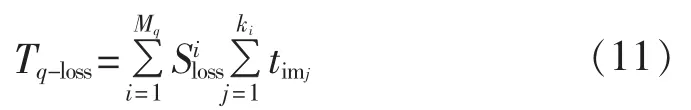
月度理论线损计算公式如下式：

4 算例仿真

本文采用我国某中等城市的实际输电网为例，利用上述方法来分析该电网中月度网损的变化情况。图4给出了该城市电网系统的站外接线图（图中方框表示电源节点，单圆圈表示220 kV厂站节点，双圆圈表示500 kV厂站节点）。

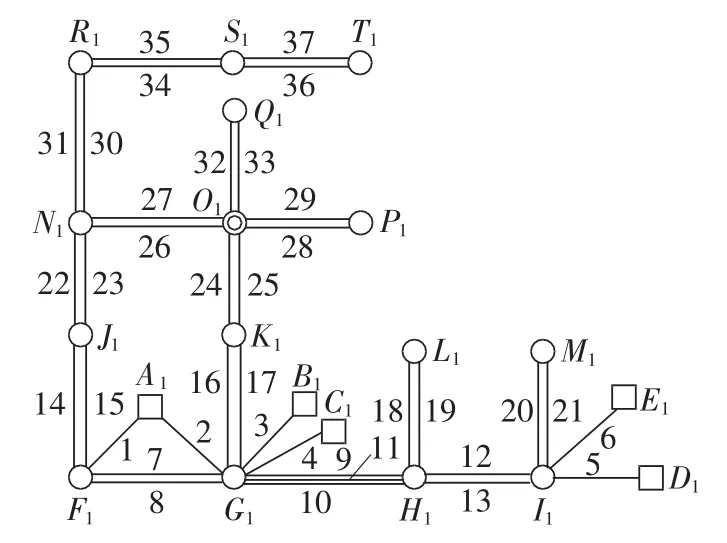
图4 系统接线图Fig.4 Wiring diagram of system

4.1 拓扑辨识与时间阶段的划分

该城市电网电压等级为220 kV，系统包括：1个本地电厂，装机容量1600 MV·A，包括6台凝气式发电机组，容量为2×200MV·A 和 4×300MV·A；1个500 kV主网的电源变电站（O1节点）；14座220 kV变电站，其中T1和Q12座变电站为联络站，即和另外一个地区电网互供电量的站；37条220 kV线路和26台高压额定电压为220 kV的三圈变压器。

电能量自动采集装置每隔15 min采集一次，每天有96个数据采集断面，根据电网实际情况，其时间阶段划分情况如表1所示。

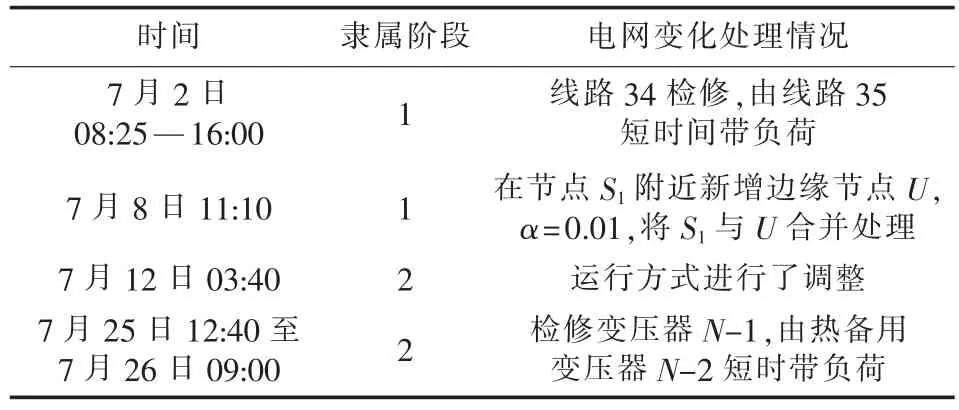
表1 月间拓扑变化情况Table 1 Monthly change of topology

可以看出，在一个月中电网共发生了4次变化。在第一个时间点中，线路34检修，场站内的母联开关2401闭合由线路35短时带负荷，此时，除线路35所带负荷过大网损升高外，对其余线路和设备潮流并无影响，因此不必另外形成新的时间阶段。在第二个时间点，电网新投运厂站U，此时新增2条线路，电抗分别为0.082 Ω/km与0.0804 Ω/km，2台变压器互为备用，电抗为分别为0.1852 Ω/km与0.1850 Ω/km，并且分担了厂站S1的部分负荷，由此可计算出α=0.0043，其值小于预设值γ=0.01，因此可假设将节点S1与边缘节点U合并为一个节点，将其注入功率和值与前阶段的节点S1注入功率对应，以计算断面相似度。在第三个时间点，由于运行方式发生变化，使电网的分隔开关发生变化，从而使电网拓扑结构和潮流分布等发生变化。因此，将此时刻前作为一个阶段进行研究，后期作为一个阶段进行研究。第四个时间节点，变压器N-1检修，由站内另一台变压器N-2短时带负荷，低压母线母联开关5201闭合，除变压器N-2所带负荷增大、网损升高外，对潮流无影响，因此不必另外形成新的时间阶段。从表1可知，利用拓扑分析的时间阶段划分方法，可有效减少月度计算中的阶段数量，使计算简便。

4.2 断面融合结果

本文算例仿真中用到的负荷数据为该城市理论线损计算软件中提供的2012年7月负荷数据，根据阶段内的负荷变化曲线，利用融合理论对采集时间段进行融合，进而减少断面数量。根据拓扑分析与采集结果，在前期阶段中，共有1067个断面数据，其中缺失数据断面为126个。后期阶段中，共有1813个，缺失数据断面为168个。

某一天的日负荷曲线如图5所示，将每15min作为一个子时段，其采集点负荷作为子时段内的平均负荷。

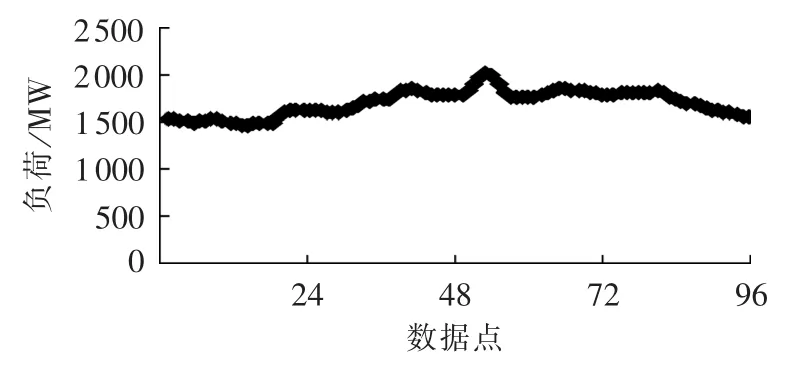
图5 日负荷波动曲线Fig.5 Daily load fluctuation

经多次试验，选取λ=0.01进行仿真。利用融合理论之后的时间段合并及采用断面结果如表2所示，表中包含断面、采用断面合计分别为96、50。由表中可以看出，参与聚类的断面数量由96个减少到了50个，在负荷攀升阶段，有一部分子阶段体现了其变化过程，而在负荷平稳的阶段，其利用少数的断面表述了其负荷特征。因此通过融合理论，前期阶段最终断面数量变为502个，数据缺失断面为40个；后期阶段最终断面数量变为631个，数据缺失断面为68个，其计算数量明显减少。

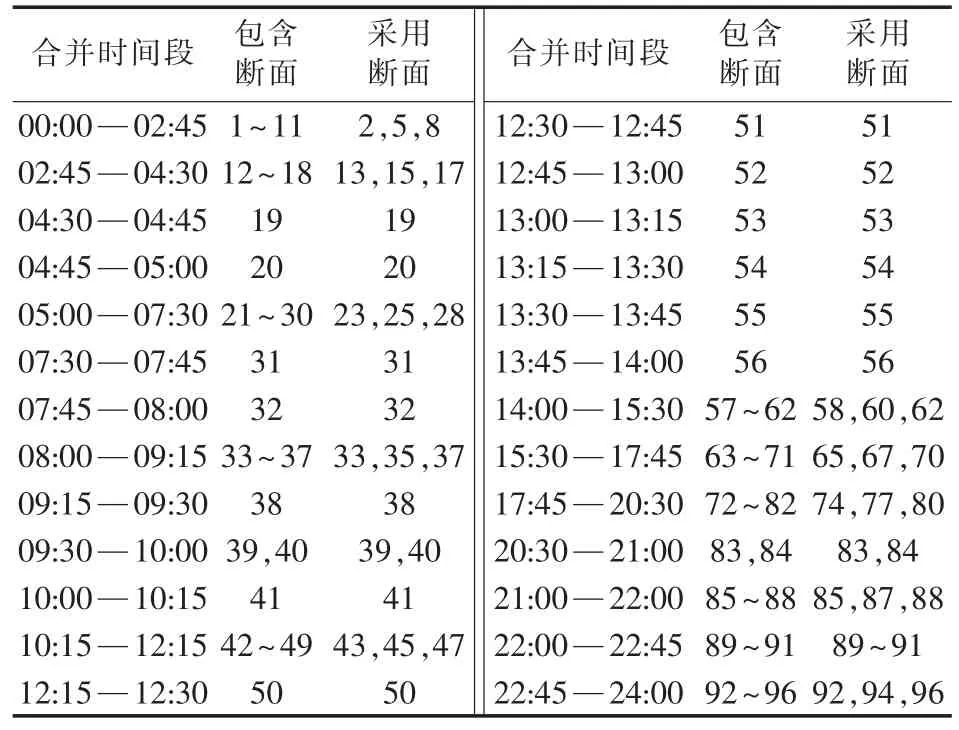
表2 96点断面融合情况表Table 2 Fusion table of 96 sections

4.3 月度线损计算

根据融合断面进行聚类计算，可得到各阶段的聚类结果。由于篇幅所限，本文只显示阶段1的完整聚类结果，如表3所示。阶段2的聚类过程与阶段1相同。不同聚类方法得到的月度网损对比结果见表4。

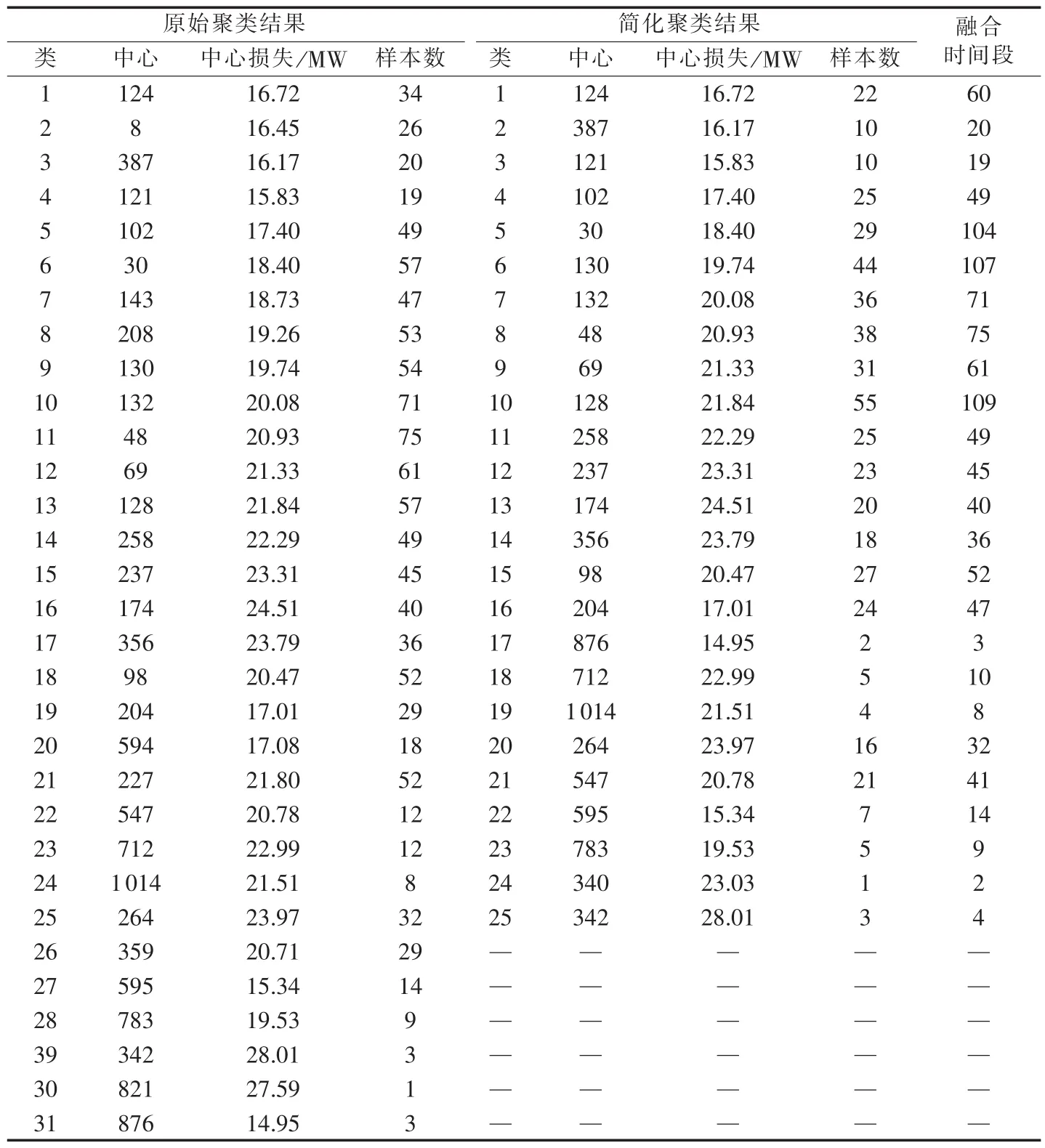
表3 阶段1聚类结果Table 3 Clustering results of section 1

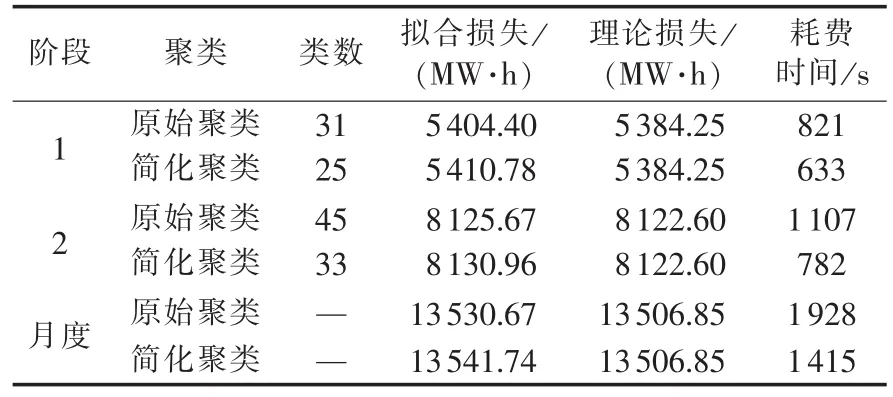
表4 月度网损对比结果Table 4 Comparison of monthly transmission losses

从表中可以看出，利用融合前后的断面数据计算得到的理论损失差别不大，阶段1误差率分别为0.38%与0.48%，阶段2误差率分别为0.038%与0.10%，月度总网损误差率分别为0.37%与0.50%。但是其参与计算数量大幅减少，计算时间由初始的1 928 s降低到了1 415 s。其在一定程度上人为避免了数据缺失断面参与计算的情况，使计算时间会相对较少，并且随着时间的增长其优势将越发明显。因此本文算法在保持一定精度的基础上能有效地减少计算量。

5 结论

本文针对断面聚类求取月度网损计算方法中存在的问题，利用拓扑辨识与融合理论，提出了一种多阶段月度网损计算方法。该方法能在月度拓扑与运行方式变化时，尽量减少时间阶段的划分频率；并且在增加采集频率的基础上，减少聚类计算量并保证一定的计算精度，从而准确刻画网损变化情况。