救援时间限制下高速公路网应急设施点选址模型
2015-09-19赵琳娜巩建国公安部道路交通安全研究中心北京100062
赵琳娜,戴 帅,巩建国(公安部道路交通安全研究中心,北京 100062)
救援时间限制下高速公路网应急设施点选址模型
赵琳娜,戴帅,巩建国
(公安部道路交通安全研究中心,北京 100062)
应急资源布局问题是高速公路应急管理的关键。通过建立数学模型,提出一种优化高速公路网中应急设施点布局方法。首先,通过分析高速公路网中应急需求的布局特点,依据事故发生概率、事故影响范围和路段平均车流量确定在某个交通事故情形下需求点的应急需求。然后,基于需求分析建立应急设施点选址模型。通过救援时间限制确定设施点的覆盖条件,选择救援时间短、物资供给能力强的待选点建立设施点。最后,采用基于拉格朗日松弛的启发式算法对模型进行求解。通过计算实例验证,该布局方法针对高速公路网的应急需求,保障了应急事件救援时间,为高速应急设施点布局提供了新思路,可适用性强。
高速公路网;应急需求;救援期限;覆盖;选址模型
0 引言
随着我国高速公路里程与日俱增,高速公路上的交通事故频繁发生,对高速应急管理系统的要求也相应提高。交通事故发生后,若不能提供及时、有效的救援措施,还可能会引发二次事故,造成更为严重的人员伤亡和经济损失[1]。目前,我国各省、各地区都实施了高速公路交通事故的紧急救援系统,但该系统的建设尚处于初级阶段,依然存在一些问题有待解决。据我国卫生部资料显示,在我国每1 000例交通事故伤者中,只有14.3%乘救护车到达医院[2],可见提高交通事故紧急救援效率迫在眉睫。如果能在高速公路网中合理地设置交通事故救援点,不仅能降低应急管理成本,还能够保证救援的及时性和有效性,避免或减少因救援不及时而造成的人员伤亡和财产损失。
应急资源选址问题可以通过建立数学模型寻找最优布局方法。Konstantinos G.Zografos[3]等提出一个关于确定危险物资运输路径和应急响应决策的支持系统:首先通过费用和风险最小选择危险品运输路径,其次根据事故响应时间确定应急资源的布局,最后依据设计安全区和消散时间决定消散路径;Paraskevi S.Georgiadou[4]提出应对大型事故的多目标应急响应优化模型,将安全情况、事故影响和经济损失作为模型的目标参数并采用改进算法对模型进行求解;Dian-liang Xiao[5]等从事故预测、应急救援方案和应急资源管理三个方面分析了高速公路应急救援系统结构,结合高速救援特点,基于救援时间建立了时间可靠度评价模型;Takeo Yama⁃da[6]在城市应急系统研究中提出了两种应急资源选址方案:一种通过寻找最短路径法确定设施点位置,另一种以设施点容量为研究目标,通过寻求最小费用法确定选址方案;Hongzhong Jia[7]等通过对传统覆盖、P-中心、P-中位模型的改进,提出了适应大规模紧急情况的救护车布局方法。
上述研究都是根据城市道路网的特点进行应急资源的优化布局,大多数模型都是以寻求费用和风险最小为目标函数,对传统选址模型进行改进,并没有考虑特定场景下存在的救援条件限制,也没有涉及高速公路网中应急资源的布局方法。本文将通过对高速公路网中应急需求的分析,基于救援时间限制和覆盖条件建立应急设施点选址模型。

图1 路网应急需求布局图
1 路网应急需求布局及应急需求分析
研究应急设施点的布局,首先需要了解路网中可能发生交通事故的位置和在不同事故场景下的应急需求。目前,关于城市路网中事故应急需求的研究已较成熟。城市道路网中的交通事故需求点与人口数量和路网密度相关[8],即人口多、路网密度大的区域,交通事故点分布密集,相应的应急需求也较大。因此,城市路网中交通事故应急需求点按区域呈块状分布,需求点在一定区域中分布密集,如图1(a)所示。有别于城市路网,高速公路具有经济效益高、行车速度快,通行能力大等特点。高速公路交通事故具有重特大事故比率高、尾随相撞事故比率大、受气候因素影响大等基本特征[9]。高速公路网中事故应急需求点的分布与道路事故发生率、车流量和道路设施状况有关[10]。它的分布形态是沿高速公路呈线状分布,较为分散,需求点之间距离较远,如图1(b)所示。由于应急需求分布形态不同,所以城市道路网和高速公路网的应急设施点布局方法应有所区别,传统的应急资源选址模型并不适用于高速公路网中应急设施点的布局。
针对高速公路网应急需求特征,本文首先建立高速公路网络图,以直观地反映交通事故应急需求点在路网中的布局形态;然后对应急需求点进行需求分析,从而确定特定事故下需求点的应急需求情况。
1.1建立网络图
高速公路网中交通事故应急需求点的位置可以根据经验值和预测值确定[11]。经验值即为近几年发生交通事故的位置,预测值即通过车流量和道路设施等因素预测可能发生交通事故的位置[11]。用网络图来描述高速路网,可以直观地反映出交通事故应急需求点的位置和各点之间道路的连接情况,这样便于研究高速路网中应急资源的布局。网络图中用Ni表示应急需求点;用弧e表示应急需求点之间的道路连接情况。整个网络图记为G=(N,E),其中N表示点的集合,E表示弧的集合,即N={N1,N2,…, Ni},E={e12,e13,…,eij}。
1.2应急需求分析
交通事故应急需求点所需的应急资源是不确定的,这依赖于交通事故的情形、事故点所在道路的通行情况和事故对车辆通行的影响等诸多因素。本文假定交通事故情形为集合K,某种交通事故情形为k,且k∈K。为描述交通应急需求点的不确定需求,针对可能发生的交通事故情形,本文引入以下三个参数。
(1)αik表示需求点i处发生交通事故k情形的概率,根据历史资料,得到规定时间内需求点i处发生交通事故k情形的事故件数nik和需求点i处发生总交通事故的件数Nik,且:
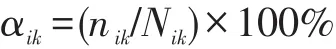
(2)Iik表示发生交通事故k情形对需求点i的影响系数,根据历史资料,得到规定时间内需求点i处发生交通事故k情形的事故件数Nik、每次发生交通事故k情形时需求点i的通行能力、需求点i的设计通行能力Qi,则:

(3)Qi表示需求点i所在路段的平均交通流量。
于是,交通应急需求点i在发生交通事故k情形下的应急需求Nik可按下式计算:

2 数学模型的建立
2.1模型假设
假设1:交通事故发生后,救援车辆从应急设施点赶往交通事故点的行程时间已知。
假设2:交通事故发生后,应急车辆通往事故点的最短救援路径不发生改变。
假设3:交通事故应急设施点的储备为耐用型物资,例如医疗箱、担架、救护车等均是可以较长

式中:I为给定公路网中交通事故应急需求点位置的集合;J为给定公路网中待选事故应急资源设施点位置的集合;Nj(k)为发生交通事故k情形时,j点在救援期限内能够提供的救援车辆数;Ni(k)为i点在发生交通事故k情形时的应急需求情况,如式(1)所示;tij为救援车辆从待选应急设施点 j到应急需求点i最短路径的行程时间(min);yij为决策变量,当i点被 j点所覆盖时,取yij=1,否则yij= 0;xj为决策变量,当在 j点设立设施点时,取xj= 1,否则xj=0;P为给定公路网所需设立事故应急资源设施点的个数;tmax为交通事故应急救援的限制期(min)。
目标函数(2)表示寻求应急资源供给能力强和救援行程时间短的最优选址情况。约束(3)表示如果待选点j覆盖了应急需求点i,则应该在j点设立应急设施点。约束(4)限制服务点设立的个数。约束(5)表示每个应急需求点i都需要被1个应急设施点j所覆盖。约束(6)表示如果j点覆盖了i点,则从j点到i点的最短路径行程时间需要在救援限制期限内。约束(7)和约束(8)定义xj和yij为0,1的整型变量。时间存放的物资。
2.2数学模型
依据以上假设,可建立如下数学模型:
3 模型算法
上述模型为线性模型,可以通过基于拉格朗日松弛的启发式算法[3]求解。将约束(5)、(6)松弛到目标函数中,设拉格朗日乘子分别为ui、λi,得到下述模型:

约束为(3)、(4)、(7)、(8)。
此模型中的拉格朗日乘子可定义为:

其中:
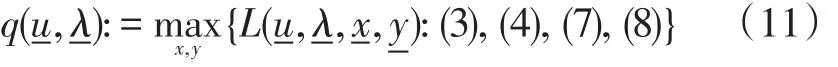
本文通过对决策变量(x,y)的求解和对松弛变量(u,l)的调整,使目标函数f和L之间不断逼近,从而得到最优解。对松弛变量的调整可以通过迭代的过程来实现,迭代方程如下:

式中:Mk和Mk+1是迭代过程中第k和k+1次的拉格朗日乘子,,αk表示第k次迭代的步长;gk表示次梯度;[]+表示松弛变量在迭代中应满足≥0且∈Rnλ,如式(13)所示:

对给定的ui和λi的值,可以求得问题L的一组可行解,将其作为最优解的上限UB。

将所有的φi相加,就可以得到选址模型最优值的下限,即LB。相应的,将满足式(9)的yij取值为1,其余取为0,就可以得到相应的1个可行解。
该模型的算法步骤如下:
(1)初始化各参数,-M0,k=1,通过式(13)求得选址模型的最优值下限LB0,通过给定的-M0求解问题L,得到最优值上限UB0;
(2)通过迭代,得到Mk,求解问题L得到最优值上限UBk;
(3)对给定的Mk,由式(13)找到选址模型的可行解计算LBk;
(4)更新最优值上下限UB和LB:

(6)更新拉格朗日乘子和迭代步长,取k=k+1,转步骤(2)。
在计算过程中,迭代步长为:
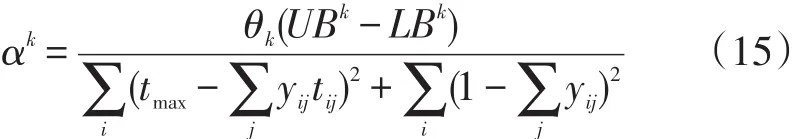
其中,参数θk初始值为2,当迭代过程中算得UBk不能更新UB时,则:

拉格朗日乘数更新如下:

4 计算实验
计划在某个区域高速公路网内设立交通事故应急救援设施点。现可以确定待选应急设施点为S= {S1,S2,S3,S4,S5,S6},已知该区域高速公路网内主要有8个交通事故应急需求点(A1,A2,A3,A4,A5,A6, A7,A8),分布情况如图2所示,需求点在交通事故k情形下的需求参数如表1所示。
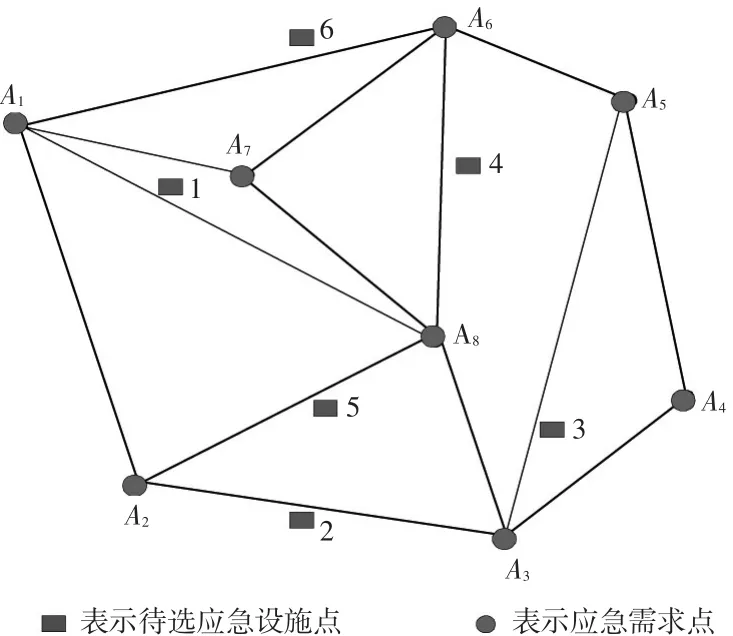
图2 需求点和待选应急设施点分布图
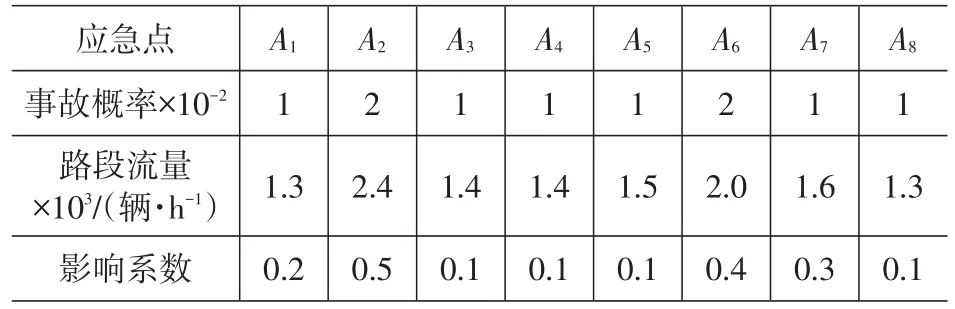
表1 应急需求点在交通事故k情形下需求参数表
应急服务点到需求点最短路径的行程时间矩阵T(min)为救援车辆从待选应急设施点(A1~A8)到应急需求点(S1~S6)最短路径的行程时间矩阵,具体为:

综合实际应急资源数量和建设资金等因素,假定救援期限为20min,则各个待选应急设施点在交通事故k情形下的应急能力如表2所示,现需从待选应急服务点中拟定3处作为应急设施点的位置。算例中应选择在待选点S1、S3、S4建立应急设施点,使得所有应急需求点被覆盖,且模型的目标函数值最大,如表3所示。

表2 应急设施点在交通事故k情形下应急期限20min内的应急能力
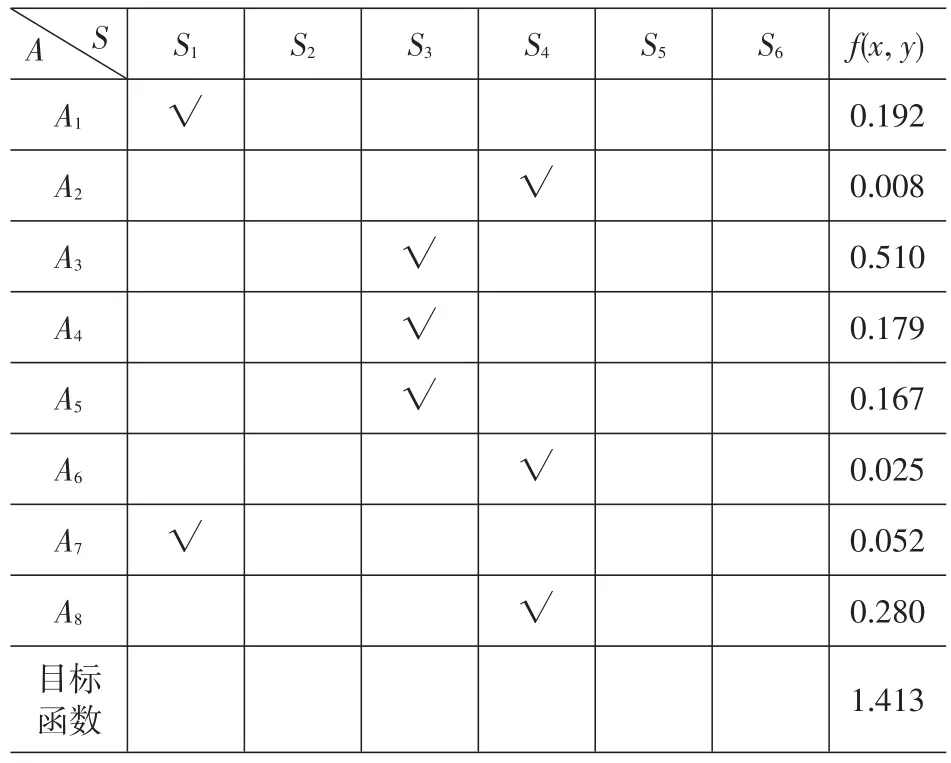
表3 利用选址模型进行选址实验得出的选址结果
5 结语
本文结合高速公路网中应急需求沿公路呈线状分布的特点,通过事故发生概率、事故影响范围和路段平均车流量三个参数分析了需求点在某个特定交通事故情形下的应急需求。对传统选址模型进行改进,考虑特定场景下存在的救援限制条件,进行交通需求应急分析,同时结合事故发生概率、事故影响情况和交通运行情况,在需求分析的基础上建立了数学模型,加入应急需求变量。
本文建立的模型以寻求应急物资供给能力强、救援行程时间短的函数为目标函数,约束条件中通过救援时间决定覆盖条件限制设施点的选址。此模型的特征是在救援时间限制条件下,需求点只被救援行程时间短、应急物资供给能力强的设施点覆盖,设施点不重复覆盖需求点,应急效率高,选址成本低。此模型属于线性模型,故采用基于拉格朗日松弛的启发式算法加以求解。将约束条件松弛到目标函数中得到新的函数,通过迭代拉格朗日乘子,使得两个目标函数不断逼近,最终得到满足迭代条件的最优解。计算实验验证了模型的可实施性,体现了该模型对高速公路网应急设施点的选址具有良好的参考价值。
总之,基于应急需求分析,考虑救援时间限制的高速公路网应急设施点选址模型,能够准确地反映应急需求特征,改变传统选址模型中以距离为选址条件,而以救援时间为选址条件并结合救援通行情况,更能契合实际救援需求。然而,恶劣天气、大型车辆等因素对实际救援通行也会产生影响,在下一步研究中,会进一步加以考虑。
[1]向红艳,张卓.高速公路交通事故紧急救援的预案生成模型[J].大连交通大学学报,2009,30(3):8-11.
[2]吴玮.公路交通安全状况及影响因素分析[D].西安:长安大学,2007.
[3]Konstantinos G Zografos,Konstantinos N Androutsopoulos. A Decision Support System for Integrated Hazardous Materi⁃als Routing and Emergency Response Decisions[J].Trans⁃portation Research Part C:Emerging Technologies,2008,16 (6):684-703.
[4]Paraskevi S Georgiadou,Ioannis A Papazoglou,Chris T Kira⁃noudis,et al.Multi-Objective Evolutionary Emergency Re⁃sponse Optimization for Major Accidents[J].Journal of Haz⁃ardous Materials,2010,178(1-3):792-803.
[5]Dian-liang Xiao,Yu-jia Tian.Reliability of Emergency Res⁃cue System on Highway[C]//International Conference on In⁃telligent Computation Technology and Automation,IEEE, Beijing,2009:564-567.
[6]Takeo Yamada.A Network Flow Approach to a City Emer⁃gency Evacuation Planning[J].International Journal of Sys⁃tems Science,1996,27(10):931-936.
[7]Hongzhong Jia,Fernando Ordóñez,Maged Dessouky.A Mod⁃eling Framework for Facility Location of Medical Services for Large-Scale Emergencies[J].IIE Transactions,2007,39(1): 41-45.
[8]Luce Brotcorne,Gilbert Laporte,Frederic Semet.Ambulance Location and Relocation Models[J].European Journal of Op⁃erational Research,2003,147(3):451-463.
[9]王建军,王军锋,毕明涛.区域公路交通事故及高速公路交通事故特征[J].长安大学学报:自然科学版,2005,25(3):66-69.
[10]Wang Yan,Guo Zhongyin.Identification of Hazardous Loca⁃tions Based on Integrated Highway Safety State Analysis[C]// Proceedings of the 9th International Conference of Chinese Transportation Professionals,ASCE,Harbin,2009:733-741.
[11]Wen Cheng,Xuesong Wang,Kekoa Anderson.How to Iden⁃tify Hazardous Locations in Roadway Network[C]//Proceed⁃ings of the 10th International Conference of Chinese Trans⁃portation Professionals,ASCE,Beijing,2010:1632-1644.
DOI:10.16503/j.cnki.2095-9931.2015.02.009
Emergency Facility Location Model of Expressway Network Within Limitation of Rescue Time
ZHAO Lin-na,DAI Shuai,GONG Jian-guo
(Road Traffic Safety Research Center of the Ministry of Public Security,Beijing 100062,China)
The emergency facility location is a key problem in the field of expressway emergency man⁃agement.A method of optimizing the emergency facility location on the expressway network by the math⁃ematical modeling was proposed.Firstly,the layout characteristics of emergency facility demand on the expressway network was analyzed,and the emergency demand under the specific traffic accident was de⁃termined in terms of the accident probability,the accident influence scope and the average traffic flow volumes.Secondly,the emergency facility location model was established based on the demand analysis. In the emergency facility location model,the facility points′coverage condition was determined by the rescue time limitation,and the facility points were chosen to build emergency facility within the condi⁃tion of rapid rescue time and sufficient rescue supplies.Finally,the method of the heuristic algorithm based on the Lagrangian Relaxation to solve this model was introduced.The emergency facility location model aimed at emergency demand on the expressway network was verified to be effective and enforce⁃able by a computational experiment,which guaranteed for the rescue time and offered a new idea for the emergency facility location.
expressway network;emergency demand;rescue limit;coverage;location model
U412.366
A
2095-9931(2015)02-0042-05
10.16503/j.cnki.2095-9931.2015.02.008
2014-10-13
“十二五”国家科技支撑计划项目(2014BAG01B04-04)
赵琳娜(1989—),女,江苏靖江人,研究实习员,硕士,主要从事道路交通安全与交通政策规划研究。E-mail:zlncg789@163.com。
