适用于继电保护的含变流器电力元件故障暂态快速仿真方法

2015-09-19申全宇宋国兵王晨清王欢欢

电力自动化设备 2015年8期

申全宇，宋国兵，王晨清，刘凯，王欢欢

（1.西安交通大学电气工程学院，陕西西安 710049；2.ABB（中国）有限公司研究中心，北京 100015）

0 引言

通过对常规电力元件的调节和控制，实现电力系统的自动化、智能化是电网运行者不变的追求。为了提高电力元件的可控性，电力电子元件在电网的发电、输电、配电以及用电环节被广泛采用[1]。电力系统分析以及继电保护均是以电力元件的数学建模和特性分析为基础的，控制系统的引入使得常规电力元件特性发生了改变。因此对含控制电力元件的建模和特性分析将无法避免。

随着新能源发电以及直流输电、交直流混合输电的发展，含变流器电力元件成为一类广泛应用的含控制电力元件。含变流器电力元件主要包含风机、光伏以及换流器，其作为一种新的电源形式，可以实现对电能的调节、变换和控制。

继电保护是电力系统安全运行的第一道防线，对快速切除故障、提高供电可靠性具有重要作用。故障特征分析是继电保护研究的前提和基础，其关键问题在于研究电源的故障响应特性。含变流器电力元件作为一种新的电源形式引入电网后，表现出许多异于传统同步机电源的故障特征，有必要从继电保护角度对其故障特性进行研究分析。

目前对于含变流器元件故障特性的研究主要基于仿真结果分析。变流器的仿真精度决定了数字仿真对实际物理系统模拟的可信度，对含变流器系统暂态仿真研究有着直接影响；变流器的仿真速度则是评价暂态仿真方法实用性的重要指标之一，尤其是在含大规模变流器的电力系统中，变流器的仿真速度直接关系到整个系统的仿真性能。因此，有效性和快速性是评价变流器模型优劣的2个指标。

国内外已经开展了许多关于变流器仿真模型的研究，其基本上可以归为以下几类。

a.详细模型[6]。该模型完整复现了变流器的实际拓扑结构，与物理模型完全一致。但由于变流器结构复杂，模型比较庞大，仿真计算量随着系统规模成指数倍增长，严重制约系统的仿真速度。

b.开关函数模型[6-11]。该模型仅关注变流器的外部特性，减少了仿真计算量，提高了仿真速度，且开关函数的引入保留了变流器输出中的高频分量，但开关动作时刻的计算仍然需要较大的计算量。

c.平均值模型[5-6，11-12]。该模型考虑变流器的输入、输出特性，仅保留其输出中的低频分量，大幅减少了变流器仿真计算量，可以有效地提高含变流器系统的仿真速度。

由以上分析可知，平均值模型虽然只能获得变流器输出的低频分量，但可以大幅提高其仿真的速度。考虑到目前电力系统二次侧大都包含滤波环节，高次谐波将会被滤掉，一般只能获取系统的低频分量；同时目前现场运行的继电保护装置普遍采用工频量保护，主要关心工频分量的暂态变化过程。因此，采用平均值模型对变流器故障暂态进行简化建模，在保证变流器仿真精度的条件下，提高其数字仿真的速度，尤其是实现风电场、光伏电站等大规模含变流器系统的快速仿真，对含变流器系统的继电保护研究具有重要意义。

本文针对含变流器电力元件输出的工频故障暂态分量，给出一种适用于继电保护的平均值模型。该模型忽略变流器细微的内部结构，将其等效为一个可以实现交、直流间电能转换的受控元件，从能量平衡角度出发，兼顾其控制特性，对含变流器电力元件整体进行简化数学建模，以微分方程组代替变流器详细模型的搭建，避免在仿真过程中大量使用电力电子元件，精简仿真模型复杂程度，大幅减少变流器环节的仿真计算量，提高仿真速度，实现风电场等大规模含变流器系统的快速暂态仿真。PSCAD仿真结果验证了本文方法的有效性和快速性。

1 变流器功能与控制策略分析

1.1 变流器功能分析

变流器完整拓扑结构如图1所示，其基本结构主要为电力电子开关元件组成的主电路和采用特定控制策略的控制电路两部分。

图1 变流器完整拓扑结构图Fig.1 Complete topology of converter

忽略变流器内部复杂的结构，可以将其简化为图2所示电力元件。

图2 变流器简化拓扑结构Fig.2 Simplified topology of converter

变流器功能具体分析如下。

a.电能变换。变流器主电路相当于一个电能变换器，沟通交、直流系统，其主要功能为实现交、直流间电能的变换与传递。因此当忽略变流器内部功率损耗时，变流器两侧功率应保持平衡。

b.特性受控。控制电路采用特性的控制策略，实现对电能变换传递过程的调节与控制。因此，含变流器电力元件的暂态响应特性主要受控于控制策略和控制参数。

1.2 变流器控制策略分析

目前变流器普遍采用基于定向矢量的控制原理。该原理采用双闭环控制，可以提高变流器静态性能，降低电流对变流器参数的敏感程度，增强电流系统鲁棒性[3]。

变流器定向矢量控制策略一般在两相旋转坐标系下进行，将d轴定向于交流侧电压矢量，即uq=0，此时交流侧在dq坐标下的功率表达式可以表示为：

由式（1）可知，交流侧有功功率只与id有关，无功功率只与iq有关，从而在dq坐标下实现了有功和无功的解耦控制，其典型控制策略框图如图1所示。对其控制特性进行分析，可以得到如下结论。

a.典型变流器控制策略分为有功和无功两部分。

b.有功部分一般采用双闭环控制，通常分为电压外环和电流内环。

c.直流电压外环主要用于稳定直流侧母线电压，并得到有功电流参考指令；电流内环主要用于快速跟踪电流参考指令，提高控制系统的动态响应特性。

d.有功电流内环需要跟踪电压外环，其调节速度一般远快于电压外环，因此有功电流控制特性主要取决于直流电压外环。

e.无功电流一般采用直接电流控制，响应特性取决于自身比例-积分（PI）调节器的控制参数。

2 变流器简化数学模型

基于上述对变流器功能与控制策略的分析，从继电保护角度，针对其工频输出响应，忽略变流器内部电力电子变换元件的细微结构，可以得到含变流器电力元件的简化数学表达式，实现对其故障暂态的快速仿真。具体数学模型推导方法如下。

含变流器电力系统简化模型如图3所示。图中，C为直流侧稳压电容；udc为直流侧电压；Pdc为直流侧系统输入变流器功率；uabc为交流侧变流器端口的三相对地电压；iabc为输入交流系统的三相电流。

图3 含变流器系统简化模型图Fig.3 Simplified model of system with converter

变流器功能为实现电能的转换与传递，由变流器两侧有功功率守恒可以得到：

其中，ud为dq坐标下uabc的d轴分量；id为dq坐标下iabc的d轴分量；r为变流器开关损耗等效电阻，与开关通态电阻值相关。

变流器控制策略分为有功和无功两部分。

有功电流控制特性取决于直流电压外环，其数学表达式为：

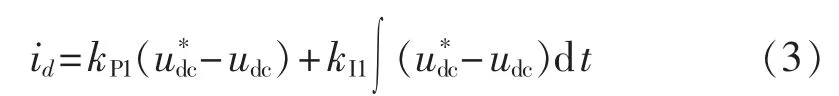
其中，kP1和kI1分别为有功电流PI调节器的比例、积分参数；ud*c为直流母线电压指令。

无功电流特性取决于自身PI控制参数，其数学表达式为：

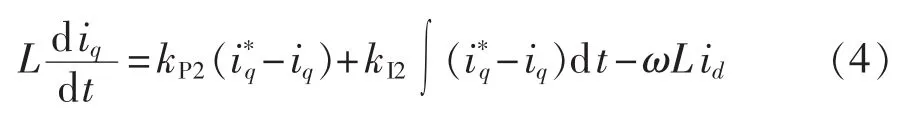
其中，kP2和kI2分别为无功电流PI调节器的比例、积分参数；iq*为变流器输出无功电流指令；L为交流侧滤波电感；ω为工频电角频率。

进一步考虑变流器自身过流保护，流过变流器的电流不得超过其最大允许电流。

其中，imax为变流器输出电流允许最大值。

将式（2）—（5）联立起来即得到了变流器简化数学模型表达式。该数学模型将变流器等效为交、直流间电能转换元件，兼顾变流器控制策略，保留了变流器的功能与控制特性，体现了控制策略以及控制参数对变流器暂态响应的关键作用，反映了含变流器电力元件的故障暂态响应特性。由于上述模型在dq坐标下推导得到，因此，该模型忽略了由于电力电子开关引入的高次谐波，反映了变流器输出工频分量的故障暂态响应。

为了将上述模型写入PSCAD仿真软件，需要对其进行离散化，得到变流器输出响应迭代格式。

对式（2）—（5）联立的方程组进行离散化处理，并进行数学变形，可以得到变流器输出响应直流电压udc和交流电流id、iq的离散迭代格式：

其中，Ts为仿真步长；k=1，2，…，N，N 为采样点数。对idq进行反Park变换，可以得到静止坐标下变流器输出三相电流iabc。

其中，θ0为d轴与a轴之间的夹角。

联立式（6）、（7）即可得到含变流器电力元件的简化数学模型离散表达式。式（6）仅保留了对变流器暂态特性至关重要的部分，精简变流器模型的复杂程度，采用离散微分方程交替迭代求解变流器输出工频分量的数值解，大幅减小了变流器暂态响应的计算量，从而提高了系统的仿真速度。将上述离散数学模型写入PSCAD仿真软件，即可实现含变流器电力元件故障暂态的快速仿真。

3 仿真验证

在PSCAD仿真软件上搭建含变流器系统的详细仿真模型，针对其交流系统侧故障后的故障暂态响应，与本文提出的变流器简化模型仿真结果进行对比，验证本文方法的有效性；同时，采用全功率变流器型永磁直驱风电系统，通过比较在相同风机台数、相同的仿真时间长度下，详细模型与简化模型所需时间，验证本文方法的快速性。

3.1 简化模型有效性验证

在PSCAD上搭建图4所示含变流器系统的详细仿真模型，图中，整流器和逆变器采用背靠背连接，uabc为逆变器出口对地三相电压，iabc为流入逆变器的三相电流，udc为直流母线电压，F为故障点。

图4 含变流器系统的详细仿真模型Fig.4 Detailed simulation model of system with converter

由于直流环节的隔离作用，故障后变流器输出响应主要取决于逆变器，整流器仅起到电能变换与传递的功能。逆变器具体参数为：直流电压比例增益KP1=2.0，直流电压积分增益KI1=0.01；无功电流比例增益KP2=5.0，无功电流积分增益KI2=0.0002；交流侧滤波电感L=0.002 H，直流侧稳压电容C=0.01F，变流器开关损耗等效电阻r=0.08ω。

1.5s时F点故障发生电压跌落，以下针对对称故障和不对称故障2种情况分别进行仿真验证，其中仿真步长Ts=0.1 ms。

a.含变流器系统交流侧对称故障。逆变器交流侧出口电压从0.58 kV跌落到0.3 kV，故障暂态仿真结果对比如图5所示，图中纵轴均为对应电压、电流的幅值，后同。

从图5中可以看到，当逆变器交流侧发生故障后，直流侧部分功率由于无法向交流侧输送而堆积在直流母线上，使得直流母线电压升高，由于控制回路的调节作用，经过故障暂态过程后直流电压恢复正常；交流侧电流经故障暂态上升到稳态值，其暂态响应特性取决于控制电路。同时，在三相对称故障后的变流器故障暂态过程中，简化模型仿真直流母线电压以及输出电流在故障暂态和故障稳态下均能够很好地吻合详细建模仿真结果，这说明了简化仿真模型的有效性。

图5 对称故障下简化模型与详细模型仿真结果对比Fig.5 Comparison of simulative results between simplified and detail models for symmetric fault

b.变流器系统交流侧不对称故障。变流器交流侧经过渡电阻发生bc相间故障，故障暂态仿真结果对比如图6所示。

从图中可以看出，发生不对称故障时，交流侧负序分量的存在导致变流器直流母线电压和输出电流中引入了2次谐波分量，因此故障后其波形会有一定的波动，但其变化规律与对称故障相同；同时简化仿真模型与详细模型仿真结果几乎完全重合，进一步说明了简化仿真模型的有效性。

以上不同故障类型下含变流器系统的仿真对比验证结果，有效地说明了简化模型适用于含变流器系统的故障暂态仿真，可以作为内部结构复杂的含变流器电力元件的一种简化仿真模型。

3.2 简化模型快速性验证

风电场是目前含变流器最多的系统，其快速仿真是目前研究的难点。采用本文的简化模型仅对直驱风机变流器部分进行简化，其他部分保持不变的情况下，分别针对包含1台直驱风机、2台直驱风机以及3台直驱风机的风电系统，在1台主频为2.5 GHz电脑上进行仿真，仿真时间为5s，仿真步长为0.1 ms。对比简化模型和详细模型仿真所需时间，定量地验证本文方法的快速性及其在风电场等大规模含变流器系统应用的可行性。对比结果如表1所示。

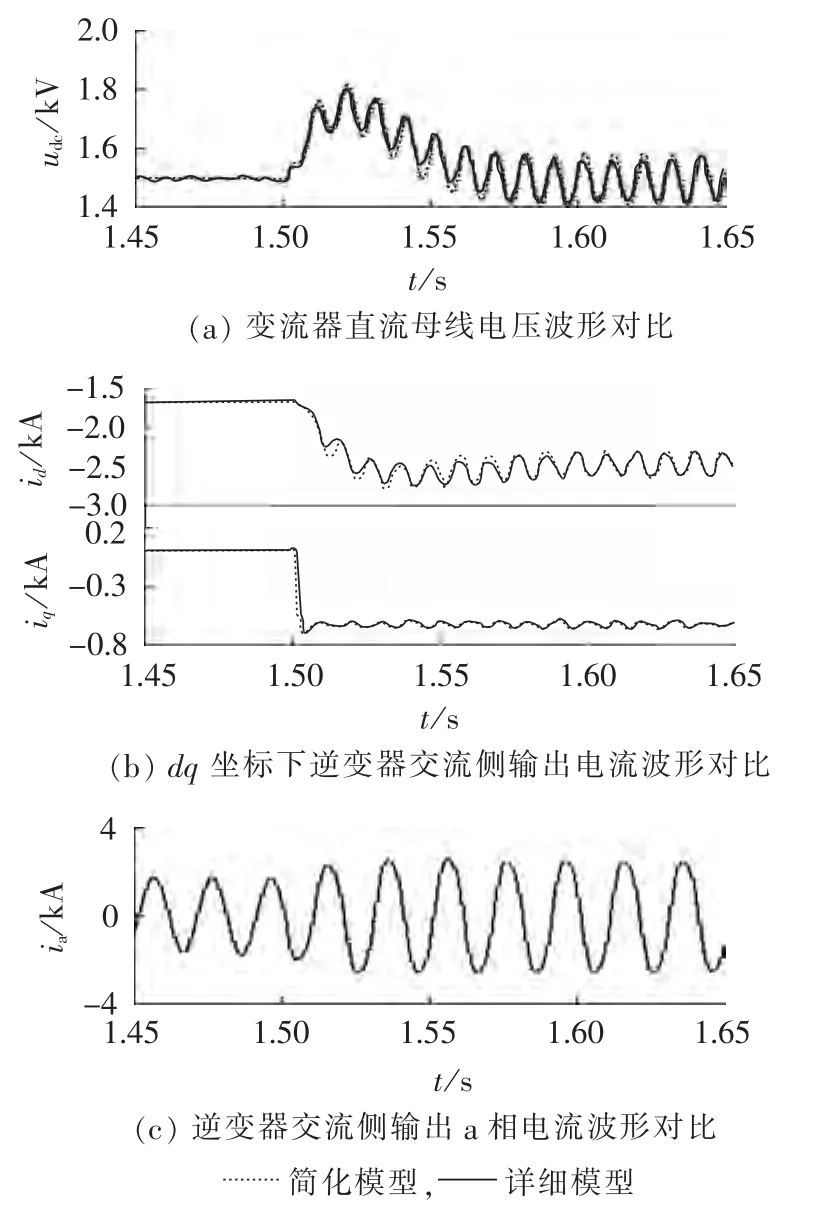
图6 bc相间故障下简化模型与详细模型仿真结果对比Fig.6 Comparison of simulative results between simplified and detail models for b-c interphase fault

表1 简化模型与详细模型仿真时间对比Table 1 Comparison of simulation time between simplified and detail modes

从表1中可以看到，详细模型所需时间随着系统规模成指数倍增长，当系统包含3台风机时，详细模型需要1332s进行5s的仿真，对于包含几百台风机的大型风电场，采用详细模型仿真根本无法实现；简化模型仿真则受系统规模影响很小，随着系统规模增大，所需时间增加很少。2种仿真模型仅变流器部分不同，所需时间的巨大差异说明了变流器部分是制约大规模含变流器系统仿真速度的主要原因，同时也验证了本文简化模型仿真方法的快速性，说明了该方法可以用于风电场、光伏电站等大规模含变流器系统的故障暂态仿真。