基于改进的Benders分解与透视割平面的机组组合算法

郑海艳，简金宝，全 然，杨林峰

（1.广西大学 数字与信息科学学院，广西 南宁 530004；2.玉林师范学院 数学与信息科学学院，广西 玉林 537000；3.河南工业大学 理学院，河南 郑州 450001；4.广西大学 计算机与电子信息学院，广西 南宁 530004）

0 引言

在当今节能减排这样一个世界共识下，电力系统的优化运行显得尤为重要。机组组合UC（Unit Commitment）是电力系统运行调度一个非常重要的方面，同时也是一个非常活跃的研究领域。近年来各类UC问题相继被提出和研究，如融入随机性很强的风能发电的含风电场的UC问题[1]、含插电式混合动力汽车的UC问题[2]等，然而火电机组仍然是最主要的组成部分。经典的UC问题是指在一个调度周期内满足系统负荷需求和旋转备用等条件下，确定机组的启停计划和机组出力，从而使得发电总费用最小，其在数学上是一个大规模的混合整数规划问题。由于其可行解集的组合性质，UC问题是一个NP（Nondeterministic Polynomial）难问题，即在多项式时间内很难求解。到目前为止，尝试用于求解UC问题的方法大致有确定性和启发式两大类。确定性方法主要有动态规划法[3]、割平面法[4]、半定规划法[5]、拉格朗日松弛法[6]和外逼近法[7]等；启发式方法主要有遗传算法[8]、禁忌搜索[9]和粒子群算法[10]等。 在上述方法中，启发式方法可以很好地处理离散变量，在理论上也具有全局收敛性，但由于是随机搜索方法，其计算效率不稳定，且容易陷入局部最优解。在确定性方法中，拉格朗日松弛法根据对偶理论将大规模问题分解为多个易于求解的中小规模子问题，是目前求解大规模UC问题最有效和最常用的方法之一。但由于对偶间隙的存在，该方法难以获得UC问题的全局最优解，且在迭代过程中容易出现振荡现象。

Benders分解法 BDM（Benders Decomposition Method）[11-12]是求解组合优化问题的一类经典方法，其基本思想是将问题分解为相对易于求解的主问题和子问题，通过逐次交替迭代求解主问题和子问题来达到求解原复杂问题的目的。传统的BDM中主问题是一个混合整数线性规划问题，其求解比较费时，文献[13]提出一个基于分支割平面的内点型BDM，算法中求解的是主问题的线性松弛，并且证明了由此所产生的松弛型Benders割平面是全局性的有效割平面。

为了改进传统BDM的计算效率，本文基于文献[13]的思想，首先结合覆盖不等式建立一个求解离散变量为0-1变量的混合整数规划的改进的松弛型BDM；其次，对于经典的UC问题，本文借助于透视割平面（PC）和线性化技术建立一个新的近似混合整数线性规划MILP（Mixed Integer Linear Programming）模型；最后利用本文所建立的改进的松弛型BDM求解该近似MILP模型。由于改进的松弛型BDM的主问题是一个线性规划问题，且中间加入了大量的覆盖不等式，整个算法的计算效率大幅提高。10～1000台机组24时段多个系统上的测试结果表明，相比于传统的BDM，本文算法的计算时间大幅减少。另一方面，将测试结果与其他方法进行比较，结果进一步说明了本文算法是有效的。此外，本文算法可顺利推广应用到求解其他类型的UC问题中。

1 BDM与覆盖不等式

1.1 BDM 简介[13]

BDM是一种分解方法，其思想是将复杂问题分解为2个相对简单的形式，即主问题与子问题，初始主问题是原问题的一个松弛，仅包含部分约束和变量，而在子问题中，主问题中已经考虑过的变量的值可以固定下来。以如下形式的MILP问题为例：

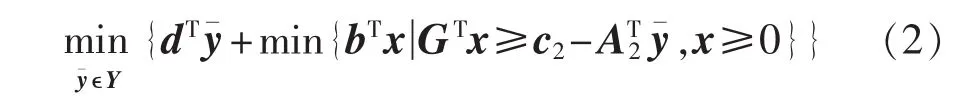
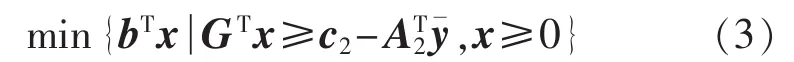
常称为原始子问题，其相应的对偶子问题为：

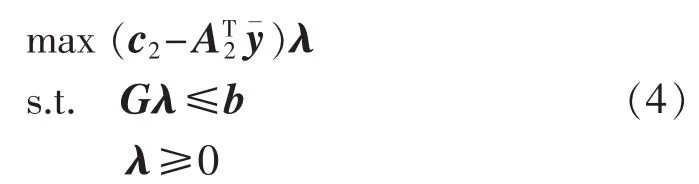
注意到对偶子问题（4）的可行解集与整数变量y无关，且根据对偶理论（2）可表示为：

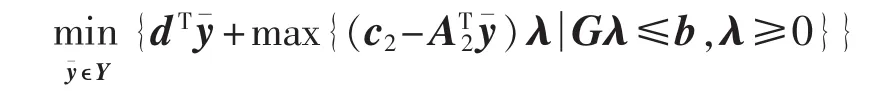
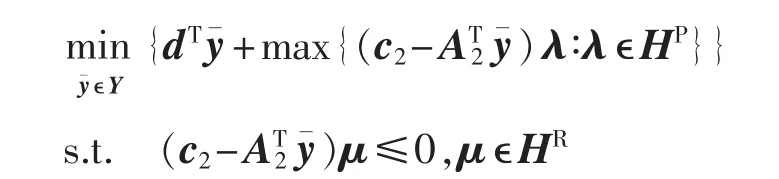
引入一个辅助变量θ，将上述问题进一步表示为：

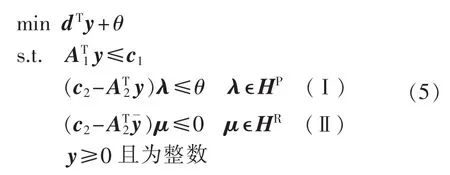
式（5）称为 Benders主问题，约束（Ⅰ）、（Ⅱ）分别称为Benders最优性割平面与可行性割平面。在Benders算法的具体实施过程中，通常是从HP与HR均为空集开始，然后在迭代过程中不断更新这2个集合。算法中Benders最优性割平面是通过求解原子问题（3）或对偶子问题（4）产生，而 Benders 可行性割平面可通过求解另一可行性子问题来产生。若y为0-1变量，文献[19]提出了可显式计算产生的组合Benders割平面，即下述整数型割平面：

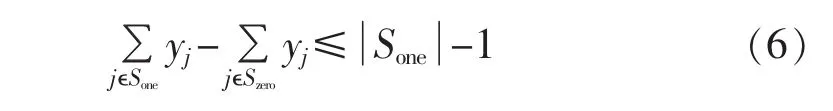
1.2 覆盖不等式[4]

对于整数规划问题所有的可行解而言均成立的不等式称为有效不等式，进一步若其对于整数规划松弛问题的可行解而言，并不是处处成立，则称其为割平面。下面介绍一类非常有用的有效不等式——覆盖不等式，其能非常有效地割除连续松弛问题最优解中整数变量的非整数值。以如下0-1背包问题为例：

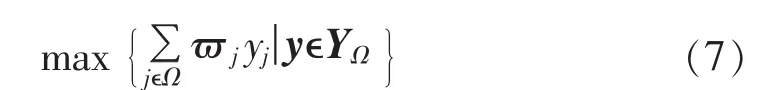
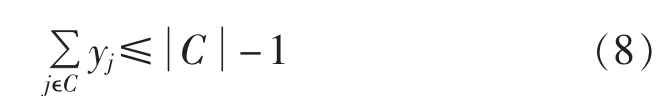
为可行集YΩ的一个覆盖不等式，其中表示集合C中元素的个数。

定理 1[4]：设 C⊆Ω为 0-1背包约束的一个覆盖，则覆盖不等式（8）为0-1背包问题（7）可行解集YΩ的一个有效不等式，同时是一个割平面。

2 UC问题的数学模型

为方便起见，先引进一些记号：N为机组总数，机组标号 i=1，2，…，N；T为时段总数，时段标号 t=1，2，…，T；αi、βi、γi为机组 i的发电费用参数；Chot，i、Ccold，i分别为机组i的热启动费用与冷启动费用；分别为机组i的最小停机时间与最小运行时间；Ti，t为机组i在第t时段已连续运行时间（为正值）或连续停机时间（为负值）；Tcold，i为机组 i的冷启动时间；PD，t为系统第 t时段的总负荷分别为机组 i的最小和最大出力；Pup，i、Pstart，i、Pdown，i、Pshut，i分别为机组i的功率上升速度限制、启动功率速度限制、功率下降速度限制及停机功率速度限制；Rt为系统第t时段的总备用。0-1整数变量ui，t为机组i在第t时段的状态，值为1表示机组i处于运行状态，值为0表示机组i处于停机状态；连续变量Pi，t为机组i在第t时段的出力。经典UC问题的目标函数为发电总费用FC最小，即：

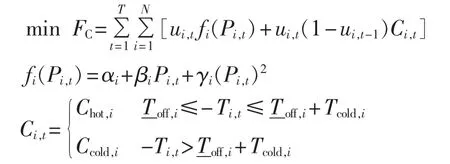
其中，fi（Pi，t）为机组 i在第 t时段的发电费用，常用二次函数表示；Ci，t为机组i在第t时段的启动费用。

UC问题的约束条件如下。

a.功率平衡约束：

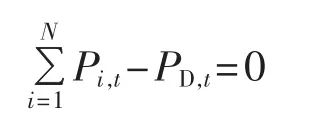
b.机组出力约束：

c.爬坡约束：

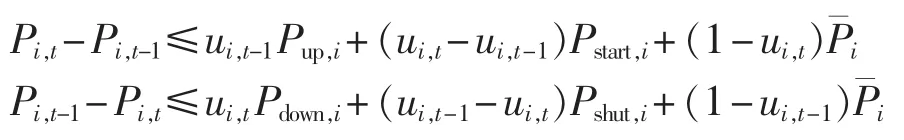
d.旋转备用约束：

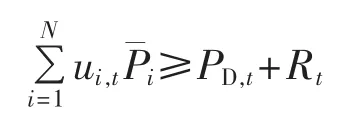
e.最小启停时间约束：

3 基于改进的松弛型BDM与透视割平面求解UC问题

3.1 改进的松弛型BDM

传统BDM中的主问题是一个MILP问题，求解比较费时，其求解时间占用整个算法的绝大部分，为改进传统BDM的计算效率，文献[13]提出一个基于分支割平面的内点型BDM。基于文献[13]的松弛思想，本文结合覆盖不等式建立一个求解0-1 MILP问题改进的松弛型BDM。下面给出改进的松弛型BDM的基本步骤。

（1）初始化：给定初始上界UB与下界LB、允许误差。

（2）当 LB＜UB-ε 时，执行下列步骤。

步骤1：求解主问题（5）的线性松弛得到 y¯，同时利用式（5）的目标函数值修正下界LB。

步骤2：利用y¯产生相应的覆盖不等式。

步骤3：利用 y¯形成相应的子问题（4）并求解。若子问题有解，则产生松弛型Benders最优性割平面（I），同时更新HP，若子问题的解进一步满足整数要求，则修正上界UB；若子问题无解，则利用式（6）计算组合Benders割平面。

步骤4：将所产生的覆盖不等式以及Benders割平面加入到主问题（5）中，返回步骤1。

引理 1[13]改进的松弛型BDM步骤3中所产生的Benders割平面是全局性的有效割平面。

3.2 UC问题的近似MILP模型

在文献[15]中，Frangioni与 Gentile针对一类凸的具有特定结构的0-1混合整数规划提出一类特殊的有效不等式——透视割平面。文献[16]将其进行了推广，通过引进0-1变量将一类更具一般性的混合整数非线性规划问题进行透视变形。为简单起见，同时结合UC问题的特点，以如下形式的混合整数规划为例简单介绍透视割平面：

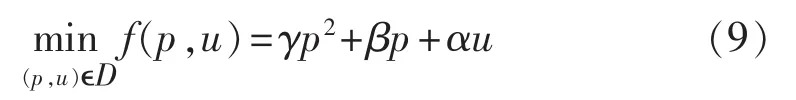
其中，D= [0，0]∪[pmin，pmax]×｛1｝，常数 pmin≤pmax；γ、β、α为常数系数。问题（9）最好的凸松弛就是计算f（p，u）在D上的凸包络，即求解定义在其最小上图像上的闭凸函数。 记 f（p，u）的闭凸包为 h（p，u），即：

显然 h（p，u）与透视函数 g（p，u）=uf（p，u）相关，且当（p，u）ϵD 时，由 0＜u≤1 知 h（p，u）≥f（p，u）。 所以对于连续松弛方法而言，作为目标函数h（p，u）比f（p，u）更好，但是 h（p，u）最大的一个缺陷就是非线性程度高，且在（0，0）处不可微。 根据文献[15]中的定理1可知函数h（p，u）的上图像是由满足以下2个条件的（z，p，u）组成：

a.upmin≤p≤upmax，0≤u≤1；

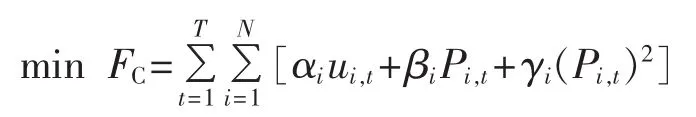
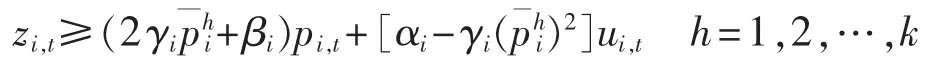
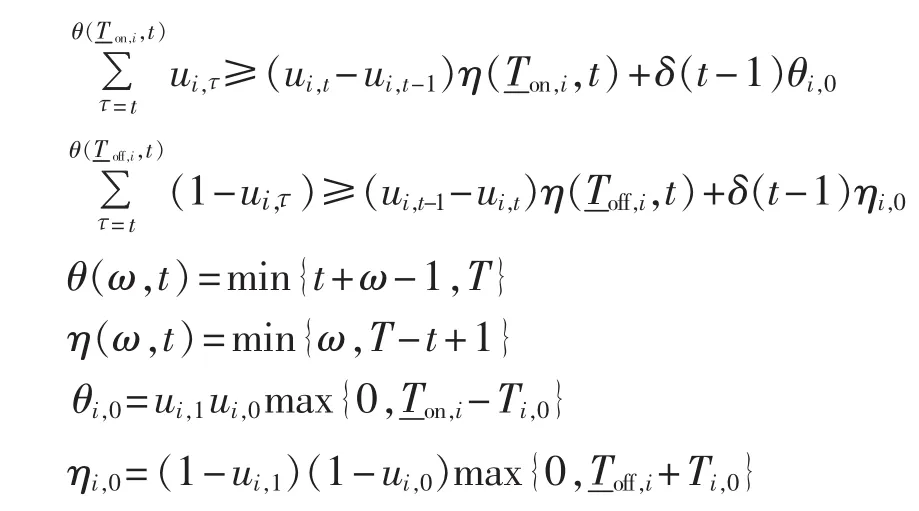
基于以上分析，将UC问题近似写成如下MILP模型：

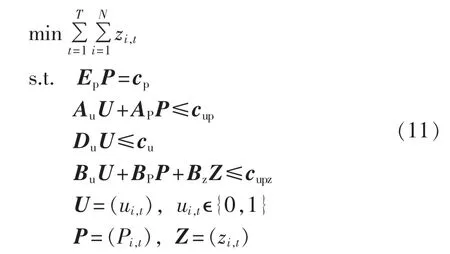
其中，EP、Au、AP、Du、Bu、Bp、Bz为相应系数矩阵；cp、cup、cu、cupz为常数向量。

3.3 MILP模型的求解

由于UC问题中的旋转备用与最小启停时间约束仅含整数变量，且根据0-1变量值的互补性，很容易将其写成0-1背包约束的形式，从而可以利用文献[4]中的启发式方法产生相应的覆盖不等式。利用透视割平面以及线性化技术将UC问题近似表示为MILP模型后，利用3.1节所建立的改进的松弛型BDM进行求解。松弛型BDM在求解UC问题的过程中整个问题被分解成主问题与子问题两部分，其中主问题仅涉及到与机组启停状态相关的变量和一个简单的连续变量，即：

利用主问题所得到的U，形成如下原始子问题：

求解该子问题或其对偶子问题可得到相应的松弛型Benders最优性割平面，而当子问题无解时则利用式（6）产生相应的整数型割平面。当精度满足算法终止时，整数要求并不满足，则可采用文献[4]中的方法，进行一些启发式调整。图1给出具体的算法流程图。

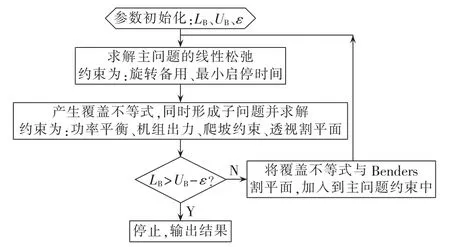
图1 算法流程图Fig.1 Flowchart of algorithm

4 数值仿真

为说明所提算法的有效性，在10～1000台机组24时段等多个系统上进行测试，其中10台机组的发电机参数及各时段负荷数据见文献[6]。20～1000台机组的相关数据是通过复制10机组24时段系统的基本参数得到。旋转备用取系统总负荷的10%。运行环境为AMD Athlon Dual Core Processor 4400+2.3 GHz，1 GB RAM，并在 MATLAB 2009a环境下调用 CPLEX 11[17]求解主问题与子问题。

算法中各参数的取值如下：允许误差ε=0.005；初始上、下界分别为UB=∞、LB=0。此外，在形成透视割平面时取。

为了说明改进的松弛型BDM比传统的BDM计算效率高，对于不计爬坡约束情形，分别将这2种算法对10～1000台机组进行测试。2种算法的迭代次数均为2次，其他测试结果具体见表1，其中BDM表示用传统的Benders分解求解UC问题新的近似MILP模型，RBDM则表示用改进的松弛型Benders分解进行求解。从表1可以看出，2种算法所计算得到的发电总费用基本相近，但计算时间方面，RBDM却少了许多，RBDM的计算时间不到BDM的一半。

表1 10～1000台机组系统24时段的测试结果（无爬坡约束）Table 1 Test results of 24-period，10～1000-unit systems（without ramp-rate constraint）

另一方面，由于广义Benders分解（GBD）可直接用于求解混合整数非线性规划问题，文献[14]直接利用GBD求解UC问题。为了与文献[14]中的计算结果进行比较，下面对于40～100台机组不计爬坡约束，并且采用相同的允许误差进行测试，比较结果见表2，表中“—”表示文中没有给出结果。通过表2可以看出，除了误差为0.004时40台机组与100台机组的测试结果比GBD方法稍差外，本文所提算法的其他计算结果均优于文献[14]中GBD方法的计算结果。此外，在求解不同规模UC问题时文献[14]中GBD方法的迭代次数为3～5次，而本文算法则均为2次，说明本文算法具有良好的稳定性。

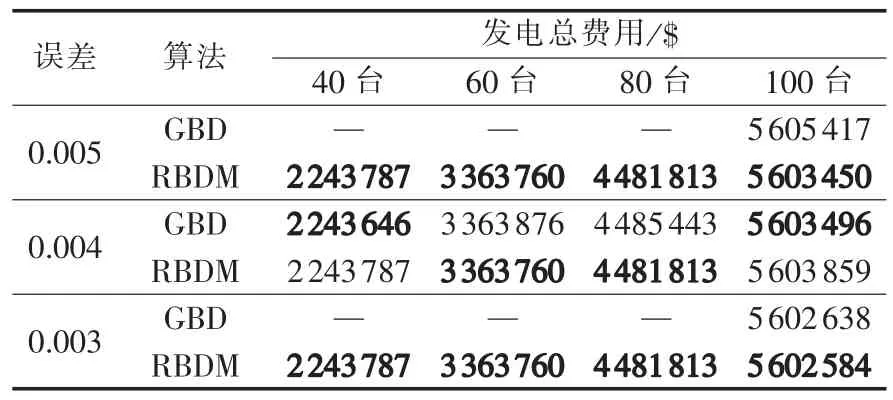
表2 40～100台机组系统24时段2种算法的结果比较Table 2 Comparison of test results between two algorithms for 24-period，40～100-unit systems

为了进一步检验本文所提算法的有效性，对于10～100台机组不计爬坡约束情形，再将计算得到的发电总费用和文献[6]与文献[18]的方法进行比较，其中文献[6]是采用拉格朗日松弛法求解UC问题，而文献[18]是把UC问题近似表示为MILP模型，然后直接调用CPLEX进行求解。在相同的条件下将计算结果进行比较，具体见表3。通过表3可以看出，本文算法的计算结果均优于另外2种方法的计算结果。

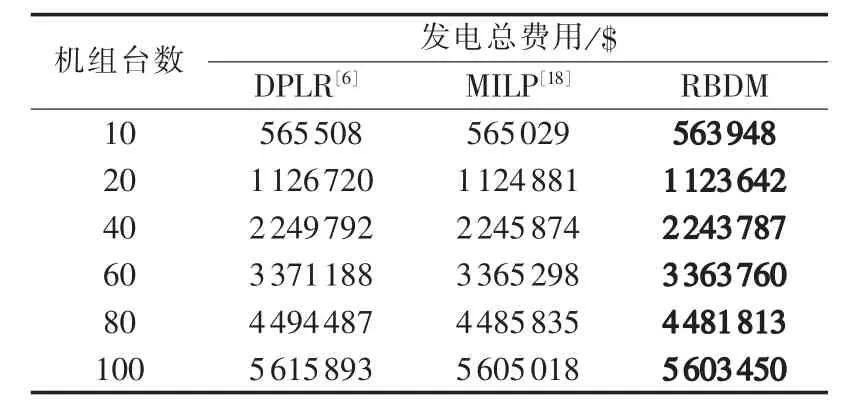
表3 10～100机组系统24时段不同算法的结果比较Table 3 Comparison of test results among different algorithms for 24-period，10～100-unit systems

对于计及爬坡约束情形，类似于文献[4]，取机组爬坡约 束功率限制分别 为 Pup，i=Pdown，i=20%Pi，且不计启动和停机功率速度限制，令 Pstart，i=Pshut，i=Pi。 用传统的BDM和本文所提出的RBDM这2种方法对10～100台机组进行测试，测试结果也是2种算法都经过2次迭代收敛，计算所得的发电费用基本相近，而RBDM的计算时间却大幅减少，具体结果如表4所示。

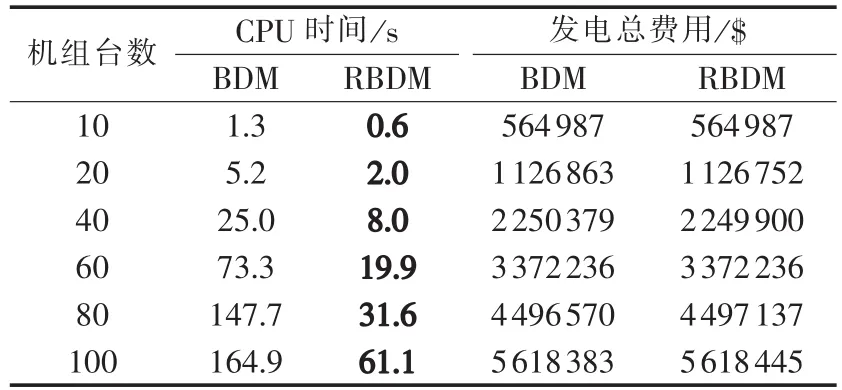
表4 10～100机组系统24时段结果（计及爬坡约束）Table 4 Test results of 24-period，10～100-unit systems（with ramp-rate constraint）

5 结语

本文基于改进的松弛型BDM与透视割平面，提出一种求解UC问题的新算法。该算法通过借助覆盖不等式建立一个改进的松弛型BDM，算法中大量覆盖不等式的加入与线性松弛大幅减少了计算时间。10～1000台机组24时段多个系统的数值仿真结果也证实了本文算法能在较快的时间内获得高质量的次优解。该算法为各类UC问题的有效求解提供了一条新的途径。