基于模糊层次分析法的项目优先级评定方法及应用
2015-09-19王锐鑫沈国荣
王锐鑫,肖 峰,沈国荣,杨 宇
(苏州长风航空电子有限公司,江苏 苏州 215151)
基于模糊层次分析法的项目优先级评定方法及应用
王锐鑫,肖 峰,沈国荣,杨 宇
(苏州长风航空电子有限公司,江苏 苏州 215151)
近年来,多项目管理已日渐成为项目管理学研究的重点,而如何确定项目优先级作为多项目管理的关键环节,也日渐凸显其重要性。在有限资源的条件下,多项目并行,合理并科学地评定项目的优先级,能大幅度减少项目间的冲突,并为项目资源分配、计划安排提供科学的依据。通过结合前人提出的指标集,根据项目管理自身的特点,建立包括学习与创新能力、内部经营过程、财务、客户满意度4个单元的多级指标多因素评价系统,达到了定量评价项目优先级的目的。实例表明,采用模糊层次分析法(FAHP)来综合评价项目优先级,适用性较强,计算结果稳定、客观,且简便实用。
多项目管理;模糊层次分析法;指标系统
1 基于模糊层次分析法对项目优先级进行评定
1.1基本理论
著名的美国运筹学家Saaty在20世纪70年代提出一种定量与定性结合、层次化、系统化的分析方法,被称为层次分析法(AHP)。该方法为项目管理中多约束的决策问题提供了大力支持。应用层次分析法包括3个步骤:第一,判断矩阵的确定;第二,判断矩阵各元素相对权值和综合权值的确定;第三,对评价指标和评价函数赋值。传统层次分析法也有明显的缺陷,由于多种评价指标无法量化,通常采用自然语言来强调指标的重要度。而模糊层次分析法(以下简称FAHP)是运用模糊数学的方法量化评价指标,充分考虑思维的模糊性,将传统层次分析法与模糊理论相结合的理论方法。
1.2建立多项目优先级的评价指标系统
合理的项目优先级评价指标系统应考虑如下几方面:第一,对组织及员工学习与创新能力的提升;第二,对企业内部经营过程的提升;第三,对顾客满意度的提升;第四,项目的财务回报;第五,项目的风险控制等方面的因素。
设计评价指标时应遵循灵活性、动态性、定性分析与定量分析相结合、系统性、可比性和可测性、相对独立性等原则。通过借鉴关键成功因素和平衡记分卡的思想,采用分组讨论和问卷统计相结合的方法,建立评价指标系统。
1.2.1学习与创新能力
学习与创新能力强调员工与组织不断学习、创新的能力,以保证企业未来的发展空间和竞争力。项目对企业有直接与眼前的回报(财务等),同时也要有间接和长远的回报,项目要与企业一起发展,为企业发展服务。有关学习与创新能力的二级指标如下。第一,企业核心竞争力是否增强;第二,员工创新性是否提升。该指标用来衡量团队成员是否可以本项目为契机,在管理创新、技术创新、思维创新上取得进步。第三,员工满意水平。
1.2.2组织内经营过程
项目结项后是否提升管理能力,是否提升组织内的技术水平,多项目管理的内部经营评价都会有所体现。有关组织内部经营过程的二级指标如下。
第一,实施该项目对组织内整体技术水平提高的促进;第二,实施该项目对企业内协调能力提升的促进;第三,实施该项目对企业内管理水平提升的促进。
1.2.3顾客满意指标
顾客对项目开展过程的满意度,包括在项目实施过程中的满意度以及项目能给顾客带来的经济收益。只有顾客满意才能拓展市场,并使顾客获利。有关顾客满意度的二级指标如下。
第一,实施该项目的潜在市场是否很大,是否会拥有更多顾客;第二,顾客对所提供服务的满意程度。
1.2.4财务收益
财务收益情况直接与企业战略目标衔接,并能直接反映企业的经营状况。在对多项目优先级评价的过程中,需重点考虑这些项目对企业经济收益的情况,假如某项目能给企业带来很好的财务收益,相应地,在资源分配过程中也应有所倾斜。有关财务收益的二级指标如下。第一,实施该项目所产生的社会效益。该指标是实施该项目对国民经济产生的收益。第二,实施该项目所产生的净现值。该指标是指项目中流入资金与流出资金的差额,是项目开展过程中的净收益。第三,实施该项目所需资金的利润率。该指标表明了项目获利情况。项目的利润率越高,企业收益越好。第四,实施该项目所需投资总额。该指标表明项目规模,投资规模越大的项目相应也需要越多的资源配置。
综上所述,可得到多项目优先级评价指标系统,如图1所示。
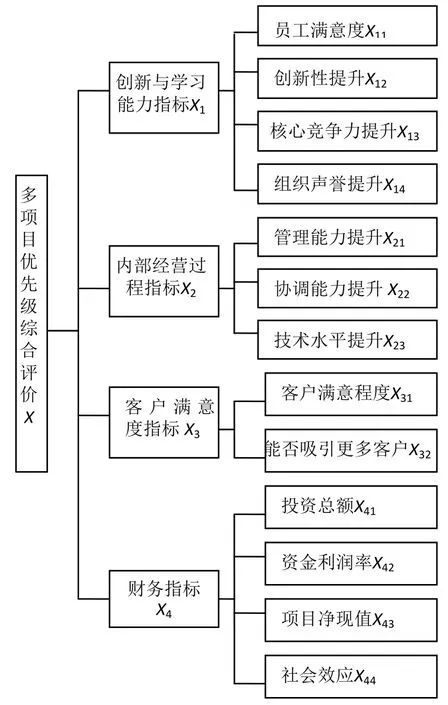
图1 多项目优先级评价系统
1.3确定评价指标系统权值
项目优先级评价的重中之重就是如何确定评价指标系统权值,权值的科学性和精确度将直接影响最终评价结果。现有的权值确定方法有德尔菲法、主成分分析法、层次分析法和主观赋权法等。德尔菲法不受指标是否是数据的约束,缺点是应用过程较繁,严重受专家经验、知识等因素限制,适合一些不容易量化的模糊指标。主成分分析法是采用较少的新指标来替代原来较多的指标,但是新指标不可能完全包含原指标的所有信息,存在小幅偏差,客观性较强,适合数据样本。主观赋权法虽然存在客观的基础,但是主观性还是较强。层次分析法依据内在逻辑用评价指标构成层次关系,然后对同一层进行比较,并依据约定的权值建立判断矩阵,求出判断矩阵的特征向量,然后将该向量归一化,最终得到各指标的权值。该方法可信度大,更具逻辑性,且应用范围较广。缺点是指标间重要度的判断因人而异,具有一定的主观性,适用于样本数据指标或模糊性指标。本文主要采用层次分析法。
首先通过FAHP法确定第一层各指标的相应权值A=(a1,a2,…,aM),其中a1+a2+…+aM=1,其次,第二层指各标相应权值Ai=(ai1,ai2,…,aiU),同样ai1+ai2+…+aiU=1。i表示第一层指标代码。M,U分别为第一层和第二层指标集的长度,如果有第三层和第四层可以此类推。
1.4确定评价指标系统的评语集
本文中W=(W1,W2,W3,W4,W5),分别代表优,良,可,差,很差。其中,W1可以用数字化为1,W2可以用数字化为0.8,以此类推,W3为0.6,W4为0.4,W5为0.2。
1.5确定评价指标系统的评价矩阵Ri
评价过程中可以选择N位专家,对二级评价指标(xi)中的各项指标(xij)进行评价,依据评语分布及评价人员总数可确定如式(1)所示的评价矩阵Ri。

式(1)中rjm表示二级指标(xij)评语(Wm)的隶属度。评价矩阵的值确定方法如下:N个专家对xij共有N个Wk的评分结果,则rjm的值是xij中相同的评语的数量除N,二级指标集的长度表示为U。
1.6评价指标系统的模糊矩阵运算
对二级指标(Xij)的评价矩阵(Ri)进行模糊矩阵运算,可获得一级指标(Xi)对评语集(W)的隶属向量(B)。

因此,一级指标(A)的各隶属向量可形成一个评价矩阵(B),再对评价矩阵(B)进行矩阵运算,即可得到向量C。

1.7评价指标系统的评价结果
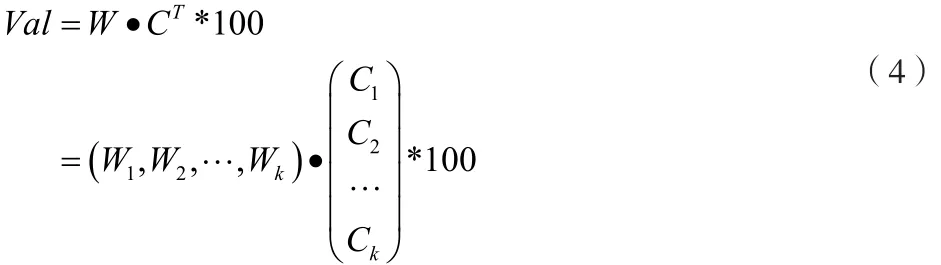
由式(4)可知项目优先级的评价结果。依据最终的Val值,就可以排列出多项目的优先级。
2 实例分析
以一家大型国企为例,该企业专业齐全,技术实力雄厚。现该企业承担了3个工程项目的施工工作。相对于所承接项目的规模和数量而言,企业的设备、人力等资源相对紧缺。为提高各方面的资源利用率,需要合理地在3个项目间分配资源,以尽可能确保交付进度和工程质量。现对该企业的3个项目,依据上述4个指标,采用模糊层次分析法对优先级来进行评价。
首先需获取3个项目的信息,然后采用层次分析法和专家咨询法来确定各指标权值。各专家首先评估各指标的重要性,然后构造判断矩阵,求出该矩阵的特征值和特征向量,得出各指标权值。该实例中各级指标权值见图2。

图2 评价指标的权值示意图
在确定指标权值之后,就要确定评语集W=(优,良,可,差,很差),对应数值分别为5,4,3,2,1,选择5位专家对上述3个项目的诸指标进行评分。专家评分结果见表1,表2,表3。
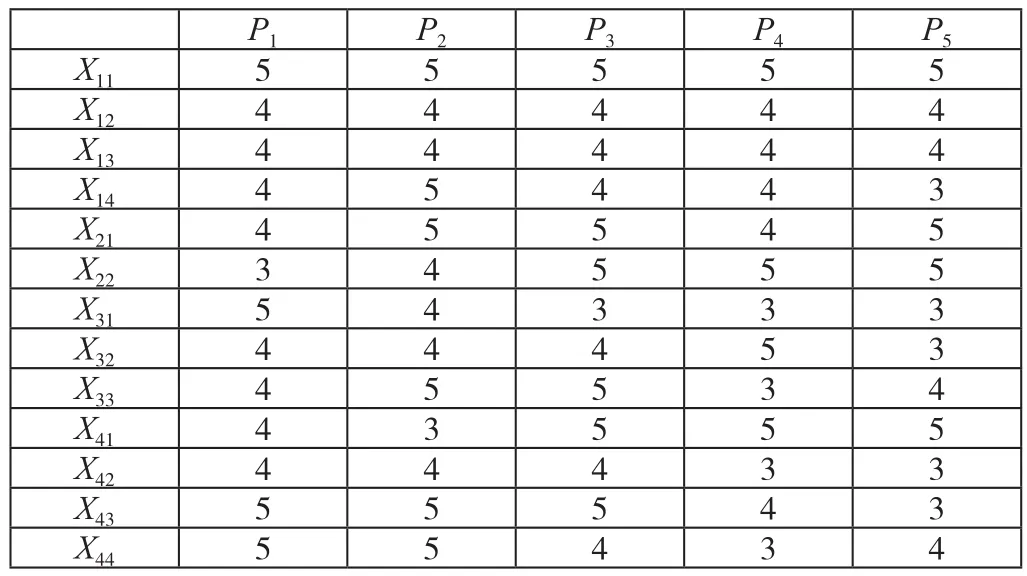
表1 第1个项目的专家评分表

表2 第2个项目的专家评分表

表3 第3个项目的专家评分表
以第一个项目为例,来说明基于模糊层次分析法的评价方法的应用。该项目的模糊评价矩阵如下:

且:A1=(0.31,0.26,0.15,0.28);A2=(0.65,0.35);A3=(0.39,0.19,0.42);A4=(0.15,0.12,0.38,0.35)。A1表示下层权重。由上可得:
B1=A1·R1=(0.366,0.578,0.056,0,0);
B2=A2·R2=(0.6,0.33,0.07,0,0);
B3=A3·R3=(0.362,0.36,0.278,0,0);
B4=A4·R4=(0.458,0.318,0.224,0,0);
至此,专家组分别对该项目的创新与成长、内部经营、客户满意度和财务指标4个方面给出了评价。
接下来,对该项目给出最终评价:

同理,可以得出第二、第三个项目的模糊评价。
C2=(0,0.357 6,0.532 3,0.112 4,0)
C3=(0,0.211 7,0.473 6,0.277 8,0.037)
取评价标准的评语集为:W={1(优),0.8(良),0.6(可),0.4(差),0.2(很差)}
则第一个项目的优先级评价分数为:

同理,第二个和第三个项目的分数分别为:65.04和57.2。
以上实例运用模糊层次分析法评价3个项目的优先级,体现了上述项目的重要程度,也反映出上述项目在有限资源约束下的优先级。
3 结 语
优先级冲突是多项目管理中最重要的冲突之一。解决该冲突是企业制定多项目计划和进行资源配置的前提条件。本文在项目优先级评定中采用了模糊层次分析法,为多项目管理中如何评定项目优先级提供了一种新的方法和思路。实例表明,利用模糊层次分析法确定项目优先级计算结果较为稳定、客观,简便实用,具有较强的适用性。
注:王锐鑫,通讯作者
主要参考文献
[1]郭燕,梁工谦.一种判断企业内部项目优先级的定量评价方法[J].航空制造技术,2006(5):98-102.
[2]谭云涛,郭波,郑敏.企业多项目管理中的优先排序问题研究[J].管理工程学报,2005(z1):152-155.
[3]樊为刚,侯丽红.层次分析法的改进[J].科技情报开发与经济,2005,14(4):153-154.
[4]李永.多目标决策中目标权重的确定法[J].甘肃工业大学学报,2003,29(3):118-119.
[5][美]Saaty T L.层次分析法[M].许树柏,译.北京:煤炭工业出版社,1988.
[6]万阳,王立海.基于模糊层次分析法的采购质量方案优选[J].森林工程,2006,22(1):3-5.
10.3969/j.issn.1673 - 0194.2015.12.051
F062.4
A
1673-0194(2015)12-0066-03
2015-04-22
国家863项目(2011AA110101)。
