基于小波变换的多聚焦图像融合算法研究

2015-09-18赵慧

产业与科技论坛 2015年22期

赵慧

一、引言

一般情况下，成像系统无法对同一场景中不同距离的物体都形成清晰的像，因此图像融合应运而生。图像融合是将同一场景内的多幅图像融合成一幅各处都清晰的图像的过程。融合后的图像能更好地适合人的视觉感知、满足计算机处理的需求，而且能使图像信息更全面地表现出来，进而提高图像分辨率，使图像更加清晰[1]。近年来已成功应用于目标识别与跟踪、机器视觉以及医学诊断等方面[2]。多聚焦图像融合是图像融合的一个典型的研究领域。

多聚焦图像融合的方法可以分为两大类，分别是基于空域的多聚焦图像融合方法和基于变换域的多聚焦图像融合方法。本文主要研究基于小波变换的多聚焦图像融合方法，从小波变换的高频域和低频域两个角度讨论了几种典型的多聚焦图像融合方法，选择不同的小波基函数对融合结果的影响也不相同。

二、多聚焦图像的融合原理

由光学的成像系统理论可以得知，只有在物体齐焦(即物体处于物镜的聚焦平面)状态下，才能得到最清晰的成像，而当物体离开聚焦平面成像时，就会出现一定的模糊现象，所以成像模糊的程度与物体的位置是有直接关系的。通过调整镜头的位置来采集聚焦在物体不同点位的图像序列。整个图像序列包含物体在镜头中全部信息，每幅图像都有聚焦清晰和聚焦模糊的区域，所以在图像序列中获得每个像素聚焦清晰的位置，通过一定的融合规则就能重建一幅清晰的图像[3]。

三、小波变换分解的基本原理

小波变换是在空间(时间)上和频率上的局部变换，是进行信号时频分析和处理的理想工具。它是通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

二维小波变换通过利用两个一维的滤波器对二维的图像进行快速的小波分解，然后进行图像重构，实现图像的融合。用C0表示原始图像f(x，y)，两个一维的镜像滤波算子设为H和G，分别用来表示低通和高通，依据Mallat的小波算法，尺度为j的分解公式如下:

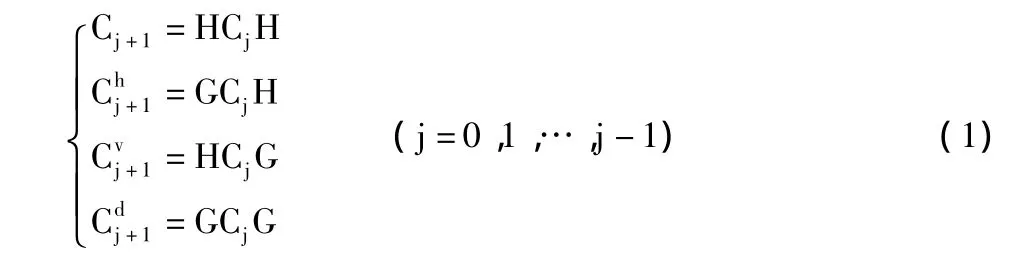
此时，水平、垂直、对角方向的高频分量分别用h、v、d来表示;H与G的共轭转置矩阵分别用和H来G表示，与其对应的二维图像的小波的重构算法如下:

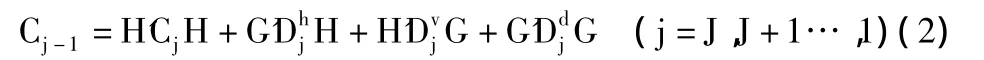
这里，J表示分解层数。

经过小波分解后，图像高频区域表示图像的细节部分，反映的是图像边缘等信息;而图像低频的区域，则反映图像的近似和平均特性。

四、基于小波变换的多聚焦融合算法

一幅图像采取小波变换算法之后，绝对值比较大的小波系数与具有显著变化特征的边缘相对应，小波融合的低频系数能够决定图像序列的轮廓部分(图像变化平缓部分)。

对于源图像运用层的小波分解，对其水平、垂直和对角方向的分量分别处理，将每幅图像高频系数在各尺度j(j=1～J)上分别对比，小波系数绝对值较大的分量对应图像灰度值变化较大的边缘部分的特征，人眼对于此类特征较敏感。因此，可以将对应位置上绝对值比较大的系数作为融合后图像序列在小波域中的高频系数[4]。

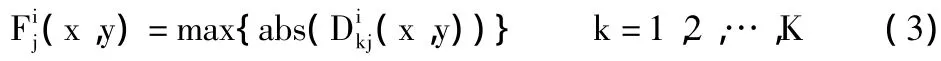
此时，多聚焦图像序列数目用来K表示;i=1，2，3表示小波分解的系数(分别表示水平、垂直、对角三个方向的);第k幅图像序列在点(x，y)处第j层的小波分解系数用来表示;abs表示对小波分解系数(x，y)的绝对值;对第个小波分解系数的最大值用max{abs((x，y))}来表示(x，y)表示融合的图像序列在(x，y)处第j层的小波分解系数。

对于同一序列的多聚焦图像，它低频区域对应的数值是相同或者相近的，但是高频区域的子图像区别很大，所以说低频系数在图像序列中的平均值可以确定融合图像的低频分量，这种方法是基于小波变换的多聚焦图像融合方法中常用的方法[5]。

若多聚焦图像序列的数目用K表示，第k幅图像序列在(x，y)处的第 j层小波分解低频系数用 Ck，j(x，y)表示;第 j层的融合后的图像序列的低频系数用Cj表示，则:

通过小波变换的方法处理多聚焦图像融合的过程中，小波基函数不是唯一的，采用不同的小波基函数会产生不同的融合效果。所以在进行图像融合时不仅要选择适合的高频、低频的融合算子，还要挑选出合适的小波基函数。常用的小波基函数有Haar小波、Daubechies小波(记为 dbN，N表示序号，下同)、Biorthogonal小波(bioNr.Nd)、Coiflet小波(CoifN)、Symlets小波(symN)。

五、多聚焦融合图像的结果分析

评价多聚焦融合图像的方法有主观和客观两类评定法[6]。主观评定是观察者根据规定的评价尺度、个人经验或参照标准图像用目测法对融合图像进行评定。而客观评定法是利用一些量化的评价参数对融合图像的质量进行判断，可以提高判断的速度和准确性。常用的客观评价参数有信息熵、图像均值以及标准差。

对于图像I，设为图像函数I(x，y)，M和N分别表示图像的行数、列数。

(一)信息熵。熵指数用来衡量图像信息的丰富程度，其大小反映了图像中包含信息量的多少。如果把一幅图像的各个像素都看成独立样本，则图像灰度值的分布可表示成p={p0，p1，…，pi，…，pL－1}，pi表示灰度值是i的像素数和总像素数之比，L表示总的灰度级。根据香农理论，图像的信息熵可表示为:

图像的信息熵越大，表示融合后的图像所含的信息越丰富，融合后图像的效果也就越好。

(二)均值[8]。即图像灰度的平均值，对于人眼则反映为平均亮度，若均值适中，则视觉效果良好。图像的均值表示为:

(三)标准差[9]。图像的标准差用来表示图像灰度对灰度平均值离散的情况，在某种情况下可用来反映图像反差的大小。图像的标准差越小，图像反差越小，对比度越小，无法看出太多的信息，而图像的标准差越大，图像反差越大，对比度越大，可以得到的信息就更多。图像的标准差表示为:

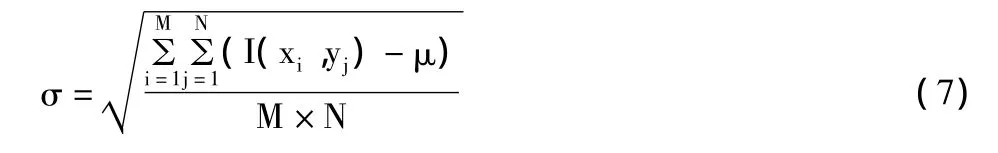
其中μ为图像灰度的均值。

对于目标图像的三个参数值分别为E=7.0097、μ=118.7245、σ =62.3417。

本文对小波变换的多聚焦图像融合方法进行研究，采用高频系数绝对值最大法处理多聚焦图像的高频部分和低频系数平均法处理多聚焦图像的低频部分，最后将处理后的图像进行重构。图1是多聚焦的序列图像，对其采用小波变换融合后的图像图2所示。

图1 聚焦清晰的区域不同的序列图像

表1 采用小波变换融合方法对图1处理结果的性能评价

采用三个评价参数对五种采用不同小波基函数融合后的图像客观评价如表1所示。将表1的数据与目标图像的对应参数相比较，可以得出采用Haar小波基函数、sym3小波基函数和bior1.3小波基函数获得的融合图像的信息熵和标准差都偏小，不能获得比较多的图像信息;coif3小波基函数和db9小波基函数处理后的图像目标图像参数的差距最小。