一种基于分段式字符集的彩虹表明文生成方式∗

张琛岭

(上海交通大学电子信息与电气工程学院，上海200240)

一种基于分段式字符集的彩虹表明文生成方式∗

张琛岭

(上海交通大学电子信息与电气工程学院，上海200240)

Oechslin提出的彩虹表应用时间空间折中思想,是密码学中逆转单向函数的有效工具,但现在广泛使用的单一字符集彩虹表,在明文位数较大时,因明文空间的迅速膨胀,消耗计算资源的迅速增加,其应用遇到了瓶颈。为此,针对人为口令字符集构成特点,提出分段式字符集彩虹表明文生成方式,将取自不同字符集的不同位数明文拼接组成新的明文,可以有效地压缩明文空间,增加覆盖的最大明文位数。对取自CSDN的1000个真实口令哈希进行实验,结果表明,在原始彩虹表的基础上,使用分段式字符集彩虹表使恢复成功率提升39.1%。

单向函数;时间空间折中;彩虹表;真实口令;分段式字符集;哈希恢复成功率

0 引言

单向函数的逆转问题是密码学中一个重要的研究方向,当所针对的明文空间较大时,单纯的时间暴力破解或查表破解往往无法满足要求。1980年Hellman首次提出时间空间折中算法(TMTO)[1],以部分存储空间为代价,缩减在线破解时间,并将其应用于DES的破解。之后Rivest提出可区分点算法(DP)[2],仍以时间空间折中思想为基础,对Hellman的算法进行了一些改动,使得所需查表次数明显减少。彩虹表算法是Oechslin于2003年提出的基于时间空间折中思想的算法[3],它的预计算表在结构上与前两种算法均不相同,表的数量很少,但每张表中使用了多个R函数,且链长保持一致。Oechslin将其应用于PC上Windows口令的破解,并取得了很好的效果。

彩虹表算法在其被提出后的十多年中得到了很好的发展,在理论上,文献[4]对完美的经典Hellman表、DP表[5]以及彩虹表[3]进行了分析,并使用一种基于检查点(checkpoint)的新技术[6],通过概率性地排除误警来进一步减小破解时间;Thing和Ying等通过改进初始链生成方式[7]、排序方法[8]和增加针对字典口令的恢复方式[9]等来进一步优化彩虹表;Jin Hong等对彩虹表等时间空间折中算法做了大量计算工作,包括对误警的分析[10]、对非完美模糊彩虹表的分析[11]以及对多种时间空间折中算法的分析和比较[12,13]。而在工程上,也有很多项目或个人对彩虹表进行研究和使用。

近年,GPU运算能力发展迅速,GPGPU广泛用于密码学领域,也包括单向函数的运算,并出现了应用于彩虹表的研究[14]和项目。GPU带来的运算性能的提升使得生成针对更大明文空间的彩虹表更为容易,扩大了彩虹表的使用范围,而另一方面,当进行人为口令哈希恢复时,我们通过改变明文的生成方式,压缩长口令明文空间,可以进一步提升彩虹表的明文恢复成功率。

1 分段式字符集彩虹表

1.1 提出

原始的Oechslin彩虹表仅针对单一字符集覆盖不同长度明文,如选自大小写字母、数字以及特殊符号构成的字符集的1至8位的明文,其明文空间大小为6161234432565770,即6.16×1015,若生成一张破解成功率约57%左右的彩虹表,以每秒5×108明文的GPU生成速度为例,需要约148天,虽然可以覆盖全部1至8位的由大小写字母、数字以及特殊符号构成的明文,但所需计算资源量很大,且覆盖最长明文位数仅为8位。

本文提出一种新的分段式字符集明文生成方式,将原始彩虹表的单一字符集明文生成方式扩展为多字符集构成的分段式明文拼接生成方式,剔除掉人为口令中不常见的随机字符明文(如取自由大小写字母、数字以及特殊符号构成的字符集的8位明文“＠o:＝Ks＾o”),有针对性地生成出现概率更高的明文(如同样是取自由大小写字母、数字以及特殊符号构成的字符集的8位明文“Love＠250”),以缩减明文空间。

分段式字符集明文拼接生成方式,是将多段可变长度的由不同字符集的字符构成的明文拼接为最终明文的生成方式。如由1位大写字母、1至3位小写字母、1位特殊符号以及1至3位数字构成的分段式字符集,可以覆盖形如“Love＠250”、“Good＆520”、“Abc:123”、“Bug∗99”等 8 位及 8 位以内明文,而其明文空间大小只有16880098560,即1.69×1010,若生成一张破解成功率约57%左右的彩虹表,同样以每秒5×108明文的GPU生成速度为例,只需约36秒。

1.2 彩虹链生成流程

彩虹表有若干彩虹链组成,彩虹链由若干彩虹表节点构成,各彩虹表节点由与明文一一对应的序号表示,每一个节点经过“序号转明文”、“明文转哈希”、“哈希转序号”等三步生成同一条彩虹链的下一个节点(如图1所示)。其中“明文转哈希”用H表示,即对一个明文字符串进行哈希运算;“哈希转序号”和“序号转明文”共同构成还原函数,用R表示,其中“哈希转序号”截取哈希前64比特,加上当前节点在彩虹链的位置序号,再加上彩虹表序号与65536的乘积,最后模明文空间大小,得到节点序号;而“序号转明文”的过程决定了明文的构成方式,包括原始彩虹表明文生成方式和分段式字符集明文生成方式;还原函数R和哈希函数H共同构成彩虹链的生成函数F＝R°H。

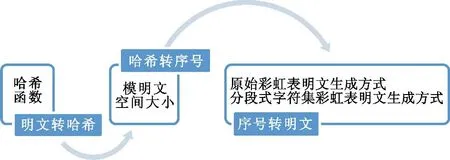
图1 彩虹链生成流程

1.2.1 原始彩虹表明文生成方式

原始彩虹表的明文生成方式主要包括计算明文长度和生成明文两个部分,过程如下:

0)准备过程:计算明文空间大小和不同长度明文对应最大序号。

准备过程只在生成彩虹表之前进行一次,不属于明文生成过程。

1)计算明文长度

a)初始化明文长度为最大长度。

b)判断序号是否属于该长度所对应的序号范围,如果是,确定明文长度,过程结束。

c)长度减少1,然后重复进行上一步b),直到确定明文长度。

2)生成明文

a)序号减去与所得长度减1对应的最大序号,更新为新的序号。

b)序号模字符集长度,根据结果找到字符集中对应的字符,拼接至明文。

c)序号除以字符集长度,然后重复上一步b),直到达到明文长度。

1.2.2 分段式彩虹表明文生成方式

分段式字符集明文拼接生成方式,在原始彩虹表的明文生成方式基础之上进行了扩展,将多段取自不同字符集的明文进行拼接(允许多个分段的字符集相同,但相邻字符集若相同则没有意义,反而会带来性能下降,应该合并为一个字符集),形成新的明文,总的明文空间大小是各段明文的明文空间大小之积。在开始生成彩虹链之前计算总的明文空间大小和各分段明文空间大小。明文生成过程如下:

1)序号模一段明文空间大小,结果作为原始彩虹表明文生成方式的输入序号,进行原始彩虹表明文生成过程,获得该段明文。

2)序号除该段明文空间大小,然后按序选择下一段明文,重复上一步1),直到生成所有分段的明文。

3)将生成的各段明文按序拼接为最终明文。

1.3 明文空间计算

原始彩虹表只有一段字符集,分别用L、Min和Max表示其字符集大小、最小明文长度和最大明文长度,则其明文空间大小为

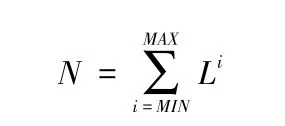
分段式字符集彩虹表包括一至多段字符集,分别用Li、Mini和Maxi表示各字符集大小、与各字符集对应的最小明文长度和最大明文长度,用n表示段数。

分段式字符集彩虹表明文空间大小为

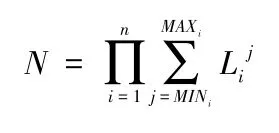
2 CSDN真实口令处理能力分析

本文对CSDN真实口令数据进行明文字符集组成的分析,得到如下结果。

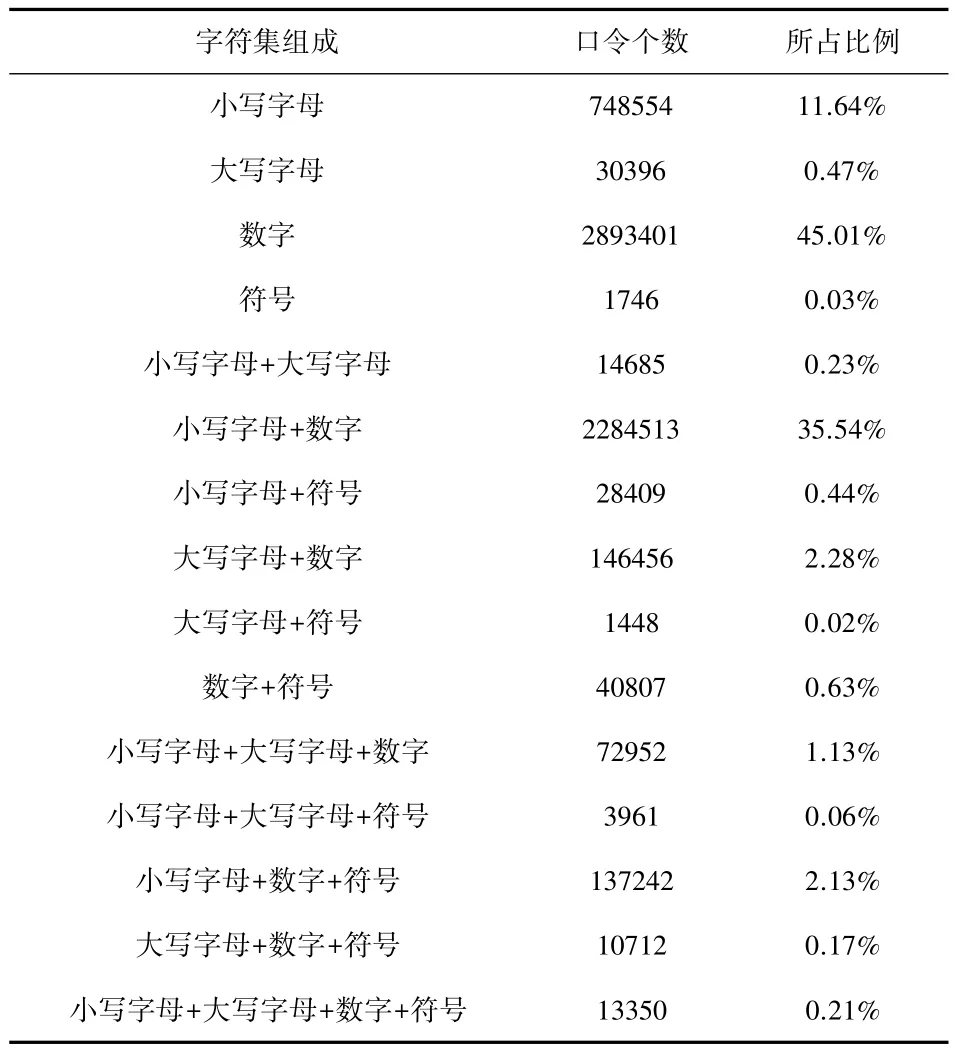
表1 CSDN真实口令字符集组成统计信息

以真实口令作为数据,我们分析分段式字符集彩虹表对不同字符集组合的明文处理能力。以比例较大的“小写字母和数字”字符集组合方式的明文为数据,分析分段式字符集彩虹表对明文空间的压缩情况。将字符集组合方式分为三类:若干位小写字母连接若干位数字、若干位数字连接若干位小写字母、其他。经过对口令的统计分析,三类口令数量依次为:1680061、378252、226200。明文长度主要分布在15位以内(98.4%),最长的为19位。1至15位取自由小写字母和数字构成的字符集的明文,其明文空间大小为227390317427040025268340,即2.27×1023,这是一个巨大的数字,以至现有的计算资源几乎无法针对该位数范围的单一字符集生成一张有效的彩虹表(事实上,原始彩虹表在处理11位明文时,已显得捉襟见肘)。于是我们可以采用分段式字符集构成方式缩减明文空间,以扩大明文覆盖范围。

下面分别计算原始彩虹表(表2)和分段式字符集彩虹表(表3)对CSDN用户口令中小写字母和数字组成的明文的处理能力,并进行对比分析,其中以3×106节点/秒和5×108节点/秒分别作为CPU和GPU生成彩虹表的估计速率。

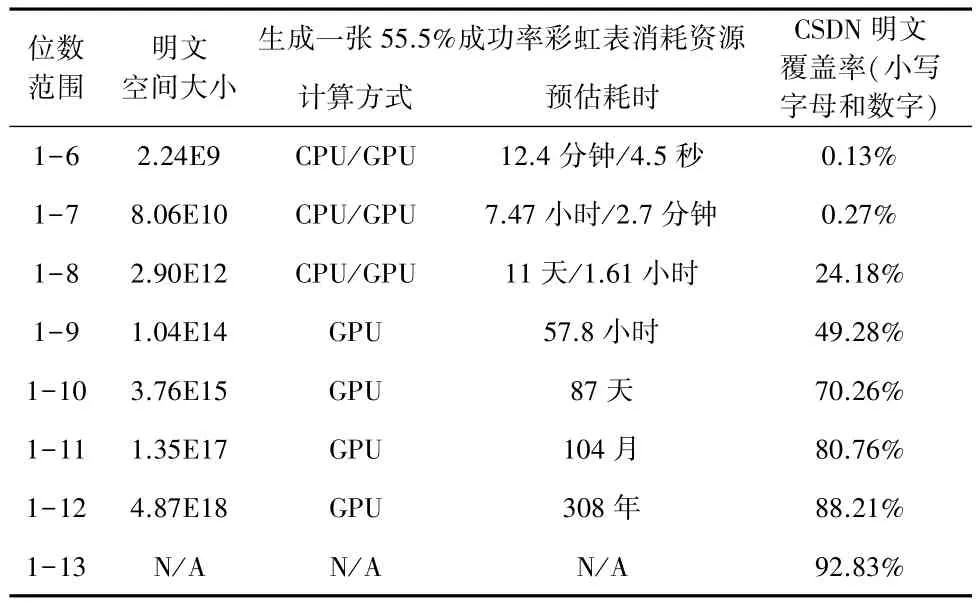
表2 原始彩虹表口令处理能力

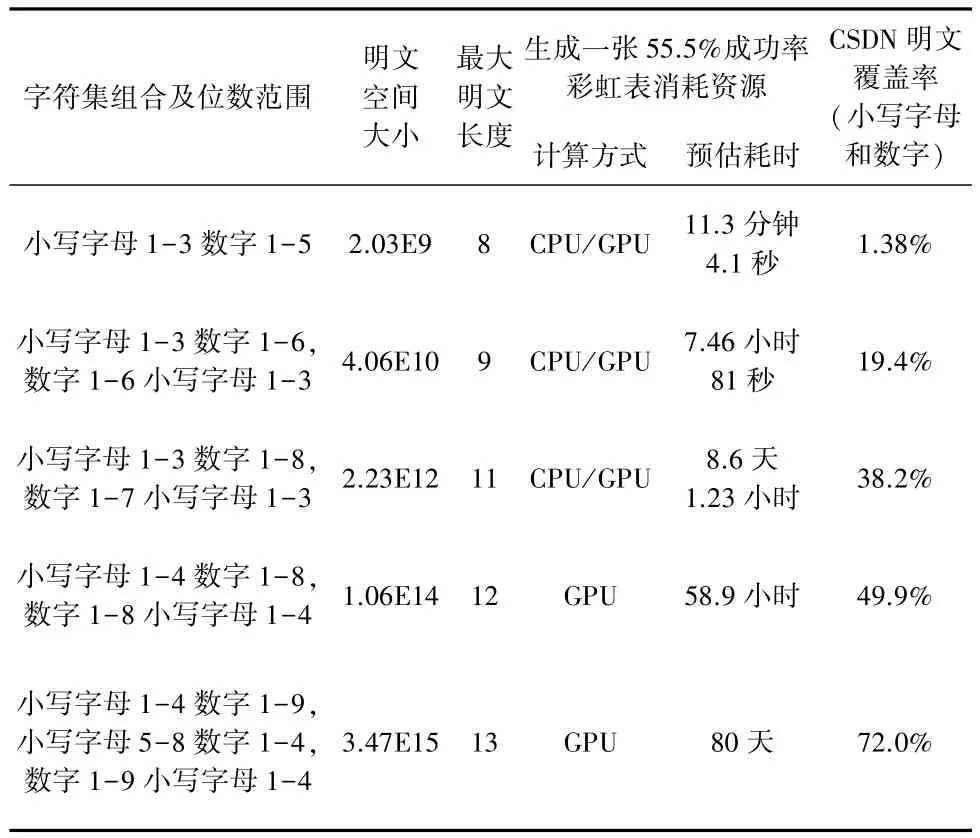
表3 分段式字符集彩虹表口令处理能力

观察可知,在较小明文空间大小的情况下(小于1013),分段式字符集彩虹表可以通过选择明文覆盖率更高的字符集和位数组合的方式,以更小的明文空间大小(更少的彩虹表计算资源消耗),达到更高的命中率(0.13%提高至1.38%,0.27%提高至19.4%,24.18%提高至38.2%);在较大明文空间大小的情况下,分段式字符集彩虹表在消耗的计算资源和命中率方面都不比原始彩虹表差,甚至表现更好,而且更为重要的是,前者可以覆盖到的明文长度范围更广(平均提高了3位),而后者在处理10位以上明文时,则很难生成有效的彩虹表;另外,我们注意到,随着明文空间大小的增加,无论是原始彩虹表还是分段式字符集彩虹表,生成相应有效彩虹表所需的计算资源很快超出可接受范围,而且命中率增长缓慢,很快达到极限,这时如果将两者结合使用,则可以有效提高命中率,以1015数量级的明文空间大小达到近80%命中率。

3 实验与结果分析

针对常见的小写字母和数字字符集,我们分别生成原始彩虹表和分段式字符集彩虹表,详细信息如下表所示。

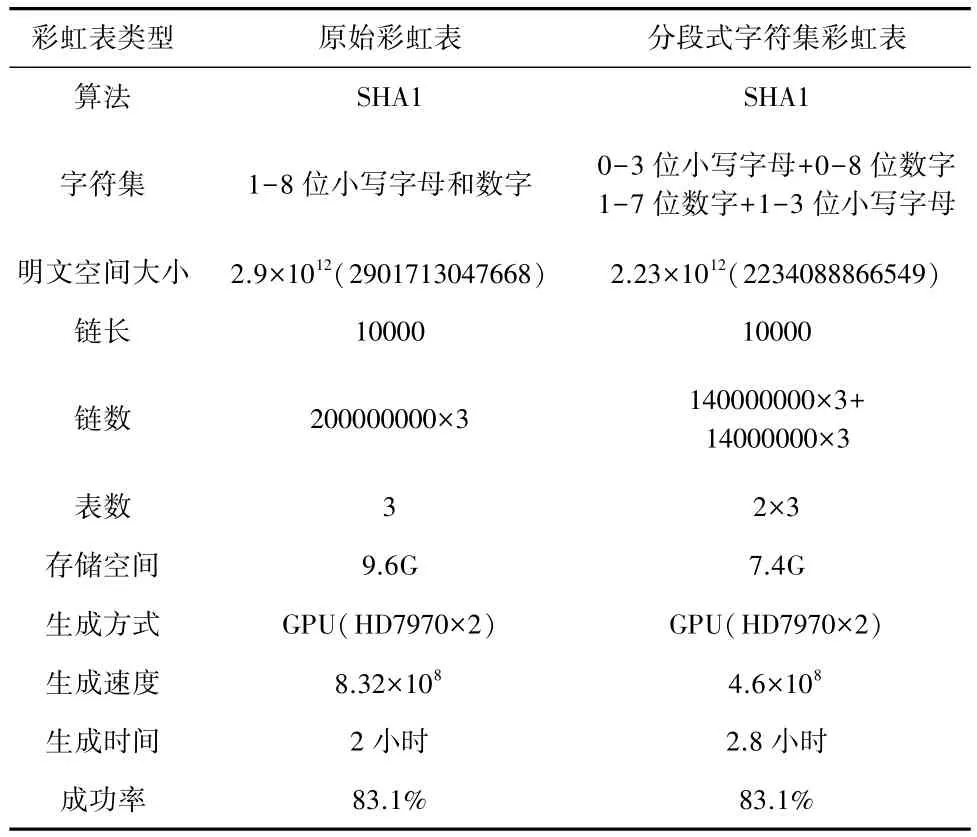
表4 实验信息

从6428632个CSDN口令中随机挑选1,000个生成SHA1哈希,然后使用以上彩虹表对其进行恢复,获得如下结果。

表5 实验结果

由统计数据可知,原始彩虹表与分段式字符集彩虹表相结合,可以使哈希恢复成功率由30.4%提升至42.3%,恢复效果提升39.1%。结果表明,分段式字符集彩虹表针对人为口令特点,可以对明文空间进行有效压缩,扩展明文的覆盖范围,提高恢复成功率。

4 结语

针对原始彩虹表处理较大位数明文能力不足的问题,本文结合人为口令字符集构成特点,提出一种分段式字符集彩虹表明文生成方式,将取自不同字符集的明文拼接为新的明文,以扩展可以覆盖的明文位数。以CSDN真实口令数据为基础,对分段式字符集彩虹表的应用进行了分析与实验,结果表明,分段式字符集彩虹表可以有效压缩明文空间,在原始彩虹表的基础上明显提高口令哈希恢复成功率。因新的明文生成方式较原始彩虹表复杂,R函数在GPU上的执行速度有明显下降,下一步的工作是继续优化R函数在GPU上的执行过程,以提升彩虹链生成速度。

[1] Hellman M E.A cryptanalytic time－memory trade－off[J].Information Theory:IEEE Transactions on,1980,26(4):401－406.

[2] Robling Denning D E.Cryptography and data security[M].Addison－Wesley Longman Publishing Co.Inc..USA:Addison－Wesley,1982:100.

[3] Oechslin P.Making a faster cryptanalytic time－memory tradeoff[M].Advances in Cryptology－CRYPTO.Berlin:Springer Berlin Heidelberg,2003:617－630.

[5] Borst J,Preneel B,Vandewalle J.On the time－memory tradeoff between exhaustive key search and table precomputation[C]//Symposium on Information Theory in the Benelux.Veldhoven(NL):TECHNISCHE UNIVERSITEIT DELFT,1998:111－118.

[6] Avoine G,Junod P,Oechslin P.Time－memory trade－offs:False alarm detection using checkpoints[M].Progress in Cryptology－INDOCRYPT.2005.Berlin:Springer Berlin Heidelberg,2005:183－196.

[8] Ying H M,Thing V LL.A novel rainbow table sorting method[C]//The Second International Conference on Technical and Legal Aspects of the e－Society.Gosier,Guadeloupe,France:CYBERLAWS,2011:35－40.

[9] Thing V LL,Ying H M.Enhanced Dictionary Based Rainbow Table[M]//Information Security and Privacy Research.Berlin:Springer Berlin Heidelberg,2012:513－524.

[11] Kim B I,Hong J.Analysis of the non－perfect table fuzzy rainbow tradeoff[C]//Information Security and Privacy.Berlin:Springer Berlin Heidelberg,2013:347－362.

[13] Lee G W,Hong J.A Comparison of Perfect Table Cryptanalytic TradeoffAlgorithms[J].IACR Cryptology ePrint Archive,2012:540－540.

[14] Kim JW,Seo J,Hong J,Park K,Kim SR.High－speed parallel implementations of the rainbow method in a heterogeneous system[J].INDOCRYPT,2012:303–316.

A Rainbow－Table Plain Generation Method based on Segmented Charset

ZHANG Chen－ling
(School of Electronic Information and Electrical Engineering,SJTU,Shanghai 200240,China)

TMTO(Time Memory Trade Off)－based rainbow table method,proposed by Oechslin,is a useful one－way function reversing method in cryptography.However,the world widely used original rainbow table method,which uses a single charset,could not be applied efficiently when dealing with a long plain due to the lack of computing resource and the significant increase of plain space.In considering the character of human passwords constitution,a new plain generation method based on segmented charset is introduced,which splices the plains from different charsets and forms a new plain.This method could effectively reduce the plain space and increase the max plain length the rainbow table is able to cover.The experiment recovering 1000 hashes corresponding to plains taken from the revealed CSDN password library indicates that the rainbow－table plain generation method based on segmented charset could raise the success rate of hash recovering by 39.1%when used in combination of the original rainbow table method.

one－way function,time－memory tradeoff,rainbow table,human password,segmented charset,success rate of hash recovering

TP309－7

A

1009－8054(2015)01－0099－04

2014－08－25

上海市科委计划项目(No.13JG0500400)

张琛岭(1990—),男,硕士研究生,主要研究方向为密码学。■