基于LBP-DEELM的木材纹理分类算法

向 东，陈 宇，陈广胜

(东北林业大学信息与计算机工程学院，黑龙江 哈尔滨 150040)

基于LBP-DEELM的木材纹理分类算法

向 东，陈 宇，陈广胜

(东北林业大学信息与计算机工程学院，黑龙江 哈尔滨 150040)

为解决传统木材纹理分类的准确率低且难度大的问题，提出了一种基于LBP-DEELM(局部二值-差分演化优化极限学习机)模型的木材纹理分类算法。在阐述局部二值算子(LBP)和差分演化优化极限学习机(DEELM)算法的基础上，使用均匀旋转不变的LBP模式提取纹理的特征值，结合差分演化算法进行极限学习机优化，通过训练得到每类纹理所对应的分类器模型参数，构造分类器，实现了对木材纹理准确高效的分类。实验结果表明，相比于BP神经网络，SVM支持向量机等分类算法，该模型的实验误差率为2%左右，准确率高，实用性强。

木材纹理分类；LBP算子；差分演化优化极限学习机；分类器

木材纹理分类[1]是木材优化利用的重要部分，但限于木材纹理的天然属性，纹理结构精细复杂、无规律，使得纹理分类一直是木材学的前沿课题。近年来随着计算机视觉技术的发展，将其引入木材学，也为解决木材纹理分类问题提供了新思路。针对不同的分类研究，国内外学者提出了不同的特征提取及纹理分类的算法，灰度共生矩阵法，马尔可夫随机场，尺度不变特征变换法等在特征提取方面取得了一定的突破；而常用的分类算法有BP神经网络、SVM支持向量机[2]、决策树[3]、贝叶斯、Gauss-Newton(高斯牛顿)等。然而我国对于木材纹理分类的研究起步较晚，初期主要是对国外的经验总结，优化传统的分类算法，大多纹理分类模型都是基于以上算法的结合，取得了一定的成果；但仍存在一定缺陷，主要是实际应用的训练样本在个体之间存在差异，导致分类算法对分类结果的差异性较大，因此本文研究的重点就是如何有效提高木材纹理分类的准确性。

针对于木材纹理特征的提取，一种简单高效的纹理特征分析方法——LBP(局部二值模式，最早是由Ojala等在1996年提出)成为了众多学者研究的对象，在描述、提取局部纹理特征方面取得了较好的效果。此外，极限学习机[4](Extreme Learning Machine，ELM)是一种前馈式的神经网络算法，最早由南洋理工大学G.B.Huang等人在2004年提出，通过输入权值和隐含层的随机赋值，最终得到目标值。ELM因其快速的训练速度在单隐层前馈网络应用中应用广泛，根据随机隐层节点参数，利用最小二乘法计算输出权值，这些特征使得极限学习机克服了一些存在于传统的梯度下降算法的限制，例如局部极小，收敛速度慢。但是在ELM中，隐层节点数是优先分配的，隐层参数是随机选择且在整个训练过程中保持不变，因此一些非最优节点可以存在，但在最优化的成本函数中贡献较少，况且连接权值和阈值的选取将直接影响算法的稳定性。适逢差分演化(Differential Evolutation，DE)算法[5]是一类基于种群的启发式全局搜索技术，对于参数的优化具有很强的鲁棒性。鉴于以上表述，利用差分演化算法优化网络的输入参数，ELM根据输入参数最终计算输出权值，因此，提出一种应用于单隐层前馈网络的算法DEELM(差分演化优化极限学习机)，DEELM不仅保证更紧凑的网络规模，而且还具有良好的泛化能力，且在木材纹理分类方面应用极少。通过LBP提取的木材纹理特征输入到DEELM分类器进行分类描述，经实验：该算法达到预期效果，并且正确率明显高于BP神经网络、SVM支持向量机。

1 木材纹理特征提取

LBP=0×128+0×64+0×32+1×16+1×8+1×4+1×2+0×1=30 图1 原始的LBP算子

实验采用局部二值模式[6]提取木材纹理特征，数学定义：原始LBP算子规定在3×3的窗体内，以窗体中心像素灰度值为阈值，与相邻8个像素的灰度值比较，若周围灰度值大于阈值，则该像素点的位置被标记为1，反之为0。这样，3×3领域内的8个点可产生8 bit的无符号数，即该窗体的LBP值，并用这个值来反映该区域的纹理信息(图1)。

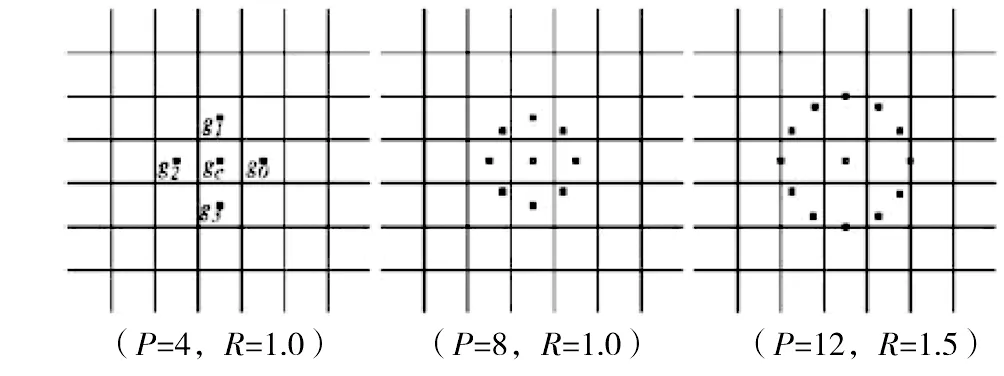
图2 不同半径、邻点的圆形区域

随着LBP算子在图像中的应用，实验设定1个半径为R(R>0)的圆形邻域，LBP值可以通过公式(1)进行计算：

(1)

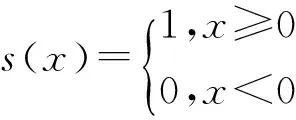
(2)

式中：gc为中心像素的灰度值；gp为周围邻点的灰度值；P为邻点个数；R为邻接半径。假定gc的坐标为(0，0)，即gp的坐标为(-Rsin(2πp/P)，Rcos(2πp/P))。图2也表明了不同半径，不同邻点个数所对应的圆形区域。

假定纹理图像是N×M的，在确定每个像素点的LBP值后，整个纹理图像可通过建立1个直方图进行表示：

(3)

(4)

实验中总是需要考虑木材纹理特征的空间转换数量的问题，即通过U值来确定：

(5)

由(5)式可知，LBP00000000模式的U值为0，0100000000的U值为2，在通常二进制表述上均匀模式伴随着有限的转换且不连续。经实验证实，只有均匀模式(U≤2)才可作为局部纹理的基本模式。

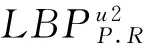
白点为1；黑点为0 图3 LBP均匀模式

(6)

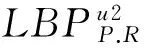
这将大大减少纹理特征矩阵的维度，所以实验采用旋转不变均匀模式下的LBP算子，且邻点个数选择8，邻接半径选择1，继而得到纹理的特征向量。实验中选取了落叶松径切，落叶松弦切提取纹理特征矩阵。结果见图4、图5。LBP算子在均匀旋转不变模式下的特征维数相对较少，同时保留了图像信息，效果最佳，最有利于实验。

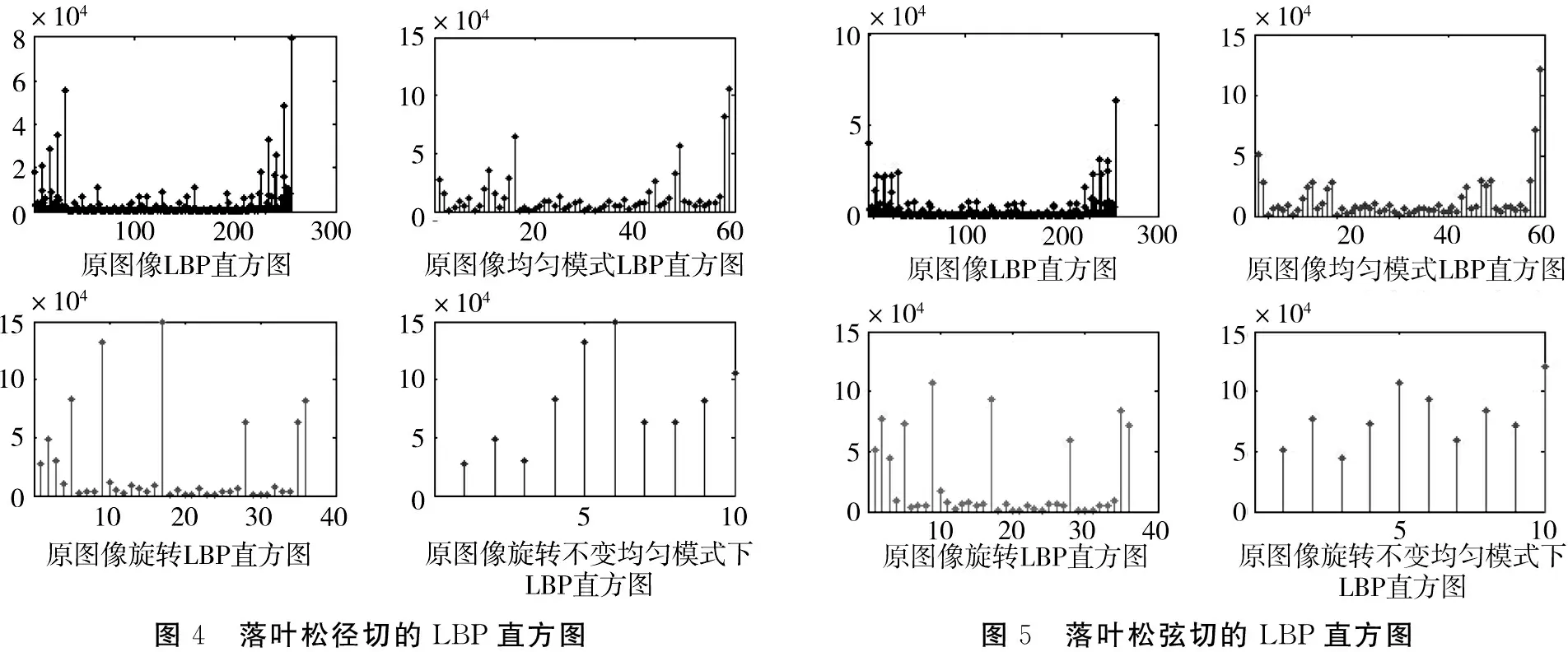
图4 落叶松径切的LBP直方图图5 落叶松弦切的LBP直方图

2 DEELM分类器的设计

2.1 差分演化算法(DE)

差分演化(Differential Evolution，DE)算法[9]是基于群体间进化的并行、直接、随机的全局搜索算法，在求解最优化的问题时，收敛速度快。核心思想源自于进化算法[10]即对当前种群进行变异，交叉操作，从而产生新的种群，择优选择种群，最终生成下一代种群[11]，实验将木材纹理特征作为种群。

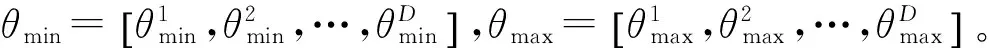
然后根据每个当代的参数向量θi，G，针对于不同问题采用不同的变异策略进行变异操作，实验利用(7)式变异策略生成1个变异向量Vi,G+1。

vi,G+1=θi,G+K×(θr1iG-θi,G)+F×(θr2i，G-θr3i，G)

(7)

(8)

式中：randj∈[0，1]；交叉概率CR∈[0，1]；随机变量jrand∈[1，2，…，D]。生成如下测试向量：

(9)

最后根据如下选择策略(10)所生成的适应函数保持为下一代种群：

(10)

实验反复执行直到目标满足或是达到最大迭代次数，差分演化过程结束。

2.2 极限学习机算法(ELM)

极限学习机[12]是一种简单有效的单隐层前馈神经网络的学习算法，设ELM算法的成本函数为：

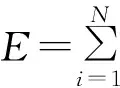
(11)

ELM算法最终为了最小化的成本函数，将采用具有激活函数的L个隐层节点的单向前馈网络使得N个纹理样本零逼近误差：

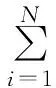
(12)

同时存在(aj，bj，βj)满足：Hβ=T，H={hi，j}是隐层的输出矩阵，并且hi，j=g(aj,bj,xi)，可得：

(13)

求出目标矩阵即为：

(14)

与此同时，ELM算法的隐层节点参数是随机分配，系统方程将会变为线性的模型，从而网络的输出权值可以通过求解最小范数的最小二乘解来表答：

(15)

式中：H+为H的MP广义逆矩阵。

2.3 DEELM分类器的设计

由于ELM算法是在训练前通过设置网络隐含层的个数，训练过程中随机选取输入连接权值和阈值，最终获取目标值，将在选取中产生非最优或不必要的输入，且对未知测试数据响应较慢，针对这个问题，本文提出用差分演化算法优化极限学习机，来达到获得最优网络目的，实现较准确的分类。同时，差分演化优化极限学习机可以完成更紧凑的网络规模，且具有更好的泛化能力，速度较快，适用于木材纹理的分类实验。差分演化优化极限学习机算法描述如下。

1)随机生成一代种群：θ=[w11,w12,…,w1k，wn1，wn2，wnk，…，b1，b2，…，bk]，wij，bj∈[-1，1]。

2)利用MP广义逆在ELM的应用计算输出权值。

3)设置成本函数验证集的适度值。成本函数为：

(16)

4)执行DE的变异，交叉，选择过程。

5)由于更小的权值泛化表现将更好，在选择过程中纳入一个标准‖β‖，将会产生新的更好的种群，表示为：

(17)

式中：f(·)为适应函数；ε为预设容忍率。

6)根据生成的下一代种群，反复执行4)～5)，直到目标满足或是达到最大迭代次数。

7)输出权值。

8)构造分类器完成，进行实验。

图6 2种木材纹理图

3 验证实验

3.1 材料与方法

实验初步选择2种木材不同切面纹理作为试材(图6)。从图6可以看出落叶松的径切、樟子松的径切近似直纹，纹路平躺均匀，结构简单；而落叶松弦切、樟子松弦切近似抛物纹，纹路曲折蜿蜒，结构复杂。实验中选取直纹样本：落叶松径切、樟子松径切训练，测试样本各50个，抛物纹样本落叶松弦切、樟子松弦切训练，测试样本各50个，总计样本数为400(表1)。

其次对样本进行预处理，采用均匀旋转不变模式LBP算子提取木材纹理特征值，初始化为特征矩阵作为训练样本，进而将初始特征矩阵加高斯白噪声形成测试初始特征矩阵，将特征矩阵作为输入种群的第G代初始向量，经过变异、交叉、选择，生成下一代种群，反复迭代满足目标，输出权值，构建分类器，对测试样本进行训练，实验流程图见图7。

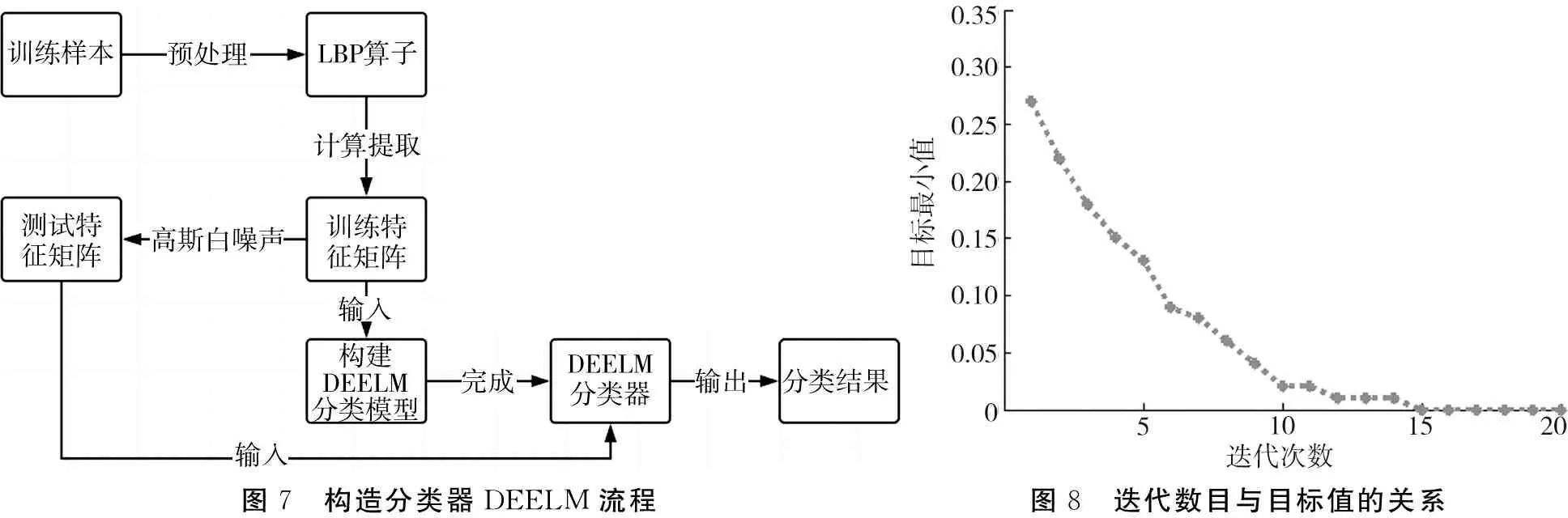
图7 构造分类器DEELM流程图8 迭代数目与目标值的关系

3.2 结果与分析

实验过程中，训练、测试的时间与迭代次数、隐含层数成正比，继而选取木材纹理样本数NP=200，交叉概率CR=0.7，缩放因子F=0.02[14]进行实验，同时不同的隐含层节点数也将导致实验结果差异。经实验，当隐含层节点数设定为6时，分类器迭代计算次数增加，目标函数值将逐渐减少，当达到一定迭代次数时，目标值为0且保持不变(图8)。当隐含层数确定，随着迭代次数的增加，目标函数最小值越收敛[15]，当达到一定的迭代次数，目标函数最小值越稳定于0。而迭代次数一定时，隐含层的确定亦将影响着实验的完成时间，当迭代次数设定20时，增加隐含层数，可以降低算法的误差，但训练时间将拖长，差分演化优化极限学习机算法的分类时间随隐含层比例增长(表2)。在隐含层节点数为30时，DEELM算法达到误差最小点，并且趋于稳定。综上所述，选择隐含层数为30和迭代次数20的DEELM分类器进行分类。

根据上述的隐含层数和迭代次数，对实验初步选取木材纹理特征的样本进行实验，结果见表3；对于不同算法的性能比较见表4。

为了对比BP、SVM、ELM、DEELM 4种分类算法的准确率，实验重新选取直纹纹理和抛物纹纹理测试，训练样本个数分别为50、100、200、400。不同样本数目下准确率的分布见图9。

表2 隐含层数对算法的影响(迭代次数为20)

表3 木材纹理分类算法实验结果

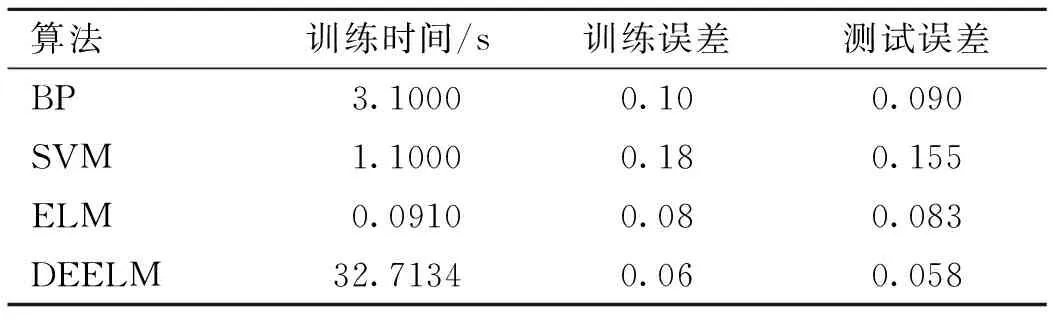
表4 不同算法性能比较

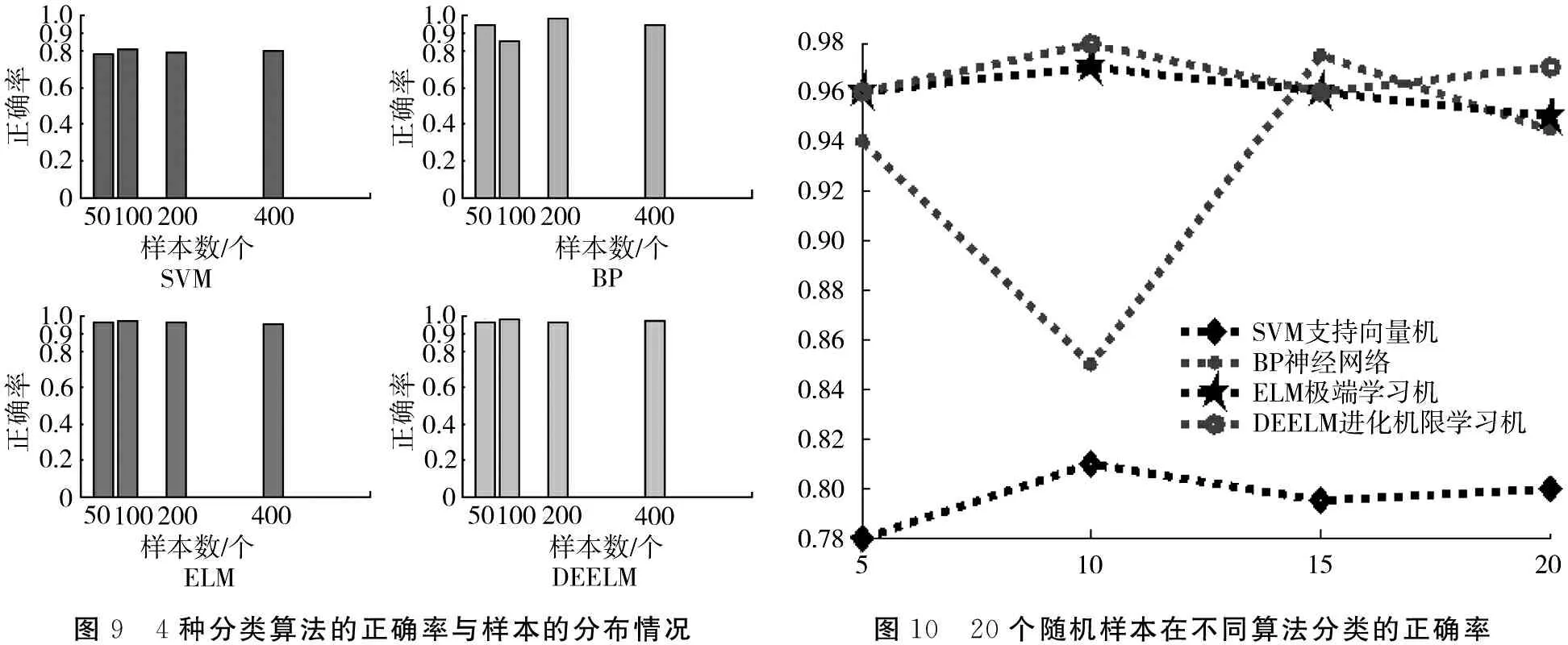
图9 4种分类算法的正确率与样本的分布情况图10 20个随机样本在不同算法分类的正确率

从图9可以看出，不同算法在处理不同样本数目的类别正确率明显不同，传统的BP较稳定，但是本文提出的DEELM算法在分类本次样本的效果明显优于BP神经网络[16]，而SVM支持向量机的分辨准确率不高。实验再次证明，DEELM分类器模型在木材纹理分类有一定的竞争性，效果明显。最后随机选取直纹、抛物纹纹理样本各10个，共计20个样本再次进行测试。进一步明确4种分类算法正确率的分布情况及走势(图10)，结果表明DEELM的分类效果相对最佳，分类显著。

4 小结

本文提出的基于差分演化优化极限学习机模型的木材纹理分类方法，采用旋转不变均匀模式下的LBP算子提取木材纹理特征，利用LBP特征矩阵作为输入参数，构建完整DEELM分类器模型。实验结果证明该算法适用于木材纹理分类，准确率高，效果明显优于传统BP神经网络、SVM支持向量机，具有一定的实用性。

[1]徐一清.木材纹理识别算法研究进展[J].大众科技，2010(8)：145-146.

[2]郭宝华，范少辉，官凤英，等.基于支持向量机的竹林信息提取研究[J].西北林学院学报，2014，29(2)：80-84.

[3]孙小添，邢艳秋，李增元，等.基于MODIS影像的决策树森林类型分类研究[J].西北林学院学报，2013，28(6)：139-144，168.

[4]Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：Theory and applications[J].Neurocomputing，2006，70(1-3)：489-501.

[5]贾丽媛，张弛.自适应差分演化进化算法[J].中南大学学报：自然科学版，2013，44(9)：3759-3765.

[6]Ojala T，Pietikinen M，Harwood DA.Comparative Study of Texture Measures with Classification based on Feature Distribution[J].Pattern Recognition，1996，1(29)：51-59.

[7]Ojala T，Pietikinen M，Mäenpää T.Multiresolution gray-scale and rotation invariant texture classification with Local Binary Patterns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(7)：971-987.

[8]Ojala T，Pietikäinen M，Mäenpää T.A generalized Local Binary Pattern operator for multiresolution gray scale and rotation invariant texture classification[C].Second International Conference on Advances in Pattern Recognition，Rio de Janeiro，Brazil，2001：397-406.

[9]袁菁穂.差分演化算法研究综述[J].高校理科研究，2013，29(1)：118-119，121.

[10]R S Phillip.Using a Differential Evolutionary Algorithm to Test the Efficient Market Hypothesis[J].Computational Economics，2012(40)：377-385.

[11]鄢靖丰.一种改进的自适应差分演化算法[J].许昌学院学报，2014，33(2)：74-77.

[12]Huang G B，Wang D.Advances in extreme learning machines(ELM2010)[J].Neurocomputing，2011，74(16)：2411-2412.

[13]Cao J W，Lin Z P，Huang G B.Self-Adaptive Evolutionary Extreme Learning Machine[J].Neural Processing Letters，2012，36(3)：285-305.

[14]蔺小林，邓雄峰.基于改进的DE算法对PID参数的优化[J].陕西科技大学学报，2014，32(1)：161-164.

[15]贺毅朝，王熙照，刘坤起，等.差分演化的收敛性分析与算法改进[J].软件学报，2010(5)：875-885.

[16]李康顺，李凯，张文生.一种基于改进BP神经网络的PCA人脸识别算法[J].计算机应用与软件，2014，31(1)：158-161.

Wood Texture Classification Algorithm Based on LBP-DEELM

XIANG Dong，CHEN Yu，CHEN Guang-sheng

(InstituteofInformationandComputerSciences，NortheastForestryUniversity，Harbin150040，Heilongjiang，China)

In order to deal with the issue of low categorization accuracy and tough calamity，a wood texture classification algorithm based on LBP-DEELM was proposed.On the basic of LBP operator and DEELM algorithm，combining the rotation invariant properties and original LBP operator，extracting the texture eigenvalues，combine the differential evolution algorithm to improve the efficiency of extreme learning machine，then get the parameters through training of different wood texture，establish a classifier，which achieves accurate and efficient wood texture classification.The experimental results show that the model error rate is about 2%，has higher accuracy and practicality than BP Neutral Networks，Support Vector Machine.

wood texture classification；LBP operator；DEELM；classifier

10.13428/j.cnki.fjlk.2015.04.012

2014-11-06；

2014-12-23

国家948项目(2011-4-04)；中央高校基本科研业务费专项资金项目(DL12CB02)；黑龙江省教育厅科学技术研究项目(12513016)；黑龙江省博士后基金

向东(1991—)，男，黑龙江哈尔滨人，东北林业大学信息与计算机工程学院硕士研究生，从事图像处理、模式分类的研究。E-mail：1062477258@qq.com。

陈宇(1975—)，男，黑龙江哈尔滨人，东北林业大学信息与计算机工程学院副教授，博士后，从事数学物理反问题求解，探测与成像，图像处理的研究。E-mail：nefu_chenyu@163.com。

S781.1；TP391.41

A

1002-7351(2015)04-0057-07