调整时间与顺序相关的能耗优化调度问题*

李冰，黎展滔（广东工业大学机电工程学院，广东广州510006）

调整时间与顺序相关的能耗优化调度问题*

李冰，黎展滔
（广东工业大学机电工程学院，广东广州510006）

以陶瓷行业车间生产计划为背景，将其抽象为调整时间与顺序相关的能耗优化调度问题进行研究。以最少化总能耗为目标，建立数学模型；提出了基于NEH算法的混合遗传算法，其中初始化种群中，定义了虚拟工件概念，采用了改进NEH规则对种群初始化；为了对上述算法进行验证，提出了该问题的两个下界，设计了仿真试验，进行下界背离程度分析和CPU运行时间分析。计算结果表明：所设计的混合遗传算法能够在可接受的计算时间内获得合理的解。

柔性流水车间；调整时间与顺序相关；遗传算法；能耗优化

0　引言

近十几年来，我国陶瓷工业得到了迅猛发展，然而，虽然我国陶瓷产量在世界上遥遥领先，但总体上存在能耗高、资源消耗大、综合利用率低、生产效率低等问题。开展以减少能源消耗为目标的调度方法研究，对提高能源利用率、减少企业生产成本具有重大意义。

陶瓷的生产过程中，当订单进行切换时，产生的调整时间导致了大量的时间成本和能耗成本。本文对陶瓷企业的调整时间分为两类：一类调整时间取决于工件顺序；另外一类调整时间取决于工件顺序和工件所在的机器。例如，对于成形工序，当需要切换不同的颜色时，其调整时间与订单的顺序相关；对于干燥工序，当订单需要切换时，工人们需要清洁机器，每台机器的清洗时间要取决于该机器在加工上一个订单时残留量的多少。因此，在干燥工序中，调整时间取决于订单的加工顺序和加工订单所在的机器。

近几年来，关于与调整时间相关的调度问题已经有许多的研究成果。Pinedo[1]指出如果处理不好，调整时间可以占用机器加工时间的20%。Cheng等人[2]，Potts and Kovalyov[3]等人和Allahverdi等人[4]对与调整时间相关的调度问题进行了综述。在这些文献中，把调整时间分为两类：调整时间与顺序相独立，即调整时间只与工件自身的相关；调整时间与顺序相关，即调整时间与工件之间的顺序相关。

本文以最少化能耗成本为目标，对具有两类调整时间与顺序相关的能耗优化调度问题进行了研究。针对该问题，提出了基于NEH规则的改进遗传算法。通过仿真实验，分析、验证比较了算法的有效性。

1　问题描述与数学模型

1.1问题描述

本文针对调整时间与顺序相关能耗优化调度问题进行了研究。该类问题的定义如下。

有n个工件或任务，每个工件都要先后经过k个阶段的加工。每个阶段由ms（s=1，2，…，k）台非同等并行组成。每台机器有三种模式：运行，待机和停止。对应着每台机器的三种模式，每台机器的能耗由三部分组成：运行能耗，空闲能耗和预热能耗。每个工件需要在每阶段中的一台机器上经过。工件不是同一时间到达，每个工件具有一个到达时间rj。在同一机器上连续加工的两个工件存在着调整时间。

1.2数学模型

n为工件数量；

k为阶段数；

rj为工件的投放时间，j=1，2，…，n；

ms为阶段s的机器数量，s=1，2，…，s；

pjhs为工件j在第s阶段的机器h上的加工时间，h=1，2，…，m；

Bjs为工件j在第s阶段开加工时间；

Cjs为工件j在第s阶段完工工时间；

ST1为调整时间与顺序相关的阶段集；

ST2为调整时间与工件顺序和工件所安排到机器相关的阶段集；

Qhs为安排在阶段s的机器h上加工的工件集；

ths为在阶段s机器h从停止状态到可以开始加工状态需要的时间；

Δths为在阶段s机器h上存在着空闲时间段的集合；

Δtwhs为在阶段s机器h上第w个空闲时间段，w∈Δtwhs；

M为一个足够大的整数；

决策变量：

数学模型如下：

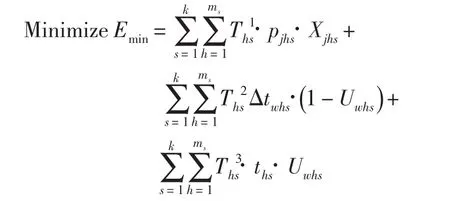
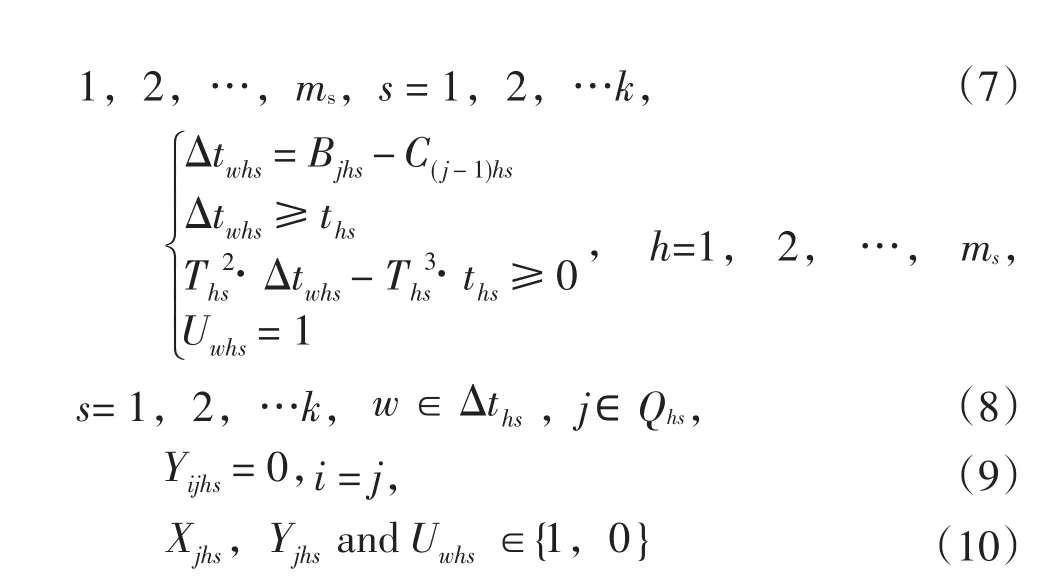
上述的表达式中：式（1）表示问题的目标函数，最少化总能源成本，总能耗Emin由三部分组成：运行能耗成本（即式（1）的第一部分），待机能耗（即式（1）的第二部分）和预热能耗（即式（1）的第三部分）；式（2）表示每个工件需要先后经过s阶段的加工，即每个工件在它上一阶段未加工完成前，不能开始在当前阶段的加工；式（3）表示工件在当期阶段的开始加工时间不能早于该工件在该阶段的投放时间；式（4）表示每个工件在同一时间只能安排在一台机器上加工；式（5）表示机器在同一时间只能加工一个工件。如果Yijhs=1，表示在阶段s机器h上工件j的开始加工时间大于工件i的完工时间，这意味工件i、j连续安排在阶段s的机器h上加工。如果Yijhs=0，则式（5）恒成立，其中M表示一个足够大的数目；式（6）计算工件在每阶段的完工时间，其完工时间等于工件在该阶段的开始加工时间加上工件在该阶段机器上的加工时间和调整时间。由于本文考虑了两类与顺序相关的调整时间，因此当当前阶段属于第一类调整时间时，工件在每阶段的完工有式（6）第一个表达式计算，否则，工件在每阶段的完工时间由式（6）第二个表达式计算；式（7）定义了工件在每阶段的开加工时间，其值等于工件在上一阶段的完工时间和工件安排在机器的可开始加工时间之间的较大值。当s= 1，Cjh(s-1)=rj和j=1，C0hs=0；式（8）确定在空闲时间段内机器的状态（待机状态或机器从停机到开机的预热状态）。式（8）第一表达式定义了机器存在空闲时间段的数量。如果满足式（8）第二和第三个表达式，则机器在该空闲时间段处于预热状态，否则机器处于待机状态。式（9）和（10）表示决策变量的取值范围。

2　基于NEH规则的混合遗传算法

2.1染色体表达

为了减少搜索空间中的冗余解，提高遗传算法搜索效率，可行解的染色体表达如下：编码的长度为n，等于被加工工件的数目，是工件集合的一个全排列，构成了各台机器的加工序列；各基因值代表相应工件所在的机器编号。编码分别表达了工件间加工顺序信息和工件与机器间分派信息[5]。

2.2种群的初始化

Nawaz等人[6]提出了一种NEH启发式算法。该算法被认为求解流水车间调度问题的最好启发式算法。NEH算法的核心思想是，工件的总加工时间越长，则该工件得到更高的加工优先级。NEH的算法步骤如下：

步骤1：根据工件总加工的减序进行排序，得到工件加工队列S；

步骤2：根据加工队列S，取其前两个工件进行调度得到最优调度；

步骤3：根据加工队列S读取下一个工件，把该工件插入到已经调度的工件排列中的某个位置，使得调度指标最少；

步骤4：重复上述过程，直到加工队列里的所有工件都调度完毕。

本文为同时考虑工件间的调整时间和加工时间提出一种基于NEH算法的基于调整时间和加工时间的能耗排序策略ESPRA。ESPRA算法的一个重要特征是引入了虚拟工件的概念。虚拟工件是由一对基于调整时间的最少能耗的工件组成，即每个虚拟工件由两个基于调整时间最少能耗的工件组成。虚拟工件的构建使得具有最少调整时间能耗工件组合在一起加工，减少工件在加工过程的调整时间。定义完虚拟工件后，本文还需要定义每个虚拟工件在每阶段的加工时间FJis，FJis的计算如式（11）所示。即，FJis等于虚拟工件中两个工件的基于工件加工时间的平均运行能耗成本。

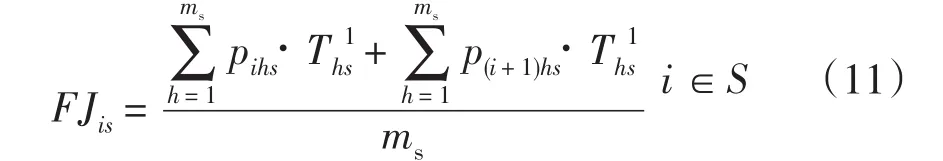
其中，p(n+1)hs=0。

假设J1，J2，…，J8为相互独立的工件，并且根据工件基于调整时间的总空闲能耗成本进行升序排列。FJ1s，FJ2s，FJ3s和FJ4s是虚拟的工件。例如，虚拟的工件FJ1s，由工件J1和J2，组成。根据公式（11）计算虚拟工件在阶段S上的加工时间。然后根据虚拟工件的加工时间减序对虚拟工件进行排序得到虚拟工件的加工队列。读取虚拟工件队列前两个工件进行最优调度，进而依次将剩余的工件逐个插入到已经调度的工件排列中的某个位置，使得总能耗成本最少，直到所有工件调度完毕，从而得到一个调度结果。例如，虚拟工件FJ1s和FJ2s具有两种可能的调度方案，即先加工FJ1s后加工FJ2s，或者先加工FJ2s后加工FJ1s。假设后者调度方案更优，那么得到工件局部调度方案，重复上述步骤直到所有虚拟工件调度完毕。得到初始化工件集合的全排列，各基因值取值randi(1，ms)，重复上述步骤，形成初始化种群。

2.3适应度函数和选择

由于优化目标为能耗最小，因此令目标函数的倒数为适应度值函数：f（i）=1/Emin。采用轮盘赌方法进行选择，在进化过程中个体的适应值越高，其被选择的概率就越大。

2.4交叉操作与变异操作

交叉在遗传操作中起核心作用，本文对染色体实行分段两点交叉操作，使得经过交叉后的染色体不破坏编码规则。本文对染色体实行分段变异操作，选择合适的变异概率，随机交换分段染色体中两个不同基因的位置。

3仿真试验

为了验证所提出的遗传算法的有效性，用MATLABr2012a仿真软件，并在CPU为Intel(R) Corei5-24502.5GHz，内存4G的计算机上进行仿真试验。

加工参数设置：柔性度m∈{1/3，2/3，1}；工件数目n∈{20，30，40，50，60，70，80，90}；调整时间与加工时间给出8个水平的比值：5%，10%，25%，50%，75%，100%，125%和150%。对应于这些比例，调整时间由以下均匀分布产生：U[1，5]，U[1，10]，U[1，25]，U[1，50]，U[1，75]，U[1，100]，U[1，125]和U[1，150]。单位时间运行能耗成本和单位时间空闲能耗成本由一个从1到10的随机数产生（即/=randi(1，10)）；每台机器单位时间的预热能耗成本由Ths3=randi(3，4)·Ths2产生，其中randi（3，4）表示一个从3到4的随机数。机器从停止状态到可加工状态的预热时间由产生，其中randi（0.1，0.5）表示一个由0.1到0.5的随机数。

遗传算法参数设置：种群规模100，交叉概率0.65，交换变异概率0.35，最大进化代数300。机器数目与工件数目的不同组合构成不同的问题规模；为消除随机因素对计算结果的影响，每种问题规模下产生50个计算实例，并报告平均计算结果，如表1所示，其中以背离程度来表达遗传算法计算目标值同最优解的差异，背离程度定义为（遗传算法计算目标值-下界）/下界。

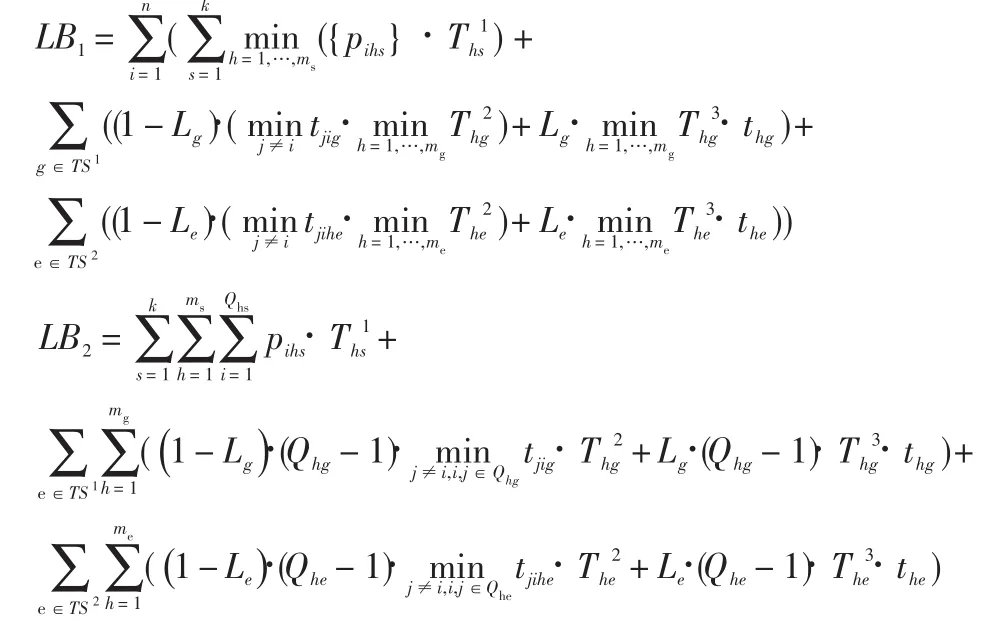
证明：

LB1：这是一个基于工件的定界。每个工件必须在每阶段上加工，并且需要调整时间。假设工件i在加工过程和调整时间时都是最少能耗成本，那么所有工件所得的总能耗成本为该问题的下界。基于这个思路，LB1的三个部分分别表示工件的最少运行能耗成本，最少待机能耗成本和最少预热能耗成本。

LB2：这是一个基于机器的定界。每台机器在每阶段的能源成本一共由三部分组成。LB2第一项表示机器的运行能耗成本，当调度方案确定时该部分能耗成本恒定不变。LB2第二项表示机器在调整时间为第一类调整时间的最少空闲能耗成本，其中，对于阶段g的机器h，至少存在(Qhg-1)段空闲调整时间段。如果每一段都取最少调整时间，则机器在该阶段的空闲能耗成本最少化。同理，LB2第三项表示当机器属于第二类调整时间时，机器空闲能耗成本的下界。

表1　数值计算结果

从表1中可看出，遗传算法计算目标值同下界的最大和最小平均背离程度分别为1.852%和0.2395%。随着问题规模的增长，遗传算法平均运行时间、计算目标值同下界平均背离程度的变化趋势分别如图1、图2所示，其中算法运行时间基本呈现线性增长的趋势，而背离程度的增长趋势趋于平缓。

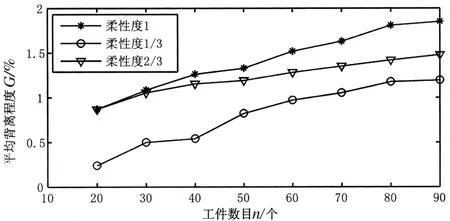
图1　计算目标值同下届背离程度变化曲线

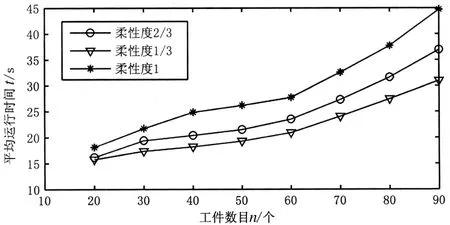
图2　遗传算法运行时间变化曲线

4　结论

（1）以能耗为目标，对调整时间与顺序相关的柔性流水车间调度中的工件分配与排序进行决策，提出了该问题的数学规划模型，并解析证明了该问题的一个下界。

（2）同时考虑工件间的调整时间和加工时间提出一种基于NEH算法的基于调整时间和加工时间的能耗排序策略，并提出了基于NEH算法的混合遗传算法。

（3）进行试验分析，通过与引入的下界进行比较，表明了设计的遗传算法具有较好的求解性能，能够在较短的时间内获得满意解。

参考文献：

［1］Pinedo M.L..Scheduling theory，algorithms and sys⁃tems［M］.Upper Saddle River，New Jersey：Pren⁃tice-Hall.2008.

［2］Cheng T.C.E.，Gupta J.N.D.，Wang G.Q.A review of flowshop scheduling research with setup times［J］. Production and Operations Management，2000，9（3）：262-282.

［3］Potts C.N.，Kovalyov M.Y.，Scheduling with batch⁃ing：a review［J］.European Journal of Operational Research，2000，120（2）：228-249.

［4］Allahverdi A.A survey of scheduling problemswith setup timesor costs［J］.European JournalofOperationalRe⁃search，2008，187（3）：985-1032.

［5］廖珊，翟所霞，鲁玉军.基于改进遗传算法的柔性作业车间调度方法研究［J］.机电工程，2014（6）：729-733.

［6］Nawaz，M.，Enscore，E.，Ham，I.，A heuristic algorithm for them-machine n-job flow shop sequencing problem［J］.Omega，1983，11（1）：11-95.

(编辑：阮毅)

Energy Consumption Optimization Scheduling Problem with Sequence-Dependent Setup Times

LI Bing，LI Zhan-tao
（Guangdong University of Technology，CollegeofMechanicaland Electronic Engineering，Guangzhou 510006，China）

This paper considers ceramic industry workshop production plan as the background，abstract that to energy consumption optimization scheduling problem with two types of sequence-dependent setup times to study.Tominimize the total energy consumption as the goal，establishmentofmathematicalmodel.The hybrid genetic algorithm is proposed based on NEH algorithm，in the initialization of population，defines the concept of virtual work，using the improved NEH rules for population initialization.Two lower bounds are proposed to evaluate the algorithms.A computational experiment is developed to lower bounds degree of deviation analysis and CPU running times analysis.The analysis reveals that designed by hybrid genetic algorithm can be acquired within an acceptable computation time reasonable solution.

flexible flow shop；sequence-dependentsetup time；Genetic algorithm；energy consumption

TH165 TP301

A

1009－9492(2015)06－0012－05

10.3969/j.issn.1009-9492.2015.06.003

*广东省自然科学基金资助项目（编号：501130093）；粤港澳领域重点突破项目（编号：2012A080107017）

2015－03－18

李冰，男，1990年生，江西吉安人，硕士研究生。研究领域：智能制造、绿色制造、制造物联网。