遗传算法在电力维护人员调度问题中的应用

王柏根，汪　勋，张子臻

遗传算法在电力维护人员调度问题中的应用

王柏根1，汪勋2，张子臻2

（1.东莞供电局，东莞523000；2.中山大学移动信息工程学院，珠海519000）

随着电力设备的不断发展和电力需求的不断增加，电力维护问题日益突出。如何合理安排电力维护人员的行程成为一个亟待解决的问题。将该问题建模为累积时间的带容量的车辆路径问题的模型。CCVRP是传统车辆路径规划问题的一个变种，但与一般VRP不同的是，它以最小化客户的总等待时间为目标。针对该问题，我们利用遗传算法的框架，并结合模拟退火算法进行局部搜索对问题进行求解。实验部分证明该方法能有效地解决该类优化问题。

累计时间；车辆路径规划问题；遗传算法；模拟退火

中央高校基本科研业务费专项资金（No.15lgpy37）

0　引言

电力工业是国民经济的重要基础产业，电力设施是电能生产、输送、供应的载体，是重要的社会公用设施。电力设施的日常维护是保障供用电安全和维护社会公共安全的基础性工作。在电力发展日益迅猛的今天，电力系统网络越来越复杂，电力系统的安全性问题也逐渐突出。面对成百上千个分布在城市各处的电力设备，需要考虑维护人员工作的优化问题。本文的问题正是源于某市供电局的实际情况。其问题可以描述为，假设A供电局有n个分布在各地的电力设备（用集合N={1,…,n}表示）和m个维护人员，每个电力设备在得到维护前的等待时间为该问题就是如何安排这m个维护人员的工作路径，使得在满足维护人员最大工作量的前提下让最小。其中等待时间主要与维护人员行走的路程有关。

这个问题我们可以把它抽象为以最小化客户的总等待时间为目标的“累积时间的带容量的车辆路径问题”（The Cumulative Capacitated Vehicle Routing Problem）问题，该问题是VRP（Vehicle Routing Problem）问题的延伸。VRP最早是由Dantzig和Ramser于1959年首次提出，它是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是在满足所有客户的需求且在满足一定的约束下，达到路程最短、成本最小、耗时最少等目的。VRP已被证明是一个NP难问题。

CCVRP也是一个NP难问题，传统的精确求解方法例如分支定界法难以解决大规模的数据，因此一般采用启发式算法。例如文献[1]就采取了一种Memetic Algorithm的进化算法，由于解决CCVRP的案例不多，所以本文的实验结果也主要与[1]对比；文献[2]采取了一种变邻域搜索的方式；文献[3]采用了大邻域搜索方法；文献[6]则主要是一种加入了贪心的禁忌搜索。本文的求解方法是前期利用遗传算法[10]的快速收敛性，查找最优解集空间，后期再结合用模拟退火[4]，进行细致的局部搜索，从而找到较优的问题的解。

1　数学模型的建立

我们把n个分布在各地的电力设备看作CCVRP问题中的服务点,m个维护人员看作CCVRP中的车辆，可描述如下：在图G=（V，E）中，服务点集合为{0，1，2，…，n}，R表示安排的车辆集合，Q表示车辆的容量限制，表示从i到j的花费，tik表示第k辆车到达i的时间花费，xkij是一个布尔值，如果它是1，说明第k辆车经过了（i，j）这条边，反之则表示没有经过，有如下整数规划模型：

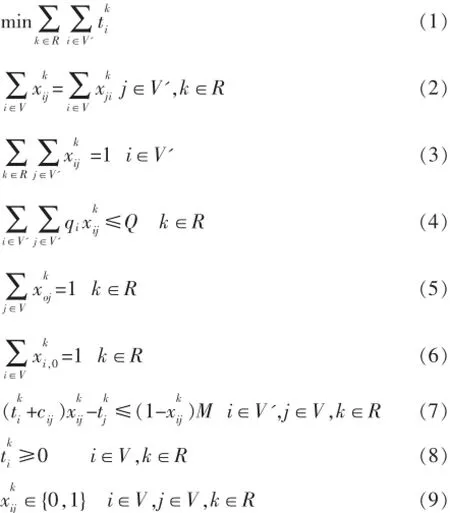
其中（1）是保证得到最小目标函数值，（2）保证派出去的车都能回来，（3）保证每个客户都只被服务一次，（4）保证每条路线上车的运输量都不超过容量限制，（5）跟（6）保证每条路径都以0为起点和终点，（7）保证当j在i后被车辆k服务，则比大，M是一个足够大的值，目的是防止出现环路。

2　算法的实现

2.1设计思路

文献[1]中采取的Memetic Algorithm算法是每次遗传迭代后都采用一次局部搜索。为了找到全局最优解，在初期需要有较大的概率接受差解。这样一来，初期与单纯使用遗传算法所得到的种群质量差别并不是很大，可是时间花费却加大了。所以我们在前期只是单纯使用遗传算法，利用它的快速收敛性，找到较优的解集，而在后期遗传算法效率下降的时候，我们采用一边迭代一般局部搜索（模拟退火[4]）的方式。对于何时该加入局部搜索，程序每次用遗传算法迭代都记录下种群的最优解，当出现连续多次最优解没有明显提高的时候，就进入算法的下一步（本文是用连续四次的方差来衡量）。

实验结果表明，采用这种方式可以得到较好的结果，在时间开销上也有了较好的表现。

2.2遗传算法

遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。它采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。它是现代有关智能计算中的关键技术。其基本运算过程如下：

（1）初始化种群：设置进化代数计数器N=0，设置最大进化代数M，产生M个个体作为初始化种群P（0）。

（2）个体评价：计算群体P（N）中各个个体的适应度。

（3）选择运算：对当代种群群体进行选择。选择的目的是把适应度更高的个体遗传到下一代或选择它们进行交配从而产生适应度较高的子代遗传到下一代。

（4）交叉运算：选取两个或者多个种群内的个体进行交叉运算。这是遗传算法的核心步骤。

（5）变异运算：对种群内的每个个体以一定的几率进行变异，以达到跳出局部最优解的作用。

经过选择、交叉、变异后得到下一代种群P（N+1）。

（6）如果N==M，程序终止，否则N=N+1，返回步骤（2）。

本文中采用的遗传算法和上述步骤基本一致，但在初始化种群，算子概率的确定以及选择策略上有所改进，使效果更好。

其中，初始化过程没有采取随机化，而是带有一定的策略，获得较为优秀的初始群体，算子概率的确定则是采取了自适应的动态变化方式，选择策略也放弃了传统的轮盘赌，采取了竞争选择的方式。下文还会详细论述。

2.3基因编码

采用整数编码的形式对它进行编码，不同的排列方式代表不同的路径安排，再设计适应度函数对不同的路径进行划分。假设有n个客户，那么（1，2，…，n）表示顺序服务客户1~客户n。

2.4计算适应度

根据编码方式，我们在满足限制条件的前提下采用文献[10]介绍的一种划分路径方式，运用动态规划的思想，每次增加一辆车后，都对每个节点进行一次松弛，该算法的复杂度为O（n2）。

以车辆的最大数目为3，最大服务量为10为例。

①如图1所示，小括号中数字表示该点需要的服务量。

图1　

②当只有一辆车的时候，最多只能到达b节点，用Pki记录在第k次迭代过程中0~i节点的最优路径，方框内表示到当前节点的最短距离。

图2　

③继续增加车辆，对以上一轮经过的节点进行更新（如b节点的值被更新为45）。

图3　

④重复上述步骤，直到结束。

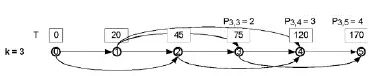
图4　

得出最优路径。

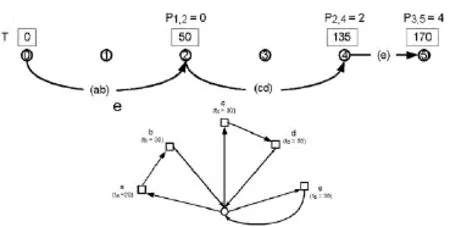
图5　

2.5种群初始化

由经验可知，一辆车集中访问一片区域往往可以得到较优的解集，如下图所示：

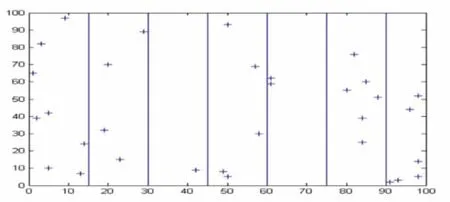
图6　

以笛卡尔坐标系为例，我们把每个坐标点按照x坐标由小到大排序，将排序后的数列作为种群的初始解，以此获得质量较高的第一代种群。

2.6交叉

在交叉与变异的概率的确定上，我们采取了自适应的概率计算方式，公式如下：

Pc表示交叉概率，其中Pc1=0.9，Pc2=0.6

Pm表示变异概率，其中Pm1=0.1，Pm2=0.001

favg表示种群的平均适应度

fmax表示需要交叉的两个个体中适应度较大的那个值

f表示被选择个体的适应度

这样，我们可以保证适应度较大的个体有较小的交叉和变异概率，从而在竞争选择的过程中被很好地保存下来。

交叉方式选择了比较经典的匹配交叉（PMX），我们先随机产生两个交叉点，定义这两点间的区域为匹配区域，并用交换两个父代的匹配区域。

父代A：872|130|9546

父代B：983|567|1420变为：

TEMP A:872|567|9546

TEMP B:983|130|1420

对于TEMP A、TEMP B中匹配区域以外出现的数码重复，要依据匹配区域内的位置逐一进行替换。匹配关系：1〈—〉5，3〈—〉6，7〈—〉0。得到匹配后的结果如下所示：

子代A：802|567|9143

子代B：986|130|5427

2.7种群选择

实验初期采用的是传统的轮盘赌策略，结果发现这种策略的效果并不理想。所以我们采取了竞争选择的策略，主旨思想就是每次从种群里任意选择两个种群，选择当中较大的那个代入下一次迭代过程（假如遇到相同的则都不选择），然后再将其全部放回，重复这一步骤直到选择完成。

2.8局部搜索和变异

局部搜索我们采用的是文献[4]中的模拟退火方式，选择了较低的初始温度t0=30以及L=1000的马尔可夫链长，以e（-ΔE/kt）的概率接受新解（ΔE为新解与原始解的适应度大小的差值），其产生新解的方式和变异的方式一致，都有下面两种：

（1）2-opt

随机选取两点i和j，将i之前的路径和j之后的路径不变地添加到新路径中，将i到j之间的路径翻转其编号后添加到新路径中。例如原路径为ABCDEFG，若我们随机选取的区间为（CDEF），则进行2-opt操作后得到的新路径为ABFEDCG。

（2）随机产生三个位点，将1，2位点间的基因与2，3位点间的基因左右交换。例如对于路径ABCDFE，我们选择了ACF这三个位点，执行交换后得到新路径ADCBF。

实验初期还采取了随机交换两个点位置的这种变化策略，但实验过程中发现这并没有提高解的质量。

3　程序框架

程序的大体框架如下：generation〈—0

initial（）//初始化种群

while（generation〈maxgeneration）C

hoose（）//选择交叉的子代C

rossover（）//子代交叉产生新的子代Mutation（）//子代变异产生新的子代

If（judge（））//根据前几次方差判断遗传算法的收敛速度，如果速度较慢，就开始调用局部搜索

Localsearch（）//用模拟退火进行局部搜索，更新子代

endIf

Preservethebest（）//保存最优解

endwhile

4　实验及运行结果

我们使用C编程，程序运行环境为i3处理器，2.30GHz，4GB内存，64位Win7操作系统，而文献[1]中也是用C编程，程序运行环境为3.4GHz，1GB内存，WinXP操作系统。测试了文献[1]中的数据。

文献[1]中Table 1作者的数据是从文献[6]中获得。其解决的主要是TRP问题，TRP问题则是在TSP问题上求解最小路径和的变式，也就是本文所求的CCVRP问题的特例（其车辆数为1）。

文献[1]中的作者是用实验数据的下界与实际实验数据来计算相差的百分比，从而进行度量，而且只考虑用一种车的情况。其下界的计算方法是构建n个点的最小生成树。那么有：

其中，wi是将这棵最小生成树的边按照升序方式排序后第i条边的权值。其中，作者给出了范围为10~ 500这6种规模的数据，每个数据规模又有20个算例。实验结果如表1所示，注意相差的比例是20个算例的平均值与下界的差距，可以看出，我们的结果与文献[1]的结果差距不大。

表2是与文献[1]中的Table 3做的比较，文献采取的方法是利用TSP问题的数据（数据来源：http://www.iwr.uniheidelberg.de/groups/comopt/software/TSPLIB95/），不考虑容量限制，给出固定车辆数生出CCVRP的算例。由该表同样看出我们的算法表现同样较好。

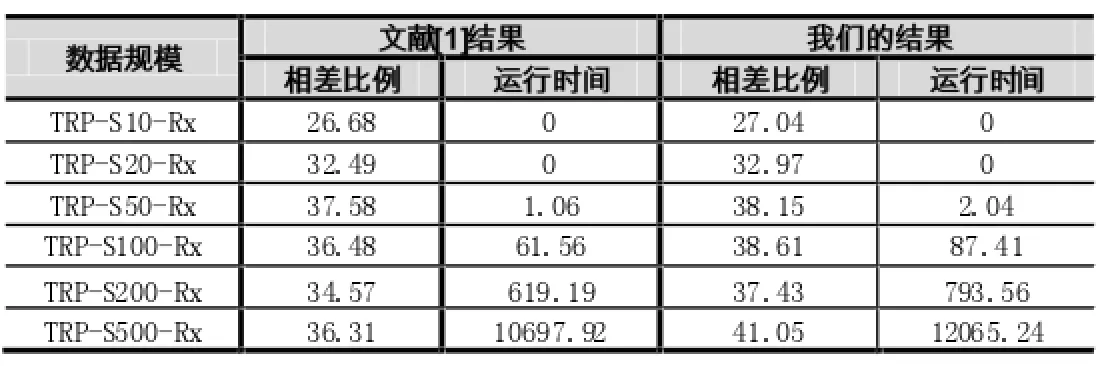
表1　TRP实验对比结果

表2　CCVRP结果

另外，我们还利用某市供电局的变压器分布数据，随机选取41个点，对5个工作人员进行任务指派。得出的效果图如图7所示。

图7　实际效果图

5　结语

本文研究了电力维护人员调度问题，并把它建模为累积时间的带容量的车辆路径问题（CCVRP）。我们给出了一种用利用遗传算法对CCVRP进行求解的方法，并结合模拟退火算法对局部解进行了优化。实验表明我们的求解结果与对比文献差距不大。同时，我们用实际电力维护的数据对算法进行测试，因此该方法具有较强的实际意义。

[1]Ngueveu S U，Prins C，Calvo R W.An Effective Memetic Algorithm for the Cumulative Capacitated Vehicle Routing Problem[J]. Computers&Operations Research，2010，37（11）:1877~1885

[2]Croes G A.A Method for Solving Traveling-Salesman Problems[J].Operations Research，1958，6（6）:791~812

[3]Ribeiro G M，Laporte G.An Adaptive Large Neighborhood Search Heuristic for the Cumulative Capacitated Vehicle Routing Problem [J].Computers&Operations Research，2012，39（3）:728~735

[4]Osman I H.Metastrategy Simulated Annealing and Tabu Search Algorithms for the Vehicle Routing Problem[J].Annals of Operations Research，1993，41（4）:421~451

[5]Gendreau M，Hertz A，Laporte G.A Tabu Search Heuristic for the Vehicle Routing Problem[J].Management Science，1994，40（10）: 1276~1290

[6]Salehipour A，Sörensen K，Goos P，BRAYSY，O.An Efficient GRASP+VND Metaheuristic for the Traveling Repairman Problem[R]. University of Antwerp，Faculty of Applied Economics，2008

[7]Campbell A M，Vandenbussche D，Hermann W.Routing for Relief Efforts[J].Transportation Science，2008，42（2）:127~145

[8]Barbarosoglu G，Ozgur D.A Tabu Search Algorithm for the Vehicle Routing Problem[J].Computers&Operations Research，1999，26（3）:255~270

[9]Hiquebran D T，Alfa A S，Shapiro J A，et al.A Revised Simulated Annealing and Cluster-First Route-Second Algorithm Applied to the Vehicle Routing Problem[J].Engineering Optimization，1993，22（2）:77~107

[10]Prins C.A Simple and Effective Evolutionary Algorithm for the Vehicle Routing Problem[J].Computers&Operations Research，2004，31（12）:1985~2002

[11]Croes G A.A Method for Solving Traveling-Salesman Problems[J].Operations Research，1958，6（6）:791~812

[12]李宁馨.采用不同算法求解车辆路径问题的对比分析[J].重庆工商大学学报（自然科学版），2014，5:016

王柏根，男，工程师，工学学士，研究方向为计算机应用与工程管理

汪勋，男，本科，研究方向为算法设计与分析

张子臻，男，讲师，研究方向为最优化理论、人工智能

Cumulative Time;Capacitated Vehicle Routing Problem;Genetic Algorithm;Simulated Annealing

Application of Genetic Algorithm in Scheduling Problem of Maintaining Electric Metering Devices

WANG Bo-gen1，WANG Xun2，ZHANG Zi-zhen2

（1.Power Grid Co.，Guangdong Dongguan Power Supply Bureau，Dongguan 523000）（2.School of Mobile Information Engineering，Sun Yat-Sen University，Zhuhai 519000）

With the rapid development of the power equipment and demand,electricity maintenance issues become increasingly prominent.How to arrange the maintenaners into a timely power optimization problem needs to be solved.Aiming at this problem,proposes a model called the Cumulative Capacitated Vehicle Routing Problem.CCVRP is a variation of the classical Capacitated Vehicle Routing Problem in which the objective is to minimize the sum of waiting times at customers.Establishes a genetic algorithm combined with a simulated annealing algorithm for local search.Experiments indicate that the algorithm is able to solve the problem effectively.

1007-1423（2015）12-0003-06

10.3969/j.issn.1007-1423.2015.12.001

2015-03-17

2015-04-09