不定方程x3-1=PQy2的整数解
2015-09-16李润琪德宏师范高等专科学校数学系云南芒市678400
李润琪(德宏师范高等专科学校数学系,云南芒市678400)
不定方程x3-1=PQy2的整数解
李润琪
(德宏师范高等专科学校数学系,云南芒市678400)
主要利用同余式、二次剩余等证明了P≡19(mod 24)为奇素数,Q=97 241 337时,不定方程x3-1=PQy2仅有整数解(x,y)=(1,0).
不定方程;整数解;同余;二次剩余
不定方程

是一类重要的三次方程,其整数解已有不少人研究过.当D>2,D无平方因子且不含6k+1形素因子时,文献[1,2]已经解决;当D含6k+1形素因子时,目前已有许多相关结论,但是D含两个或两个以上6k+1形素因子时,方程(1)的求解较为困难,目前结论还比较少.文献[3]给出D=pq,p≡1(mod 24)为奇素数,q=12s2+1为奇素数时方程(1)的解的情况;文献[4]给出D=pq,p=73,q≡1,19(mod 24)为奇素数,时方程(1)的解的情况;文献[5]给出D=pq,q=13,p≡1(mod 12)为奇素数时方程(1)的解的情况;文献[6]给出D=pq,p=7,q=13,19,61时方程(1)的解的情况;文献[7]给出D=pq,q=7,为素数时方程(1)的解的情况;文献[7]给出D=1267=7×181时方程(1)的解的情况.此处主要研究P≡19(mod 24)为奇素数时方程(1)的解的情况.
引理1[8]设p≡19(mod 24),q≡1(mod 24),p,q为奇素数,则丢番图方程组x-1=3pqu2,x2+x+1=3v2,gcd(u,v)=1只有平凡解(x,u,v)=(1,0,±1).
定理1设P≡19(mod 24)为奇素数,Q=97 241 337,勒让德符号值,则不定方程

仅有平凡解(x,y)=(1,0).
证明因为x3-1=(x-1)(x2+x+1),而gcd(x-1,x2+x+1)=gcd(x-1,(x-1)2+3(x-1)+3)=gcd(x-1,3)=1或3,故方程(2)给出以下8种可能的分解:
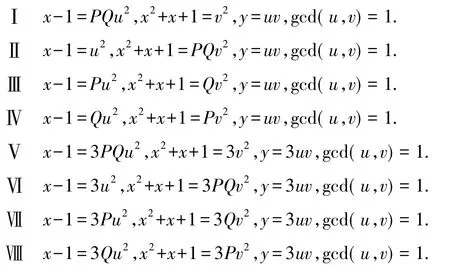
以下讨论这8种情况所给的方程(2)的整数解.
情形Ⅰ解x2+x+1=v2,得x=0,-1,均不适合x-1=PQu2,故方程(2)在该情形无整数解.
情形Ⅱ将x-1=u2代入x2+x+1=PQv2得(2u2+3)2+3=4PQy2,则有

当Q=97时,有(2u2+3)2≡-3≡262(mod 97),得u2≡34,60(mod 97),但模97的勒让德符号值为故式(3)不成立,因此此时方程(2)无解.
当Q=241时,有(2u2+3)2≡-3≡312(mod 241),得u2≡17,227(mod 241),但模241的勒让德符号值为,故式(3)不成立,因此此时方程(2)无解.
当Q=337时,有(2u2+3)2≡-3≡802(mod 337),得u2≡130,210(mod 337),但模337的勒让德符号值为故式(3)不成立,因此此时方程(2)无解.
综上,有方程(2)在该情形无整数解.
情形Ⅲ因为P≡19(mod 24),有x=Pu2+1≡1,4,5(mod 8),则x2+x+1≡3,5,7(mod 8).又Q=97,241,337,则有Qv2≡1(mod 8),矛盾.故方程(2)在该情形无整数解.
情形Ⅳ将x-1=Qu2代入x2+x+1=Pv2,得(2Qu2+3)2+3=4Pv2,则有3≡Pv2(mod Q).又Q=97,241, 337,则勒让德符号值而勒让德符号值,矛盾.故方程(2)在该情形无整数解.
情形Ⅴ因为P≡19(mod 24),Q=97,241,337≡1(mod 24),故由引理1知方程(2)在该情形仅有平凡解(x,y)=(1,0).
情形Ⅵ因为x=3u2+1≡1,4,5(mod 8),则x2+x+1≡3,5,7(mod 8).又P≡19(mod 24),Q=97,241,337,则PQ≡3(mod 8),3PQv2≡1(mod 8),矛盾.故方程(2)在该情形无整数解.
情形Ⅶ将x-1=3Pu2代入x2+x+1=3Qv2,得(6Pu2+3)2+3=12Qv2,则有1≡Qv2(mod P).又勒让德符号值,矛盾.故方程(2)在该情形无整数解.
情形Ⅷ将x-1=3Qu2代入x2+x+1=3Pv2,得(6Qu2+3)2+3=12Pv2,则有1≡Pv2(mod Q).又勒让德符号值,矛盾,故方程(2)在该情形无整数解.
综上,有不定方程(2)在题设条件下仅有平凡解(x,y)=(1,0).
[1]柯召,孙琦.关于丢番图方程x3±1=3Dy2[J].四川大学学报,1981,18(2):1-5
[2]柯召,孙琦.关于丢番图方程x3±1=Dy2[J].中国科学,1981,24(12):1453-1457
[3]管训贵,杜先存.关于Diophantine方程x3±1=pqy2[J].安徽大学学报:自然科学版,2014,38(1):13-19
[4]杜先存,管训贵,杨慧章.关于不定方程x3-1=73qy2的整数解[J].西南师范大学学报:自然科学版,2014,39(6):18-20
[5]管训贵,杜先存.关于丢番图方程x3-1=13py2的整数解[J].沈阳大学学报:自然科学版,2014,25(6):511-513
[6]管训贵.关于丢番图方程x3±1=7qy2的整数解[J].兰州文理学院学报:自然科学版,2014,28(2):20-24
[7]杜先存,万飞,杨慧章.关于丢番图方程x3±1=1 267y2的整数解[J].数学的实践与认识,2013,43(15):288-292
[8]杜先存,管训贵,万飞.关于Diophantine方程组x-1=3pqu2,x2+x+1=3v2的整数解[J].重庆师范大学学报:自然科学版,2015,32(1):102-105
On Integer Solution to the Indefinite Equation x3-1=PQy2
LIRun-qi
(Department of Mathematics,Dehong Teachers College,Mangshi 678400,China)
Using congruence and quadratic residue,this paper proves that P≡19(mod 24)is odd.When Q=97 241 337 and,the indefinite equation x3-1=PQy2only has integer solution.
indefinite equation;integer solution;congruence;quadratic remainder
O156.2
A
1672-058X(2015)09-0045-03
10.16055/j.issn.1672-058X.2015.0009.012
2015-01-15;
2015-02-20.
云南省教育厅科学研究项目(2014Y462).
李润琪(1965-),男,云南腾冲人,讲师,从事初等数论及数学教育研究.
