多自由度结构静风响应的GPU并行计算

杨智诚+饶瑞

摘要： 根据某大型双层柱面网壳风致静力响应计算的有限元模型，建立基于GPU的MATLAB快速并行计算平台，实现CUDA框架下多自由度结构风致静力位移响应的快速求解.数值计算表明，与传统的CPU串行计算相比，通过GPU实现的大型矩阵的求逆、乘法、除法等运算速度得到大幅提高，位移计算获得23倍的最大加速比；结果误差对比分析也表明基于GPU的计算结果能够满足工程精度要求.

关键词： 双层网壳； 风致静力响应； 节点位移； GPU； MATLAB； CUDA

中图分类号： TU311.1文献标志码： B

Abstract： According to the finite element model which is built for the calculation of static windinduced response of a largescale doublelayer cylindrical reticulated shell， a fast parallel computing platform is built in MATLAB by GPU， and the fast solution for the windinduced static displacement responses is implemented with the frame of CUDA. The numerical calculation indicates that， compared with the traditional serial computing of CPU， the calculation speed of the operation of inversion， multiplication， division of large matrix is greatly improved， and the maximum speedup ratio of displacement calculation is improved by 23 times. The comparison and analysis on the errors show that the results based on GPU calculation can meet the accuracy requirements of engineering projects.

Key words： doublelayer reticulated shell； static windinduced response； nodal displacement； GPU； MATLAB； CUDA

收稿日期： 2015[KG*9〗03[KG*9〗26修回日期： 2015[KG*9〗04[KG*9〗22

基金项目： 广州市属高校“羊城学者”项目（12A004S）； 高等学校博士点基金（博导类）（20124410110005）； 珠江科技新星专项（2012J2200093）

作者简介： 杨智诚（1992—），男，广东湛江人，硕士研究生，研究方向为结构抗风设计，（Email）328157170@qq.com0引言

随着现代建筑结构的复杂程度越来越高，采用有限元法进行结构分析时，大量自由度导致大型高阶刚度矩阵出现.在结构位移响应的求解计算过程中，大型矩阵运算成为影响计算效率的瓶颈.MATLAB是目前工程计算中自编程序的主流工具，可通过矩阵求逆或左除求解结构静力响应，但大型矩阵常使该类计算在普通电脑上出现因内存溢出而无法计算或耗时较长等问题.

基于GPU的并行计算是指在NVIDIA公司推出的统一计算设备架构（Compute Unified Device Architecture，CUDA）下，通过调用GPU多线程和函数库完成单指令的并发执行，以实现大数据快速处理的计算方法.[1]与传统的串行计算相比，使用GPU并行计算能够大幅度提高计算效率且在普通个人电脑上就能实现.MATLAB的主要计算模式是基于CPU的串行计算，为充分利用GPU的计算优势，其2010b版本开始支持GPU计算.[2]刘绍波等[3]实现MATLAB在CUDA框架下对GPU扩展使用，并应用于岩土工程计算.张健飞等[4]将GPU应用于有限元计算中，在CUDA框架下实现预处理共轭梯度法求解大规模线性方程组.

本文基于某大跨双层柱面网壳结构（杆件总数为10 080个）的风致静力位移求解的有限元模型，研究在MATLAB平台上通过GPU加速大型结构静力响应求解的方法，并分析不同算法的求解效率和误差.

1工程背景和需加速函数的定位

1.1工程背景

某发电厂干煤棚为双层柱面网壳结构，纵向长度为140 m，横向跨度为103 m，高为40 m，沿纵向边缘为刚性支承，见图1.该结构为正放四角锥柱面网壳，杆件总数和节点总数分别为10 080和2 592个，杆件弹性模量为206 GPa，密度为7 850 kg/m3.基于风洞实验获得某一典型风向角下的实际风压时程[56]，在此基础上计算等效静力风载荷[7].

根据有限元法，结构的节点位移求解公式[8]为U=K-1·F（1）式中：U为节点位移矩阵，阶数为7 776×1，即结构总自由度数为7 776；K-1为总体刚度矩阵的逆矩阵，阶数为7 776×7 776；F为节点的等效静力风载荷.

MATLAB的相应实现代码为U=inv（K）*F （2）式中：inv为MATLAB求逆函数.

1.2确定需加速的函数

在MATLAB平台上编制相应有限元计算程序，包含以下主要步骤.

1）读入相关数据，如节点数、节点坐标数组、节点力数组等.

2）计算节点力数组F.

3）计算单元刚度矩阵k，函数名为SpaceTrussElementStiffness.

4）组装总体刚度矩阵K，函数名为SpaceTrussAssemble.

5）引入边界条件[9]，并计算节点位移矩阵U.

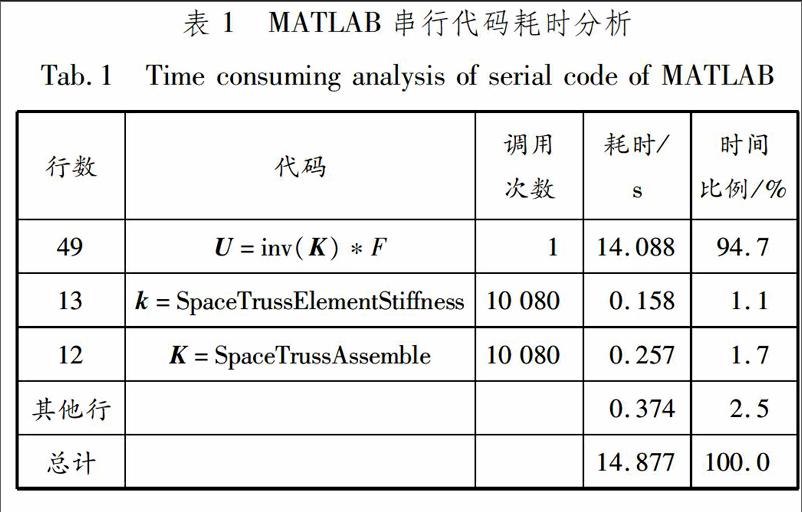
通过MATLAB的代码效率调试工具Profiler获得主要函数的运行时间、调用次数等信息，统计耗时前3位的函数，包括代码行序、函数名称、调用次数、总耗时及占整个耗时的比例，见表1.显然，计算节点位移﹝式（2）﹞的运行时间最长，占总计算时间的94.7%，因此考虑将最耗时部分交由GPU实现，从而提高求解速度.

次数耗时/

s时间

基于GPU的求解将通过2种方式实现：

1）将串行代码中的矩阵求逆与乘法分别交由GPU实现，主要代码为K-1=g_inv（K）

U=g_mul（k_inv，F） （3）式中：g_inv和g_mul均为自编的调用GPU实现矩阵运算的函数；g_inv为矩阵求逆运算；g_mul为矩阵乘法运算.

2）将矩阵求逆和乘法转换为矩阵除法，然后将矩阵除法交由GPU实现，主要代码为U=g_div_l（K，F） （4）式中：g_div_l为自定义的调用GPU实现矩阵左除的函数.

通过以上2种方法实现在GPU下的并行求解.

2GPU算法实现

2.1软硬件环境

计算在普通个人电脑上完成，其基本配置如下.

在MATLAB平台上，可以自编多线程CUDA程序或调用NVIDIA公司提供的函数库（如CUBLAS和CULA）实现GPU加速.自编CUDA程序在VC平台下编写，因此需要实现CUDA程序与MATLAB的对接.NVIDIA公司提供NVMEX插件，使得在MATLAB平台上能够编译CUDA程序，以生成可被MATLAB调用的动态链接库.

2.2算法实现

2.2.1矩阵乘法

基于GPU的矩阵乘法主要通过调用CUBLAS函数库实现，其中包含大量已经编写好的关于线性代数运算的程序.

首先在CUDA程序中编写MEXFunction接口函数，将MATLAB中需要处理的数据传入CUDA程序，再调用CUBLAS函数库中的CUBLASSgemm函数实现矩阵相乘.根据NVIDIA CUBLAS Library文档说明，该函数主要进行的运算是C=αAB+βC（5）式中：A和B为待相乘的矩阵；C为结果矩阵；α和β为常因数，取α=1，β=0.

算法实现过程中先调用CUBLASCreate函数载入CUBLAS函数库，调用CUDAMalloc函数为A，B和C开辟显存空间，并通过CUBLASSetMatrix函数将A和B输入显存空间，然后调用CUBLASSgemm函数实现矩阵相乘，计算完成后通过CUBLASGetMatrix函数将C输出到主机内存，最后通过CUDAFree函数释放显存空间，并调用CUBLASDestroy函数释放所有与CUBLAS函数库内容相关的资源.

2.2.2矩阵求逆

对非奇异矩阵A和单位矩阵B，用高斯消元方法能够将A/B转化成B/A-1.[10]从CUDA架构的编程思路出发，将算法中的指令尽量设计为少分支、可多线程并行执行模式，以便于GPU进行成块数据运算.矩阵求逆主要包括归一和消元2种操作[11]，算法描述如下.

1）在MATLAB中对矩阵A和B初始化并通过接口函数将数据输入CUDA程序中.

2）在GPU中为A和B分配显存空间，并把A和B拷贝到GPU的显存空间中.

3）调用内核函数[12]计算.

4）计算完成后，将结果从GPU显存拷贝到到主机内存中.

5）释放显存空间.

其中，内核函数的主要求解步骤如下.

1）用一组临时标量记录A中第i行的对角线元素.

另外，CUDA函数库提供矩阵求逆运算函数，可通过编写CUDA程序直接调用该函数.基于以上方法，能够实现大型矩阵在GPU下的求逆运算.

2.2.3矩阵除法

在MATLAB对GPU计算的原生支持中已经支持矩阵除法运算，因此只需通过GPUArray函数将待处理数据传入GPU内存中，然后重新加载MATLAB中的除法运算，通过Gather函数将计算结果传出到主机内存，由MATLAB执行显示结果，实现过程代码为G_A=GPUArray（A）

A和B为待除矩阵；C为结果矩阵；G_A，G_B和G_C为与A，B和C相对应的在显存空间中的数据；GPUArray为MATLAB中将数据传入显存空间的函数；Gather为与GPUArray相对应的将数据从显存空间传出到主机内存的函数.

3计算效率与误差分析

3.1GPU单精度和双精度浮点运算能力

根据浮点运算能力的计算公式，核数×主频×每个时钟周期可执行的浮点数运算次数，计算得到GTX760的单精度浮点运算能力为2.21 TFLOPS，双精度浮点运算能力为0.11 TFLOPS.[13]

双精度浮点运算能力只有单精度的1/20，因此为获得最大的加速效率，基于GPU的数据处理采用单精度数据.然而，MATLAB默认的计算数据类型为双精度类型.因此，为保证结果的准确性，在获得效率提高的同时需要分析基于GPU（单精度类型数据）的结果与基于CPU（双精度类型数据）的结果之间的误差.若误差在允许范围内，则表明基于GPU的计算结果能够用于工程计算.

3.2效率分析

通过有限元法计算双层网壳的总体刚度矩阵、等效静力风载荷，并根据式（1）求解节点位移，计算过程分别由式（2）～（4）完成.同时定义计算效率测量指标为并行加速比=串行计算时间/并行计算时间.位移计算结果见图2～4.

由表2可以看出，基于CPU的MATLAB求逆和乘法求解节点位移的耗时最长，而式（3）将求逆和乘法通过GPU实现，获得一定程度上的加速，为原来串行计算的6倍左右，最后通过改进算式，将求逆和乘法转换成矩阵除法并且通过GPU实现矩阵除法运算，获得23倍的加速比，可大大提高计算效率.CPU和GPU的硬件结构简图见图5.由此可以看出：CPU中存在大量的控制单元Control和计算单元ALU，同时还存在大块的高级缓存Cache，其中计算单元所占比例不大.这是由于CPU是串行执行模式，需要通过控制单元与快速缓存决定指令流与数据的连续处理，而GPU是单指令多线程模式，对单指令能够同时并发处理，且其中存在大量的计算单元，尽管其主频远低于CPU，但是当处理的数据量较大时，GPU的并行处理效率远远超过CPU的串行处理效率.

GPU在高性能计算中，大数据对存储容量的要求较高.本算例中使用显卡GTX760的显存容量为2 048 MB，其使用分为显示和计算2部分.在正常显示下，GPU的内存使用量约为300 MB，而通过GPU实现快速计算时，大量数据将拷贝到显存中，在计算式（3）和（4）时，显存使用量分别达到1 680 MB和1 210 MB，占用量大.因此，在进行更大规模计算时，必须考虑单块显卡的存储容量限制，当数据量过大导致无法放置于单块显卡时，需要考虑使用高性能计算显卡或多GPU节点，从而实现大数据在GPU上的处理.

3.3误差分析

以式（2）的求解结果为参照，分析式（3）和（4）得到的节点位移的相对误差E，以对数坐标表示，见图6和7.

误差分析发现，基于GPU的式（3）与式（4）求解节点位移的误差相近，式（3）的误差为4.41×10-4，式（4）的误差为4.30×10-4，均在10-4左右，因此可以认为基于GPU的节点位移求解结果与CPU计算结果基本一致，误差在允许范围内，计算结果能够满足工程精度.

4结论

以等效静力风载荷下某大跨双层柱面网壳的静力位移求解为工程背景，阐述涉及大型矩阵结构计算的GPU并行实现过程，通过分析得出以下结论.

1）基于GPU的快速并行计算能够大幅提高计算效率，尤其是对大数据量的单指令运算能够表现出明显的优势.

2）由GPU计算所得到的单精度数据结果与MATLAB计算的双精度数据结果存在一定误差，但误差较小，能够满足实际工程计算要求.

3）节点位移求解是各类结构计算中的重要部分，可能成为结构设计效率或优化分析效率的瓶颈，基于GPU的并行计算方法能够快速、准确地为后续结构分析提供有效的计算数据.参考文献：

[1]SHANE C. CUDA并行程序设计GPU编程指南[M]. 苏统华， 李东， 李松泽， 等， 译. 北京： 机械工业出版社， 2012： 1069.

[2]刘维. 实战MATLAB之并行程序设计[M]. 北京： 北京航空航天大学出版社， 2012： 10120.

[3]刘绍波， 刘明贵， 张国华. 基于CUDA的加速MATLAB计算研究[J]. 计算机应用研究， 2010， 27（6）： 21402143.

LIU Shaobo， LIU Minggui， ZHANG Guohua. Model of accelerating MATLAB computation based on CUDA[J]. Appl Res Comput， 2010， 27（6）： 21402143.

[4]张健飞， 沈德飞. 有限元GPU加速计算的实现方法[J]. 计算机辅助工程， 2014， 23（2）： 4145.

ZHANG Jianfei， SHEN Defei. Implementation method of GPUaccelerated finite element calculation[J]. Comput Aided Eng， 2014， 23（2）： 4145.

[5]叶孟洋. 大跨度干煤棚结构风载风洞试验研究[D]. 上海： 同济大学， 2006.

[6]黄友钦. 风雪共同作用下大跨度屋盖结构的动力稳定[D]. 上海： 同济大学， 2010.

[7]黄友钦， 岳启哲， 傅继阳， 等. 基于应力比法的双层网壳结构抗风优化[J]. 结构工程师， 2013， 29（4）： 112117.HUANG Youqin， YUE Qizhe， FU Jiyang， et al. Wind resistant optimization of doublelayer reticulated shells by the stress ratio method[J]. Struct Engineers， 2013， 29（4）： 112117.

[8]杨茀康， 李家宝. 结构力学[M]. 4版. 北京： 高等教育出版社， 2006： 18.

[9]王焕定， 焦兆平. 有限单元法基础[M]. 2版. 北京： 高等教育出版社， 2010： 19.

[10]李庆扬. 数值分析[M]. 5版. 北京： 清华大学出版社， 2008： 11.

[11]刘丽， 沈杰， 李洪林. 基于GPU的矩阵求逆性能测试和分析[J]. 华东理工大学学报（自然科学版）， 2010， 36（6）： 812817.

LIU Li， SHEN Jie， LI Honglin. Performance testing and analysis for matrix inversion base on GPU[J]. J East China Univ Sci & Technol（Nat Sci）， 2010， 36（6）： 812817.

[12]RYOO S， RODRIGUES C I， BAGHSORKHI S S， et al. Optimization principles and application performance evaluation of a multithreaded GPU using CUDA[C] //Proc ACM SIGPLAN Symrposium Principles & Practice Parallel Programming. New York： ACM Press， 2008： 7382.

[13]AHMED E Z， ERIC M C， ALISTAIR R， et al. Performance evaluation of the NVIDIA GeForce8800 GTX GPU for machine learning[C] //Proc 8th Int Conf Comput Sci. New York： Springer Verlag， 2009： 466475.