“求变”带给学生累累硕果

钱祥勇

[摘 要]“尝试”和“探索”是在小学数学新课程标准中“出镜率”很高的两个词语。学生只有在新的挑战面前才能做出新的思考，在不断的经历和比较中才能有所进步。而数学问题的来源有很多，可以来自于生活，也可以是原来数学模型的变型。

[关键词]变换问题 尝试 教学探索

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）26-081

很多时候，巧妙地变化一个问题能给学生带来超过问题本身的思维冲击，让学生得到更多的启发。本文结合实例从三个方面来谈谈数学问题求变的妙处。

一、变换问题难度，收获领悟

数学学习是层层深入的，如果设计的问题总是平铺直叙，前后难度一致，那么学生经受这样大量的练习只能是在技能上得到锻炼。所以在实际教学中，我们可以设计难度逐步提高、挑战性越来越强的问题让学生来尝试，使得学生在挑战中领悟数学知识的本源。

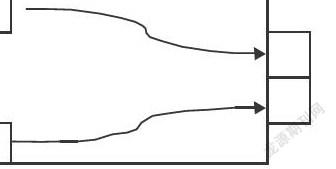
例如，六年级“长方体的体积”教学中，有这样一个问题：一张长方形铁板长60厘米、宽40厘米，从它的四个角分别剪去一个边长为10厘米的正方形，做成一个无盖的长方体容器，容器的容积是多少？（不考虑铁板厚度）在学生通过画图掌握问题的解法后，我将问题适当做了一些变化（如图），只剪去长方形的两个角，将减下来的部分拼接到长方形上，让学生来计算无盖长方体的容积。学生在读题后发现不知道剪去的正方形的边长，那么这个问题怎么解决呢？我请大家在小组中交流，集思广益。全班讨论的时候，学生从不同的规律入手，找出解题的办法：将这个新图形跟上一题的题型类比，发现做成长方体容器的图形形状还是一样的，所以右边两个正方形的上面和下面应该各有一个跟左边一样的正方形，由此可知，长方形的宽等于四个正方形的边长。

改编的这一个问题比原题容量更大，也更具有挑战性，其中融合了长方体的特点等相关知识，将学生脑海中的诸多知识点调动起来，从而加深了学生对长方体的认知。

二、变换问题角度，收获灵动

数学学习有其自身的特点，知识内化的关键在于学生的领悟度。在提出数学问题时，我们可以适当变换问题的角度，让学生有机会进行更深入的探索，并在积极探索中有所发现，久而久之，学生的思维会更灵动，数感会显著加强。

例如，在“打折问题”的教学中，有这样一个教学片断：

师：一件大衣标价600元，现在打八折出售，现价多少元？

生1：600×80%=480元。

师：使用贵宾卡还可以再打九折，现在多少元？

生2：480×90%=432元。

师：那么这件大衣实际上打几折呢？

（学生独立练习）

生3：我算出打的是七二折，600×80%×90%=432，432÷600=72%。

生5：我有更简单的做法，直接用80%×90%=72%。

生6：我补充一下，我们可以列一个综合算式600×80%×90%÷600，这样就发现实际折扣率只要用80%×90%就可以了。

……

不得不承认学生这样的发现是可贵的，显示出学生思路的灵活性。这样的发现源于变换了问题角度，让学生通过自己的研究透过了表象发现了折扣问题的实质。教学中我们可以多抛出这样的问题，让学生有机会去尝试、去发现、去收获。

三、变换问题情境，收获理念

有些时候学生在数学问题上犯错不是因为没有能力解决问题，而是因为某些“印象”影响了学生，让学生轻易做出了结论。在数学教学中，可以经常变换问题情境，让学生在事实面前发现具体问题要具体分析，以此树立“注重审题”的理念。

例如，有这样一道分数选择题：两根同样长的绳子，第一根减去了它的三分之一，第二根减去三分之一米，哪一根剪去的长？因为不知道绳子原来的长度，所以三种情况都有可能，那么这个问题的答案是无法确定的。多次遇到相似的问题，学生的思维就固化了，以后看到相似的问题，第一反应就是答案无法确定。因此，我将问题做了一点改变：一根绳子，第一次剪去它的七分之四，第二次剪去七分之四米，哪次剪去的长？大部分学生给出的答案都是“无法确定”。只有少数同学发现了其中的蹊跷：现在是一根绳子，不是两根绳子了，第一次剪去绳子的七分之四，这个分数已经超过一半了，所以第二次再怎么剪，这个七分之四米都不会有绳子的七分之四那么长。这样的问题有警示作用，同时传达给学生一个理念：审题是必不可少的。

“数学是聪明人的思维游戏”，那么在这个游戏中我们不妨多一些变化，让学生的学习多一些层次。数学教学中教者应当积极求变，让学生在变化中得到必要的发展，上升其认知，深化其所得，获得累累硕果。

（责编 罗 艳）