基于统计量模式分析的T-KPLS间歇过程故障监控

常鹏，王普，高学金



基于统计量模式分析的T-KPLS间歇过程故障监控

常鹏，王普，高学金

（北京工业大学电子信息与控制工程学院，北京 100124）

核函数的全影结构投影(total kernel projection to latent structures,T-KPLS)最近在故障监控领域取得了广泛应用，其实质是对数据矩阵的协方差矩阵进行分解，没有利用数据的高阶统计量等有用信息，在进行特征提取时会造成数据有用信息的丢失，导致故障识别效果差。为了解决此问题，提出了统计量模式分析(statistics pattern analysis, SPA)与核函数的全影结构投影法(total kernel projection to latent structures, T-KPLS)相结合的多向统计量模式分析的核函数的全影结构投影法(multi-way statistics pattern analysis total kernel projection to latent structures, MSPAT-KPLS)。该方法首先构造样本的不同阶次统计量, 将数据从原始的数据空间映射到统计量样本空间，然后利用核函数将统计量样本空间映射到高维核空间并在质量变量的引导下将特征空间分为过程变量与质量变量相关、过程变量与质量变量无关、过程变量与质量变量正交和残差4个子空间；最后针对与质量变量相关和残差空间建立联合监控模型，当监控到有故障发生时进行故障变量追溯。最后将该方法应用到微生物发酵过程中，并与传统方法进行比较，发现该方法具有更好的监控性能。

故障监控；核函数全影结构投影；统计量模式分析

引 言

多向偏最小二乘(MPLS)方法利用输入对输出的解释作为特征提取的依据，提取较少的主元去更好地解释与质量相关的信息，非常适合检测与质量相关的故障，近年来在间歇生产过程故障监测方面取得了广泛应用[1-6]，但是深入研究后发现经MPLS分解后的主元空间含有与质量无关的成分，在构建监控模型时应该去除。为此Li等[7-9]提出了质量相关的T-PLS(total PLS)方法，他们将MPLS分解后的主元空间和残差空间用主成分分析(PCA)[10-11]分解成与质量相关、与质量无关、与质量正交和残差4个子空间并分别构建监控模型，克服输入过程变量与输出质量相关故障检测方法的不足，但是以上方法的本质是线性化建模，面对复杂的非线性系统，如生物发酵过程，变量间往往存在较强的非线性关系，利用传统的线性方法将会给过程监控带来较大的误差。为了解决该问题，T-PLS方法被推广到非线性领域，Peng等[12]将核函数引入T-PLS中，提出了全影核偏最小二乘(totoal kernel partial least squares, KPLS)方法，T-KPLS的基本思想是将原输入空间线性不可分的数据通过核函数映射到高维特征空间变为线性可分，然后再把高维空间分为与质量相关、与质量无关、与质量正交和残差4个子空间并建立与质量相关和残差的联合统计模型，进一步提高了与质量相关故障的监控性能。

然而以上方法仅仅利用了数据的二阶协方差信息，未考虑数据的高阶统计量信息造成对数据信息提取的不完整，在监控过程故障时会引起较大的误警率，甚至失去监控性能[7-9]。统计量模式分析(statistics pattern analysis， SPA）)是由He等[13-14]提出的将高阶统计量信息用于数据建模的数据分析技术，近两年Zhang等[15]和常鹏等[16]将统计量模式分析(SPA)应用在过程监控领域并取得了不错的效果。但是高阶统计量的引入并未解决数据本身的非线性，而相同变量的不同统计量之间会引入新的非线性关系，增加了原始样本的非线性，在监控非线性系统时监控效果不好，本文将统计量模式分析引入T-KPLS中，多向统计量模式分析的核函数的全影结构投影法(multi-way statistics pattern analysis total kernel projection to latent structures, MSPAT- KPLS)。其核心算法由以下3部分构成：① 将三维数据按照AT方法展开为二维数据然后构造样本不同阶次的统计量将数据从原始的数据空间映射到统计量样本空间；②利用核函数将统计量样本空间映射到高维核空间解决变量间的非线性关系，并将高维核空间分为4个子空间并分别构造监控模型的统计量；③将质量相关子空间的统计量与残差子空间的统计量相结合构造新的统计量用于与质量相关的过程故障监控，当监控到有故障发生时，引入Peng等[12]提出的故障诊断方法用于故障变量的追溯。最后将本文方法应用在Benchmark模型[17]和实际工厂并与T-PLS、T-KPLS方法进行比较，验证该方法的有效性。

1 基于SPA的样本空间构建

1.1 间歇过程数据的预处理

间歇过程体现为重复性生产过程，其数据集合比连续过程数据集合多一维“批次”元素，三维数据矩阵(××)(××)代表间歇过程的数据集合，其中为批量数，为变量数，为质量变量数，为采样点数。按照AT方法[18]将三维数据矩阵展开为二维数据矩阵(×)和(×)，采用该方法建模时不要求批次长度完全相等，且用于在线监控时，无需对新批次的未来测量值进行估计。AT 展开方法如图1所示。

1.2 统计量样本空间的构建

计算数据矩阵(×)不同的统计量，将所有选择的统计量排列在一个行向量中如式(1)所示

其中，表示变量的均值是一阶统计量

表示样本的方差是二阶统计量

表示样本的偏度是三阶统计量

表示样本的跨度是四阶统计量

由式(4)和式(5)可以看出高阶统计量的引入加大了统计量样本之间的非线性，传统的线性建模方法在此不再适用，固本文引入核来解决统计量样本之间的非线性。

2 监控模型的构建及在线监控

2.1 监控模型的构建

MSPAT-KPLS的目标是首先通过构造不同样本统计量in，然后利用核函数将统计量样本空间映射到高维核空间解决变量间的非线性关系，并将高维核空间分为4个子空间并分别建立监控模型。将输入变量in映射到高维空间，由于特征空间的维数很高甚至无穷维，其内积计算量非常大，利用核技巧可以避免内积运算，其核矩阵K的计算如

（1）将三维数据矩阵按照AT方法展开为二维数据矩阵并按照式(1)构建样本统计量然后初始化，其中=1，=in，=。

（3）求输出变量的负载：=Tt，单位化向量

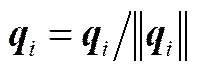
（4）计算得分向量

（5）重复步骤（2）～步骤（5），直至收敛转步骤（6），否则，回到步骤（3）。

（6）计算下一时刻in,i+1和+1

+1=(8)

（7）令=+1，如果>则终止循环，否则回到步骤(2)，主元个数由交叉验证法确定，最终将数据块in和分解为如下，具体步骤可参阅文献[10]

=q+(10)

其中，是原始得分矩阵和直接相关的部分；是原始得分矩阵中和正交的部分；是原始残差中方差变化较大的部分；而则是in的最终残差，代表噪声。

2.2 监控统计量及其控制限的构建

对于核矩阵in，其相应的得分向量和残差如下[10]

2，2和2的控制限可以利用分布来计算，而Q统计量可以用2分布来计算，故障检测所需统计量及其相应控制限计算方法算如表1所示，其中，，，1,n1,a代表自由度为1和-1, 置信度为的分布，=/2，=2/，是样本的均值，是样本的方差，是一个尺度因子为、自由度为、置信度为的2分布的临界值。构建和的联合统计量

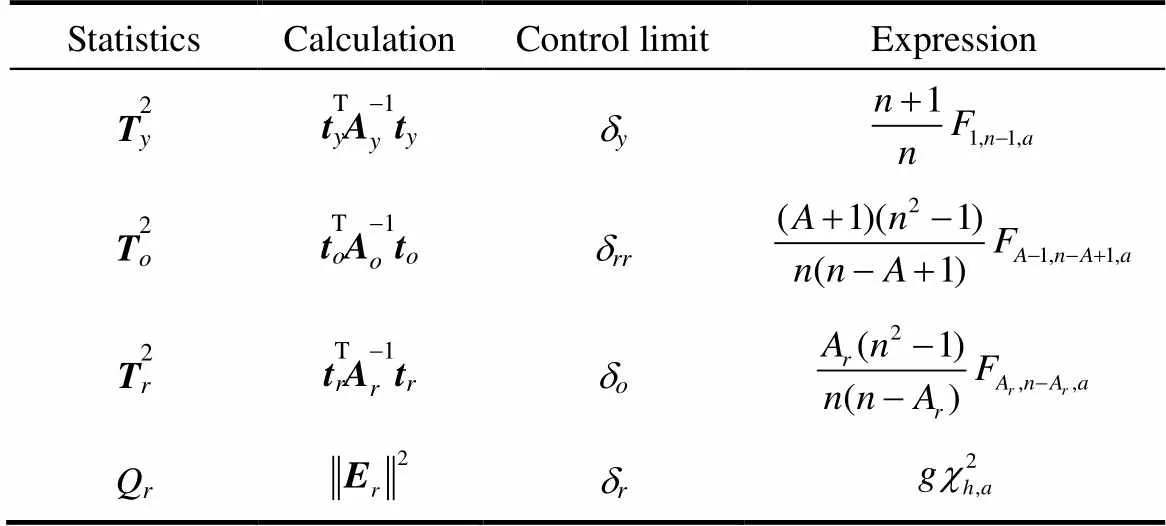
表1 监控统计量和控制限 Table 1 Monitoring statistic and control limit

如下

由公式可知，改进后的监控统计量可以更好地监控与质量相关的故障，统计量计算的具体推导过程参见文献[12]。

2.3 在线监测

（1）对于新得到的在线数据按照2.1节和2.2节的方法进行处理得到的数据new,t∈R,=1,…,N；然后计算核矩阵∈1×N

new,t=new,t-K-new,t+K1(17)

（2）计算新时刻的统计量，并判断其是否超过控制限，若未超限，说明系统运行在正常工况下；若超限，说明系统发生故障，对其进行故障诊断。

2.4 故障诊断

近年来Alcala等[19-20]提出了故障重构的方法应用在非线性系统的故障诊断，并取得了不错的效果，然而基于故障重构的技术需要大量的已知故障，而实际的间歇过程缺乏故障数据。而由Peng等[12]提出的基于核函数故障诊断方法应用在非线性的故障诊断并取得了很好的效果，但是以上方法是在连续过程上的应用，为此本文将其扩展到间歇过程领域的用于故障变量的追溯。

3 算法仿真验证

3.1 算法仿真应用

本文选用美国Illinois州立理工学院的青霉素仿真平台[16]。青霉素发酵每个批次的反应时间为400 h，采样间隔为1 h，选取10个过程变量和2个质量变量进行监测，如表2所示。为了验证本文算法的有效性，本文共生产了40个正常批次数据作为模型的训练样本并与T-PLS和T-KPLS算法进行比较，主元个数和核参数选择如表3所示，故障类型如表4所示，由于篇幅的限制本文只给出故障1的效果图，其他的监控结果见表5。图3、图４、图5分别为采用T-PLS、T-KPLS和本文算法对故障1的监控结果。由图3可以看出，其在监控过程中存在较大的漏报，漏报率为82.7%，这是因为过程中存在大量的非线性[16]，T-PLS对非线性过程监控效果差。图4为T-KPLS方法，其能较好地处理非线性过程，监测效果优于T-PLS方法，但是由于其仅仅关注二阶协方差信息，忽略了数据的高阶信息，造

表2 模型所用变量 Table 2 Variables used in the model

表4 仿真中用到的故障类型 Table 4 Fault types introduced in process

成故障报警的延迟，漏报率为10.6%，图5为本文方法对故障批次的监控结果，漏报率为3.2%，优于上述方法，这是因为引入高阶统计量后其对数据有用信息的提取更加完整，弥补了传统方法的不足，如表4可知，本文方法的监控性能优于传统方法。

3.2 故障诊断

针对故障按照2.4节的方法进行故障变量追溯，在这里只给出故障1的故障诊断图（图6），其他见表6，可以看出该故障诊断方法可以准确识别故障源。

表6 时刻贡献图识别故障 Table 6 Moment contribution figure to identify fault

4 算法工业实际应用

将本文算法应用在北京某生物制药有限公司的制药过程监控，本小节实验的核参数选为4.2，主元个数选为4，建模用的变量如表7所示。实际故障批次1：由搅拌速率引起的故障，类型为阶跃故障，引入时间15 h到发酵结束，大小为20%。实际故障批次2：由搅拌速率引起的故障，类型为斜坡故障，引入时间15 h到发酵结束，大小为斜率-0.2%的斜坡故障。

图7和图9是分别针对故障1和故障2的监控图，结果表明MSPAT-KPLS方法可以及时、准确监

表7 过程变量与质量变量 Table 7 Process variables and quality variables

测到故障，图8和图10分别为实际故障1和实际故障2诊断图，结果表明该方法可以准确识别出故障源。

5 结 论

传统T-KPLS方法未利用数据的高阶统计量等有用信息，在进行特征提取时会造成数据有用信息的丢失，导致故障识别效果差，为了解决此问题，引入SPA技术，提出MSPAT-KPLS。该方法首先通过构造样本的不同阶次统计量将数据从原始的数据空间映射到统计量样本空间，然后利用核函数将统计量样本空间映射到高维核空间并在质量变量的引导下将特征空间分为过程变量与质量变量相关、过程变量与质量变量无关、过程变量与质量变量正交和残差4个子空间；最后针对过程变量与质量变量相关和残差2个子空间建立联合监控模型用于过程监控，当监控到有故障发生时引入时刻贡献图方法用于故障变量的追溯。将该方法应用到工业过程中，发现该方法具有更好的监控性能，并能够及时准确识别出故障源。

References

[1] Mori J C, Yu J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach [J]., 2014, 24(1): 57-71

[2] Xiong H S, Gong X C, Qu H B. Monitoring batch to batch reproducibility of liquid-liquid extraction process using in-line near-infrared spectroscopy combined with multivariate analysis [J]., 2012, 70(11): 178-187

[3] Jia Runda (贾润达), Mao Zhizhong (毛志忠), Wang Fuli (王福利). KPLS model based product quality control for batch processes [J].( 化工学报), 2013, 64(4): 1332-1339

[4] Stubbs S, Zhang J, Morris J L. Multiway interval partial least squares for batch process performance monitoring [J].，2014, 52 (35) : 12399-12407.

[5] Geert G, Jef V, Jan F. Discriminating between critical and noncritical disturbances in (bio)chemical bach processes using multi-model fault detection and end-quality prediction [J]., 2012, 51(1): 12375-1238

[6] Naes T, Tomic O. Multi-block regression based on combination so for thogonalisation, PLS regressionand canonical correlation analysis [J]., 2013, 124: 32-42

[7] Li G, Alcala C F, Qin S J,. Output relevant fault reconstruction and fault subspace extraction in total projection to latent structures models [J]., 2010, 49(19):9175- 9183

[8] Zhou D, Li G, Qin S J. Total projection to latent structures for process monitoring [J]., 2010, 56(1): 168-178

[9] Li G, Alcala C F, Qin S J,. Generalized reconstruction based contributions for output relevant fault diagnosis with application to the Tennessee Eastman process [J]., 2011, 19(5): 1114-1127

[10] Jackson J E. A User’s Guide to Principal Components[M]. New York: Wiley, 1991

[11] Nomikos P, MacGregor J F. Monitoring batch process using multiway principal component analysis [J]., 1994, 40(8): 1361-1375

[12] Peng K X, Zhang K, Li G,. Contribution rate plot for nonlinear quality related fault diagnosis with application to the hot strip mill process [J]., 2013, 21(4): 360-369

[13] He Q, Wang J. Statistics pattern analysis: a new process monitoring framework and its application to semiconductor batch processes [J]., 2011, 57(1): 107-121

[14] Wang J, He Q. Multivariate statistical process monitoring based on statistics pattern analysis [J]., 2010, 49(1): 7858-7869

[15] Zhang Hanyuan(张汉元), Tian Xuemin(田学民), Deng Xiaogang(邓晓刚). Fault identification method based on SPA similarity factor [J].(化工学报), 2013, 64(12): 4503-4508

[16] Chang Peng(常鹏),Wang Pu(王普),Gao Xuejin(高学金),. Batch process monitroing and quality prediction based on statistics pattern analysis and MKPLS [J].(仪器仪表学报), 2014, 35(6): 1409-1416

[17] Birol G, Undey C, Cinar A. A modular simulation package for fed-batch fermentation: penicillin production [J]., 2002, 26(11): 1553-1565

[18] Agudo D, Ferrer A, Ferrer J,. Multivariate SPC of a sequencing batch reactor for wastewater treatment [J]., 2007, 85(1): 82-93

[19] Alcala C F, Qin S J. Analysis and generalization of fault diagnosis methods for process monitoring [J]., 2011, 21(1): 322-330

[20] Alcala C F, Qin S J. Reconstruction based contribution for process monitoring [J]., 2009, 45(1): 1593-1600

Fault monitoring batch process based on statistics pattern analysis of T-KPLS

CHANG Peng, WANG Pu, GAO Xuejin

(College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China)

Total kernel projection to latent structures (T-KPLS) has been widely used in the fault detection control field, its core idea is to conduct the covariance matrix decomposition of the data matrix, without using the higher-order statistics and other useful information of the data, which will cause an information loss in the feature extraction process, then result in a bad fault recognition performance. Aiming to solve the problem, a statistics pattern analysis (SPA) combing with the T-KPLS based multi-way statistics pattern analysis total kernel projection to latent structures (MSPAT-KPLS) is proposed. First, different order statistics of the data samples are constructed to map the data from the original data space into the statistic sample space, then utilize kernel function to map the statistic sample space into the higher dimensional kernel space, and according to the quality variable, the feature space will be divided into 4 subspaces, namely: process variable related to quality variable space, process variable not related to quality variable space, process variable orthogonal to quality variable space and residual error space; Lastly, aiming at the process variable related to quality variable subspace and the residual error space, different detection models are constructed, which will trace the fault variables when faults are detected. In the end, apply the proposed method on the microbial fermentation process, and the comparison results with the traditional methods show that the proposed method could achieve a better detection.

fault monitoring; total kernel projection to latent structrues; statistics pattern analysis

date: 2014-09-28.

CHANG Peng, changpeng2011@emails.bjut. edu.cn

10.11949/j.issn.0438-1157.20141476

TP 273

A

0438—1157（2015）01—0265—07

国家自然科学基金项目(61174109,61364009)。

2014-09-28收到初稿，2014-10-09收到修改稿。

联系人及第一作者：常鹏（1981—），男，博士研究生。

Foundation item: supported by the National Natural Science Foundation of China (61174109,61364009)