关于健全评价标准的思考

姚春艳 张勇

2013年教育部《关于推进中小学教育质量综合评价改革的意见》（以下简称《意见》）中明确了若干个需要完成的实验任务，“健全评价标准”是其中之一。所谓评价标准，是指在评价活动中应用于对象的价值尺度和界限，是对评价结果做出有意义解释的依据。如何健全中小学教育质量综合评价标准呢？

根据评价指标的特点，确定指标适合绝对评价还是相对评价

以评价标准分类，教育评价可以分为绝对评价和相对评价两大类。绝对评价（absolute evaluation）是指在评价对象的群体之外，以预先制定的目标为评价基准，把评价对象与之比较，确定评价对象达到目标基准绝对位置的评价。相对评价（relative evaluation）是在被评价对象的集合中选取一个或若干个作为基准，然后把各个评价对象与基准进行比较，从而评出其在团体中的相对位置的评价。绝对评价的优点是：为评价对象提出了明确的努力方向和应达到的目标，有利于引导评价对象克服盲目性，增强自觉性，排除干扰，从而提高工作、学习效益；在准确的评价之后，每个被评者可以明确自己的实际水平及与客观标准的差距，有利于创设一种积极向上的氛围。绝对评价的缺点则表现为：评价标准的制定对人员的专业性要求极高；评价对象由于欠缺横向比较容易产生自我满足，不利于形成竞争氛围。

相对评价的优点有：适应性强，应用面广，不管团体状况如何，都可以进行比较，都能评出个体在集体中的相对位置；用建立在对评价对象群体测评基础之上的标准进行评价，可以发现其个别差异，从而对被评个体做出较为客观、公正和确切的判断；有利于激发评价对象的竞争意识。相对评价的局限性在于：因缺乏外在的客观标准，评选出来的优秀者未必就是真正的高水平、高质量者，未被选上的也不一定水平低、质量差，故容易降低客观标准；评价的结果所反映的只是评价对象在一定范围内的相对位置，不一定反映他们的实际水平；易忽视教育目标的完成情况；易导致激烈的、无休止的竞争，从而挫伤一部分人的积极性。

由于绝对评价与相对评价各有利弊，因此，自20世纪80年代以来，将绝对评价与相对评价结合在一起，使双方形成相容的互补关系的思想，代表了教育评价理论的发展趋势。目前，美国和日本等国家采取绝对评价和相对评价并用的办法。

中小学教育质量综合评价改革给出了20项关键指标，有些指标是可以建立明确的客观标准的，如学业发展水平中的知识技能以及学科思想方法。由于国家已经颁布了学科课程标准，对各个学科的学生在不同的学段应该掌握的知识、技能以及学科思想方法做出了较为明确的规定，因此可以采用绝对评价。而另外一些指标，如兴趣特长养成中的潜能发展，则只适宜采用相对评价。因此，若要为中小学教育质量综合评价改革各指标健全评价标准，需要先明确各个指标适用的评价标准。

查考各种相关文件，为适合绝对评价的指标建立客观评价标准

依据绝对评价的定义可知，绝对评价是在被评价对象之外，存在一个预先制定的评价标准，这种标准是不依赖于被评价对象的客观标准。客观标准的制定，必然要参考已有的规定、要求、标准等。2013年《意见》文件附带的《中小学教育质量综合评价指标框架（试行）》（以下简称《指标框架》）给出了各评价指标的主要评价依据。相关人员需要做的，就是查考这些文件，将散落在各个文件中的、与同一指标有关的要求整合在一起，即可形成某一指标的客观评价标准。下表中给出的是2013年《指标框架》中适宜采用绝对评价、可以健全客观标准的评价指标以及建立客观标准可以参考的依据。

以统计学知识与方法为依据，为适合采用相对评价的指标建立相对评价标准

对于那些仅适合相对评价的指标，需要通过一定的方法，在评价对象群体中确立一些基准，即相对评价的标准，使得各个评价对象可以与之相比较，进而获得关于被评价个体的认识和理解。现代统计学知识及方法在设立这类相对评价标准方面可以提供非常有益的帮助。一般而言，同时采用反映数据集中趋势和离散趋势的两类统计指标，能更有效地帮助数据使用者做出判断。

传统评价中，应用最为广泛的，用于反映数据集中趋势的统计量是平均分。但平均分在代表一组数据的集中趋势时，容易受到极端值影响，从而使其对总体的代表性降低。因此，为了更为客观地反映一组数据的集中趋势，可以在平均数（分）基础上，引入中位数（分）。中位数不受数列的极大或极小值影响，从而在一定程度上提高了数列分布的代表性。和平均数（分）相比，中位数（分）在反映数据集中趋势时的优势可以从表2的例子中看出。

从上表中可以看出，虽然A学校和B学校的平均成绩相同，但B学校的中位分却显示，B学校有50%的学生的成绩高于69.5分，而A学校50%的学生的成绩只是高于68.06分。使得两所学校的平均分相等的原因在于，同B学校相比，A学校中存在极高值（100）和极低值（10），因此，虽然两所学校的平均分相同，但B学校的平均分的代表性要优于A学校。如果没有中位分作为参考，仅从平均分来判断，我们会得出A学校和B学校情况差不多的结论。引入中位分，就会使评价结果的可解释性进一步增强。

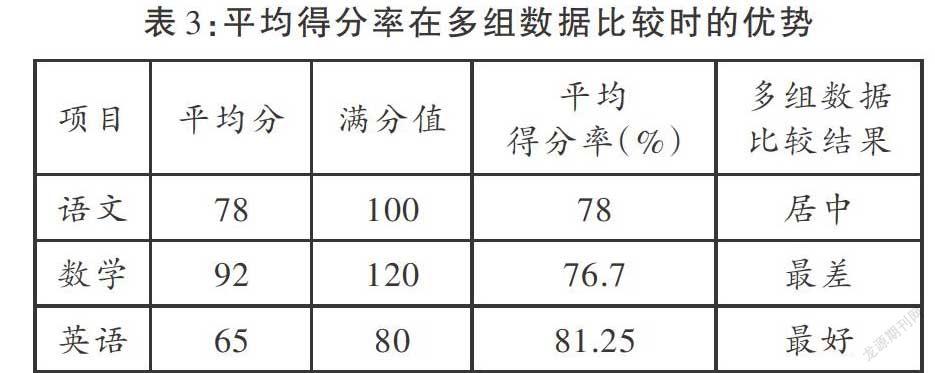
在教育评价中，我们经常会遇到需要进行多组数据之间的比较，如一个班级的语文、数学、英语三科同时比较，希望获得学生在哪一个学科上表现更好的信息。如果每一科的满分都是100分，则使用平均分进行比较可以获得一定的信息。然而，当每科的满分不同时，采用平均分将无法比较。此时需要引入平均得分率（比值），比较才有意义。表3是一个关于平均得分率在多组数据比较中的优势的例子。

在教育评价中，除了用反映集中趋势的统计指标了解学生群体的整体特征外，有时也需要了解数据的离散情况，即每个数据偏离指定的基准的程度。平均数相同的两组数据其离散程度完全有可能不同。如果一组数据的分布比较集中，差异较小，则平均数的代表性较好，如表2中的B学校的学生成绩；若另一组数据比较分散，差异较大，则平均数的代表性就较差，如表2中的A学校的学生成绩。一组数据或成绩的离散情况反映的是被评价对象之间的均衡性，离散程度越高，表明均衡性越差，反之，则均衡性越好。良好的教育质量，应该是在平均分高的同时，学生的均衡性也较好。因此反映数据离散趋势的统计指标应该成为相对评价的另外一个标准。

以往教育评价中常用的反映数据离散趋势的统计指标是标准差。然而，标准差只能度量一组数据对其均值的偏离程度。若要比较两组以上数据的离散程度，用两个标准差直接进行比较有时就显得不合适了。在这种情况下，可以引入另外一个统计量：变异系数。变异系数的公式为：SD/MN*100，其中SD为每组数据的标准差，MN为每组数据的平均值。变异系数使得不同数据组的离散程度变得可比，用在学校教育质量评价中，能够更有效地发现不同学校之间的差异。

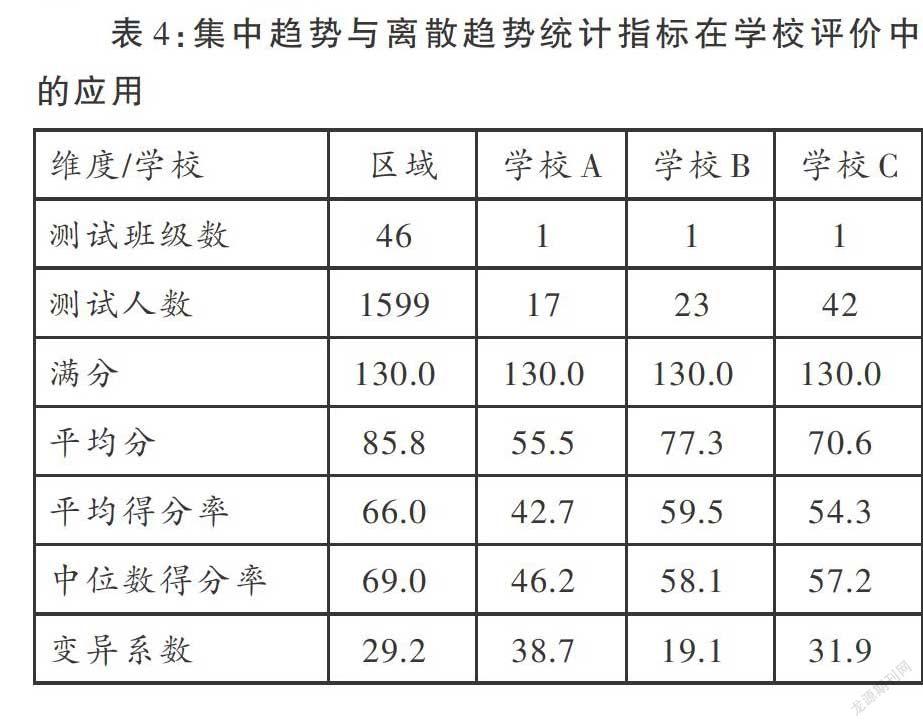
表4、5是关于集中趋势与离散趋势统计数据在教育评价中的应用案例。

从表4中可以看出，学校B是三所学校中不仅平均成绩最高，同时学生成绩的均衡性也是相对较好的一所学校，而学校A不仅平均成绩最低，且学生成绩的均衡性也是较差的一个，是需要我们重点关注的学校；而学校C，虽然平均成绩处于中等，但学生成绩的均衡性也相对较差。各个学校的特点通过这些数据表现得更为清晰，学校后期改进的方向也会更为明确。

而从表5中则可以看出，在这次测试中，“四则运算”是学生掌握较好，同时成绩的均衡性也相对较高的一个知识点，而“单名数复名数的互换”则是学生掌握相对较差，且学生间的均衡性也较差的一个知识点，但由于中位数得分率为100，表明有一半学生是已经完全掌握了该知识点的，而导致平均成绩低的原因，必然是后50%的学生中存在极低值，不仅影响了平均分，也使成绩的均衡性受到较大影响。通过分析这些数据，学校后续教学中应关注的学生群体以及关注的重点就非常清楚了。

通过上述两个应用案例可知，恰当地设定相对评价的标准，将有助于更为精准地诊断学校、教学中存在的各类问题。