解决波动问题其实并不难

何晓立

摘 要： 只要抓住波动特点，理解基本知识点，运用基本方法，就能轻松解决相关问题.文章对此展开分析.

关键词： 波的图像 解题 波动问题

“波的图像”习题，是中学物理中较难解决的问题.教师在教学过程中也各自总结了许多行之有效的方法，笔者也在教学实践中发现，只要抓住波动问题的关键知识点，深刻认识波动的规律，结合简单的方法，就能迅速准确地解决相关问题.

1.基本知识点：波的传播方向上某一质点的振动方向的判断

抓住波的形成和传播中质点“依次带动”的基本原理，先明确波的传播方向，找出“前面”的相邻质点，如图1，若波沿x轴正向传播，则P点前面的质点Q点在上方，所以带动P點向上振动.

图1

2.基本方法：已知t时刻的波形曲线，判断经过一段时间△t以后波形曲线的方法

波的图像以静止的图形反映变化的波动的规律，首先要让学生通过对波动演示箱的观察，认识到一段时间△t后的波形，其实就是t时刻波形曲线沿波的传播方向上平移v△t的距离时的波形.如果△t=T/4，则相应移动λ/4的距离.

例1：如图2所示，波沿x轴正方向传播，波速为2cm/s.某一时刻波恰好传到O点，那么经？摇 ？摇？摇？摇s，坐标为45.5cm的P点第一次到达正的最大位移.

图2

分析：波传播到P点时，P点由平衡位置开始向下振动，所以第一次到达正的最大位移还要再经过3T/4的时间.这个题还有一个解法，抓住波形平移的想法，P点第一次到达正的最大位移，其实就是第一个波峰传到P点，这样计算更加简单，答案为23.5s.

3.多解问题的产生及解决方法

多解问题的产生，一个原因是由波的传播方向不确定引起的，另一个原因是经nT时间，波形平移nλ距离，和原来的波形重合，不能分辨而产生多解.如果题设条件中没有说明波的传播方向，就可能因为第一种原因引起多解，这在阅读题目时要特别注意.

图3

例2：如图3所示，一列沿x轴方向传播的横波，t=0时刻的波形用实线表示，经△t=0.2s时的波形用虚线表示，则下列说法中正确的是（？摇？摇）

A.若波向右传播，则最大周期是1s

B.若波向左传播，则最小周期是4.5s

C.若波向左传播，则最小波速是9m/s

D.若波速是19m/s，则波向右传播

分析：本题中引起多解的两个因素是同时存在的.分析时先考虑向某一个方向传播时一个波长以内的情况.波若向右传播，一个波长以内传播了0.2m.则可能传播的距离为s■=nλ+0.2m，（n=0、1、2、…），波速为v■=■=10n+1m/s，所以有最小的波速1m/s；T=■，由图可知λ=2.0m，则有最大周期2s.

同理，波若向左传播，在一个波长以内传播了1.8m，则可能的传播距离为s■=nλ+1.8m，（n=0、1、2…），v■=■=10n+9m/s，有最小的波速9m/s，C选项正确.有最大周期2/9s，最小频率4.5H■，由以上分析可知，当波向左传播时，可能的波速有19m/s.

4.与振动结合的问题

波的图像问题还经常结合振动图像问题.振动和波动都是周期性的运动，振动是运动形式在时间上的重复，波动是运动形式在空间上的重复.波的图像反映的是某一时刻各质点的振动情况，而振动图像反映的是一个质点在不同时刻的位移。所以解决振动图像和波的图像结合的问题，一般要在某个共同的时刻，把两个图像联系起来，这个时刻，一般可以选择波的图像对应的那个时刻.

例3：一列简谐波沿x轴方向传播，已知x轴上x■=0和x■=1m两个质点的振动图像分别如图4中a、b所示，则此波的传播速度为多少？

图4

分析：这一例题中，有一个比较典型的条件，就是两点间距离已知，但要看到两点间的位置关系不确定这一点，这是这个问题的关键点.解决办法是先画出某一时刻（比如t=0时刻）的波形曲线，然后按照题目的要求，确定符合条件的两个点的位置.这是处理这类问题的一个有效方法.

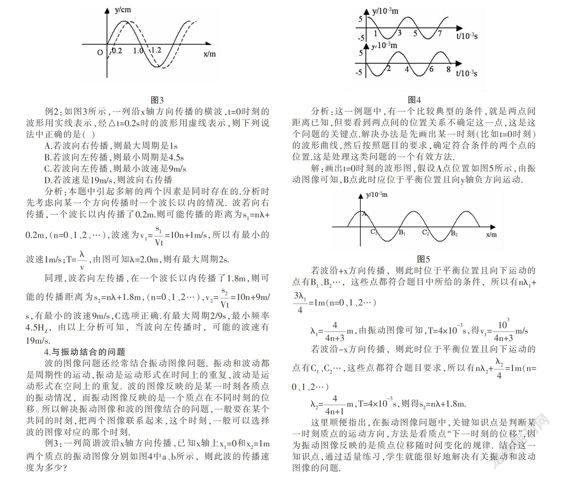
解：画出t=0时刻的波形图，假设A点位置如图5所示，由振动图像可知，B点此时应位于平衡位置且向y轴负方向运动.

图5

若波沿+x方向传播，则此时位于平衡位置且向下运动的点有B■、B■…，这些点都符合题目中所给的条件，所以有nλ■+■=1m（n=0、1、2…）

λ■=■m，由振动图像可知，T=4×10■s，得v■=■m/s

若波沿-x方向传播，则此时位于平衡位置且向下运动的点有C■、C■…，这些点都符合题目要求，所以有nλ■+■=1m（n=0、1、2…）

λ■=■m，T=4×10■s，则得s■=nλ+1.8m.

这里顺便指出，在振动图像问题中，关键知识点是判断某一时刻质点的运动方向，方法是看质点“下一时刻的位移”，因为振动图像反映的是质点位移随时间变化的规律.结合这一知识点，通过适量练习，学生就能很好地解决有关振动和波动图像的问题.