建构模型 渗透思想

祁顺成

【教学内容】

苏教版小学数学教材第十册第1～2页例题1、2及相应的练习。

【教学目标】

1.在具体的情境中，感知等式、方程、不等式等意义，明白方程和等式两个概念的关系，进而理解与掌握方程的意义。经历从真实的情境到方程概念的建构过程，感知到方程是刻画现实世界的数学模型，逐步渗透方程思想。

2.培养观察、比较、思考分析问题等方面的能力，提高学生思维的灵活性。

3.加强数学知识与生活联系的引导，着力培养学生的数学应用意识，增强学习兴趣。

【教学重点】

理解与掌握等式的构成，领悟方程的意义。

【教学难点】

帮助学生建构“方程”的模型，渗透方程思想。

【教学过程】

一、回顾，感知平衡

师：大家还记得幼儿园时的生活吗？老师收集了一组幼儿园小朋友活动的图片，一起来欣赏一下吧！（课件展示：小朋友们各种游戏活动的图片）

师：画面中玩什么的人最多啊？

生：玩跷跷板的多。有的两个人，有的四个人，还有的三个人……

师：噢！这么多的玩法啊！那你发现了什么？

生：有的两边平的，有的一边高一边低……

师：跷跷板这么有趣，谁想和老师玩一次？

师：你重多少千克？

生：28千克。

师：老师重80千克，请大家想一想，老师和他坐上跷跷板两端的时候会怎样呢？

生：一定是同学那边跷起来，老师这边沉下来。

师：我们都不动，那怎样才能使跷跷板平衡呢？你能用一个式子来说说吗？

生：再派两个同学过去，体重加起来是52千克，28+52=80（千克）。

师：不错，生活中也有类似的现象，你看见过吗？说给大伙听听。

学生自然地说出——天平。

（设计说明：基于学生的生活经验，并以此为突破口，让学生在回忆中感受平衡的存在，在观察画面中体会平衡的本义，再在师生互动中把握平衡的数学原理。这样的设计一方面立足于学生的生活经验，让学生在兴趣高涨的状态下去看、去想、去议，从而拓展视野，利于平衡、等式的连接，让数学学习变得有趣，也让数学充满生活气息;另一方面能有效地唤醒学生的学习潜能，促进知识技能、经验等的激活，诱使学生去反思活动，梳理经验与生活的关联性，为后续深入解读“平衡”提供最基本的架构。）

二、实践，领悟平衡

（一）活动，感受平衡

师：天平有这样的现象吗？那就试试看。

学生活动，小组中进行天平的操作。

师：通过活动，你感觉到了什么？

生：天平两边的重量不同时，天平是歪的;两边的重量相等时是平的。

师：很棒！天平有时是平衡的，有时是不平衡的。天平平衡了，你会用式子表示出来吗？

学生展示自己小组的活动，汇报写出的式子：10克+10克=20克，20克+30克=50克……

（二）辨析，明晰平衡

师：你认为这些式子写得对吗？它们都有什么共同点呢？

学生再度解读式子，发现这些式子都有“等于号”;式子左右两边计算的结果是相等的……

师：能用同样的策略写出那些左、右不相等的式子吗？

学生小组合作，尝试写出不等式……

（设计说明：以活动为媒，促进数学学习与数学活动的有机融合。一方面引导学生进行保持天平平衡的活动，并通过观察写出相等的式子，不仅能丰富学生的感知，更能促进平衡与等式关系的理解，而且还能诱发学习思考，促使学生去思考：天平平衡意味着什么？这些式子表示的意义又是什么等，从而让活动与思考有机地连接在一起。另一方面引导学生观察天平不平衡的例子，尝试用式子表现出来，这个过程就是锤炼思维的过程，让学生明白式子有的左、右两边是相等的，有的左、右两边是不相等的，进而强化等式的建构，帮助学生形成天平平衡与等式之间的必然联系，形成扎实的学习记忆。活动丰富了学习感知，更促进学习思维的跟进，更利于认知表象的积累，促进等式等知识的科学建构。）

三、探究，理解方程

（一）借助天平，感受未知数的存在

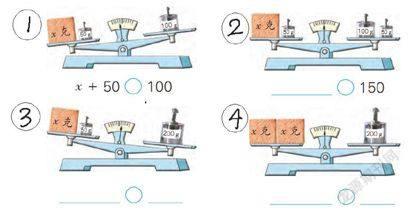
师：老师这里也有一组天平图，你能根据前面的学习写出相应的式子吗？课件出示：

学生依据图例，写出对应的式子。①x+50﹥100，②x+50=100，③x+50﹤200，④x+x=200（或2x=200）。

师：请说出自己写这些式子的想法，好吗？

学生交流自己写这些式子的理由。

（设计说明：再度借助天平图，让学生在熟悉的情境中体会到新的气息。同时，利用4组天平图有效地拓展了原有的学习认知面，为提炼未知数、方程提供孕伏，丰富学习感知。再引导学生解读天平平衡、不平衡所对应的式子，让未知数、等式等概念得到深化。）

（二）比较式子，感知方程的存在

师：我们又写出了一组关于天平的式子，请仔细比较一下前后两组式子，说说你的新发现。

学生观察前后两组式子，交流自己的理解。

生：前面的式子都是数据构成的，后面这4个中都有字母x。

生：前面的每一个都是具体的数，而后面的4个中都有不知道的。

生：老师我知道，这里的x叫作未知数。

……

师：新说法——“未知数”。你们知道吗？查查资料或小组中交流一番，看看什么是未知数。

学生活动，有的查阅资料，有的议论交流。

师：这4个式子都有未知数，它们都是一样的吗？

生：不一样，①、③用的是大于号和小于号，而②、④是等于号。

生：①、③叫不等式，②、④叫作等式。

师：很棒的解释。还有其他认识吗？

生：②、④还叫作方程。

师：是的，像这样有未知数的等式，它们是方程。

（三）解读式子，领悟方程的意义

师：刚才这位同学给我们带来了一个新名字，“方程”。老师想问一问，你们知道这个名词吗？它到底有什么特定的意义呢？

学生小组活动，发表自己的见解，引发学习争论。

生：我认为只要有字母就行了，它就是方程。

生：不对！应该是等式。

生：都不对！像A+B=B+A，这个是等式，我爸爸昨天和我讲，它就不是方程。

……

师：有这么多的意见，那到底怎样的式子才是方程呢？

生：就像刚才的②、④一样，它们是等式，而且含有x。

生：老师我的理解是方程必须是等式，含有未知数，就是有不知道的数，不一定就是x。像（   ）+2=5我认为也是方程。

生：他的说法我赞同。我还见过这样的：a+8=10， b-25=56……

师：有这么多的辩论，从中你收获了什么？

生：方程一定是等式，但是等式不一定是方程。如1+2=3，因为它没有未知数。

生：方程中一定有未知数，但不一定都用x来表示。

生：方程是等式，一定含有未知数。

……

师：总结得很好，抓住了方程的意义的要领。你能根据自己的理解写出一组方程吗？

学生自主练习，写出自己的方程，并在小组中交流讨论。

展示学生的学习成果，总结方程的意义。突出方程的两个核心要点。

（设计说明：让学生经历等式、不等式的解读与辨析，促进学生思维的深化，也使方程的概念在交流比较中展现出来，在自主分析中凸显出来。学生一方面能把握等式与不等式的关系，能够辨析等式的存在;另一方面还有利于学生发现这些式子都含有字母x，明白未知数的存在。并把等式、未知数融合在方程的感知当中，当学生提出质疑，师生在互动释疑过程中，进一步把握方程的本质要义，促进对方程意义的理解。同时，让学生写出自己喜欢的方程，不仅有利于学生对方程的理解，更有助于学生领悟未知数的多元性，还能拓展方程的视角，让学生获得最科学、最有意义的方程知识。）

四、引用，深化理解

（一）读一读式子，归归类别

① 4+3y=10      ② 6+2a

③17-8=9         ④ 7-b>3

⑤ 8x=0             ⑥18÷a=2

⑦ 3y+2x=15   ⑧ 4×80=2x-60

上面的8个式子中：不等式有（   ），等式有（    ），方程有（      ）。

（二）明眼辨真伪，判断对错

①等式都是方程。（   ）

②□÷8=8，它是一个方程。（   ）

③2x=0也是方程。（   ）

④方程是含有未知数的式子。（   ）

⑤含有字母的等式叫方程。（   ）

（三）编一编，写写式子

①100元不够买一台电子琴。

（学生推断出只能写出不等式，不能用方程表示。）

②320元正好买4只篮球。

（学生找准等量关系，学习用方程表示。）

（设计说明：通过不同形式的训练，旨在让学生进一步理解方程的基本意义，明晰等式、不等式、方程之间的内在关联性，从而建构正确的方程观。训练阶段安排三组练习，第一组是基本的选择，目的在区分等式、方程等概念，使概念更加清晰;第二组是判断，主要是帮助学生理清概念的本质意义，从而明晰方程的意义;第三组是利用给定的条件引发编写方程的思考，通过能否找出等量关系的思考来帮助学生建构初步的方程思想，让学生感受方程意识的作用，也为后续列方程解决问题提供一种思维范式。）

五、反思，提升学习

（一）本节课学习了什么内容？你有哪些收获？

（二）讨论：等式、不等式、方程你是怎么理解的？

（三）说说方程的基本要素，理一理字母与未知数之间的联系。

教师小结：同学们，方程知识是解决很多实际问题、数学问题的金钥匙，我们一定要理解好它，记牢它的特点。下面让我们了解一下方程知识在我们古代数学史中的主要成就吧！

课件展示：《九章算术》相关知识。（略）

（设计说明：在课的最后让学生互相介绍学习所得，一方面促使学生回顾学习的历程，巩固学习探索的过程;另一方面培养学生的反思能力，促进学生学会自己审视学习历程。在自主回忆交流共享的过程中，促使方程概念在学生的记忆中得到更进一步的强化。课外知识的补充环节，让学生了解到在中国古代数学中方程知识的成就，提高学生学习数学的兴趣，激发学生亲近数学的情感。）

（江苏省宝应县射阳湖镇水泗小学   225809）