平方差公式可以这样验证
2015-09-10丁楠
丁楠
上周老师组织我们进行了“拼图·公式”的数学活动,大家受益颇多. 如何通过拼图验证平方差公式呢?课后,我们活动小组的四位同学进行了深入细致的探究,先后归纳出三种不同方法,现分别介绍如下.
方法一:拼成长方形
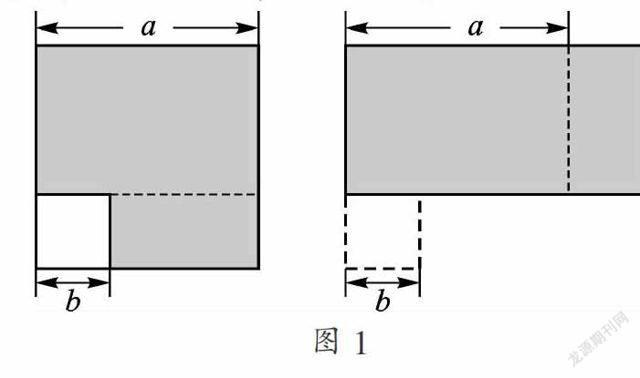
如图1,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),然后将阴影部分剪拼成一个长方形,分别计算这两个阴影部分的面积,可验证平方差公式.
验证:从边长为a的正方形中剪去一个边长为b的小正方形,则左图的面积可以表示为:a2-b2;将阴影部分拼成一个长方形,则右图的面积可以表示为:(a+b)(a-b). 因为这两个阴影部分的面积相等,所以a2-b2=(a+b)(a-b).
方法二:拼成平行四边形
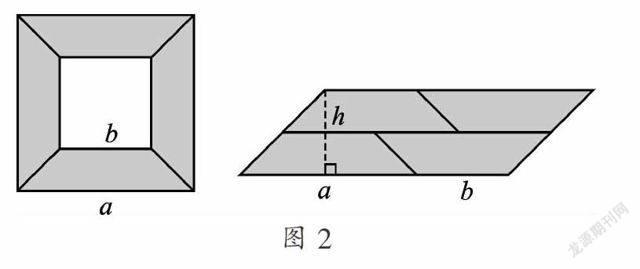
从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形,然后拼成一个平行四边形(如图2). 那么通过计算阴影部分的面积也可以验证平方差公式.
验证:从边长为a的大正方形纸板中挖去一个边长为b的小正方形,则左图阴影部分的面积为a2-b2.
∵每个小等腰梯形的高为,
∴平行四边形的高等于一个等腰梯形高的2倍,即h=a-b,
∵左图阴影部分的面积与右图平行四边形的面积相等,
∴a2-b2=(a+b)(a-b).
方法三:拼成等腰梯形
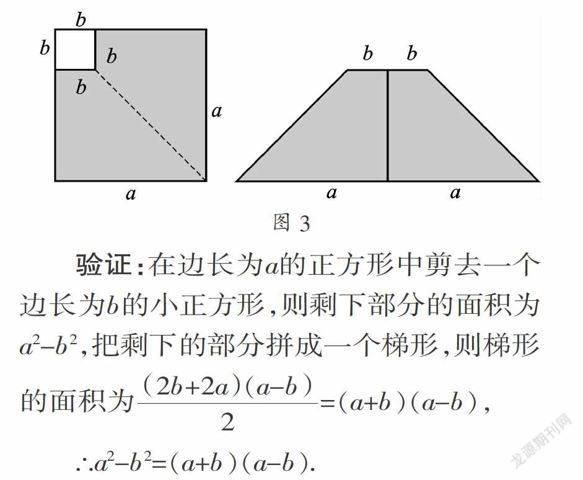
如图3,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了平方差公式.
验证:在边长为a的正方形中剪去一个边长为b的小正方形,则剩下部分的面积为a2-b2,把剩下的部分拼成一个梯形,则梯形的面积为=(a+b)(a-b),
∴a2-b2=(a+b)(a-b).
赵老师点评:在数学活动中,学生分组拼图,在拼出长方形、平行四边形、等腰梯形的情况下都能验证平方差公式,他们通过活动积累了经验,体会了数形结合的数学思想,学会了把面积计算两次(抓住拼图前与拼图后面积相等)列出等式,从而提炼出平方差公式. 让同学们亲身感受到数与形的完美结合,真好!
(指导教师:赵 军)
