爱“拼”才会赢

侯宇飞

今天，老师带领我们一起走进数学实验室，开展了一次拼图验证公式的活动，大家热情高涨. 实验课上，按照老师的指导，我所在的学习小组也对拼图做了一些尝试，现把结果与大家分享如下.

一、 拼图寻卡片

实验工具：如图1，正方形卡片A类、B类和长方形卡片C类各有若干张.

实验目的：如果要拼一个长为（a+2b）、宽为（a+b）的大长方形，那么需要C类卡片______张.

1. 拼图

我们先按照定下的大长方形的长和宽画出草图（如图2），然后在此长方形中先“拼”出正方形卡片A类和B类，剩下的就是长方形卡片C类的“地盘”了，图2简直就是一个会说话的图形，答案跃然纸上！C类共需3张.

2. 验证

由拼成的长方形长为（a+2b）、宽为（a+b）可知，其面积为：（a+2b）（a+b）=a2+3ab+2b2，由等式右边可见：1个a2、3个ab、2个b2，即需要A类卡片1张、B类卡片2张、C类卡片3张.

二、 拼图验证公式

（一）

实验工具：如图1，正方形卡片A类、B类和长方形卡片C类各有若干张.

实验目的：试用拼图的方法验证完全平方公式：（a+b）2=a2+2ab+b2.

1. 拼图

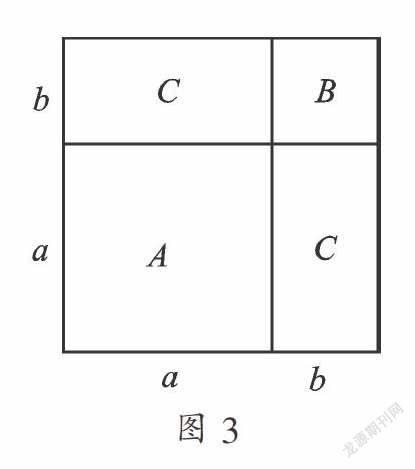
确定拼图方案，设计边长为（a+b）的正方形. 分别取A类、B类卡片各1张、C类卡片2张，按照如图3所示的方式进行拼图.

2. 验证

我们小组的同学在计算该正方形面积时，出现了两种方法，一种是直接算，S=（a+b）2 ，另一种是分开计算4个图形的面积之和，即S=a2+ab+ab+b2，因为计算的是同一个正方形的面积，所以（a+b）2=a2+2ab+b2. （二）

实验工具：边长为a的大正方形卡片1张，直尺、铅笔、剪刀等工具.

实验目的：用拼图的方法验证平方差公式：a2-b2=（a+b）（a-b）.

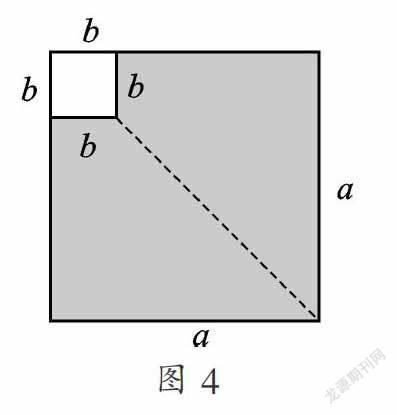
在边长为a的正方形纸片中，剪去一个边长为b的小正方形（a>b）（如图4），把余下的部分沿虚线剪开后，拼成一个新的图形，验证平方差公式（用含a、b的代数式表示）.

1. 拼图

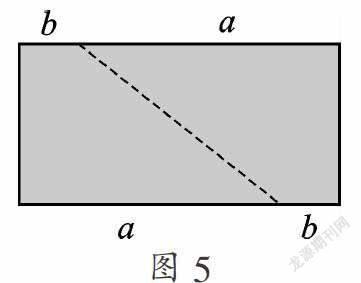
把两个直角梯形拼成一个长为（a+b）、宽为（a-b）的长方形（如图5）.

2. 验证

拼图前（如图5）阴影部分的面积为：a2-b2，拼图后阴影部分的面积为：（a+b）（a-b），故能验证平方差公式：a2-b2=（a+b）（a-b）.

3. 惊喜

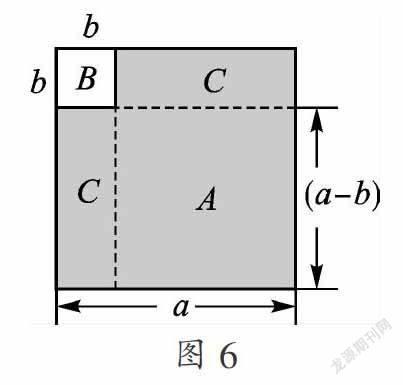
如图6，图中正方形A的边长为a-b，面积为（a-b）2，能不能借助面积关系验证完全平方公式（a-b）2=a2-2ab+b2呢？我们小组进行了如下尝试：

（指导教师：赵 军）