是“测”，更是“策”

陈晶

“估测作为算术估计的主要组成部分之一，被视为个体数学能力早期获得的重要渠道，构成了数学认知的一个重要领域。目前它已成为国际基础数学教育改革中十分重视的内容。许多国家的数学课程标准中都不同程度规定了估测的教学要求。”我国正式将估测纳入小学数学教学内容是在《数学课程标准（实验稿）》之中，《数学课程标准（2011年版）》对估测的内容进行了适当调整。但在实际教学过程中，常常出现对估测的误解和片面解读：有些教师常常误以为估测就是随意猜测，还有的教师只是把估测的教学仅仅执行为猜测和测量验证等，对估测的误读和片面理解使得估测教学的效益大打折扣。如何理解估测教学的意义，培养学生的估测能力呢？笔者以“长方形和正方形的面积”为例谈谈估测的教学实践与思考。

一、理解意义，把握价值

估测就是一种测量估计，“是一种非常实用的日常数学技能，被看作是没有工具的物理测量。”心理学上，把是否使用工具作为是否进行估测的标准。常用的有效估测策略有：“单位迭代、参照点（又称基准点）、在估计前把估计物进行心理转换。”

《数学课程标准（实验稿）》在1～3年级学段目标里提出：“获得初步的测量（包括估测）、识图、作图等技能。”在内容标准中指出：“能估计一些物体的长度，并进行测量。”“结合实例认识面积的含义，能用自选单位估计和测量图形的面积，”“探索并掌握长方形、正方形的面积公式，能估计给定的长方形、正方形的面积。”在4～6年级学段目标里提出：“发展测量（包括估测）、识图、作图等技能。”在内容标准里指出：“能用方格纸估计不规则图形的面积。”在《数学课程标准（2011年版）》的学段目标里未直接提及相关的估测要求，在1～3年级内容标准里面指出：“能估测一些物体的长度，并进行测量。”“探索并掌握长方形、正方形的面积公式，会估计给定简单图形的面积。”在4～6年级内容标准里面提出了与《数学课程标准（实验稿）》相同的要求。从上述变化可以看出，《数学课程标准（2011年版）》适当降低了估测的要求，不再把估测作为一项技能。从对面积估测的教学内容来看，这里的估测不仅有不借助于工具的物理测量，也包括借助简单的工具（方格纸）测量不规则图形的面积。所以，估测教学不仅包括让学生学会不借助工具进行测量，也包括学会借助工具获得相关图形面积的近似值。

二、丰富表象，积累经验

估测也是一种测量，这里的测量工具是单位表象、生活中的参照物，在教学过程中，既要丰富学生对于单位表象的认识，熟悉生活中常见的物体表面的面积，也要加深学生对于面积测量意义的理解，积累面积测量的经验。

（一）多维度认识面积单位

常用的估测策略之一是“单位迭代”， 也即“估计者在估计时，使用某个标准单位（如厘米），反复将标准单位与估计物相对照，记住上次标准单位结束的位置，开始下一次对照，计算单位的数目，从而得出估计结果”。能够使用“单位迭代”策略的基本前提之一就是形成比较稳定的单位表象，教学过程中，需要通过不同层次的活动让学生丰富对面积单位的体验。如在认识平方厘米的过程中，可以安排一系列的活动：做一做，自己尝试做1平方厘米的小正方形；看一看，让学生看看1平方厘米正方形的大小；想一想，闭着眼睛想一想1平方厘米的大小；找一找，从生活中找到面积接近1平方厘米的物体的面等。学生对于面积单位的体验越丰富，形成的表象就越稳定，在估测的过程中，主动运用“单位迭代”策略估测物体表面面积的能力就越强。

（二）丰富物体表面面积的认识

选择合适的参照物来估测物体表面的面积也是常用的估测方法之一，所以，除了让学生形成基本面积单位比较稳定的表象外，还要形成对于生活中常见物体表面面积的理解与记忆。在教学过程中，一方面利用面积单位对实际的物体进行测量，在测量中形成对生活中相应物体表面面积的认识，另一方面在完成“在（ ）里填合适的单位”时（如图1），不仅让学生填合适的单位，还要找到具体的面或者与之面积相近的面，让学生理解其实际面积。还可以让学生根据具体描述的面积，找一找生活中与之相近的物体的表面。通过这样的活动，丰富学生对于生活中常见物体表面面积的认识，为后续学习找到合适的参照物进行估测打下基础。

图1

（三）拓展度量方法

学生在刚开始认识面积单位时，对于实际物体表面的面积都是运用面积单位进行量化，在后续的学习中，还要让学生运用实际生活中的已知物体的面去度量未知物体的面。在教学过程中可以设计类似的问题情境：明明妈妈的手机面的面积大约是40平方厘米，你能够想办法量出练习本封面的面积吗？通过解决这种问题拓展面积度量方法。

对于较为规则的图形面积的度量，除了让学生理解可以运用面积单位进行直接测量外，还要基于图形边的长度与面积单位之间的关系，让学生学会间接测量，理解间接测量的方便性。在学习长方形和正方形面积的过程中，让学生不仅知道长方形的面积等于长乘宽，更要理解长在面积度量过程中表示的是什么？宽在面积度量过程中表示的是什么？把握直接测量与间接测量之间的联系。

三、灵活运用，提升策略

基于《数学课程标准（2011年版）》对估测的理解，估测既是一种不用工具的测量，也包括运用测量工具获得一个近似值。教学过程中，一方面要结合具体的问题让学生丰富估测方法，另一方面也要让学生学会描述估测的结果，不断提高估测能力。

（一）工具测量，合理描述测量结果

估测首先是一种测量，在让学生估测的最初阶段，要基于面积单位以及图形面积的本源意义，让学生利用合适的工具对一些物体表面的面积进行测量，学会描述测量结果的近似值。

1.自选工具测量，初步把握结果

在学生认识了面积单位后，可以让学生运用面积单位去测量物体表面的面积（如图2）。在让学生运用1平方米测量的过程中，如果比1平方米多一些可以忽略不计，如果比较接近1平方米则需要看成1平方米。通过这样的简单操作，让学生初步获得对于度量结果处理的经验。

在教学过程中，还可以让学生运用已知物体表面的面积去测量生活中常见物体表面的面积。如知道了文具盒盖的面积，可以运用文具盒盖的面去度量桌面，看看桌面大约有几个文具盒盖的面积，然后算出结果。通过这样的估测过程，丰富学生对于估测意义的理解，也培养了学生对于结果的处理能力。

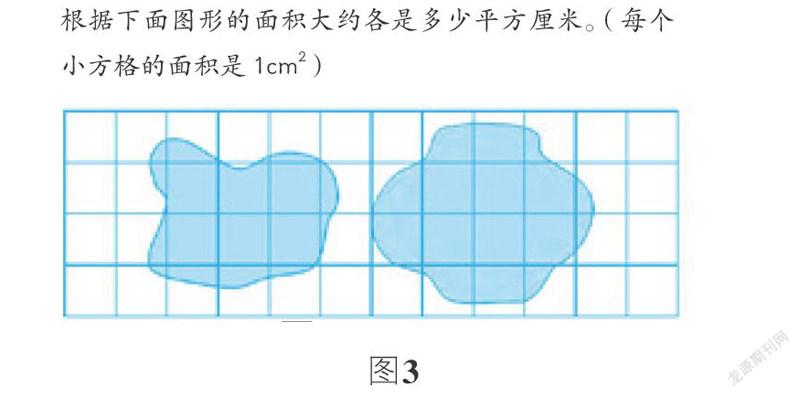
2.方格测量，形成不同的描述方法

学生初步获得了描述测量结果的近似值的经验后，还要让学生运用面积单位去测量不规则图形的面积，获得运用不同方法描述结果的经验。在教学图3问题的过程中，对于结果的处理，可以根据前面的估测经验，把所有接近整格的都看成整格的，确定最后的结果；也可以进一步观察图形所占的格子，有些不足整格的比半格大一些，有些不足整格的比半格小一些，可以把所有的不足整格都看成半格来估计它的面积；还可以找到所有的整格，确定图形面积的下限，再找到所有不足整格的数量，算出整格数量和不足整格数量的总和，确定图形面积的上限，运用上下限确定图形面积的范围。通过不规则图形面积的估测，进一步丰富学生对于结果的处理方法，让学生在实际的估测过程中能够根据不同的要求选择不同的估测方法。

（二）直觉猜测与测量验证相结合，培养学生的量感

学生对于不用工具的估测，首先是一种直觉猜测，在学生进行直觉猜测后，还需要进一步通过面积单位进行测量，让学生调整原有头脑里的认识，通过这样不断反复的过程，培养学生的量感。如让学生猜一猜课桌面的面积，学生在猜测的过程中，基于对面积单位及数的感觉的认识，形成了对桌面面积单位数量的初步认识，最后通过测量结果与猜测结果的比较，让学生调整头脑里原有的猜测结果，在头脑里形成对于桌面面积新的认识。

（三）有效“单位迭代”，培养学生的空间观念

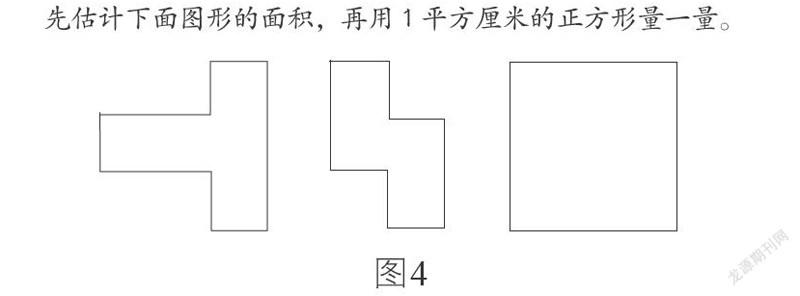
“单位迭代”是学生常用的估测策略，学生在估测学习的初始阶段，要通过富有启发性的情境，让学生主动尝试进行“单位迭代”估测。如教学图4所示习题的过程中，受图形形状的启发，学生会想到在脑子里摆一摆面积单位进行“单位迭代”估测，最后估测出每个图形的面积，学生在“单位迭代”的估测过程中，一方面主动提取了原有的面积单位，另一方面把原有的面积单位在头脑中根据度量的经验进行主动拼摆。通过这样的“单位迭代”估测过程，有效培养了学生的空间观念。

（四）利用参照物估测，培养学生的推理能力

在一个图形中面积单位的数量较多时，此时“单位迭代”策略就不太容易估测出图形的面积，需要调整估测的思路，找一个合适的参照物来估测。在教学过程中，可以让学生描述一个较小物体表面的面积，然后估测一个与其相关的面积，在这样的情境中让学生主动运用选择参照物的方法，提升估测水平。如知道了教室门面的面积后，再让学生去想一想墙面的面积大约是多少，有了对门面面积的了解，学生在估测的过程中自然选择门面这个参照物去估测墙面的面积，可以将墙面按门面的大小进行划分，也可以在大脑里想象出在墙面上移动门面，通过这种找参照物估测的方法，培养学生的推理能力。

（五）利用公式估测，加深对公式意义的理解

学生学习了长方形、正方形的面积计算方法后，对于一些长方形和正方形面积的计算可以让学生依据公式，估测出长方形的长和宽，然后算出图形的面积，降低学生估测的难度。在教学图5所示习题的过程中，学生交流并回忆其中的估测方法，通过不同方法之间的比较，理解估测出长方形的长和宽，最终用公式算出面积是较为简单的策略。

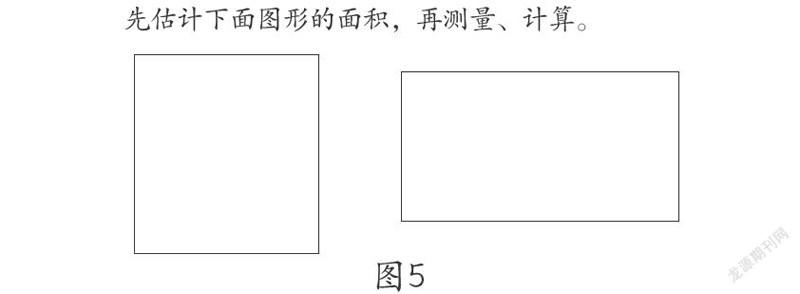
对于实际生活中一些常见物品如桌面、篮球场等面积的估测，可以进一步借助简单的身体上的尺估测出长和宽，最后再算出其中的面积，丰富估测的方法。

（六）复杂图形转化成简单图形，加强图形之间的联系

生活中的图形不一定都是标准的长方形或正方形，这些图形面积的估测相对而言较为复杂，对于这样的图形，可以引导学生仔细分析图形的形状，可以将其中的一些图形看成已经学过的长方形或正方形进行估测，也可以将一些图形进行合理的分解与组合，最终拼成长方形或正方形。例如，椅子表面是梯形的，学生还未曾学过梯形的面积，可以将椅子的面看成一个近似的长方形，然后估测其面积；一些更复杂的图形（如图6），可以引导学生进行简单的切割与拼组，最终转化成一个长方形来估测其面积。通过这种图形的转化，加强图形面之间的转化能力，提升估测的水平。

估测，是一种测量，这种测量由于受工具的限制，我们只能获得一个近似值，需要我们选择合适的方法去描述结果；估测更是一种解决问题的策略，这种策略体现在对于不同的图形，我们要能够根据图形的特征灵活选择合适的策略进行估测，在后续学习的过程中，还需要根据已有的经验进一步提升估测的水平。这样的估测教学，才能够促进学生的经验不断积累，思维水平不断提升，达到估测教学的真正目的。

（江苏省南通崇川学校 226014）