巧引导，促修正

邓林树

学生的学习是和错误相伴的过程，错误恰恰反映出学生的学习困难所在。出错不可怕，可怕的是不让出错，或是出错了不予关注。教师不仅要允许学生出错，包容、接纳他们的错误，更要通过有效引导，促进学生修正错误。

一、当学生出现认知偏差时巧妙引导

比如，教学“数一数与乘法”起始课，在课末小结时，我问：“同学们，通过这节课的学习，你学到了哪些本领？”谁知一位学生冒冒失失地回答：“我学会了加法。”我不由得一愣，真有点哭笑不得。但我又换位思考了一下：这节课讲乘法我就是从几个相同的数连加引入的，站在学生的角度，他这样回答也是在情理之中，“错误”当中其实含有“合理”的成分。于是我将错就错，因势利导：“那你学会了怎样的加法呢？”“我学会了加数相同的加法。”“这样的加法还可以用什么方法表示呢？”“还可以用乘法表示。”“那么，这节课你学会了哪些新的本领呢？”至此，这位学生给出满意的回答就水到渠成了。这样，既保护了学生的自尊，帮助他理清了思路，又在不知不觉中强化了本节课的重点和关键，突出了乘法的本质，使全体学生对乘法的认识得到了进一步深化，意外的错误带来了意外的收获。

二、当学生列式不够规范时巧妙引导

有一次，我让学生做了这样一道题：枫叶服装厂接到生产2400件衬衫的任务，前3天完成了40%。照这样计算，完成这项生产任务一共要用多少天？课堂巡视时，我发现一位同学只写了一个得数“7.5”。我问他：“怎样列式呢？”他摸着后脑勺很不好意思地说：“我知道结果是7.5，但我不知道该怎样列式。”我说：“你的答案是正确的。没关系，你怎样想就怎样列式吧！大胆地列出来，让我见识见识。”不一会，他列出了这样的算式：

40%=3天

40%=3天

1-40%-40%=20%（天）

20%=3÷2=1.5（天）

3+3+1.5=7.5（天）

看到这样的算式，我笑着对他说：“你的思路其实很清晰，列式也很有意思，请你到黑板上写出来吧！”他高兴地上台写下了算式。

面对这样的算式，全场哗然。有的说：“太好笑了，什么意思哟，40%怎么会等于3天呢？”有的说：“好像也有点道理吧，最后结果也是7.5。”

这时我示意同学们保持安静，先听他解释。他振振有词地说：“题目里说3天完成了40%，说明完成40%就需要3天，所以40%=3天，再完成一个40%又需要3天。总的就还剩下1-40%-40%=20%，20%正好是40%的一半，所以20%=3÷2=1.5（天），一共就是3+3+1.5=7.5（天）。”

听了他的解释，许多同学不住地点头，但仍有部分同学持反对意见。这时我又说：“这位同学的解法很有创意，只是有的地方还不够规范，下面我们一起帮助他纠正一下，好吗？”

通过讨论，同学们很快就意识到：完成40%需要3天，但不能用40%=3天表示，这个过程应省去；同理完成剩下的20%，也不能用20%=3÷2=1.5（天）表示，应写成3÷2=1.5（天）。按这种思路可以只列四个算式，即1-40%-40%=20%，40%÷20%=2，3÷2=1.5（天），3+3+1.5=7.5（天）。

数学是非常严谨的，该怎样列式是有讲究的。同学们要是出现了一些不规范的列式，教师不应该回避，而应该采取积极有效的措施加以引导，从而使他们及时修正错误。

三、当学生审题出现失误时巧妙引导

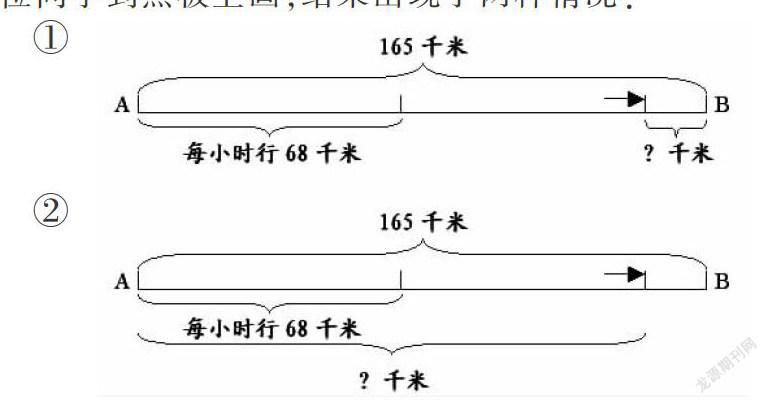
画画草图，对我们正确解答数学问题有很大的帮助。画草图，可以画示意图，也可以画线段图，不要求画得很标准，只要能说明问题就可以。但是许多学生怕麻烦，懒得画草图，导致本不该出现的错误又出现了。我曾出过这样一道毕业会考模拟题：A、B两地相距165千米，一辆小客车从A地出发，每小时行68千米，2小时后离A地有多少千米？考前我想这是很基本的行程问题，按理说没多少同学不会做。考后我惊讶地发现正确率不到40%，有60%左右的同学都错误地列式为：165-68×2=29（千米），成了失分最严重的一道题。为什么会这样呢？这显然是没有搞清楚“小客车2小时后离A地有多少千米”指的是哪一段路程造成的。讲评时，我引导学生先画线段图，同时也请两位同学到黑板上画，结果出现了两种情况：

①

②

然后我引导学生结合线段图分析，学生很快找到了错误所在。图①是不符合题意的，求的是“小客车2小时后离B地有多少千米”，也就是剩下的路程，可以用“165-68×2=29（千米）”来求。图②才是符合题意的，求的是小客车2小时行的路程，也就是“小客车2小时后离A地有多少千米”，应该列式为68×2=136（千米）。

四、当学生的解答脱离实际时巧妙引导

比如学生做人教版六年级上册P54第2题（如右图），学生大多列式为42÷15×6﹦16.8（米）。他们认为先用“42÷15”求出每层有多高，因为小萍家住6楼，再“×6”就对了。这些同学疏忽了“6楼的楼板到地面的高度”实际上只有5层楼的高度。面对这样的错误，我先引导学生联系实际思考：我们学校二年级在几楼上课？（二楼）二楼的楼板到地面有多高？是两层楼的高度吗？（不是，是一层）我们在几楼上课？（四楼）那我们这一层的楼板到地面的高度相当于几层楼的高度？多媒体教室在几楼？（六楼）多媒体教室的楼板到地面的高度相当于几层楼的高度？因为设身处地，这些问题很快得到了解决，“6楼的楼板到地面的高度实际上只有5层楼的高度”这个关键性的问题得到了学生的认可，错误得以纠正。

错误是学生在学习过程中思想、经验最真实的暴露。从某种意义上说，错误是一种宝贵的教学资源。学生经历错误后，如果能在教师的引导下，认识到出错的原因，修正错误，那么学生就会对自身的错误理解得更深刻、记忆得更牢固。