建筑中的数学之美

陈泳全

希腊哲学家毕达哥拉斯认为“万物皆数”，并将自然纳入人类的理性思考范畴。在建筑发展中，数学是建筑结构、力学的基础，以投影几何为基础的画法几何和阴影透视的运用，是近代建筑学产生的催化剂;概率和统计则是建筑学进行社会调查研究的重要工具……建筑中无时无刻不蕴含着数学的抽象、理性和精确。而数学的精确性与大胆的幻想结合起来就是美。数学在建筑中的应用不仅蕴含着理性，还呈现出人类对数学之美的感性体验。

 希腊埃皮达鲁斯剧场平面图

几何之美

人类对几何图形的认识主要源于对自然几何形态的感知与模仿，例如太阳、月亮、植物茎干、果实、山川等等，由此产生了圆、圆柱、三角等几何图形。对重力的体验，对水平和垂直的观察体悟，使人类创造出自然界几乎找不到的几何形态——矩形、立方体。无论是模仿还是创造，几何形态成为人类进行建筑实践的基础，也是人类对美的感知与表现。

几何学（Geometry）这个词来自古埃及的“测地术”。那时，尼罗河每年会有一次洪水泛滥，促成了古埃及文明的产生。洪水到来时，会淹没两岸农田;洪水退后，又会留下一层厚厚的河泥，形成肥沃的土壤。每当洪水退去后，原有的土地界限不复存在，需要重新丈量界定。法老政府按土地征税，也要丈量计算土地面积，这就促使了古埃及几何学的发展。4500年前，古埃及人建造的建筑史上的奇迹——胡夫金字塔，既是工程学的巨大成就，也表现出古埃及几何学的辉煌。该金字塔的塔高约146.6米（顶端剥落前），塔身倾角为51度52分，塔底部为边长230米的正方形（原长），胡夫金字塔的4个斜面正对东、南、西、北四方，误差不超过圆弧的3分，在当时的条件下，能达到如此建造精度令人难以置信。

在希腊建筑中，我们也到处都能看到基本几何形的运用。在构造建筑物时，希腊人喜欢把绳索系在钉子上，将其拉直旋转，从而画出他们设计的直线和圆弧。公元前4世纪，希腊埃皮达鲁斯（Epidaurus）的一座剧场展现了希腊建筑与几何学之间的联系。埃皮达鲁斯剧场以山坡上凿除的石块为座位，这些座位共同构成一种不断增大并升高的半圆形图案，其中最大的一个半圆的半径约为61米。埃皮达鲁斯剧场具有优秀的声学效果，站在露天舞台中间的表演者的声音，即使在最后一排的观众也能听到。至今，该剧场仍为古希腊夏季戏剧表演项目的热门之地。

罗马人继承了希腊人在几何方面的成就，并进一步发扬创新。希腊人在半山坡上凿出大剧院，用山体支撑倾斜排列的半圆形座位，而罗马人则是在城市的平地上修建，如椭圆形的罗马斗兽场。罗马人通过对混凝土、石头砌筑技术的掌握，结合希腊人的几何成就，扩展出拱券结构、穹顶结构等技术，进一步实现对几何形态的塑造。如罗马万神庙的穹顶直径为43米，穹顶最高点距地面约为43米，内部空间接近一个纯粹的球体，它将罗马工程师的力量与希腊的审美形式天衣无缝地结合在一起。

现代建筑的发展与古典建筑相比，更主张注重功能性，摒弃繁复的装饰，追随简洁纯粹之美，因此，简洁纯粹的几何形体成为现代建筑师创作的基本手段。例如现代建筑大师勒·柯布西耶的成名之作萨伏伊别墅，这是一个完美的功能主义作品，简单到几乎没有任何多余装饰的程度，纯粹的几何形体开拓了又一个新的审美时代。美国建筑师富勒1967年为蒙特利尔博览会美国馆的设计，又一次展现了纯粹几何形体的魅力，这个球形的建筑不仅是形的纯粹，更是其三角形金属网状结构的精妙应用，体现了以最小的材料创造出最大的内部空间的建筑理念。建筑大师贝聿铭在卢浮宫改扩建的设计中借用古埃及的金字塔造型，并采用了玻璃与金属材料，简洁纯粹的几何形体不仅折射出现代艺术的光辉，同时与古老的宫殿形成了功能与形式上的完美结合。

 万神庙剖面演示

数列之美

希腊建筑的美在很大程度上取决于尺度和比例，勒·柯布西耶曾这样评说：“帕提农给我们带来确实的真理和高度数学规律的感受。”古希腊人通过详细观察自然界中的种种事物，发现凡是美的物体在形式上都具有和谐的比例关系。比例，简单地说就是部分与部分、部分与整体之间的数学（倍数）关系，这种认识影响了整个西方建筑的发展。这种数学关系在数学中，被称为数列，即是把数字按一定的规则加以排列，如著名的斐波那契数列（1、1、2、3、5、8、13、21、34、55、89…）：任意一项是其前两项之和，且相邻两项之比逐渐接近黄金分割。

黄金分割（Golden Section）是数学上一种经典的比例关系。长方形的长为a，宽为b，如果 b：a =（a-b）： b，则为黄金比的长方形。根据算式可以求得：b≈0.618a，a≈1.618b。

公元前3世纪，古希腊数学家欧几里德撰写的《几何原本》，系统论述了黄金分割，成为最早的有关黄金分割的论著。中世纪后，黄金分割被披上“神秘的外衣”，德国天文学家开普勒称之为“神圣分割”，到了19世纪，黄金分割这一名称逐渐通行。黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值。

对称是自然界很重要的一种现象，同样也是一个重要的数学概念。它是一种特殊的比例关系，在空间和形式上能够表现出一种庄重、稳定、平衡的美。在各国建筑发展的历程中，我们都能看到建筑师们对于比例关系的不懈追求，也因此，这些建筑常常呈现出平衡、和谐、秩序的美感。

 罗马斗兽场

在希腊数学逻辑化、几何化、理念化的特征影响下，希腊建筑强调形和比例，注重立面和单体造型。而古代中国的数学更倾向于以问题为中心的算法体系，在建筑上体现的是对数的强调，注重构件、剖面和群体组合。中国古建筑的所有构件之间都有一种模数关系，“材”就是宋代建筑上的模数。可以说，模数是中国传统建筑数学之美的内在体现。

黄金分割的另类故事

人在周围环境温度为22～24℃时感觉最为舒适。因为人的体温37℃与0.618的乘积为22.8℃，这一温度中，人体的新陈代谢、生理节奏和生理功能均处于最佳状态。

 使用黄金分割比率的帕提农神庙

复杂之美

机器时代的传统科学倾向于强调稳定、有序、均匀和平衡，最关心封闭系统和线性关系;而新的科学更关心现实世界无序、不稳定、多样性、不平衡、非线性以及瞬时性的复杂关系。科学对复杂性的探索，导致了数学越出了传统的概念和对象：从单个或少数变量到多变量，从低维空间到高维空间;从线性问题到非线性问题;从连续、稳定到间断、突变和不稳定;从平衡的、守恒的、可逆的到非平衡的、耗散的、不可逆的;从决定性的、有序的、周期性的、对称的到随机的、无序的、非周期性的、对称破缺的;从确定到模糊。数学的发展不仅提供了新的发现和新的论断，更重要的是表达了新的思维方法、新的认识论和新的世界观，在建筑领域中影响了一批建筑师，产生了新的、更多元的审美趋向。

美国建筑大师弗兰克·盖里经常采取拼贴、混杂、并置、错位、模糊边界、去中心化、非等级化、无向度性等各种手段，挑战人们既定的建筑价值观，他的设计风格颠覆了几乎全部经典建筑美学原则。其设计的西班牙毕尔巴鄂古根海姆博物馆，整个建筑由一群外覆钛合金板的不规则双曲面体量组合而成，其形式超出了传统几何形态及手段所能描述的范畴，必须在计算机辅助设计软件、计算机辅助制造系统、3D打印等手段的帮助下才能得以实现。其建成后，出乎意料地受到人们的追捧，也证明着数学的复杂性形成了一种新的审美观。

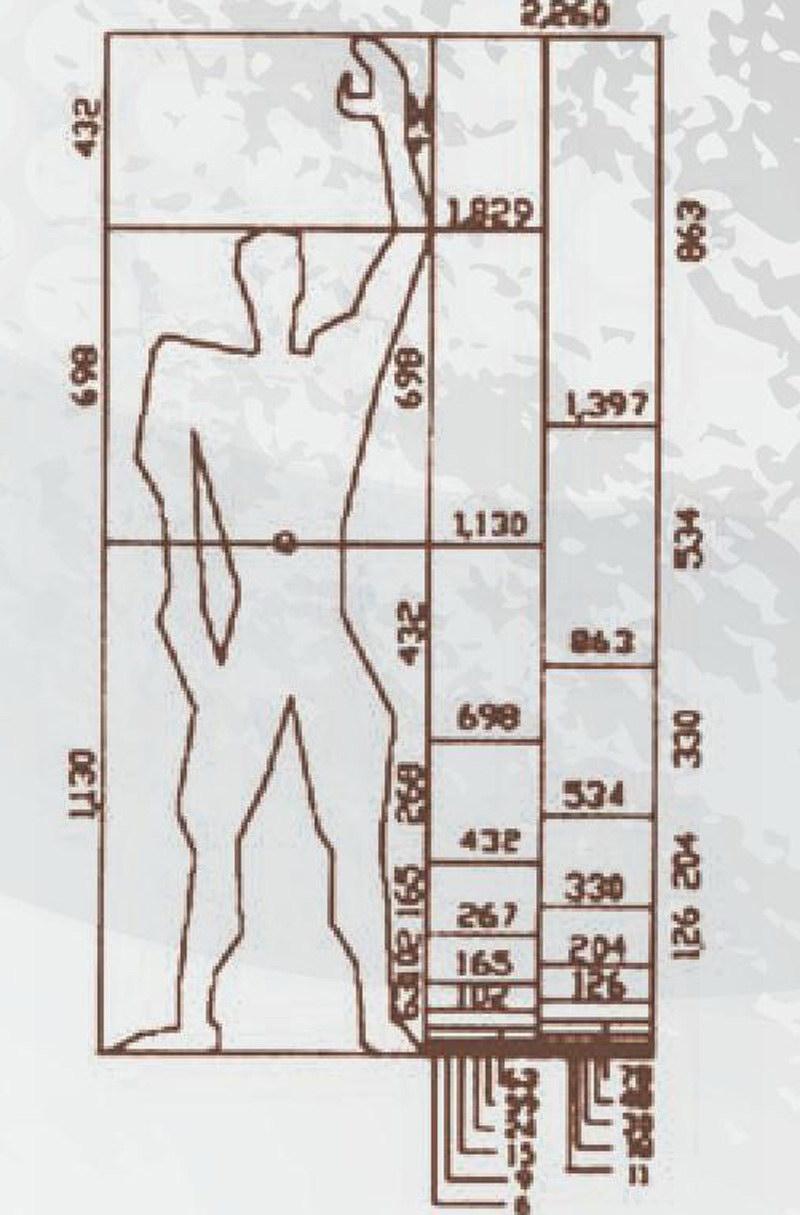
 勒·柯布西耶著名的人体模数图，也运用了斐波那契数列与黄金分割

著名女建筑师扎哈·哈迪德曾在黎巴嫩就读过数学系，良好的数学素养，使她能够大胆利用空间，追求自由、精确、流畅的几何形态。她将一种自由、非线性、动态的形体控制转化为一种独特的审美风格。如她设计的盖达尔·阿利耶夫文化中心，在形式上精心设计的起伏、分叉、折叠还有自由的形态，使广场的表面变成一个多功能的景观建筑。建筑四周的广场与建筑的室内空间之间，建立了一种连续而流动的关系。建筑形态模糊了建筑的边界，将复杂的非线性数学关系消隐在建筑之中，却留下了非凡的美感体验。

拓扑学是新数学的一个方向，它研究几何图形和空间在一对一的双向连续变换下不变的性质，即拓扑性质。一个几何图形任意“拉扯”，只要不发生割裂和粘接，可做任意变形，称为“拓扑变形”。两个图形通过“拓扑变形”可以变得相同，则称这两个图形是“拓扑同构”。由此可见，球和立方体同构，与轮胎不同构。欧美小住宅和中国四合院的拓扑结构不同，前者与球同构，后者与轮胎同构。

 哈萨克斯坦新国家图书馆方案

拓扑突破了传统几何形态中对尺寸、角度和比例的确定性。德国数学家莫比乌斯将一个长方形纸条的一端固定，另一端扭转半周后，把两端黏合在一起 ，得到的曲面就是无限连续的莫比乌斯圈（Möbius Strip）。

在哈萨克斯坦新国家图书馆的方案竞赛中，丹麦BIG事务所的设计作品取得了第一名。他们的设计是将穿越空间与时间的四个世界性经典造型—圆形、环形、拱形和圆顶形—以莫比乌斯圈的形式融合在了一起。BIG事务所设计的2010年世博会丹麦馆，同样采用的是莫比乌斯圈的理念，这座建筑连续的表面即是人们参观的连续界面，功能与空间完美结合。

恩格斯说过：“数学是研究现实世界的空间形式和数量关系的科学”，而建筑恰恰是反映空间形式、数量关系的载体，数学的发展对建筑的发展毫无疑问影响巨大。艺术和数学的本质都是领会事物间的关系，而创造则是从新观点出发作出的一种领会，美，亦是一种领会，让我们在建筑中创造、发现、体验数学之美。

博物馆的出炉

 2010年世博会丹麦馆

建筑师盖里在毕尔巴鄂古根海姆博物馆的设计中采用的设计策略，与汽车设计非常相似。他先在纸面上通过曲线素描和手工塑形曲面模型自由表达他的初始想法，然后用三维扫描仪捕捉实体模型上重要的顶点、边或表面的数据，通过诸如NURBS这样的软件，将其进一步转化成数字三维模型，能够更好地表达流线形状的微妙之处以及彼此之间的细微差别，并达到极高的精度。而后再由计算机控制的三维打印机和多轴铣床制造新的物理模型，将它们与原来的设计相比较，对其形状进行修正和调整，直到设计团队对它们之间的匹配程度感到满意。

 阿塞拜疆共和国盖达尔·阿利耶夫文化中心