金属薄板中导波的模态识别和波速测定
2015-09-04张维刚李凯丽肉孜麦麦提黄志刚项疆腾
张维刚,李凯丽,肉孜麦麦提,黄志刚,项疆腾
金属薄板中导波的模态识别和波速测定
张维刚1,李凯丽1,肉孜麦麦提2,黄志刚1,项疆腾1
(1. 中国计量学院质量与安全工程学院,浙江杭州310018;2. 新疆克州质量与计量检测所,新疆阿图什845350)
按照Lamb波理论,板内导波由多阶对称波和反对称波组成。当波长远大于板厚时,利用经典平板理论对Lamb方程进行简化,此时板内主要有零阶对称波S0和反对称波A0两种模态。认识薄板内声波模态,不仅有助于分析声源性质,提取有效信号,而且可以提高声发射检测中时差定位的准确性。利用PAC公司的Fieldcal标准信号发生器和Nielsen Hsu断铅法作为信号源在0.7 mm薄钢板上进行声波传播实验。通过比较实测波速和理论波速甄别板内的声波模态。实验发现对称波S0实测波速和理论波速比较吻合,而反对称波A0的波速由于频散而较难精确测量。综合两种模态波的波速情况,声发射检测中利用对称波速度进行声源定位计算更加接近薄壁结构声波的传播状况。
模态声发射;Lamb波;波速;平板波
0 引言
模态声发射是利用板波(兰姆波)理论研究板中声发射波的特点,将声发射波形与特定的物理过程相联系,当板中传播的声波波长远大于板厚时对声发射源机制进行有效识别的一种新的声发射检测技术。它能有效区分声发射信号和噪声信号,因而在工程应用中具有巨大的研究价值。
Michael R. Gorman依据经典平板理论对传统声发射(Acoustic Emission, AE)技术进行修正。研究了Lamb波的最低阶对称波(S0)和最低阶反对称波(A0),并在铝板、环氧石墨板上进行断铅实验[1]。Dunegan通过高、低通滤波器研究了离面声源和平面内声源信号的频率占比[2]。耿荣生讨论了不同模式声波的群速度、相速度与频率-厚度关系曲线[3]。刘晶在碳-环氧复合材料上进行实验,证明模态声发射在板材结构的裂纹检测上是有效的[4]。蔡文生发现不锈钢板点蚀信号波的主要模态是S0和A0,而且A0占据信号的主要能量[5]。翟庆宏研究了厚板与薄板上的波速和衰减,波速约5372 m/s[6]。樊保圣在铝板上进行声波传播研究,通过傅里叶变换对模态进行辨识[7]。
总之,许多研究集中在模态声发射技术的可行性上,但对波形模态缺乏直接的认识手段。本研究利用PAC公司的Fieldcal标准信号发生器和国际上通用的Nielsen Hsu断铅法作为激励源,在0.7 mm薄钢板上进行声波传播的模态分析和波速测定,通过比较理论波速和实测波速,提出一种较为简便的模态辨识方法,揭示出波形、波速、门槛值、源频率之间的相互关系。
1 理论分析
1.1 理论速度
从频厚积对相速度关系曲线可见[8],当频厚积小于2MHz·mm时,板内传播的只有S0(扩展波)和A0(弯曲波),卡夫提出一种近似的相速度计算公式[9]:
1.2 模态波引起的薄板振动
薄板上传播的两种模态波,使板发生不同模式的振动,如图1所示。扩展波引起对称模式振动。弯曲波引起反对称模式振动。板内质点位移可以分解为平行于板的分量和垂直于板的分量。AE传感器垂直于板面,所以仪器总是记录模态波的垂直位移分量。
(a) 扩展波
(b) 弯曲波
图1 两种模态波引起的板振动
Fig.1 Tow types of plate vibrations excited by wave modes
1.3 波速计算
传统的AE检测采用时差定位[10]。图2是一个突发信号示意。坐标原点记录信号到达时间,向前延伸256 μs,作为预触发时间,是信号源激发时间,是预触发阶段的波传播时间,可以通过波形图横坐标读取。如果,则必须对采样长度、预触发时间、门槛值进行适当调整。、和门槛值设置密切相关,不同幅值的信号可能因为门槛值高低而被记录或忽略。笔者曾经专门研究过门槛值对定位精度的影响,发现门槛值高低对传感器阵列中部的声源影响较小,而对传感器附近的声源误差较大,这正是受不同模态波激发造成的[11]。波速的实测计算公式为
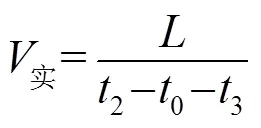
式中,L为声源和收到信号的传感器之间的距离。
2 实验研究
2.1 实验装置
实验仪器为PAC公司的Micro-Ⅱ型声发射检测系统。传感器为R15I-AST型系列(谐振频率为150 KHz)和R6a型系列(谐振频率为50 kHz)。实验对象为0.7 mm×1000 mm×800 mm薄钢板。Fieldcal信号发生器产生的30 kHz和60 kHz正弦波作为R6a型传感器的信号源;铅笔折断信号作为R15I-AST型传感器的信号源。该信号同金属裂纹扩展相似,在30~400 kHz之间都有一定的能量分布,但主要集中在50~150 kHz之间[11],和R15I的谐振频率相适应。
2.2 实验系统布置
为了采集到两类声源的声波信号,采用了两种实验系统布置形式,如图3所示。图3(a)中①、②、③为R6a型传感器,30 kHz和60 kHz的标准信号经过①号传感器进入薄板传播,被②、③号传感器接收。图3(b)中④、⑤为R15I-AST型传感器,⑥为R6a型传感器。实验时分别在板面和板侧边断铅,位置紧贴④号传感器。
2.3 波形采集与分析
Fieldcal产生的两种频率的标准信号波形如图4(a)、4(b)所示。传感器③接收到的波形图如图4(c)、4(d)所示。从图中可见低频信号波经过薄板传播后,表现出较强的频散特点。符合弯曲波的特征。⑤号传感器接收到的板面及侧边信号分别见图4(e)、4(f)。
(a) 标准信号源实验图
(b) 断铅信号源实验图
图3 实验系统布置图
Fig.3 Experimental arrangement
2.4 模态辨识与声速测量
依据式(1)、式(2),计算理论波速,如果实际测量的声速符合理论值,就可判断波形属于什么模态。
2.4.1 扩展波计算
(a) 理论计算
其中取206 GPa,取7800 kg/m3,ν取0.24。
(b) 实测速度
利用图3(b)的实验布置测量声速,门槛值设定为40 dB。在0~200 μs之间的振幅较小的信号刚刚越过了门槛值,见图4(e)、4(f)。⑤号传感器记录的时间就是该波抵达时间,④号传感器记录时间作为。预触发时间内没有波形显示,所以。按照式(3)计算实际声速,计算结果见表1。从表1中可以看出,0~200 μs时间传播的声波速度与理论值基本符合,说明这种幅值低、波速快的模态波就是扩展波。而200~800 μs之间的信号有频散现象,符合弯曲波的特征。按照平板波理论,板内声源主要产生扩展波,板外声源主要产生弯曲波3。板面和板边断铅类似于这两种声源1。图4(e)、4(f)显示了板面和板侧边断铅时的波形差异,显然板内声源的扩展波幅值较大。

表1 扩展波波速

表2 弯曲波声速
2.4.2 弯曲波计算
(a) 理论计算
以30 kHz、60 kHz代入式(2)计算弯曲波的相速度。数值求解Lamb频散方程得到群速度,群速度反映波群的传播,被AE传感器接收并记录。计算数据见表2,其中。
(b) 实测声速
利用图3(a)的实验布置,按照式(3)进行群速度计算,传感器间隔分别取300、500、700 mm,结果见表2,显然,弯曲波的实测声速和理论群声速偏差较大。
3 讨论
(1) 表2中弯曲波理论群速度和实测波速有一定差别,这个差别可能是门槛值的设置过高的原因,导致实测波速比理论群速度偏小。
(2) 由于AE传感器总是垂直于板面,所以信号幅值只是薄板上质点垂直位移分量。平行板面方向的质点位移分量缺乏有效的研究手段。
(3) 和宽频断铅信号不同,单一的低频率信号经过板面传播后,没有测到较高速度的扩展波,这一点和理论不符,可能是发射的声波波列太长,和模式没法分离的原因。
4 结论
(1) 可以从传播速度上对薄板上的声波模态进行辨识。利用扩展波进行声源定位计算更加接近实际情况。
(2) 在能够屏蔽掉噪声的情况下尽可能设低门槛值,以免遗漏有效信号。
(3) 板内声源和离面声源产生的声波模态有明显差别,对裂纹信号和腐蚀信号判别可以参考这种差别。
(4) 工程实际中虽然声源位置未知,但可以选取任意传感器触发时间作为,另一传感器依据图2和式(3)计算波速,进行模态辨识。
[1] Gorman MR. Plate wave acoustic emission[J]. J. Acoust. Soc. Am, 1991, 90(1): 358-364.
[2] Dunegan HL. Modal analysis of acoustic emission signals[J].Journal of Acoustic Emission, 1998,15(1):1-4.
[3] 耿荣生,沈功田,刘时风.模态声发射基本理论[J].无损检测, 2002, 24(7): 302-306.
GENG Rongsheng, SHEN Gongtian, LIU Shifeng. A study on modal acoustic emission theory[J]. Nondestructive Testing, 2002, 24(7): 302-306.
[4] 刘晶, 陈积懋, Steve Ziole. 应用模态声发射进行自动源识别[J]. 无损检测, 2000, 22(2): 80-83.
LIU Jing, CHEN Jimao, Steve Ziole. Automated source identification using modal acoustic emission[J]. Nondestructive Testing, 2000, 22(2): 80-83.
[5] 蔡文生. 基于小波变换和模态声发射的304不锈钢点蚀声发射信号特征[J]. 石油化工设, 2013, 42(6): 21-24.
CAI Wensheng. Research on acoustice mission signals characteristic of pitting corrosion on 304 stainless steel based on wavelet transform and mode acoustice mission[J]. Petro-Chemical Equipment, 2013, 42(6): 21-24.
[6] 翟庆宏, 马长友. 金属板中的声发射波传播特性分析[J]. 炼油与化工, 2012, 23(1): 22-25.
ZHAI Qinghong, MA Changyou. Analysis on propagation characteristics of acoustic emission wave in metal plate[J]. Refining and Chemical Industry, 2012, 23(2), 22-25.
[7] 樊保圣,闫小青,扶名福等.基于Lamb波频散特性的薄板声发射源定位方法研究[J]. 固体力学学报, 2011, 32(专辑): 283-287.
FAN Baosheng, YAN Xiaoqing ,FU Mingfu, et al. Research on locating method of acoustic emission source based on the dispersive characteristic of lame wave in sheet[J]. Chinese Journal of Solid Mechanics, 2011, 32(s): 284-287.
[8] 徐凯. 超声Lamb波信号传播特性研究[D]. 南京: 南京信息工程大学, 2012.
XU Kai. Propagation characteristic research of ultrasonic lamb wave[D]. Nanjing: Nanjing University of Information Science and Technology, 2012.
[9] Karl F. Graff. Wave Motion in Elastic Solids[M]. Ohio State University Press, 1976: 245.
[10] 姚力, 赖德明. 声发射源定位不确定度的计算[J]. 无损检测, 2002, 24(11): 461-463.
YAO Li, LAI Deming. Calculation of the uncertainty of acoustic emission source location[J]. Nondestructive Testing, 2002, 24(11): 461-463.
[11] 张维刚, 黄永福, 叶荣耀, 等. 声发射检测中背景噪声对线定位精度影响研究[J]. 中国计量学院学报, 2012, 23(4): 326-331.
ZHANG Weigang, HUANG Yongfu, YE Rongyao, et al. Study on the impact of background noise on the accuracy of line localization for acoustic emission detection[J]. Journal of China University of Metrology, 2012, 23(4): 326-331.
Mode identification of guided wave and velocity measurement on a thin metal plate
ZHANG Wei-gang1, LI Kai-li1, ROUZI-Maimaiti2, HUANG Zhi-gang1, XIANG Jiang-teng1
(1. College of Quality and Safety Engineering, China JiliangUniversity,Hangzhou 310018, Zhejiang, China;2.Institute of Measurement and Quality Inspection of Kizilsu Kirghiz Autonomous Prefecture,Artux 845350, Xinjiang, China)
According to Lamb theory, guided waves contain multiple symmetric and antisymmetric modes on a plate. When the wavelength is much greater than the plate thickness, classical plate theory can be used to understand the wave motion. There are two modes of propagation. One is called the extensional (S0) and the other the flexural mode (A0). In order to research these acoustic modes, a signal source named Fedical and the other named breaking pencil lead were used for a steel plate of 0.7mm thick. Both the fundamental extensional and flexural modes were detected with transducers. Acoustic modes were analyzed and wave velocities were measured. The experimental value of the extensional wave velocity is in close agreement with the theoretical velocity, but it is difficult to measure the flexural wave velocityaccurately because of its dispersion. It can be concluded that extensional wave velocity is reliable for source localization in AE testing.
Mode Acoustic Emission(MAE); Lamb wave; wave velocity; plate wave
TG115.28
A
1000-3630(2015)-04-0322-05
10.16300/j.cnki.1000-3630.2015.04.006
2014-06-27;
2014-09-30
浙江省自然科学基金资助项目(LE15E040001)
张维刚(1971-), 男, 陕西岐山人, 硕士, 研究方向为特种设备检测与安全评定。
张维刚, zhangweigang@cjlu.edu.cn
