基于小样本的白车身尺寸偏差因素分析

赵远强

（重庆长安汽车股份有限公司工艺技术部）

由于成本原因，白车身在试生产时一般每批只生产8～10台。10台左右的样本量，远小于统计学上的最小样本量，用它评价生产线的过程能力，误差在40%以上[1]。对于小样本的处理方法，主要有Bayes方法、Bootstrap和BayesBootstrap方法及蒙特卡罗（MC）仿真方法[2]。在车身制造领域，有研究者运用Bayes方法[3-4]将车身检测数据的先验信息与小样本信息相结合，用以评估车身尺寸质量。车身焊装线设计完成时，就已经确定了其制造能力，可以将带有系统误差的测量数据进行处理，获得生产线的过程能力[5]。文章分离了造成尺寸偏差的2项构成因素，利用非随机性样式查找可归属原因，并利用随机波动数据评价焊装线过程能力。

1 检测数据处理与分析

车身焊装是一个复杂的过程，包含零件波动、人员调换、装备调整及夹具磨损等，这些因素最终耦合为测点数据的波动。

1.1 剔除奇异点

明显超出统计规律预期值的误差称为奇异点。质量控制理论中运用控制界限来监测生产过程的稳定性，判别奇异点，固有因素造成正常的波动，偶发因素造成异常的波动，这样的点一般超出控制界限，在评价过程能力时应当剔除。因为试制生产批量小，数据样本量小，所以很难判别一个偏离值较大的数据点是否由偶发因素造成。如果错误地将固有因素造成的正常波动值当作偶发因素剔除，所得到的结果就不能真实地反映制造过程能力。

文章运用比较稳健的箱线图判异法[6]对奇异点进行判定，划定小样本数据的控制界限。将原始数据按大小进行排序，找到处在数据1/4位置和3/4位置的2个数，分别称为下四分位数（QL）和上四分位数（QU）。处在中间位置的数即是中位数（ME），对于特征位置有2个数的情况，取2个数的均值作为特征数。

如果数据点（xi）符合以下条件，则可以判定为异常数据。

此方法可以更多地考虑到样本总体的情况，不受偏离值的影响，判定奇异点更为稳健可靠。在原始数据中，文章用与奇异点相邻的2个点的平均值替换奇异点数据。

1.2 分离非随机性样式

白车身试制阶段具有同批次数据之间差异小，不同批次数据之间差异大的特点，其趋势信息也随批次呈现不同的样式。文章采用简单平均法，对数据进行平滑处理。取数据本身及与其相邻的2个点，共3个点取平均值，完成1次平滑计算，得到1次平滑数据。对平滑数据再进行一次平滑迭代，得到2次平滑数据，经过三迭代，就可获得较为理想的平滑结果。平滑所得的数据就是从原始数据中分离出来的非随机性样式数据。将原始数据与平滑数据做差，即可得到随机波动数据。

分离处理得到了非随机性样式和随机数据，它们分别代表了尺寸偏差的可归属原因和过程能力2项构成因素。

1.3 查找可归属原因

非随机性样式通常是由一些特定的可归属原因造成。从原始数据中分离出非随机性样式，将有助于查找造成偏差的原因，提供整改的方向。非随机性样式有周期性样式、混合样式、平均值偏倚样式、趋势样式及系统性样式等。周期性样式是数据表现出周期性，原因是周围环境系统的变化，如温度、电压变化、作业员或机器轮调；混合样式是数据点超出或接近控制界限，而只有少数点在中心线附近，它表示的是数据来自2种不同的过程产出，例如不同的机器或操作方法不同的作业员；平均值偏倚样式是数据点向一侧偏倚，但并没有继续偏移的趋势；趋势样式是数据点向同一方向连续地移动，原因是零件的磨损及夹具的松动等；系统性样式是数据点有连续的上下跳动，常出现在黑白班交替的测量数据中。

1.4 计算过程能力指数

过程能力指数（Cp）是指过程能力满足质量标准要求的程度。一般用6倍标准差来衡量制造过程满足要求的程度。对于汽车制造，1.333＜CP＜1.667认为过程能力尚可，CP＞1.667认为过程能力充分。CP的计算式为：

式中：SUL，SLL——公差上下限；

S——标准差。

2 测点偏差构成因素分析实例

白车身测点数目有400～600个，其中影响外观或性能的测点称为关键测点，选择频繁超出公差限的少数关键测点进行分析较有针对性。测点CW125ER-LY和CW250ER-UZ的公差限为±1.5 mm，因为测量数据不理想，所以选取2个测点的3个批次数据进行分析，各10，8，12台，共30个样本。图1示出车身测点检测数据的分离处理。如图1中方形点实线所示，可以看出前2个批次的数据（前18个数据点），CW125ER-LY只有少量超出公差范围，CW250ER-UZ都在公差限内，而2个测点的第3批次数据都严重地超出公差限。

在进行奇异点剔除和进行2次平滑处理后，得到平滑数据和随机波动数据，如图1所示。3个批次的随机波动差异不大，但非随机性样式反映出数据总体变动的趋向。非随机性样式表现为平均值偏倚模型，这种偏倚可能源自于加入新员工或无经验的员工、新方法、原料（物理或化学特性的改变）、机器、环境因素（温度或污染）、检验方法的改变、检验标准的变更或是员工技能的改变。实际上，在第3批次生产前，为提升产量，增加了一批新工人，并对部分夹具进行了调整。

2个测点在滤除非随机性样式后，计算得到随机波动数据的过程能力，如表1所示。可以看出，虽然2个测点都在第3批次检测数据中表现出现了严重的超差现象，但各自的过程能力是不同的。测点CW125ER-LY的CP=1.024＜1.333，可知该过程稳定性不足，很有必要进行改进。而测点CW250ER-UZ的CP=1.773＞1.667，满足汽车制造的要求。

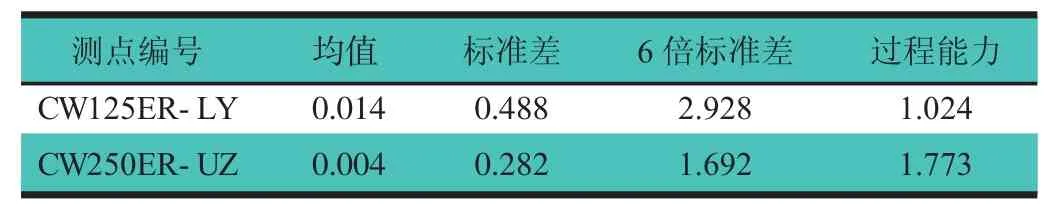
表1 车身测点随机数据的过程能力

至此，分析了造成数据超差的2项因素：可归属原因和制造过程能力。本例中，处理CW250ER-UZ时，由可归属原因造成的总体偏移，通过对公差带中值进行偏移，调整公差限去适应实测值，使测点重新回到公差范围内，经调整后稳定性较好并满足要求。测点CW125ER-LY的过程能力较差，对夹具进行分析后，发现压紧力臂的铰链处油漆掉落后，铰链松动，压紧力臂发生晃动，对零件的压紧不稳定。在更换了压紧力臂后，该测点稳定性得到提高。

3 结论

通过将检测数据进行分离分析，可以得到非随机性样式与随机波动数据。非随机性样式可以为查找可归属原因提供思路，为整改提供方向。随机波动数据可以评价焊装线的制造过程能力，预测产量提升后精度是否会下降，评定是否需要对生产线进行改进。对尺寸偏差数据的构成因素进行研究，为误差源定位及焊装误差自诊断的相关研究提供了参考。