用叠加正弦信号标定地震计的方法

林湛 崔仁胜

1）中国地震局地震预测研究所，北京市复兴路63号 100036

2）中国地震局地球物理研究所，北京市民族大学南路5号 100081

0 引言

很多地震学研究在数据处理时都要用到地震计的传递函数（洪学海等，2003；马宏生等，2007；周连庆等，2008；裴顺平等，2010）。地震计的实测传递函数是用参数待定的模型拟合实测幅频响应而得到的（Levy，1959；Sanathanan et al，1963；王广福，1984）。因此，在计算传递函数前进行幅频响应测试是必不可少的；并且，地震计用户可通过幅频响应来判断地震计运行状态是否正常。故幅频响应测试对地震台网的运维工作非常重要。

电测法是进行幅频响应测试的常用方法。测试时，某种形式的激励电流被输入到地震计的标定线圈内，地震计的输出端会产生响应电压，我们可通过分析输出电压和输入电流之间的关系得到幅频响应（Bormann，2002）。

目前，国内的地震计使用者通常采用正弦标定方法测试幅频响应（Murphy et al，1954；Willmore，1959；林湛等，2008；邵玉平等，2008；刘明辉等，2014）。测试时，频率不同的正弦激励信号被依次输入。由于不同频率的激励信号之间须留有间隔，而且每个频率的响应信号头部都会有瞬态响应；所以，在整个响应信号中，只有一部分能被用来分析，数据可用率较低。另外，数据处理时需找到每个频率的正弦响应，并在其中找到稳态响应；所以正弦标定不易实现自动处理。

本文介绍了用叠加正弦信号标定地震计的方法（简称叠加正弦标定）。测试时，我们将不同频率的正弦信号叠加在一起作为激励信号，因而响应信号是连续的，且瞬态响应仅出现在整个响应信号的开始部分。因此，几乎整个响应信号都能被用来分析，数据可用率较高。数据处理时，只需避开整个响应信号开始部分的瞬态响应，因此叠加正弦标定容易实现自动处理。通过地震计幅频响应测试实验发现，该方法测试的相对误差小于1%。

本文首先介绍了电测法标定的一般原理以及正弦标定响应中的瞬态响应、稳态响应，从而引出了正弦标定应用中存在的问题；然后介绍了叠加正弦标定的原理、实验步骤和数据处理方法；最后介绍了一个具体的叠加正弦标定实验并将叠加正弦标定与正弦标定进行了对比。

1 电测法标定

首先简单介绍一下电测法标定。图1为电测法标定的原理图。测试时，激励电流i（t）被输入到地震计的标定线圈中，地震计会输出响应电压u（t）。通过分析响应电压和激励电流之间的关系，我们可以得到地震计的幅频响应等特性。为了将响应电压记录下来，我们将其输入到数据采集器（简称数采）中。数据采集器会对响应电压进行采样和量化，输出记录数据d（n）。

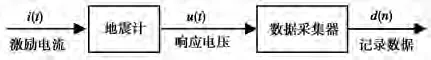
图1 电测法标定示意图

2 正弦标定响应中的瞬态响应和稳态响应

正弦标定是激励电流为正弦电流的电测法标定。我们假设激励电流的表达式如下

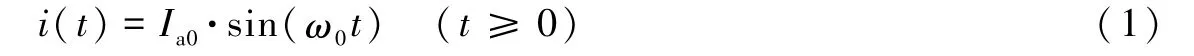
式中，i（t）为激励电流；t为时间；Ia0和ω0分别为正弦电流的幅度、角频率。激励电流在t=0时接入，频率f0与角频率ω0的关系为

对式（1）等号两边进行拉普拉斯变换得到

式中，s为拉普拉斯算子。根据地震计的设计原理，得到（林湛等，2015）

式中，H（s）为地震计的传递函数（传递函数指的是将振动速度作为输入且将电压作为输出时的传递函数）；I（s）、U（s）分别为电测法标定时激励电流i（t）、响应电压u（t）的拉普拉斯变换；G为地震计的标定常数，其单位是m·s-2/A。将式（3）代入式（4）并整理后得

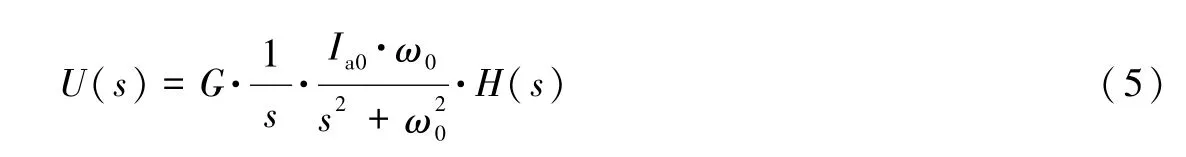
下面，计算U（s）的拉普拉斯逆变换u（t）。首先，将U（s）分解为（郑君里等，2000）

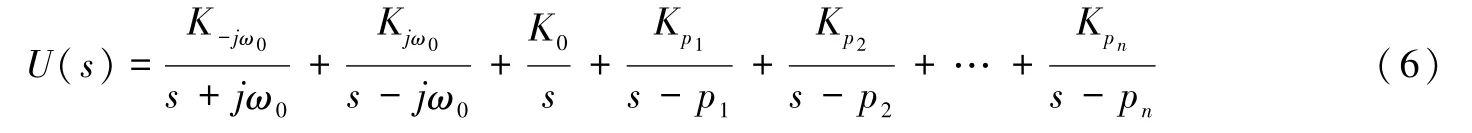
式中，j为虚数单位；p1，p2，…，pn为H（s）的极点为部分分式分解各项的系数。系数和K0的求解过程如下：

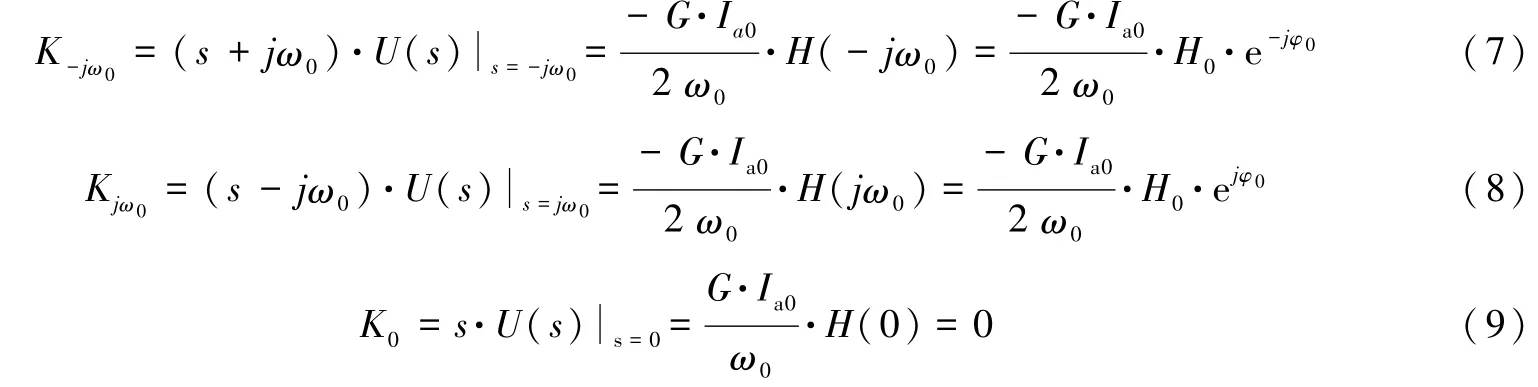
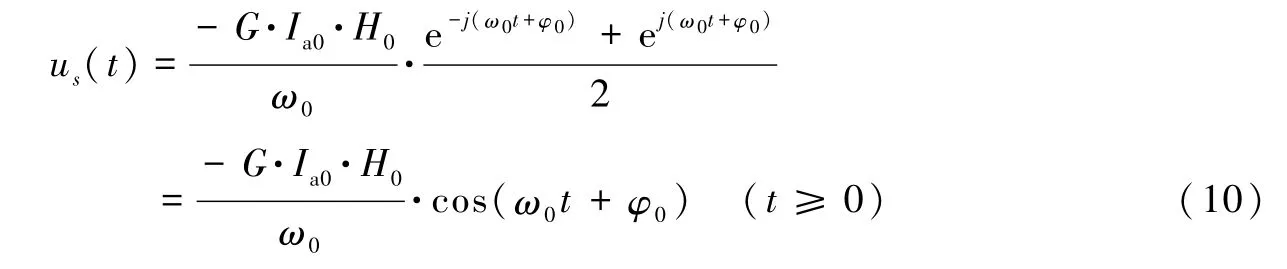
最后，求解式（6）所有项的逆变换，结果为

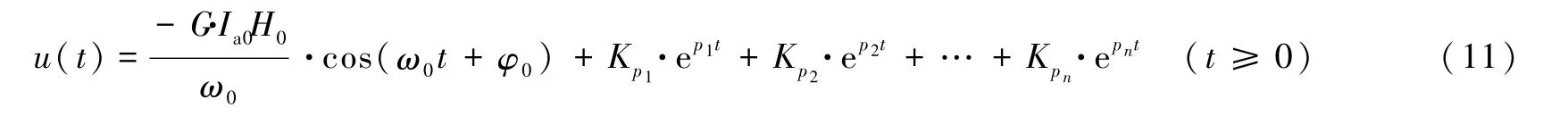
对于稳定系统，p1，p2，…，pn的实部必小于零。式（11）中的各指数项，当t趋于无穷时都趋于零，是瞬态响应。式（11）中的第1项（即us（t）项）是稳态响应。令稳态响应的幅度为Ua0，则式（10）可重写为

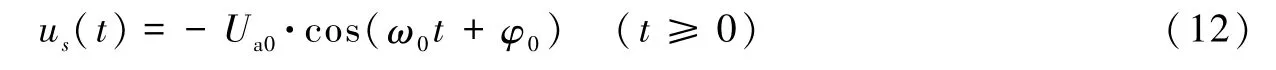
通过对比式（10）、（12），可以看到幅频响应H0可由

计算，式（13）即正弦标定数据处理的公式。数据处理时，Ua0可通过数据处理得到，Ia0、ω0为已知，G可从地震计参数表上查到。图2为1次正弦标定测试中记录的响应电压。在这次测试中，正弦激励电流的频率为0.05、0.10、1.00Hz，被测地震计的周期为120s。从图2可见，每个频率的正弦响应电压在开始时都有跳跃现象，这种跳跃现象是瞬态响应的表现。在经过大约120s后，瞬态响应基本消失，稳态响应依然存在，在进行数据处理时应测量稳态响应电压的幅度。

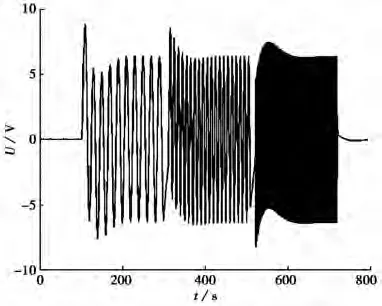
图2 一次正弦标定测试中记录的响应电压

3 正弦标定应用中存在的问题

3.1 数据的可用率低

每个频率的正弦响应开始时都包含明显的瞬态响应分量。而地震计的周期越长，瞬态响应持续的时间也越长（此处，瞬态响应持续的时间指响应中包含明显瞬态响应分量的时间）；测试的频点越多，瞬态响应出现的次数也越多。在数据的时间长度一定的情况下，瞬态响应所占的时间长度越长，稳态响应所占的时间长度就越短。也就是说，可用于数据处理的数据越短，数据的可用率越低。而且，不同频率的响应信号之间的间隔也会挤占可用数据的时间，使数据的可用率降低。

3.2 不易实现自动处理

数据处理时需要找到每个频率的正弦响应，并在其中找到稳态响应。一般情况下，这项工作需要人工完成。有时，可根据预设的每个频率激励电流的持续时间及不同频率激励电流的间隔时间来实现自动查找。但是，有些数据采集器在发送激励电流时不能保证间隔时间为固定值。

4 叠加正弦标定的原理

为解决正弦标定应用中存在的问题，我们引入了叠加正弦标定。在进行叠加正弦标定时，激励电流是Q个正弦电流的叠加，其表达式为

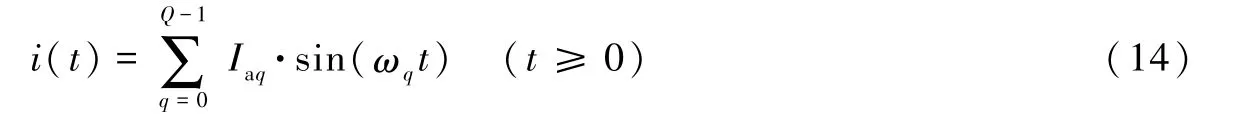
式中，i（t）为激励电流；t为时间；Iaq、ωq分别为第q个正弦电流的幅度和角频率。激励电流在t=0时接入。由于地震计为线性系统，所以在叠加正弦电流激励下产生的响应是在单个正弦电流激励下产生的响应的叠加。因此，在进行叠加正弦标定时，瞬态响应只在全响应的开始部分出现一次，而稳态响应的表达式为

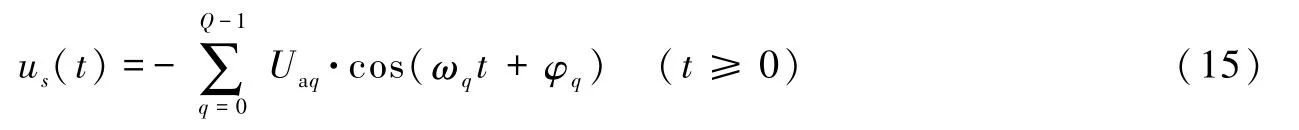
式中，us（t）为模拟信号，它经数采采样后，形成数字信号（或序列）ds（n），ds（n）的表达式为

Ts为采样周期；n取大于或等于0的整数；式（15）、（16）中Daq与Uaq的关系为

式中，Kdig为数采的转换因子，单位是V/count。

在进行数据处理时，被处理的数据只能是有限长度的序列。此处，我们假设被处理的数据是ds（n）的前N个数，记为x（n）。为了方便表述，本文中我们称x（n）为叠加正弦标定波形数据，x（n）的表达式为

数据处理的步骤如下：①利用离散傅里叶变换（DFT）对x（n）进行处理，得到每个频点的Daq；②以式（17）计算每个频点的Uaq；③以式（13）计算每个频点的幅频响应Hq。步骤②、③比较简单，步骤①比较复杂。下面，我们详细研究步骤①。为了计算叠加正弦标定波形数据x（n）的离散傅里叶变换，首先计算x（n）的一个分量的离散傅里叶变换，然后利用离散傅里叶变换的叠加性（线性），得到x（n）的离散傅里叶变换。

4.1 叠加正弦标定波形数据的一个分量的离散傅里叶变换

叠加正弦标定波形数据x（n）的一个分量x0（n）的表达式为

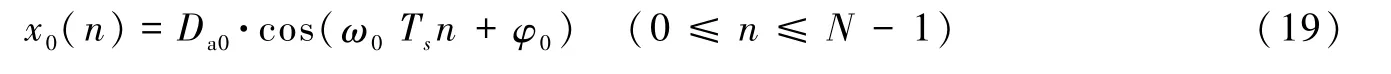
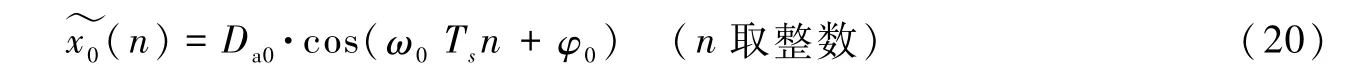
若采用本文介绍的数据处理方法，x0（n）须满足2个要求：①x0（n）的扩展序列为周期序列；②x0（n）的长度为其扩展序列的周期的整数倍。

假设x0（n）的长度的周期M0的L0倍，则

根据离散傅里叶变换的定义，x0（n）的离散傅里叶变换X0（k）的表达式为

利用欧拉公式，式（23）可写成

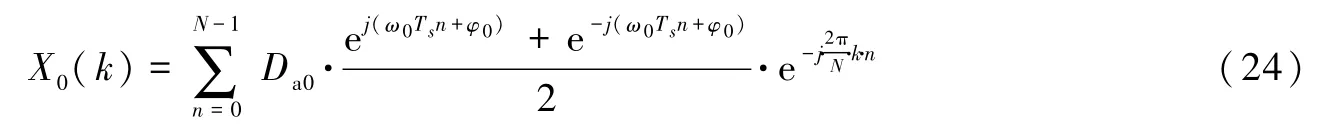
对式（24）进行整理可得

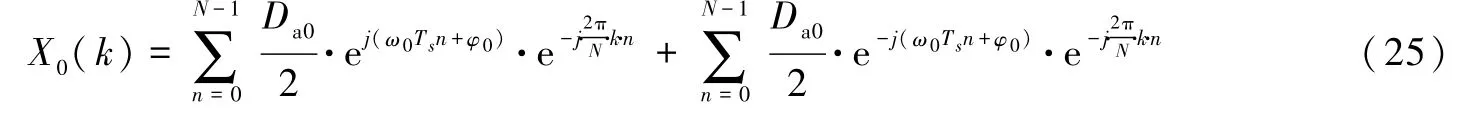
令式（25）等号右边第 1项为Y0（k），第 2项为Z0（k）。 则式（25）可写成

下面，首先计算Y0（k），然后计算Z0（k），最后将两者结果相加得到X0（k）。Y0（k）可整理为

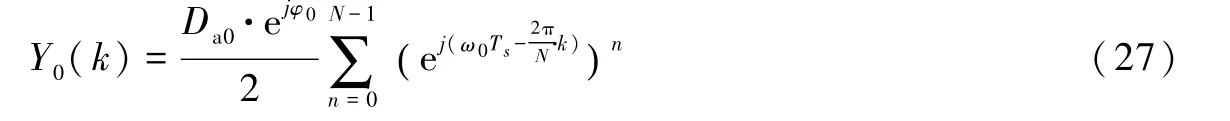
下面根据k的取值不同，分2种情况计算Y0（k）。

情况1：

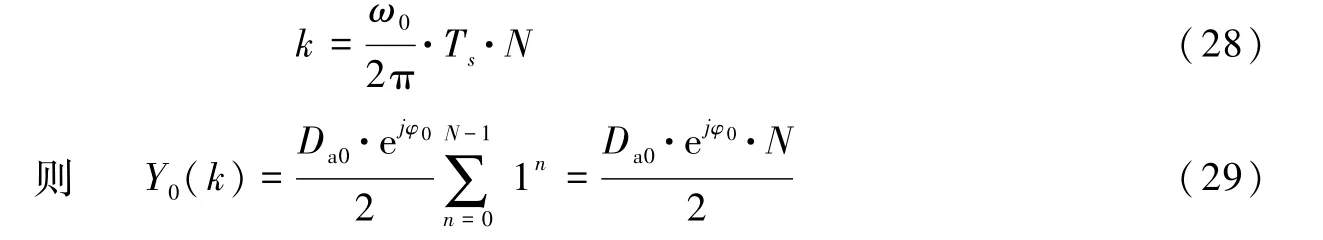
情况2：k取其它值

由等比数列求和公式可得

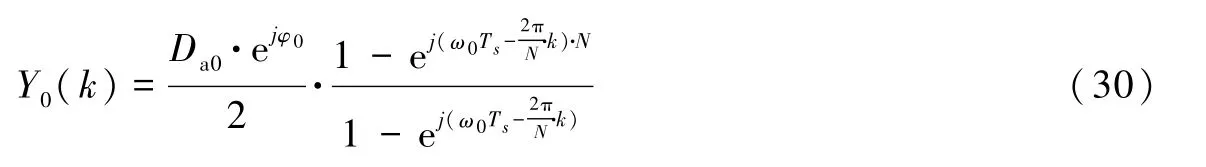
由式（21）可得

将式（31）代入式（30）得

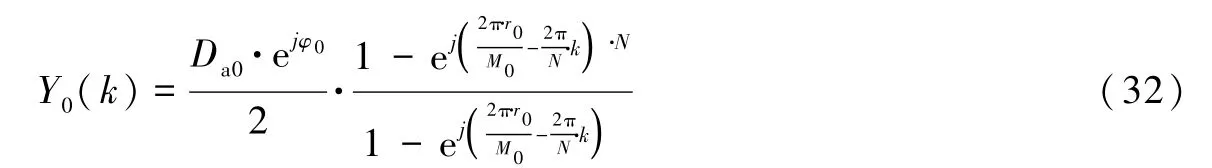
将式（22）代入式（32）并整理得

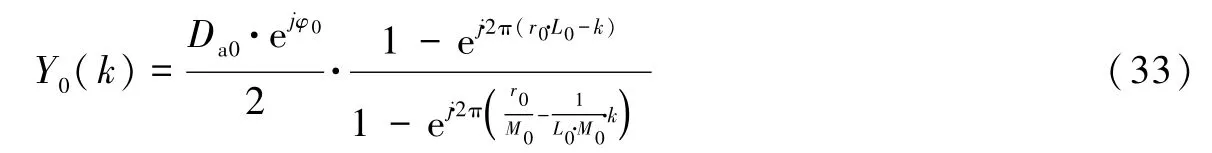
由于r0、L0、k都是整数，所以

综合情况1和情况2可得

从目前情况看，公司主要依靠技术熟练、忠诚可靠的员工建立和维持这样良好的声誉。当行业内许多小公司选择技术导向的竞争战略时，公司选择了不同的方法。公司现在的管理政策侧重于劳动密集战略，主要依靠拥有的劳动力，而不是最新的技术。公司过去5年的销售和利润，见表1所示。行业内销售收入和利润的环比增长率分别为15%和10%。很显然，公司的销售收入和利润的环比增长率低于行业水平，这始终困扰着管理层。

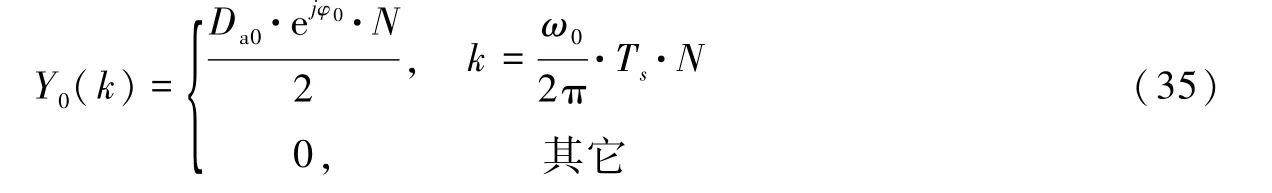
用同样的方法可计算Z0（k），即

由于X0（k）=Y0（k）＋Z0（k），所以

由于x0（n）是实序列，X0（k）具有对称性。所以，在计算与k对应的模拟角频率ω时，我们只考虑的情况（也就是说的情况不在考虑范围之内）。下式为计算与k对应的模拟角频率ω的公式，即

通过以上论述，可得到如下结论：当x0（n）的扩展序列为周期序列并且x0（n）的长度是其扩展序列的周期的整数倍时，在区间内，X0（k）只在模拟角频率ω0对应的k处取值为在其它处取值为0。

4.2 叠加正弦标定波形数据的离散傅里叶变换

现将叠加正弦标定波形数据x（n）重写为

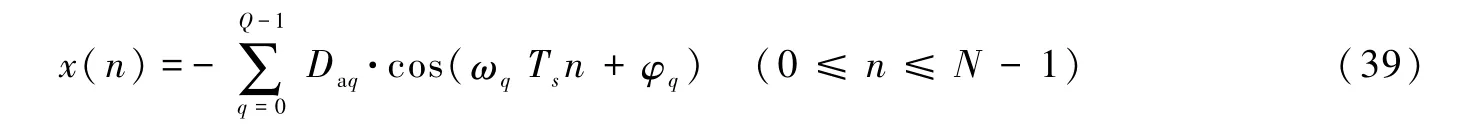
通过选择激励电流信号中不同正弦分量的角频率（利用式（21）），我们可使x（n）各个分量的扩展序列为周期序列且使

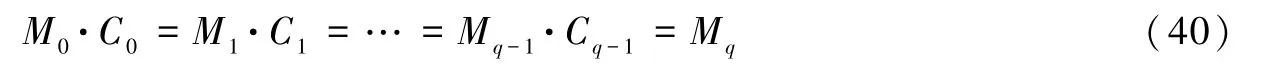
成立，式中，M0，M1，…，Mq-1，Mq为x（n）各个分量的扩展序列的周期，并且M0≤M1≤ … ≤Mq-1≤Mq。C0，C1，…，Cq-1为正整数。通过选择数采记录数据中用于处理的数据的长度，我们可使x（n）的长度N为Mq的整数倍，即

也就是说，N为M0，M1，…，Mq-1，Mq的整数倍。这样，x（n）的各个分量都满足 4.1节中对数据的2个要求。x（n）

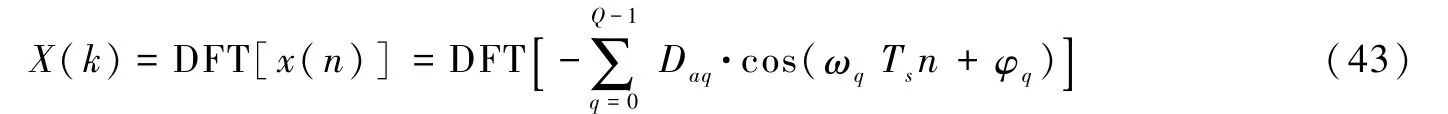
的离散傅里叶变换为

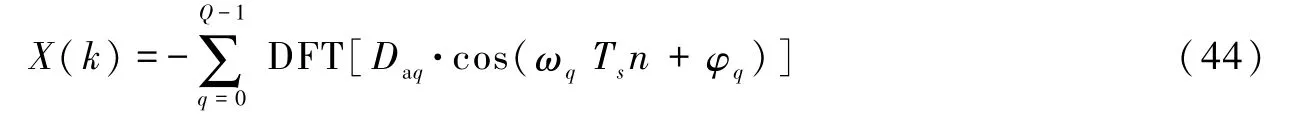
由离散傅里叶变换的叠加性可得由式（44）和4.1节中的结论，可得如下结论：当x（n）各个分量的扩展序列为周期序列且式（40）、（41）中的关系成立时区间内，X（k）在模拟角频率ω0，ω1，…，ωq对应的k处 取 值在其它处取值为 0。 在得到我们可由

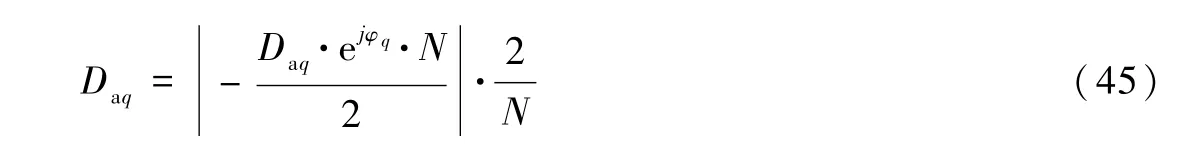
计算Daq。

5 叠加正弦标定的实验步骤和数据处理方法

5.1 实验步骤

（1）设计激励电流信号。利用式（21）选择激励电流信号中不同正弦分量的角频率，使式（40）中的关系成立。

（2）产生激励电流信号。设置任意波形信号发生器，使其产生步骤（1）中设计的激励电流信号，并将激励电流信号加在地震计的标定线圈上。

（3）用数据采集器记录地震计的响应电压信号。用于处理的数据应避开最开始的瞬态响应，数据长度应符合式（41）。

5.2 数据处理方法

（1）用式（43）、（45）对数据进行处理并计算，得到每个频点的Daq。（如果数采记录数据较长，可设置一个滑动窗口。窗口长度应符合式（41）。窗口每滑动一步，就用式（43）、（45）对窗口中的数据进行处理并计算，得到Daq的一个中间结果。Daq的最终结果是多个中间结果的中位数。）

（2）用式（17）计算每个频点的Uaq。

（3）用式（13）计算每个频点的幅频响应Hq。

6 叠加正弦标定与正弦标定的对比

首先，我们采用叠加正弦标定和正弦标定2种测试方法对同一台地震计进行测试，对结果进行对比。然后，对这2种方法的数据可用率的高低和实现数据自动处理的难易程度进行对比。

该测试实验分为低频和高频2个子实验。通过2个子实验，可分别测试地震计低频段和高频段的幅频响应。在进行叠加正弦标定时，选用的参数见表1。被测地震计为 Posthole120型浅井宽频带地震计。Posthole120型地震计的频带宽度为0.008333～100Hz，灵敏度为 2000V/（m/s）。

首先，我们对同一台地震计进行多次叠加正弦标定，以检验该方法测试结果的一致性。图3、4分别为低频段、高频段10次标定的结果。（由图3、4可见，10条线几乎重合。这说明该方法的测试结果具有很强的一致性。

表1 进行叠加正弦标定时选用的参数

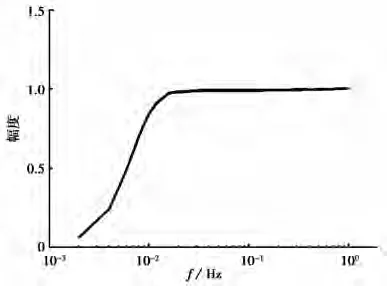
图3 低频段10次叠加正弦标定的结果

图4 高频段10次叠加正弦标定的结果

我们再对同一台地震计进行正弦标定，然后将其结果与前面的多次叠加正弦标定的结果进行对比，以检验这2种方法测试结果的一致性。在图3、4的结果中分别添加正弦标定的结果得到图5、6。图5、6中，实线为叠加正弦标定的测试结果，圆点为正弦标定的测试结果。由图可见，圆点几乎都落在实线上。

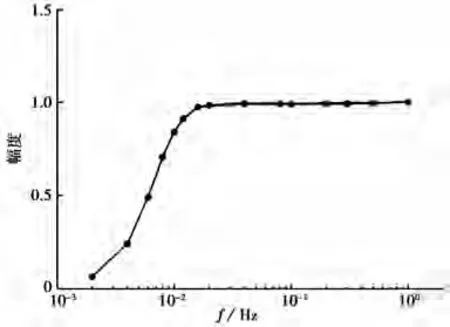
图5 低频段叠加正弦标定结果与正弦标定结果的对比

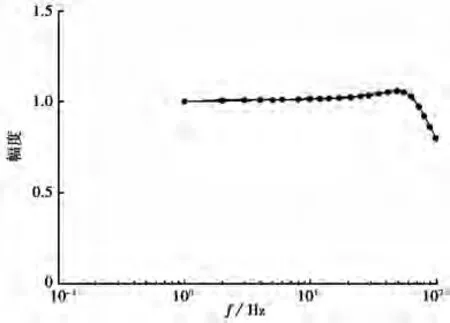
图6 高频段叠加正弦标定结果与正弦标定结果的对比

在统计学中，我们通常用相对误差来衡量测试结果的准确度。相对误差的定义如下

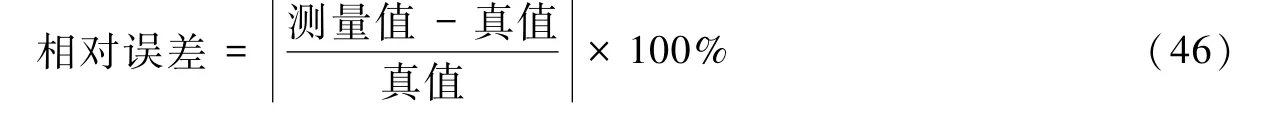
正弦信号的能量只集中在某一频点，在对某一频点的测试中可达到很高的信噪比。因此，可将多次（例如10次）正弦标定结果的平均值作为地震计幅频响应的真值。此处，我们将叠加正弦标定测试结果作为测量值。通过计算，各次叠加正弦标定结果的相对误差均小于1%。

我们可以把叠加正弦标定的低频段、高频段测试结果拼接起来，得到全频带上的幅频响应，结果如图7所示。由图可见，被测地震计通频带内的幅度响应是比较平坦的，低频和高频截止频率分别为0.008333、100Hz。

通过对正弦标定和叠加正弦标定2种方法数据可用率的高低及实现数据自动处理的难易程度进行对比后发现：

（1）正弦标定时，不同频率的响应信号之间有间隔，而且每个频率的响应信号的开始部分都会有瞬态响应，数据可用率较低；叠加正弦标定时，响应信号是连续的，而且瞬态响应只在整个响应信号的开始部分出现一次，数据可用率较高。

（2）对正弦标定的数据进行处理时，需找到每个频率的响应，并在其中找到稳态响应，正弦标定不易实现数据自动处理；对叠加正弦标定的数据进行处理时，只需避开整个响应信号开始部分的瞬态响应，叠加正弦标定容易实现数据自动处理。

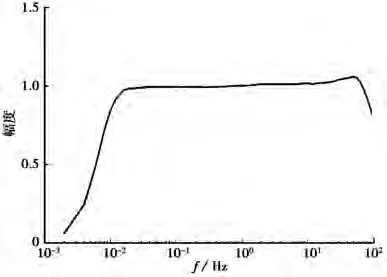
图7 叠加正弦标定低频段和高频段测试结果的拼接

7 结语

本文介绍了利用叠加正弦信号标定地震计的方法。与正弦标定相比，叠加正弦标定的数据可用率更高，而且更易实现数据自动处理。通过对地震计幅频响应的测试实验发现，采用叠加正弦信号测试时，相对误差小于1%。该方法的应用有助于提高地震台网仪器检测工作的自动化程度，使台网维护工作更加高效。