利用余震能量场进行宏观震中快速判定的研究

2015-09-03郑韵姜立新杨天青刘杰

中国地震 2015年4期

郑韵姜立新杨天青刘杰

1）中国地震局地震预测研究所，北京市复兴路63号 100036

2）中国地震台网中心，北京 100045

0 引言

破坏性地震发生后，地震烈度等震线图可以直观明了地显示地震的影响范围、灾害分布面积和各个灾区的受灾程度等，因此地震烈度快速判定是应急救灾中十分重要的组成部分。目前，基于经验关系的烈度快速判定还存在很多问题，微观震中和宏观震中的偏离是其中最主要的缺陷之一。微观震中是地震破裂的初始点在地表的投影，并不一定是地震破裂最大地区的中心；而宏观震中是极震区的几何中心，两者之间可能存在偏离。只有从震源区中心开始的对称破裂型地震，两者才较为吻合。一般来说，地震震级越大，破裂尺度也越大，两者间的偏离也可能随之增大。

由于地震发生的初期无法迅速获得宏观震中的位置，现行的烈度快速判定中通常将速报震中（微观震中）作为初始输入参数，这直接影响了极震区位置的判定以及后续的抗震救灾工作，因此，提高快速评估中宏观震中的精度成为亟待解决的问题。大地震后断层面的应力发生调整，从而触发了余震（Gomberg et al，1997；Kilb et al，2000；吴小平等，2008）。这些余震，特别是主震后短时间内发生的余震包含了主震震源区的丰富信息，并且与主震的破裂过程密切相关。近年来，中国学者开始探讨余震信息在震后应急工作中的应用问题。白仙富等（2011）对1966年以来云南地区22个MS≥6.0震例影响场和余震序列的空间关联度进行统计分析，认为用一元线性回归反演宏观震中和影响场较为理想；王伟锞等（2011）通过对1970年以来近40组破坏性地震的研究，提出了利用震后6h余震质心推断宏观震中的方法；张苏平等（2013）探讨了余震信息在漳县岷县6.6级地震后对于重灾区快速判定的作用；杨天青等（2015）利用震级加权标准差椭圆法研究了基于震后短期内（24h）余震序列判定地震极灾区的方法。上述研究对于震后快速评估有一定意义，但这仅是对于早期余震空间分布的简单统计。郑韵等（2015）提出了用余震频度法估计极震区和宏观震中，尝试将余震影响弥散至空间，结果似乎展现出更为丰富的震兆信息。本文进一步将震级权重主要是余震能量指标纳入极震区判定中，从而探讨一种可以有效估计宏观震中的方法。本文主要以汶川地震为例说明完整性震级确定的步骤和结果，余震能量场计算方法和能量场分布图的绘制以及宏观震中的确定，最后将选取的7次大地震震后每个时段估计震中和实际宏观震中进行比较和分析。

1 数据和方法

1.1 数据

计算地震频度N值所用资料来自中国地震台网中心地震目录。本文选取震例的原则如下：①我国西部1970年以来MS≥6.5的破坏性大地震；②震例实际影响场是经过实际现场震害调查确定的，删除由于地质条件、气候或人烟稀少等因素无法进行极震区烈度现场调查的震例；③地震序列为主震型，即主震释放能量占全序列的90%以上，此时地震破坏程度的大小主要受主震的影响；④主震后24h内余震序列频次n≥50，余震活动水平较高，频度统计更为可靠。选取的7次大地震如表1所示，对这7次地震序列24h内余震记录进行计算。需要说明的是，为了研究的一致性，1次地震只取1次宏观震中，我们将汶川地震的宏观震中取为Ⅹ度区的几何中心。

1.2 确定完整性震级

作为描述地震活动性的基本关系，G-R定律（Ishimoto et al，1939；Gutenberg et al，1944）描绘了地震的发生频度和震级之间的指数关系

式中，M为震级；N为震级大于等于M的累计频度；a、b为常数。采用式（1）可以确定余震的完整性震级。

1.2.1 确定最小完整性震级

最小完整性震级作为地震活动性研究的重要影响因素，是地震目录品质的体现。只有正确估计最小完整性震级才能得到可靠的地震活动性参数。我们利用Wiemer等（2000）提出的拟合效果测试法估计区域最小完整性震级及其时空分布，其基本原理是根据G-R关系的幂指分布来拟合真实的震级-频度分布。拟合效果测试法给定拟合优度评价函数R，不断调整起算震级，当拟合结果达到该标准，即可将该起算震级作为最小完整性震级Mc。

拟合优度评价函数R

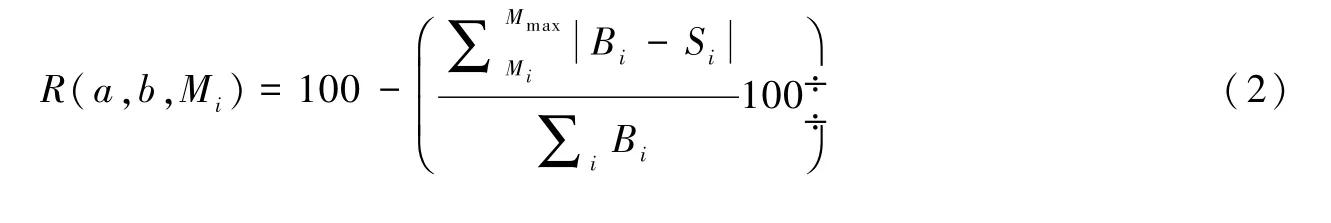
式中，Bi为观测震级档的累计频度；Si为估计震级档的累计频度；Mi为起算震级。

1.2.2 确定最大完整性震级

当拟合优度达到最佳之后，随着Mi的增加，R值逐渐下降。这是因为震级-频度关系线性度较好的小震级段逐步被舍弃，较高震级段一些震级档的缺震，使得幂指分布拟合震级-频度关系的可靠性下降。为此，我们提出了“最大完整性震级”的概念。其基本原理仍是根据G-R关系的幂指分布来拟合真实的震级-频度分布。同样，我们利用拟合优度评价函数R进行拟合效果测试，将最佳拟合优度之后的第1个R＜85%对应的前一个Mi定义为最大完整性震级。

本文采用最小二乘法计算b、a值，以0.1作为调整震级，拟合优度取至少85%，即所得到的G-R关系可以解释85%的观测数据。另外，每个震例只取24h内余震最大完整性震级为该地震上限震级。

1.3 计算余震能量场

地震波从破裂面上一个破裂单元向外传播，离能量释放处愈远，地震波能量或振幅会愈小，即所谓衰减。因此，某点在一段时间内接受的地震能量应是这段时间内周围所有地震波传播至该点的能量之和。

表2 汶川地震震后各时段完整性震级

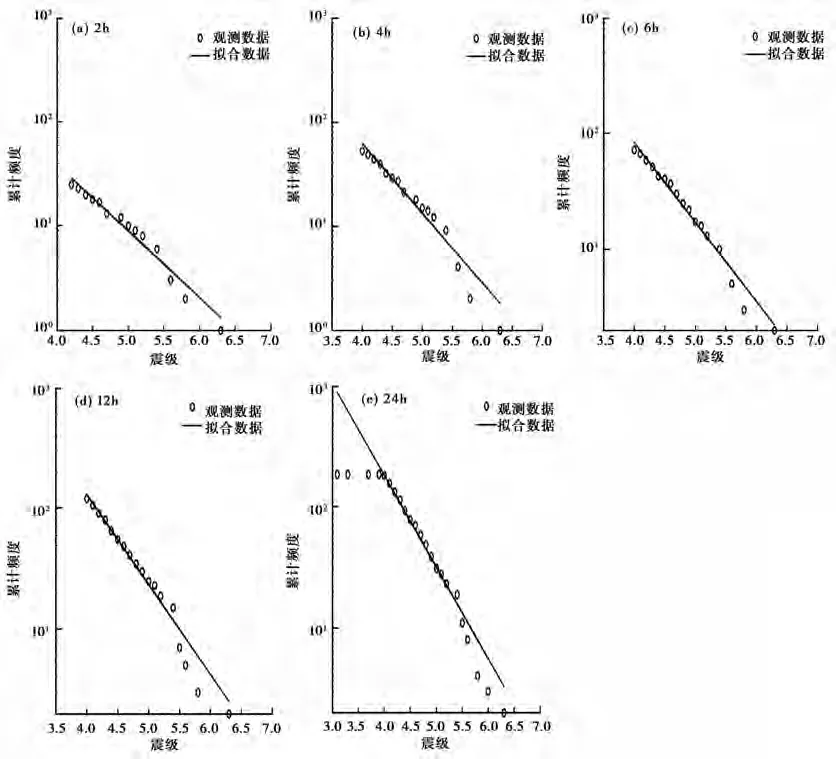
图1 汶川地震震后不同时段的M c作为起算震级获得的震级-频度、拟合G-R关系的分布

由于地球介质和震源过程的极端复杂性，故进行如下简化假设：将均匀介质半无限空间的表面震源看成点源，其弹性波能量沿直射线传播，并且耗损仅按e-kr形式吸收。在距离震源r处单位表面的能量为（傅淑芳等，1980）

E0为该地震的能量；k取平均值0.0003km（刘正荣，1977）。一般情况下，能量源不能假设为固定的点源（Sarma，1977），但是当震源尺度较小并令能量作球形辐射时，则可近似为点源。

将研究区以0.01°为节点的间隔进行网格化，某段时间内第（i，j）节点处经历的地震能量是期间所有m个地震在（i，j）处能量之和，即

式中，En为第n个地震的能量；rij为第n个地震到（i，j）节点的距离。能量的计算采用关系式：logE=11.8＋1.5MS（Gutenberg et al，1942）。中国地震台网中小地震目录通常采用里氏震级ML，ML、MS由公式MS=1.13ML-1.08④郭履灿，1971，华北地区的地方性震级M L和面波震级M S经验关系，见：全国地震工作会议资料，1～10。进行转换。

1.4 绘制余震能量场

将研究区以0.01°为节点的间隔进行网格化，采用的起始震级为最小完整性震级，上限震级取最大完整性震级，其因有二：①能量主要集中于较大地震，震后24h内的强余震是个别现象，它将导致极端不均匀的能量分布，并将严重影响极震区判定的准确性进而影响宏观震中判定的准确性；②余震能量场计算时将震源作了点源假设，但强余震近场不适合近似为点源。如1.3所述计算每个节点的能量值，最后，由所获取的全部节点能量值绘制其空间分布等值线图。

1.5 判定宏观震中

地震极震区是指遭受地震灾害直接损失最严重的区域，不包括对社会经济无影响的地震地质灾害区（袁一凡，2011）。极震区通过震后烈度调查评估确定，是地震烈度图中最内圈的烈度等震线，其几何中心就是宏观震中。而仪器震中是主震破裂的起始点，两者之间通常存在一定偏差。主震发生后，发震断层面上的应力瞬间出现调整，从而触发了余震。余震发生需要一个时间过程，既不是全部同时发生，也不一定均匀地散落在主震震源区。因为强余震发生的地区可能是破坏更严重的区域，所以我们将不同主震震级分别对应不同余震震级范围进行极震区的估计。

经过对本文所取7次地震的研究发现，宏观震中的估计分为2种情况：

（1）主震对应震级的余震集中分布于一个高能量区，取最内包含主轴方向所有对应震级余震能量等值线区域为估计极震区。以2013年4月20日芦山7.0级地震为例，估计极灾区为最内圈包含所有ML≥3.5余震能量等值线范围。利用ArcGIS（美国环境系统研究所研发的地理信息系统平台产品）数字化提取极震区并计算中心坐标，即估计宏观震中。图2为ArcGIS数字化估计震中方法1示意图。

（2）主震对应震级的余震大部分位于一个高能量区，个别散落在余震高能量区之外。取最内包含所有主轴方向对应余震能量等值线中心为估计极震区长轴的一端，将零星对应余震中心定为长轴的另一端，两者连线的中点即为估计宏观震中。以2010年4月14日玉树7.1级地震为例，极震区长轴一端是最内圈包含所有ML≥3.5余震等值线中心，另一端是零散的ML≥3.5余震中心。图3为ArcGIS数字化估计震中方法2示意图。

设x1、x2、…xn为已知密集区外零星余震的经度，y1、y2、…yn为零星余震的纬度。xcen为这些余震中心的经度，ycen为这些余震中心的纬度。则

表3 估计极震区震级对应表

图2 ArcGIS数字化估计震中方法1示意图

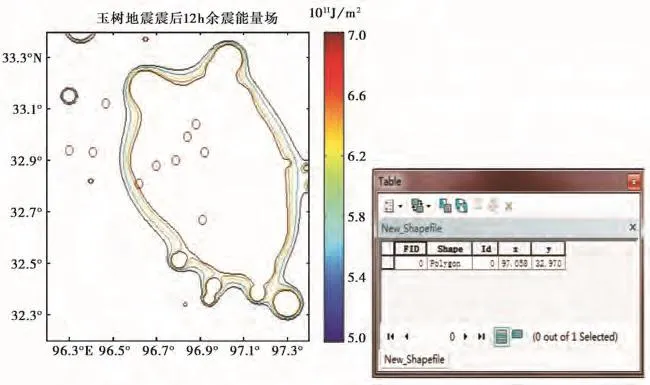
图3 ArcGIS数字化估计震中方法2示意图

2 结果

2.1 能量场分布图

图4为2008年5月12日汶川8.0级地震震后2、4、6、12、24h等5个时间段的余震能量场和估计宏观震中。由图4可见，汶川地震估计震中属于第1类，即ML≥4.0余震集中展布于一个高能量区，估计极震区为图4中深红色区域，估计震中为黑色五角星。

图4 汶川地震震后5个时段余震能量场分布图和估计宏观震中

汶川地震震后2h内余震高能量区基本为汶川地震烈度的Ⅹ度区，反映了震源破裂区可能包含北川-青川一带，此时估计震中在宏观震中西南向约40km处；震后4h余震高能量区覆盖了汶川地震烈度Ⅸ度区的大部分，能量释放范围有所扩展，基本可以确定主震破裂区包括了汶川-北川-青川沿线；震后6h青川地区的余震释放能量逐渐累积，主要能量释放区沿汶川-北川-青川地区呈明显的条带状分布，此时估计震中比较接近宏观震中；震后12h余震高能量区分布在汶川、青川地区，面积继续扩大，并且汶川地区能量释放水平略高于青川地区；震后24h余震高能量区覆盖了汶川地震重灾区的大部分地区，高能量区尺度范围大约350km，比张勇（2008）通过地震波形资料反演得到的310km破裂尺度长一些，也就是说震后24h内的能量主要释放区域大体反应了汶川地震破裂尺度的大小和极灾区的面积，估计震中位于宏观震中偏东北一些。

汶川大地震的震源过程错综复杂：从破裂开始到震后12s，破裂主要表现为双侧破裂形式，即同时向东北和西南2个方向扩展；震后16～30s，震中东北方向约80km处开始新的破裂，并快速向西南方向传播；震后30～42s，震中东北和西南方向都有一些零星的破裂；震后48～58s，北川和康定附近下方发生破裂；震后60s以后，主要是震中东北发生一些小破裂（张勇，2008）。对于这么复杂的破裂过程，余震的时空分布相应地与其它地震余震有所不同，东北段北川-平武地区的余震发生时间晚于西南段汶川-都江堰地区，余震密度也低于西南段，这与汶川地震的震源破裂过程应该有一定关联。并且由震后4h余震高能量释放区推断震源破裂区包含青川地区，估计震中已经能大致反映出汶川地震的宏观震中，震后6h以后高能量空间覆盖尺度略有扩张，估计震中位置越来越靠近宏观震中。震后24h高能量空间展布区较好地反映了汶川地震震源区的破裂尺度，这也是汶川地震破坏最严重的地区。

2.2 结果分析

图5为炉霍地震、大关地震、玉树地震、芦山地震、漳县岷县地震以及鲁甸地震等6次破坏性地震震后24h余震能量场分布和估计震中。由图5可见，除玉树地震外，其它5次地震均属于估计震中的第1类，即对应震级余震集中分布于同一高能量区，它们的估计极灾区为图中的深红色部分，估计宏观震中为图中黑色五角星所示位置；玉树地震属于估计震中的第2类，ML≥3.5余震部分位于一个高能量区，个别ML≥3.5余震散落于高能量区外，图中蓝绿色线段为估计极灾区长轴，估计宏观震中亦以黑色五角星表示。

一般来说浅源大地震用矩形或椭圆形位错面模拟。芦山地震、漳县岷县地震震后24h内的余震基本分布在主震震源区且大体上为椭圆型的区域内，余震能量场以类椭圆状向外逐渐衰减。大关地震、鲁甸地震余震能量场均有2个较为明显的优势方向，据此可以推测它们很可能为共轭破裂地震。玉树地震余震能量场展示出余震主要分布在震中东南方向上，余震区更加狭长且与主震震中有一定距离。原因可能是玉树地震的破裂传播是一个由缓到急的过程，破裂从初始点开始主要向东南方向扩展，由“地震多普勒效应”导致东南方向上产生强烈能量聚集，这也是玉树城区之所以遭受严重灾害在震源方面的主要原因（张勇等，2010）。由于炉霍地震余震定位精度很差，暂不作分析。

第1类估计震中地震的破裂可能主要发生在断层面上靠震源附近，没有明显的破裂方向，如芦山地震（张勇等，2013）；也可能朝某些方向（单侧或双侧）破裂传播，甚至是共轭断层发生破裂，但存在破裂优势方向，如汶川地震、漳县岷县地震、鲁甸地震（张勇，2008；刘成利等，2015；张勇等，2014）。第2类估计震中的地震总体上倾向于是单侧破裂事件，但包含2次子事件，后半段子事件破裂速度快于前半段（张勇等，2010），这导致后半段断层面库仑破裂应力变化更显著，进而触发了大量余震。7次地震各时段估计震中、微观震中与宏观震中的距离如表4所示。

图5 6次地震震后24h余震能量场分布

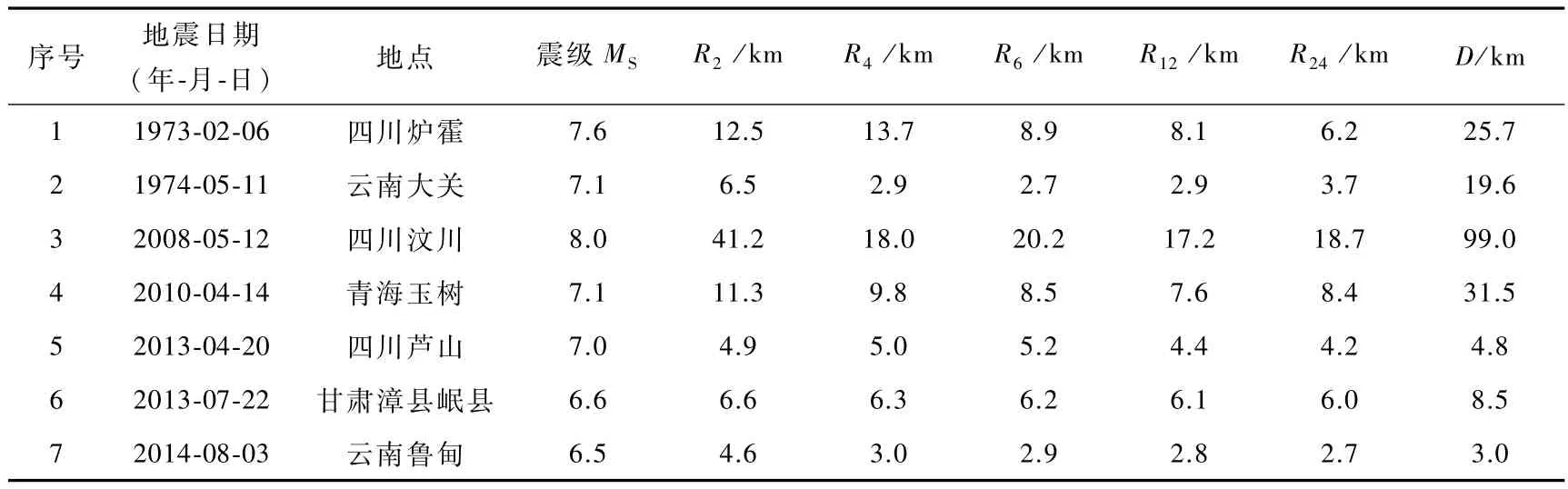
表4 估计震中、微观震中与宏观震中的距离

7次地震各时段估计震中、微观震中与宏观震中的距离均值如表5所示。

从表5可以看到，每个时段估计震中都有效缩小了微观震中与宏观震中的偏离，震后 2、4、6、12、24h的估计震中相对于微观震中的精度分别提升了54.37%、69.46%、71.54%、74.45%、74.01%。总体来说，震后 2h的估计震中偏差稍大，距离均值为12.52km，震后6h估计震中已经能够较好地反映宏观震中的位置，距离偏差为7.81km，最佳估计宏观震中出现在震后 12、24h，距离均值达到 7.0km左右。也就是说，随着时间的推移，估计震中越来越接近宏观震中，此时估计震中与实际宏观震中的差距能够达到7km左右。据此可认为，本文所述的方法明显改善了直接使用速报震中作为宏观震中而造成的偏移，尤其对于破坏性大地震而言，估计震中将有助于我们更加准确地估计极震区的大致位置，这对于震后灾害评估、应急救援应具有一定指导意义。

表5 各时段估计震中、微观震中与宏观震中的距离均值计算结果

3 讨论

余震能量场估计极震区和地震灾害调查评估结果的对比表明，估计的极震区与地震重灾区分布特征具有较好的一致性。然而主震破裂和余震分布之间并不总是严格的相互对应，震源破裂区一般伴随着余震分布，但余震分布区不一定有破裂发生。如玉树地震的破裂主要向东南方向传播（张勇等，2010），但在震中西北约40km处，也存在着比较密集的余震（王长在等，2013）。另外，大地震破裂过程的复杂性导致了震源区同震位移场的非均匀性，仅仅通过余震频度或能量场难以得到地表位移的细节，因此本文的估计极震区仅为较为粗糙的结果。

由于无法确定个别边缘（不包含主轴方向）的不连续地震是主震区激发余震还是边缘触发地震，因此在确定宏观震中时，剔除了个别边缘不连续地震（N≤3）或高能量小斑块。余震分布信息随着时间推移而不断增加，能量场空间分布也随之改变。研究显示，余震能量场震后2h估计震中可以作为宏观震中的修正因子，并在震后4h、6h、12h估计震中进行再次修正，最佳估计震中出现在12h。

能量场空间分布会受到余震定位精度和完整性震级的影响，但随着近些年来我国地震台网的加密、观测能力的不断增强，余震的定位精度和完整性震级的观测精度有很大的提高。此外，本文所选震例较少，上述结果还需要更多震例资料的补充验证。虽然精度仍有待提高，但利用震后12h内余震能量场空间变化的估计震中作为震后烈度快速判定的修正震中，显然在时效性上基本可以满足震后烈度快速判定的需求，显著缩小微观震中与宏观震中的差距，这对于应急救灾而言无疑能够提供更好的决策依据。