巧设问题情境

许玲丽

笔者在教学第十册“分数的基本性质”一课时，通过认真阅读分析教材，结合学生的思维能力和认知水平考虑，认为依照课本上编排的程序进行教学，会在一定程度上限制学生创造性思维的发展。于是，笔者大胆改进教学设计方案，直接创设问题情境，导入新知。首先出示问题：你会用分数表示下图中阴影部分的大小吗？

学生在已有“分数的意义”这一认知基础上，首先想到的答案是[48]，再通过深入观察思考，又有学生说出“[24]、[12]”，也可以表示图中阴影部分的大小。一些学生顿生疑问，产生认知冲突，内心处于一种不平衡状态，急切渴望再学习、再探究。

学生有了强烈的学习欲望，笔者又不失时机地为他们创造条件，让他们按四人一组合作研究、自主探索。

学生在各自的小组中展开了热烈的讨论。有的学生认为，图中正方形平均分成了8份，阴影部分占了这样的4份，所以只有[48]这个答案正确。这些学生的思维还只停留在已有知识的层面上。有的学生认为三个分数表示的结果都正确，虽然图中把正方形平均分成了8份，我们可以把图中的每两个小三角形看作一份，这样就可以看作把正方形平均分成了4份，阴影部分占这样的2份。也可以把图中每两个正方形看作一份，这样这个图形就可以被看作平均分成了2份，阴影部分占这样的l份，所以用[24]、[12]表示阴影部分也正确。这些学生的思维活动就更深入了一步，并且还动手画出下列图形进行展示：

学生们争论不休的时刻，也正是他们在积极参与整个学习活动，经历着数学知识的探索过程的时刻。在这一讨论过程中，学生们之间的能力差别和潜在的创造力都展现了出来。他们在相互启发下，对问题有了新的答案。有的学生发现，[816]、[1632]也可以表示图中阴影部分的大小，他们边说明边折纸展示（如下图）来验证自己答案的正确性。

通过热烈争论，学生不仅有了新发现，思维品质也得到不断升华。有的学生大胆猜想：答案有无数个。

猜想是一种创造性的直觉思维方式，是关于数学规律的联想和设想。教学中，创设这样的问题情境，鼓励学生大胆猜想，对学生创造性思维的发展无疑会起到一定的促进作用。

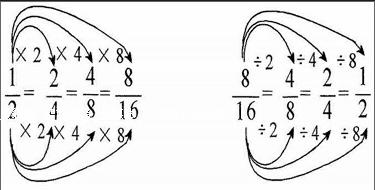
学生很快说出这一列分数大小相等，分子、分母都在不断变化，并正确地找出了分子、分母变化的规律。如下面板书：

在学生用简洁的语言概括出分数的分子、分母变化的规律后，紧接着，笔者把学生引入“验证”阶段，通过互动，用实例验证了分子、分母变化的规律，最后学生用具有代表性的例证[ab]=[a×cb×c]=[a÷cb÷c]（b、c都不为0）构建起“商不变性质”与“分数的基本性质”之间的内在联系，并概括出“分数的基本性质”这一重要结论。

通过这一课的教学，笔者深刻地认识到，在课堂教学中，应该完全以学生为主体，教师启发、引导都要适时，要巧妙创设问题情境，让学生去探索、总结，积极开展思维活动，这样我们才能真正把素质教育落实处。

（作者单位：荆门市教育科学研究所）