基于PSO-SVR的冷水机组运行能效预测模型研究

周璇　蔡盼盼　练斯甄　闫军威（华南理工大学机械与汽车工程学院　广州　510640）

基于PSO-SVR的冷水机组运行能效预测模型研究

周璇蔡盼盼练斯甄闫军威
（华南理工大学机械与汽车工程学院广州510640）

针对冷水机组运行能效模型结构复杂、受运行参数影响较大、机理建模困难等问题，本文建立了基于支持向量回归机的冷水机组运行能效预测模型，并采用粒子群优化算法对模型参数寻优，提高了模型的精度。论文以某商场中央空调离心式冷水机组为研究对象，随机选取396组运行数据对建立的模型进行训练和测试。结果表明，基于粒子群算法优化的冷水机组支持向量回归机模型较BP神经网络模型具有较高的预测精度，其相对误差基本上在3％以内。最后分别采集夏季和过渡季两日的运行数据验证模型的有效性，验证相对误差均在5％以内，因此，该模型能准确地反应冷水机组的运行能效，为冷水机组运行能效分析、故障诊断以及优化控制等提供参考依据。

冷水机组；运行能效；预测模型；支持向量回归机；粒子群算法

冷水机组运行能效直接影响空调系统能耗，准确的冷水机组运行能效预测模型是空调系统节能优化运行与故障诊断的重要基础［1］。冷水机组结构复杂，且其运行能效受冷冻水供水温度、机组负荷率、冷却水进水温度等多种因素的影响，运行能效预测建模过程复杂。诸多学者和研究人员对冷水机组建模进行了深入研究。Lee T S等［2］通过选择与建筑负荷相匹配的冷水机组及其结构参数，建立了变流量工况下的冷水机组模型。Jin G Y等［3］利用经验和半经验模型建立了冷水机组的混合模型，其中的模型参数通过实验数据拟合获取。传统的机理建模方法精度较高，但模型结构较复杂、模型参数较多且难以确定，工程应用较困难。由于黑箱模型相对简单有效，易用于工程应用。Manohar H J等［4］采用BP神经网络建立了吸收式冷水机组的能效预测模型，即通过冷冻水供回水温度、冷却水进出水温度、蒸气压力共5个运行参数预测机组运行能效。Chang Yungchung［5］利用BP神经网络建立了水冷式冷水机组的能耗模型，通过冷冻水供回水温度与冷却水进水温度预测机组的能耗。虽然BP神经网络具有强大的非线性映射能力，但其预测模型的网络隐含层节点不易确定、容易陷入局部极小值。

支持向量回归机（support vector regression，SVR）以结构风险最小化原理为基础，能够较好的解决小样本、非线性、高维等问题，近年来已被应用于电力系统短期负荷预测、地下水位预测等领域［6］，在冷水机运行能效预测领域的应用尚不多见。本文拟利用支持向量回归机强大的非线性映射特性，研究冷水机组建模方法，并采用粒子群优化算法（particle swarm optimization，PSO）对SVR参数进行寻优，进一步提高冷水机组运行能效预测模型的精度，最后将其应用于商场冷水机组的运行能效预测建模。

1　方法及原理

1.1SVR算法

支持向量机（support vector machies，SVM）是20世纪90年代中期Vapnik等提出的一种以结构风险最小化为原理、充分利用有限样本学习获取较高泛化能力的机器学习方法［7］。支持向量回归机是支持向量机在函数回归领域的应用，对于非线性问题，SVR的基本思想是把非线性的训练数据映射到一个更高维的特征空间（Hilbert空间）中，在这个高维的特征空间中构造线性回归函数，实现原低维空间中的非线性回归。SVR的原理可描述为［8-9］：

对于给定的训练样本集，｛（x1，y1），（x2，y2）…（xl，yl）｝，其中xi∈RN表示输入向量，yi∈R表示输出值，l表示样本数量，在高维Hilbert空间中构造的回归函数为：

式中：φ（x）为输入向量x到Hilbert空间的变换；ω为Hilbert中的权值向量，ω∈RN；b为截矩，b ∈R。

根据结构风险最小化原理，求解回归函数f（x）问题可转化为求解下式：

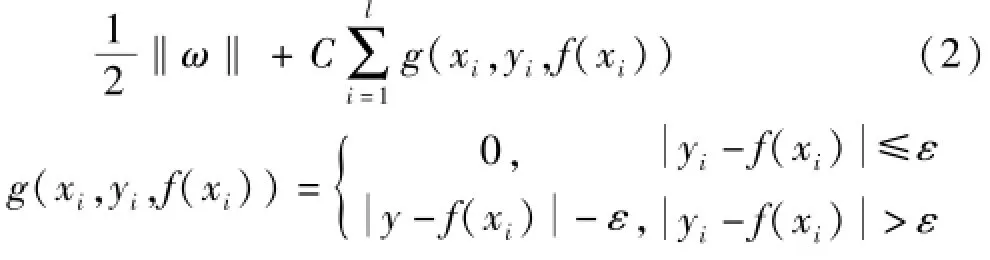
式中：ε为回归函数的拟合精度；常数C为超出精度ε的惩罚程度，C＞0。

同时考虑到允许拟合误差的情况，在式（2）中引入松弛因子ξi，ξi*，将优化目标转化为凸二次优化问题：对上述优化问题引入拉格朗日乘子αi和αi*，并通过满足Mercer条件的核函数Qij=φ（xi）Tφ（xj）=K（xi，xj）求解二次规划的对偶问题：

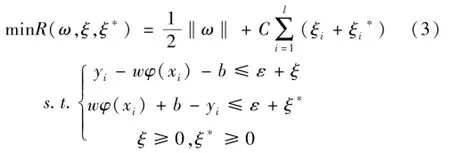
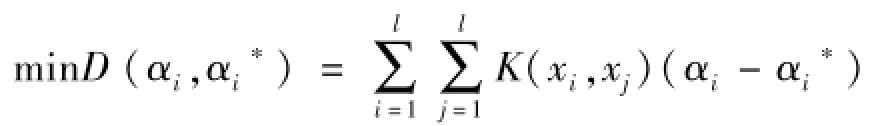
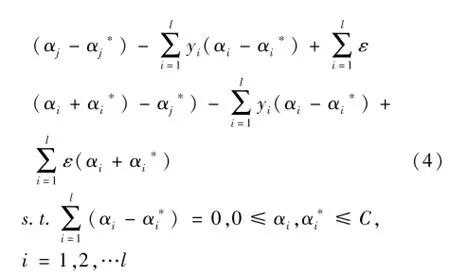
根据KKT定理，推导求出截矩b值，则回归函数f（x）可表述为：

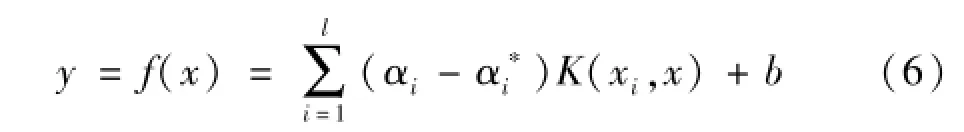
核函数K（xi，x）将样本集从输入空间非线性映射到高维特征空间，即通过非线性变换转化为另一空间中的线性问题。目前，常用的核函数主要有三种：线性核函数、多项式核函数和高斯径向基RBF核函数［10］。由于高斯径向基函数RBF核函数具有形式简单，较强的非线性逼近能力和良好的泛化性能［11］。本文选取高斯径向基函数为SVR核函数，如下式所示：

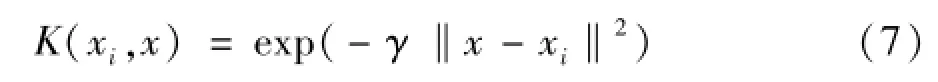
式中：γ表征高斯核函数的宽度。

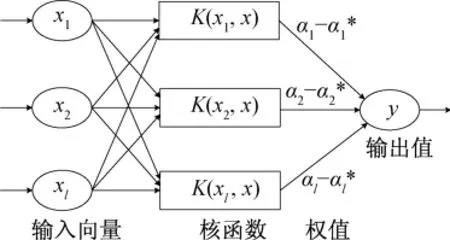
图1　SVR结构示意图Fig.1 Structure of SVR

1.2PSO算法

粒子群优化算法是一种采用速度-位置搜索模型、通过个体间的协作与竞争实现多维空间中最优解搜索的一种智能化优化算法［12］。在 D维搜索空间中，由m个粒子组成的种群记为 x=（x1，x2，…，xm）T，群体中第i个粒子在D维搜索空间内的位置记为xi=（xi1，xi2，…，xiD）T，其速度为vi=（vi1，vi2，…，viD）T，当前时刻的个体极值记为pibest，全局极值记为pgbest。在每一次迭代过程中，粒子通过跟踪t时刻个体极值、全局极值和自己的状态来更新t+1时刻的位置和速度，迭代公式如下［13-14］：

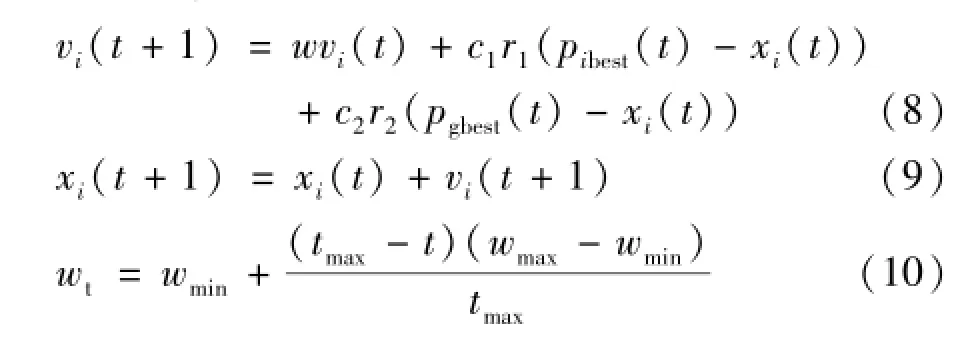
式中：vi（t），vi（t+1），xi（t），xi（t+1）分别为粒子t时刻、t+1时刻的速度和位置；pibest（t）为t时刻的个体极值；pgbest（t）为t时刻的全局极值；tmax为最大迭代次数；c1，c2称为学习因子，一般取值2；r1，r2为［0，1］上的随机数；w为惯性常数，wmax为最大权重因子，一般取值0.9，wmin为最小权重因子，一般取值0.4。

1.3基于PSO的SVR参数优化

SVR算法的分析可知，ε-SVR模型参数主要包括不敏感损失系数ε，惩罚系数C和高斯径向基RBF核函数的宽度系数γ，其中不敏感损失系数ε与样本噪声密切相关，决定回归函数对样本数据的不敏感区域宽度及支持向量的数目，直接影响模型的精度；惩罚系数C决定超出ε区间的惩罚程度，直接影响模型的稳定性和复杂性；宽度系数γ则反映支持向量的相关程度，直接影响模型的推广能力［15］。因此，（ε，C，γ）这三个参数的选择对SVR模型的性能有很大的影响。目前常用的参数选择法多采用经验法和试凑法，难以保证回归精度和计算速度，而PSO算法具有搜索速度快、效率高、算法简单、适合于实值型处理等优点，因此本文采用PSO算法对SVR的参数 （ε，C，γ）进行寻优。在PSO-SVR算法中，每个粒子由3维参数向量（ε，C，γ）组成，适应度函数选用直接反应SVR回归性能的均方根误差（RMSE）：

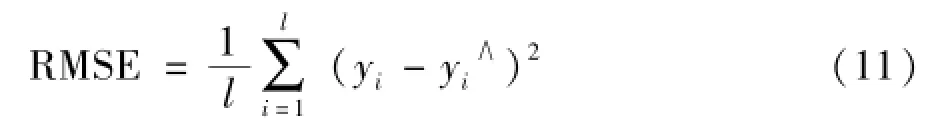
基于PSO的SVR模型参数寻优具体流程如图2所示。

2　冷水机组运行能效影响因素分析

2.1实验数据采集

本文以广州市某商场的离心式冷水机组为研究对象，探讨冷水机组运行能效建模方法。冷水机组型号为约克YKHFGBJ15CWF，额定制冷量为3517 kW，额定功率为647 kW。作者所在研究团队于2012年对该商场的中央空调系统进行了节能改造，增加了中央空调远程监控系统，可实现冷源系统各运行参数的实时采集、存储与统计分析，中央空调远程监控系统如图3所示。

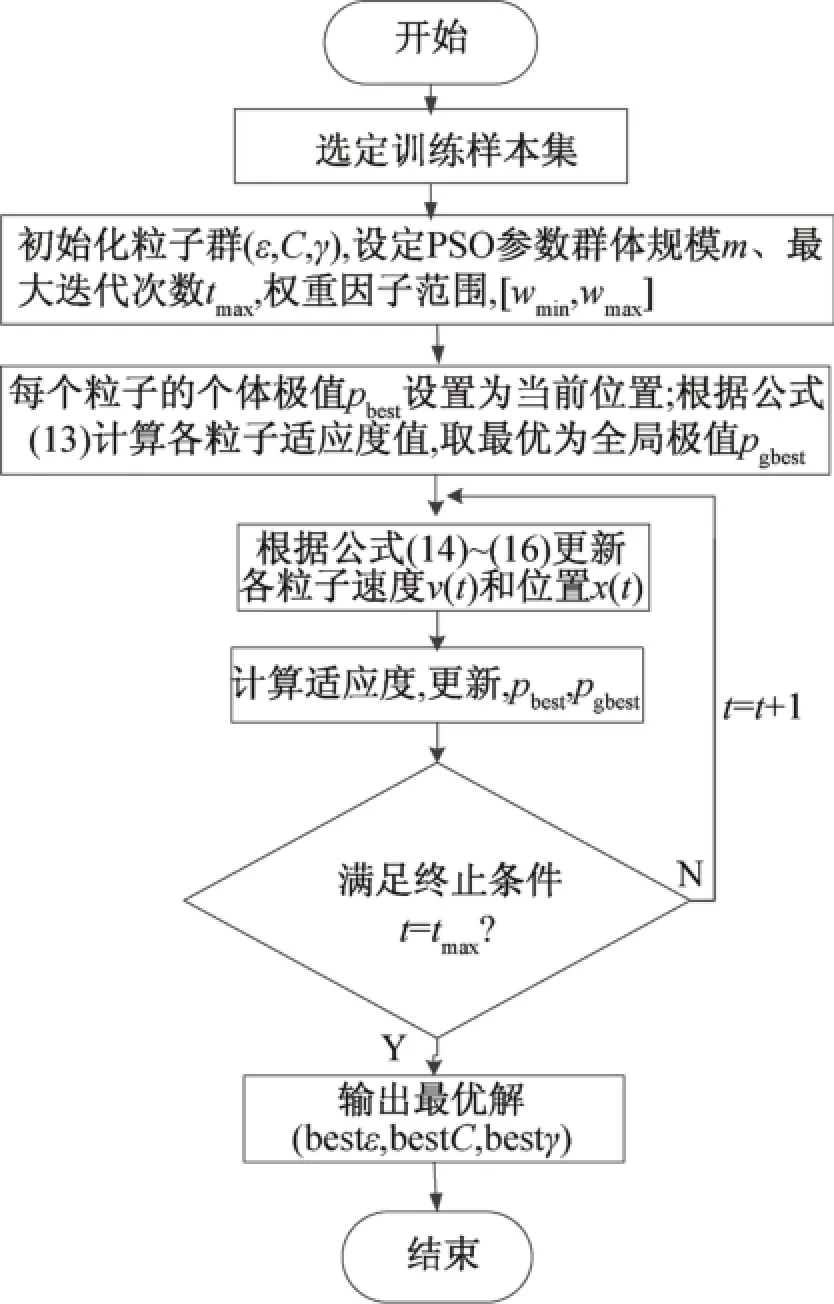
图2　PSO-SVR参数寻优流程图Fig.2 Flowchart of PSO-SVR parameter optimization

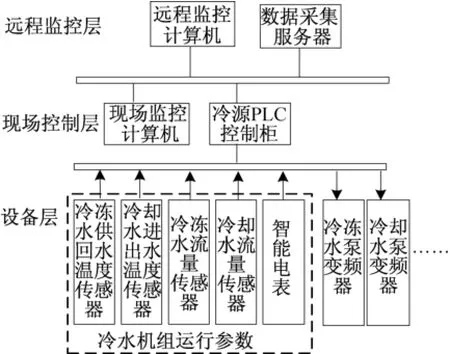
图3　中央空调远程监控系统框图Fig.3 The diagram of central air conditioning remote monitoring and control system

由图3可看出，水温传感器主要用于采集各冷水机组冷冻供回水温度、各冷水机组冷却进出水温度、冷冻水总管供回水温度和冷却水总管的进出水温度，超声波流量计用于采集各冷水机组冷冻水流量和冷却水流量，电功率表用于采集各冷水机组的运行功率。温度传感器、超声波流量计与电功率表测得的信号经过A/D转换后传给冷源PLC，冷源PLC采用将采集的数据上传至数据采集服务器，数据采集服务器利用TCP/IP协议，通过Internet/Intranet网络系统将采集数据上传至远程监控中心。远程监控软件根据采集回来的运行参数进行优化分析，实现对设备的集成优化控制。

冷水机组的供冷负荷率和机组的运行能效则通过式（12）～式（14）计算得到。

式中：Qc为供冷负荷，kW；cp为冷冻水比热，J/ （kg.℃）；Me为冷冻水质量流量，kg/s；Tei为冷冻回水温度，℃；Teo为冷冻供水温度，℃；PLR为供冷负荷率，％；Qr为冷水机组额定制冷量，kW；P为冷水机组电机输入功率，kW。

2.2影响因素分析

冷水机组运行能效受供冷负荷率、冷冻水供回水温度、冷却水供回水温度、冷冻水流量、冷却水流量等诸多因素影响，且各种影响因素之间也存在着错综复杂的交互关系，因此，冷水机组运行能效模型具有复杂性、非线性、高维数等特点。为了研究各运行参数对冷水机组运行能效的影响程度，本文利用SPSS软件对冷水机组运行能效与多个影响因素进行了相关性分析，通过常用的Pearson相关系数和双侧显著性检验（T统计量，显著性概率p＜0.01）得到的相关系数分析结果见表1。

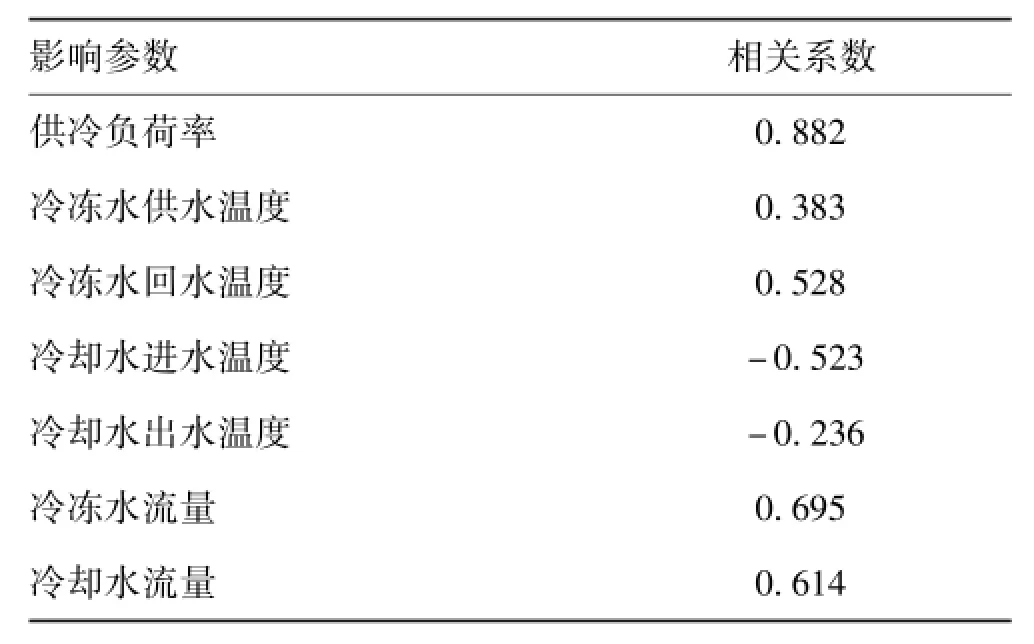
表1　机组COP与影响参数相关性分析Tab.1 Correlation analysis between chiller's COPand its influence parameters

由表1可以看出，冷水机组运行能效的影响因素相关系数大小依次为：供冷负荷率、冷冻水流量、冷却水流量、冷冻水回水温度、冷却水进水温度、冷冻水供水温度和冷却水出水温度，而实际上供冷负荷率已间接反映了冷冻水回水温度，因此本文选取相关系数较大的供冷负荷率PLR、冷冻水供水温度Teo、冷却水进水温度Tci、冷冻水流量Me、冷却水流量Mc共5个主要因素作为模型的输入参数，冷水机组的运行能效比COP作为模型的输出参数。

3　仿真实验

3.1数据处理

由于SVR模型的输入输出数据具有不同的物理意义，为了消除量纲的影响，需要将影响冷水机组运行能效模型的输入变量和输出变量进行归一化处理，本文采用最大最小值的方法将样本数据处理成［0，1］的无因次数，有效提高回归计算效率，并防止部分不良数据计算溢出的现象，计算方法如下：

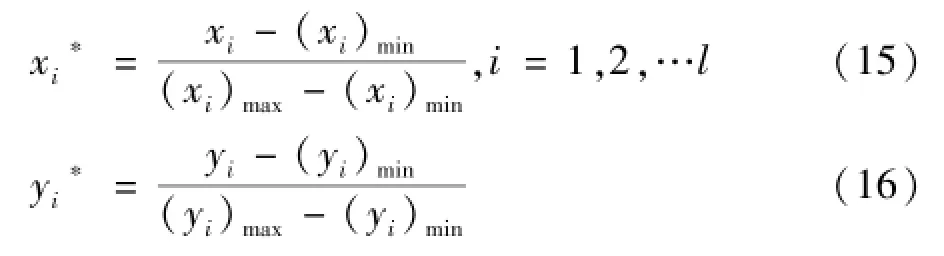
式中：xi为输入变量；yi为输出变量；x*i为归一化后的输入变量；yi*为归一化后的输出值；l为输入参数个数。

3.2模型建立

基于PSO-SVR冷水机组运行能效模型方法的主要思想就是将影响因素（Teo，Tci，Me，Mc，PLR）iT作为SVR模型的输入向量，将相应的冷水机组运行能效COPi作为SVR模型的输出值，通过PSO算法对SVR参数（ε，C，γ）的寻优、训练样本的学习，确定回归函数的回归参数，从而建立PSO-SVR冷水机组运行能效模型。基于PSO-SVR冷水机组运行能效模型建立流程如图4。

3.3实验结果分析

本文从2013年8月16日～2014年8月16日全年的运行数据库中随机选取396组运行数据进行建模，每组数据均包括冷冻水流量、冷却水流量、冷冻水供水温度、冷却水进水温度和冷水机组运行能效等参数，部分运行数据见表2。选用前300组运行数据作为训练集，建立PSO-SVR冷水机组运行能效模型，选用剩余的96组运行数据作为测试集，检验PSO-SVR冷水机组运行能效模型。

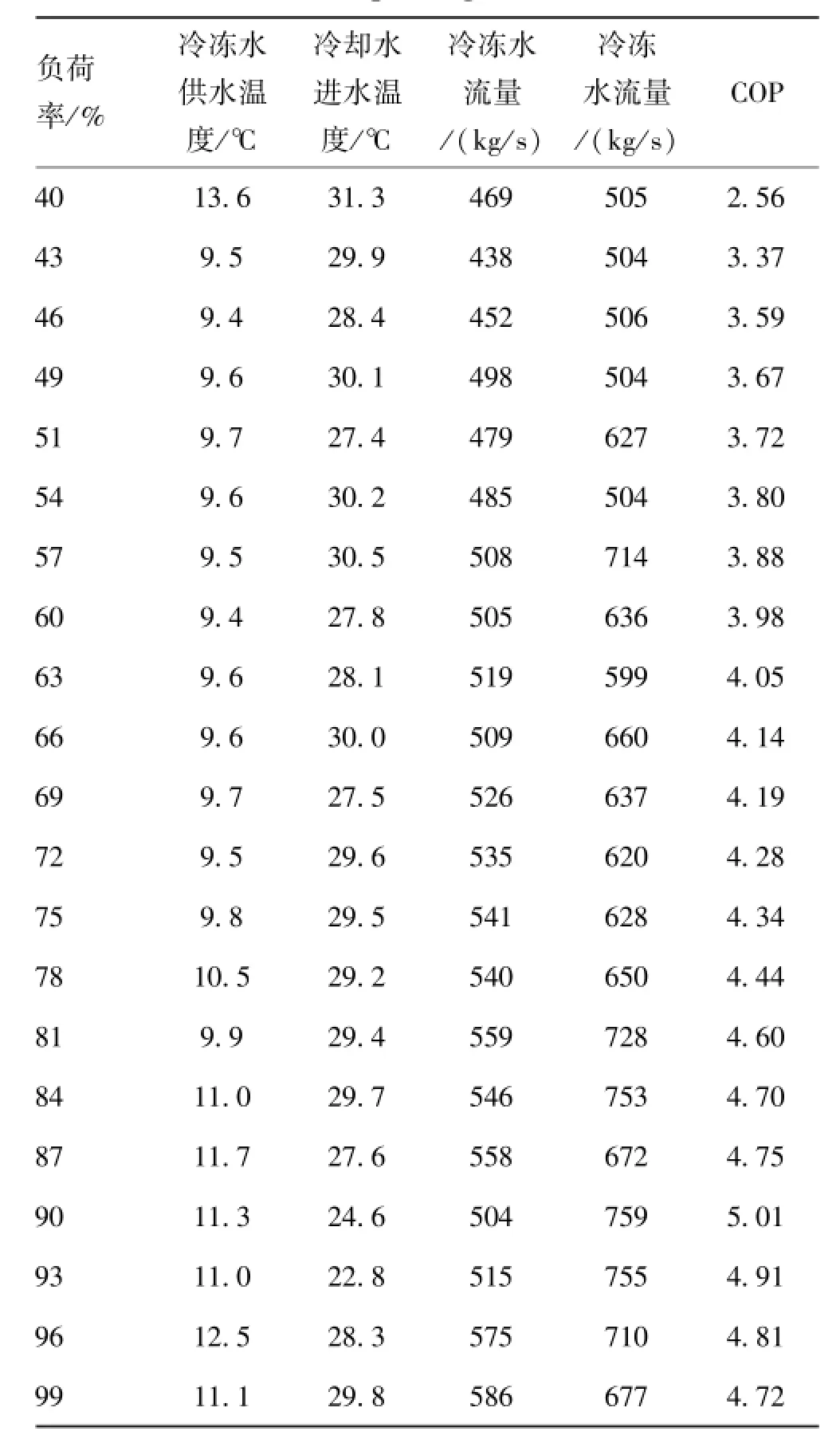
表2　冷水机组部分运行数据Tab.2 Some operating data of chiller

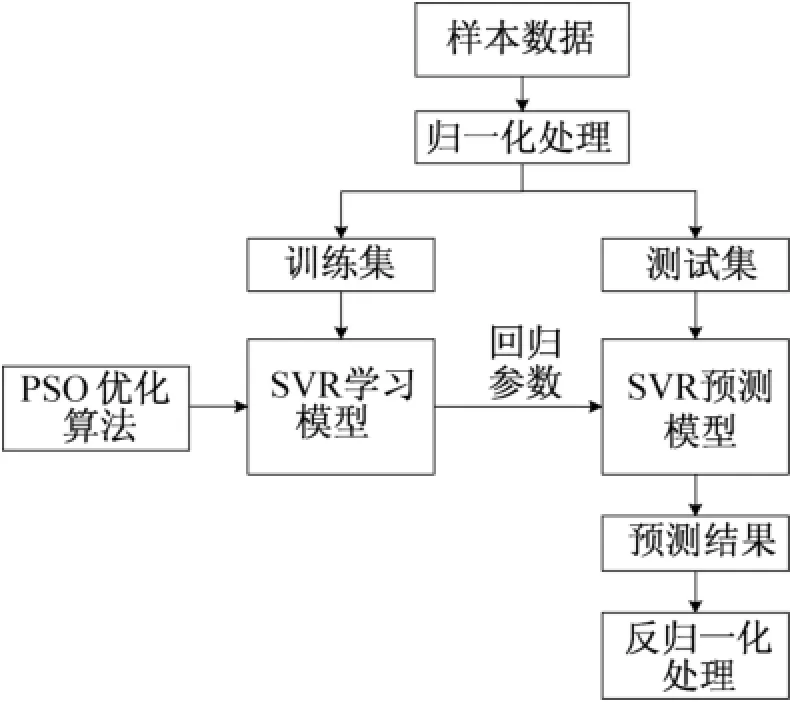
图4　基于PSO-SVR冷水机组运行能效模型流程图Fig.4 Flowchart of COP model based on PSO-SVR

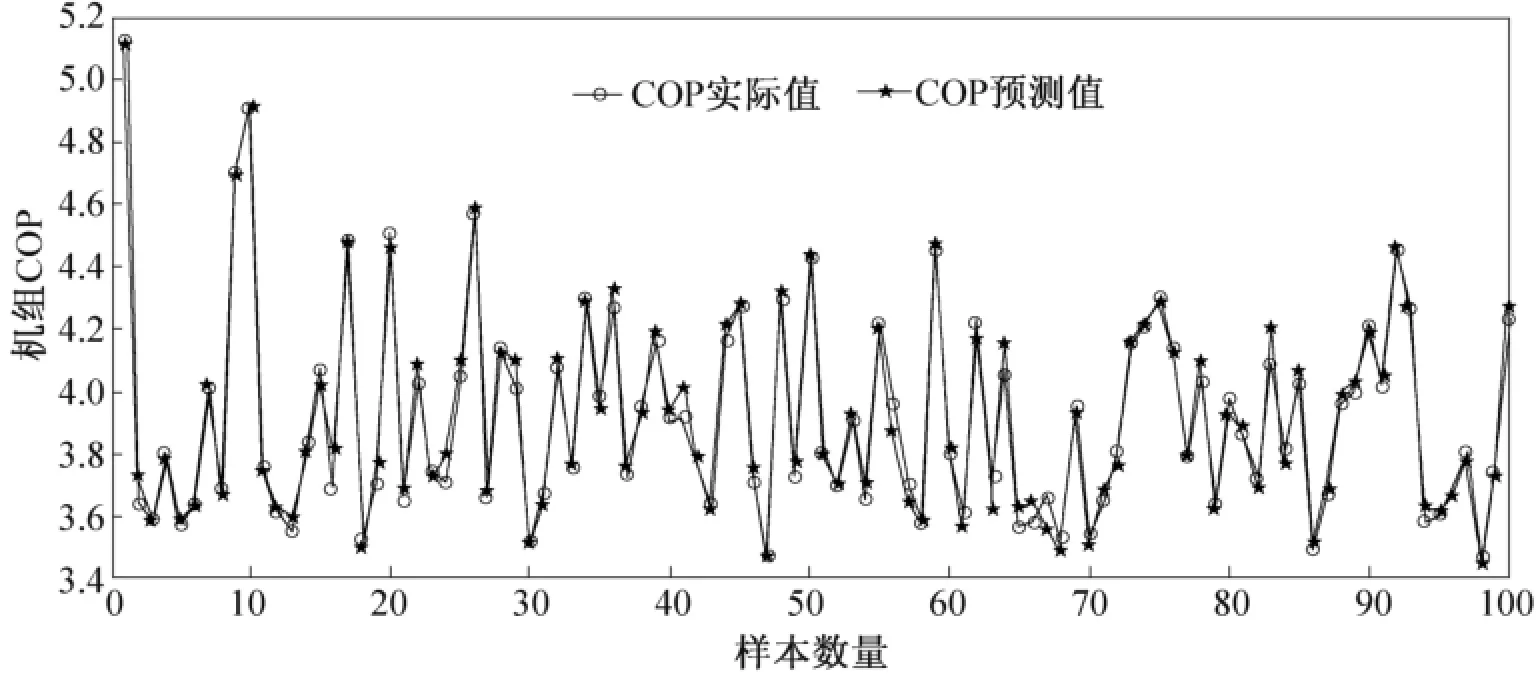
图5　PSO-SVR模型对部分训练集的预测效果Fig.5 Prediction of training set by PSO-SVR model

利用PSO算法优化SVR参数时，（ε，C，γ）参数的取值范围分别设置为［16］：ε的取值范围为［0，0.5］；C的取值范围为［1，103］；γ的取值范围为［0，102］，粒子群规模设为50，最大进化代数设为100代，得到优化结果为ε=0.0013，C=6.28，γ =2.60，相应的均方根误差 RMSE为 0.00195。PSO-SVR模型对训练集的预测效果如图5。从图中可看出，PSO-SVR模型的预测值与真实值非常接近，PSO-SVR模型获得了准确的输入输出行为，可有效地表达冷水机组运行能效和相关运行参数的关系。

利用建模剩余的96组运行数据作为测试集，对建立的冷水机组运行能效PSO-SVR模型进行检验，同时与BP神经网络模型方法进行了对比分析，预测结果与误差曲线如图6和图7所示。

从图6、图7可以看出，PSO-SVR模型的预测相对误差普遍低于BP神经网络模型的预测相对误差，基本在3％以内，而BP神经网络模型预测效果相对较差，一般在5％左右。这是因为在小样本情况下，常规SVR模型和BP神经网络模型易出现训练不足或过学习的情况，难以保证模型的精度，而PSO-SVR模型在训练过程中，通过PSO算法优化模型参数，有效避免了过学习现象，增加了模型的泛化能力。

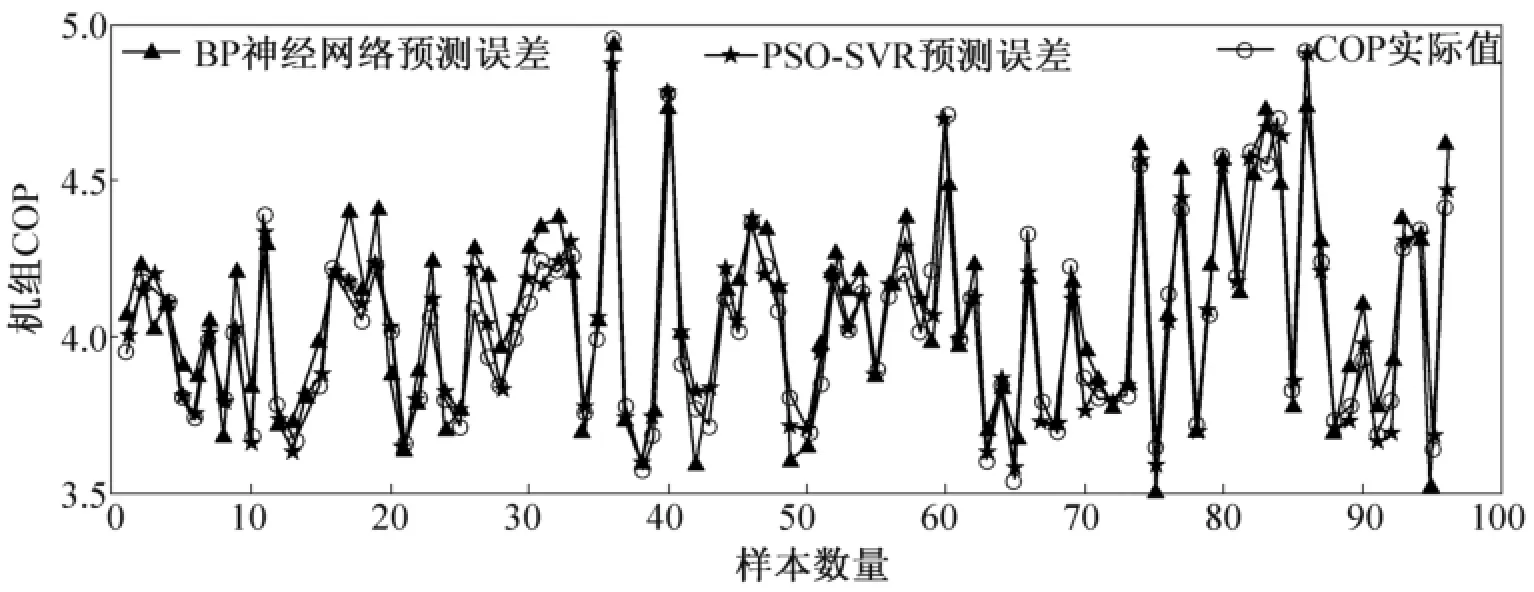
图6　BP神经网络与PSO-SVR冷水机组运行能效预测结果比较图Fig.6 Comparison of BP model and PSO-SVR model of COP

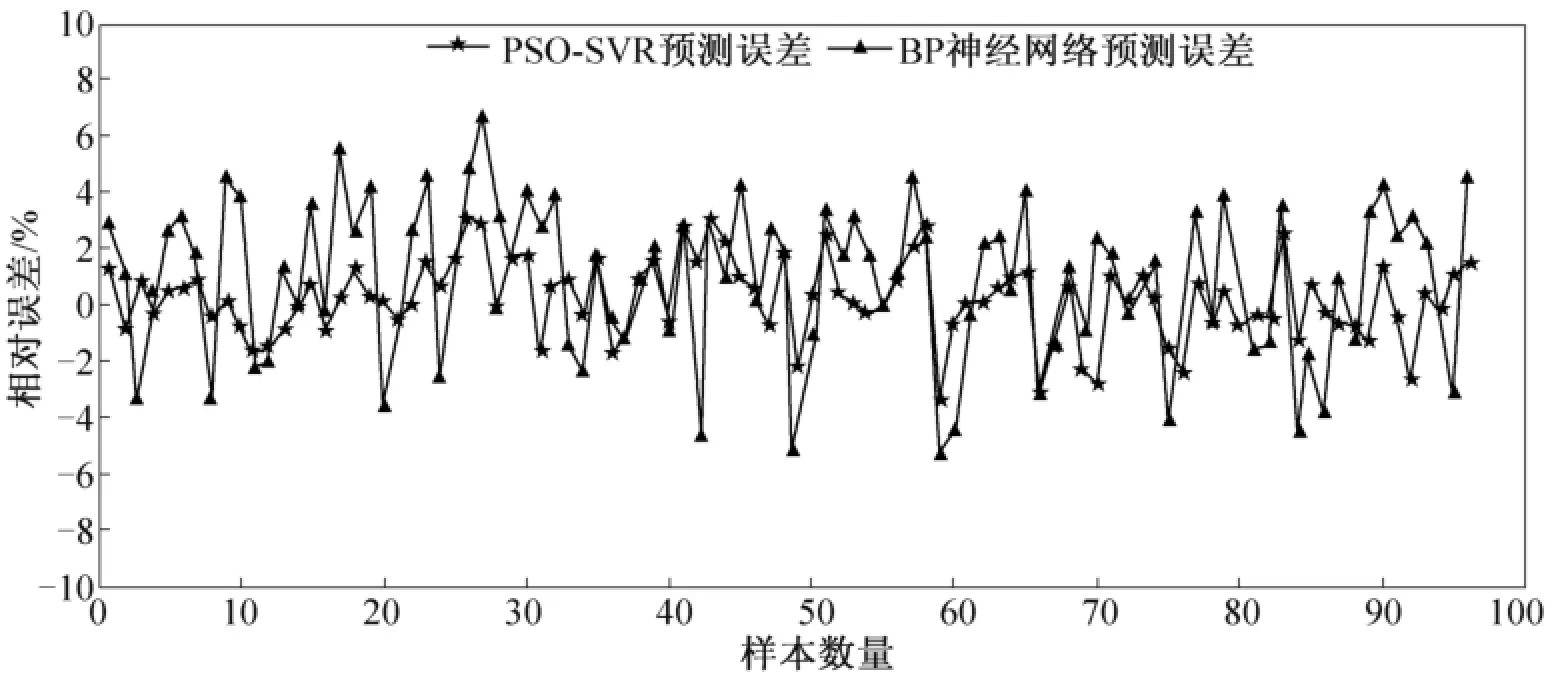
图7　BP神经网络与PSO-SVR冷水机组运行能效预测相对误差比较图Fig.7 Relative error comparison of BP model and PSO-SVR model of COP

3.4实验测试

为验证PSO-SVR冷水机组运行能效模型的适用性，本文任意选取夏季和过渡季各一天的运行数据对上述PSO-SVR冷水机组运行能效模型进行测试，选取的运行数据为20组，间隔时间为30 min。预测结果如表3所示。

由表3可知，将建立的PSO-SVR冷水机组运行能效模型用于预测不同季节日的冷水机组运行能效时，同样具有较高的预测精度，两天的预测最大相对误差均在5％以内，最小相对误差均低于1％，平均相对误差分别为2.36％和2.04％，均在3％以内。由此可见，建立的PSO-SVR冷水机组运行能效模型应用于实际工程中能够较好反映冷水机组的实时能效。

4　结论

本文提出了冷水机组运行能效模型的PSOSVR建模方法，采用PSO算法对SVR模型参数进行优化，增加了模型的泛化能力，提高了模型的精度，并以广州某大型商场离心式冷水机组为例，从全年数据库中随机选取396组运行数据进行模型的训练和测试。仿真结果表明，与BP神经网络模型相比，PSO-SVR模型精度较高，预测相对误差均在3％以内。最后为了进一步验证PSO-SVR模型的推广性，分别采集夏季和过渡季两日的运行数据进行测试，每日采集20组运行数据，采集周期为30 min，测试相对误差均在5％以内，平均相对误差均在3％以内。因此，PSO-SVR冷水机组运行能效模型能够较好反映冷水机组的实时能效，且建模方法简单，具有工程应用价值，可为冷水机组运行能效分析、节能优化控制以及故障诊断等提供参考依据。

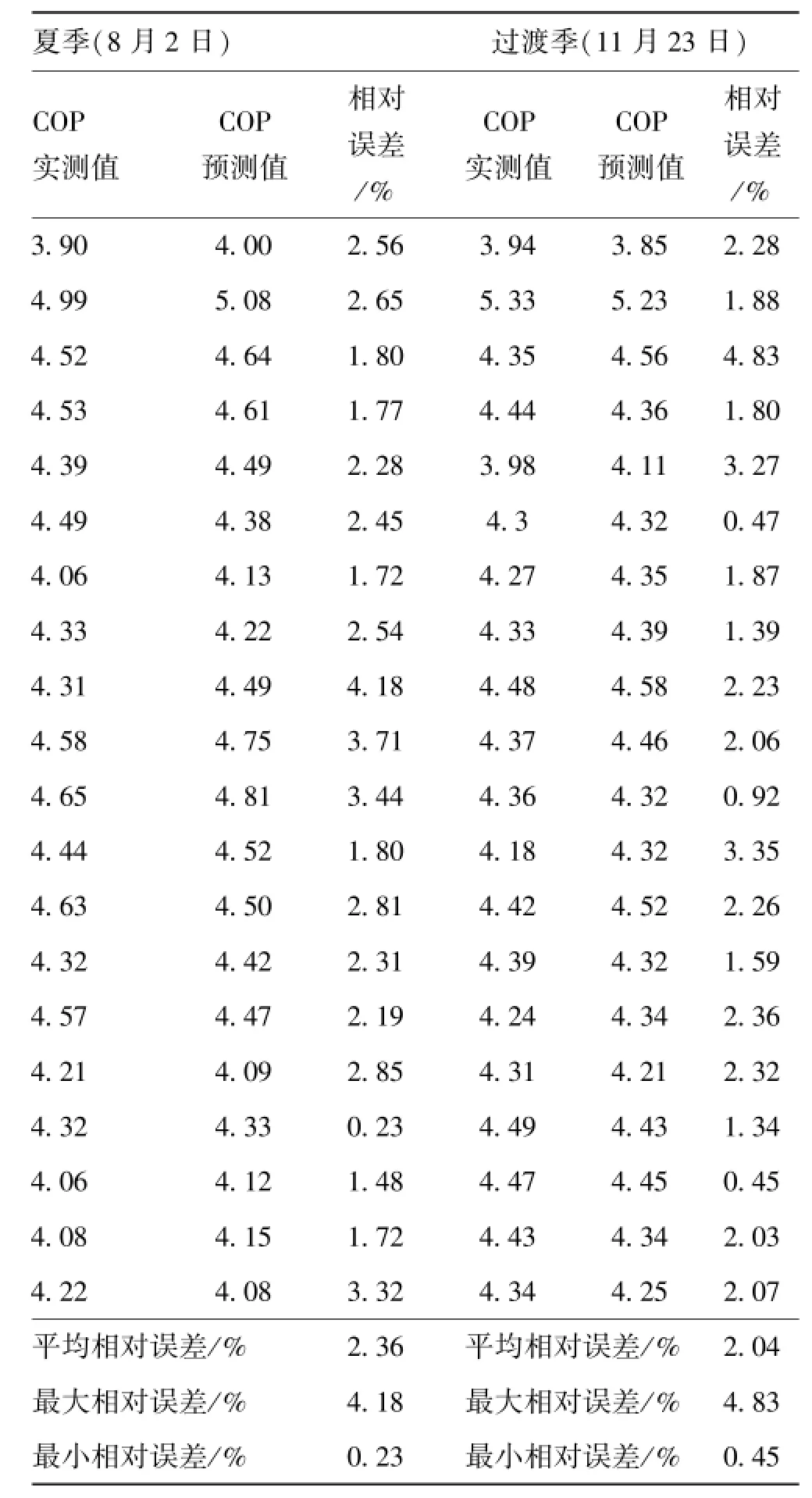
表3　PSO-SVR冷水机组运行能效模型测试相对误差Tab.3 Tested relative error of PSO-SVR model

本文受广东省科技厅支撑项目——中央空调运行能效在线检测与优化控制（2011B061200043）资助。（The project was supported by the Guangdong Provincial Department of Science and Technology Project：Online Inspection and Optimal Control of Central Air-conditioning Operation Energy Efficiency （No.2011B061200043）.）

［1］严中俊，闫军威.基于BP神经网络的冷水机组能效预测方法［J］.制冷与空调（四川），2013，27（5）：443-446.（Yan Zhongjun，Yan Junwei.The COP prediction method of chillers based on the BP neural network［J］.Refrigeration and Air Conditioning，2013，27（5）：443-446.）

［2］Lee T S，Liao K Y，Lu W C.Evaluation of the suitability of empirically-based models for predicting energy performance of centrifugal water chillers with variable chilled water flow［J］.Applied Energy，2012，93（Suppl.）：1721-1729.

［3］Jin G Y，Tan P Y，Ding X D，et al.A hybrid watercooled centrifugal chiller model［C］//In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications，2011：2298-2303.

［4］Manohar H J，Saravanan R，Renganarayanan S.Modeling of steam fired double effect vapor absorption chiller using neural network［J］.Energy Conservation and Management，2006，47（15/16）：2202-2210.

［5］Chang Yungchung.Sequencing of chillers by estimating chiller power consumption using articial neural networks ［J］.Building and Environment，2007，42（1）：180-188.

［6］梁伟锋.支持向量回归机研究及应用［D］.杭州：浙江师范大学，2006.

［7］辛宪会.支持向量机理论、算法与实现［D］.郑州：解放军信息工程大学，2005.

［8］杨际祥，谭国真，王凡，等.实时交通流预测的并行SVR预测方法［J］.大连理工大学学报，2010，50（6）：1035-1041.（Yang Jixiang，Tan Guozhen，Wang Fan，et al.A parallel SVR approach to real-time traffic flow forecasting［J］.Journal of Dalian University of Technology，2010，50（6）：1035-1041.）

［9］阎满富，田英杰.改进的支持向量回归机［J］.系统工程，2004，22（10）：9-13.（Yan Manfu，Tian Yingjie.Improved SVR［J］.Systems Engineering，2004，22（10）：9-13.）

［10］李红英.支持向量分类机的核函数研究［D］.重庆：重庆大学，2009.

［11］王治.基于混沌粒子群优化SVR的网络流量预测［J］.计算机仿真，2011，28（5）：151-154.（Wang Zhi.Network traffic prediction based on SVR optimized by chaos particle swarm optimization algorithm［J］.The Computer Simulation，2011，28（5）：151-154.）

［12］黄继，薄玉成，王惠源.基于混沌粒子群SVR的烟气轮机状态预测［J］.计算机仿真，2011，28（5）：193-196.（Huang Ji，Bo Yucheng，Wang Huiyuan.Flue gas turbine state forecasting by chaos particle swarm optimization and SVR［J］.The Computer Simulation，2011，28（5）：193-196.）

［13］傅强，胡上序，赵胜颖.基于PSO算法的神经网络集成构造方法［J］.浙江大学学报（工学版），2004，38（12）：1596-1600.（Fu Qiang，Hu Shangxu，Zhao Shengying. PSO-based approach for neural network ensembles［J］. Journal of Zhejiang University（Engineering Science），2004，38（12）：1596-1600.）

［14］唐俊.PSO算法原理及应用［J］.计算机技术与发展，2010，20（2）：213-216.（Tang Jun.Principle and application of PSO algorithm［J］.Computer Technology and Development，2010，20（2）：213-216.）

［15］熊伟丽，徐保国.基于PSO的SVR参数优化选择方法研究［J］.系统仿真学报，2006，18（9）：2442-2445.（Xiong Weili，Xu Baoguo.Study on optimization of SVR parameters selection based on PSO［J］.Journal of System Simulation，2006，18（9）：2442-2445.）

［16］练斯甄，周璇，闫军威.基于改进BP神经网络的冷水机组IPLV预测方法［J］.建筑科学，2014，30（6）：68-72.（Lian Sizhen，Zhou Xuan，Yan Junwei.Prediction techinque of integrated part load value（IPLV）of water chillers based on improved BP neural network［J］.Building Science，2014，30（6）：68-72.）

About the corresponding author

Zhou Xuan，female，associate professor，supervisor of postgraduate，School of Mechanical&Automotive Engineering，South China University of Technology，+86 13631378083，E-mail：zhouxuan @scut.edu.cn.Research fields：energy energy-saving control of air-conditioning system，load forecasting of central air-conditioning system.

Research on COP Prediction Model of Chiller Based on PSO-SVR

Zhou Xuan Cai Panpan Lian Sizhen Yan Junwei
（School of Mechanical&Automotive Engineering，South China University of Technology，Guangzhou，510640，China）

Since the difficulty of building mechanism model and the structure of COP model of chiller is complex，greatly affected by operating parameter，a COP prediction model of chiller is proposed based on Support Vector Regression，and the parameters are optimized by Particle Swarm Optimization algorithm.In this paper，396 sets of operating data of chiller of a shopping mall are randomly selected to train and test this model.The results shows that the prediction accuracy of SVR model based on PSO optimization algorithm is higher than that of BP neural network and the relative error is within 3％.At last，operating data of two days in summer and transition season are randomly selected to verify the model.The relative error is within 5％.So this model can provide theoretical basis for the chiller energy efficiency analysis，fault detection and diagnosis and optimizing control.

chiller；COP；prediction model；support vector regression；particle swarm optimization

TB657.2；TU831；TP391.9

A

0253-4339（2015）05-0087-08

10.3969/j.issn.0253-4339.2015.05.087

2015年2月5日

简介

周璇，女，副研究员，硕士生导师，华南理工大学机械与汽车工程学院，13631378083，E-mail：zhouxuan@scut.edu.cn。研究方向：空调负荷预测、空调系统节能优化控制。