两柱掩护式液压支架姿态监测技术研究

文治国，侯 刚，王彪谋，任怀伟，赵国瑞

(天地科技股份有限公司开采设计事业部，北京100013)

由于液压支架应用在煤矿井下，工作环境恶劣，为适应工作面采场围岩及煤层的变化，支架姿态经常发生变化，如果姿态异常将会导致支架整体失稳甚至造成关键零部件损坏。尤其在工作面推进距离达到周期来压步距或产生冲击地压等灾害事故时，顶板下沉量及下沉速度会成倍增加，支架姿态的合理变化就显得尤为重要［1－3］。因此，本文基于工作面实际工况，以ZY6800/11.5/24D型两柱掩护式支架为例，对两柱掩护式液压支架姿态监测方法进行研究。

1 液压支架姿态监测方法的提出

为了实现对液压支架姿态的实时监测，需要在支架相关部件上安装传感器。考虑到安装的方便及易维护性，以三倾角传感器作为数据来源进行分析计算。其中在顶梁和底座各布置1台倾角传感器，而另外1台传感器虽经理论分析布置在掩护梁、前连杆、后连杆均可，但考虑到倾角传感器测量角度大于60°后精度会显著下降，而ZY6800/11.5/24D型支架前连杆角度在15～48°之间变化，因此将第3台倾角传感器布置在前连杆上，并由此确立了以顶梁、底座、前连杆角度为自变量的支架姿态监测方法。在此基础上，通过创建模型，对姿态算法进行推导。

1.1 姿态数学模型建立

建立如图1所示的支架二维杆系模型，不考虑销轴间隙影响。

图1 支架二维杆系模型

图1中，L1～L5分别为顶梁、掩护梁、前连杆、后连杆及底座的长度;L6～L9是立柱的定位尺寸;L10～L13是平衡千斤顶的定位尺寸;H为支架的支撑高度;X，Y分别为立柱和平衡千斤顶工作时的长度;α，β，γ分别为顶梁、前连杆、底座与水平面夹角 (由3个倾角传感器实时测得)，其他参量如图1所示。

1.2 姿态数学表达式求解

为提出支架姿态数学表达式，根据图1所示支架杆系模型，建立以O为原点，竖直向上为+Y，水平向左为+X的平面坐标系，A～K代表支架不同结构件间的连接铰点，XA～XK，YA～YK为不同铰点在该坐标系下的坐标值，以α，β，γ为自变量可直接建立的铰点坐标计算公式为:

利用上述铰点坐标公式建立支架姿态的参数式方程并进行求解，可得出支架在纵向平面内任意时刻的姿态参数，根据两点间的距离公式，支架支撑高度H、立柱工作长度X、平衡千斤顶工作长度Y可分别表示如下:

2 液压支架虚拟样机的建立

选用 SolidWorks软件建立 ZY6800/11.5/24D型两柱掩护式液压支架虚拟样机，并对整架进行运动学仿真。

液压支架结构复杂，因此建模时在不影响支架运动学仿真的前提下忽略次要因素，简化模型结构，提高建模速度。其基本建模假设原则如下:

(1)不改变液压支架部件轴心的距离和位置。

(2)不改变主要部件和零件的尺寸。

(3)简化次要零件受力小的部分，如竖筋板、横筋板与顶 (或底)盖板交结部以外的顶 (或底)盖板部分。

(4)忽略样机的次要零件对整架主要结构件的受力状况产生的影响［2－5］。

基于上述原则，按照所选ZY6800/11.5/24D型两柱掩护式液压支架零部件二维尺寸图，在SolidWorks环境中建立支架零部件三维几何模型并进行装配。操作中按照各部件间相互运动关系，使配合定位准确，并利用SolidWorks的干涉检查评估体系对支架结构进行静态干涉检查［3］，经过多次修改和优化，得到如图2所示虚拟样机模型。

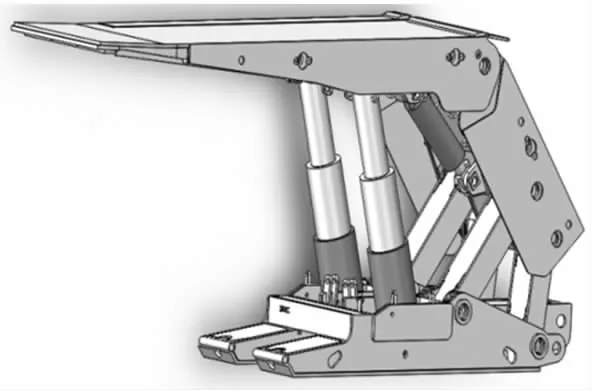
图2 虚拟样机模型

3 液压支架运动学仿真

采用SolidWorks软件的Motion插件，对已建立好的虚拟样机进行运动学仿真。为便于分析，首先做如下假定:

(1)不考虑各连接处的间隙。

(2)销轴端面与所连接的构件表面平行且距离值恒定，即约束了销轴在X和Y平面的自由转动及Z平面的移动。

(3)立柱和千斤顶的活塞杆与其所配合的油缸同轴心，即不考虑偏斜情况的存在。

(4)机构的主动力源作用于立柱，将活柱和内缸体作为运动件来考虑，二者沿轴线方向运动，其行程即为运行位移［4－8］。

基于上述假定，在SolidWorks/Motion环境中，设定各仿真参数，仿真结果以excel文件存储，对不同数据量化处理，进行二次分析，结果如下:

(1)当平衡千斤顶伸长量为零，底座水平时，立柱伸长量由零升至最大过程中，顶梁在不同高度允许最大俯角值如图3所示。

分析图3曲线可知，支架立柱伸长量为最大时，顶梁允许最大俯角值约为5°，当大于5°时支架平衡千斤顶将发生干涉，行程为负值，并可能造成连接件 (如销孔、销轴)的断裂或平衡千斤顶结构件的永久损坏。因此，在检测到支架顶梁俯角接近5°时，需对平衡千斤顶活塞腔及时补压，即进行推平衡千斤顶操作，并同时适当降柱，调整姿态，避免支架损坏。而在使用过程中，支架实际支撑高度小于最大支撑高度，因此选取图中相应高度所对应的最大俯角值 (此时大于5°)作为支架姿态监测调整的新判据，并以图5所示相同立柱伸长量时对应支架高度为理想调整状态对支架进行合理调控。

图3 顶梁最大俯角

(2)当平衡千斤顶伸长量为全部行程，底座水平时，立柱伸长量由零升至最大过程中，顶梁在不同高度允许最大仰角值如图4所示。

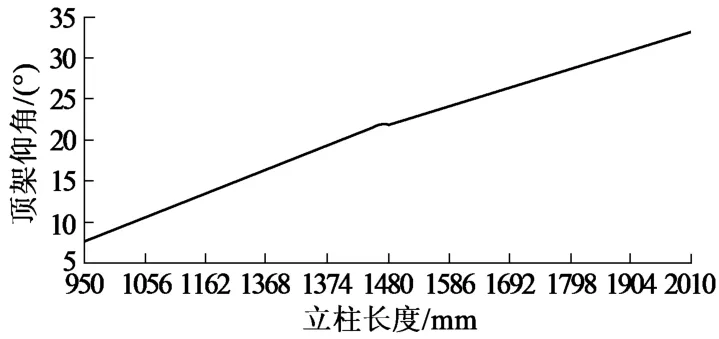
图4 顶梁最大仰角

由图4可知，支架立柱伸长量为零时，顶梁允许最大仰角值约为8°，当大于8°时，支架平衡千斤顶行程全部用完，并产生干涉，造成平衡千斤顶或支架的永久性损坏。当检测到支架顶梁仰角接近8°时，需对平衡千斤顶活塞杆腔及时补压，即进行拉平衡千斤顶操作，调整姿态，避免支架损坏。在使用中，根据支架实际支撑高度，选取图中相应高度对应的最大仰角值 (此时大于5°)作为支架姿态监测调整的新判据，并以图5曲线为目标对支架进行调控。

图5 支架高度与立柱长度关系曲线

4 姿态算法校验

假设支架顶梁与底座水平，并匀速上升，利用SolidWorks/Motion仿真插件绘制支架高度随立柱长度变化的关系曲线，如图5系列1所示。同时，利用VS2008将支架姿态算法编写为C++程序，通过编译运行，得到β由16°到48°并以2°递增时，支架高度与立柱长度变化量的17组对应数据，并拟合为曲线，如图5系列2所示。

由图5可知，姿态算法拟合曲线与虚拟样机模拟曲线走势基本相同，但有最大约为70mm的相对误差，经分析误差由三方面造成:一是程序运算中数据保留位不同;二是虚拟样机的构建存在一定误差;三是算法中对高次方程的求解不够准确。但从总体趋势来看，姿态算法基本正确，可作为支架姿态监测的理论基础。

5 结论

给出了两柱掩护式液压支架二维杆系模型，推导出了该型支架的姿态算法，并采用SolidWorks软件对支架进行了运动仿真，验证了支架姿态算法的正确性，结果表明，该算法可以用于液压支架姿态监测。

［1］白雪峰.掩护式支架姿态监测与控制的研究［D］.太原:太原理工大学，2006.

［2］朱殿瑞.掩护式液压支架姿态监测的理论与主要部件的有限元分析［D］.太原:太原理工大学，2012.

［3］杨培举.两柱掩护式放顶煤支架与围岩关系及适应性研究［D］.徐州:中国矿业大学，2009.

［4］王国法，徐亚军，孙守山.液压支架三维建模及其运动仿真［J］.煤炭科学技术，2003，31(1):42－45.

［5］任锡义.液压支架整体动态特性仿真分析［D］.太原:太原理工大学，2010.

［6］徐亚军，崔 柳，朱 军.基于虚拟样机的液压支架运动仿真和动态干涉检查 ［J］.煤矿机械，2004(12):67－69.

［7］彭 霖.液压支架静力学与运动学分析以及优化设计［D］.武汉:华中科技大学，2009.

［8］徐亚军，王国法，柴宾元，等.液压支架虚拟样机构建技术的研究［J］.煤矿开采，2003，8(4):8－10.