基于模糊熵权法的国际工程政治风险评价研究

缪朦朦，章恒全

(河海大学商学院，江苏 南京 211100)

0 引言

随着我国经济地位的上升以及经济版图的扩张，国内工程承包商不断拓展业务范围，从1979年开始进入国际市场并快速增长[1]，目前我国承包的国际项目遍布全世界180多个国家，涉及基础设施建设各个领域[2]。过去几十年来，诸如金融危机、恐怖主义、战争等政治和社会事件遍布全球各地，这些事件的发生加大了国际工程承包市场的不确定性，并在很大程度上影响了国际工程项目的顺利实施，使得国际工程项目承包商日益面临巨大的政治风险。因此，在国际工程项目实施过程中，承包商所面临的政治风险不容忽视。为顺应全球经济局势发展需求，我国国际工程承包商必须从自身出发，增强政治风险管理意识，提升风险识别和评估能力，强化风险管理，保证工程的顺利完成，增加项目的盈利能力与企业效益。

目前，国内外有关学者对政治风险的主要研究集中于以下两个方面:(1)政治风险影响因素识别和评估。(2)政治风险应对建议。美国国家风险国际指南(ICRG)采用评分法对世界各国进行国家风险等级定性评估，对预先设定的政治风险影响因素进行相应赋分并进行风险大小排序[3]。蔡强统计分析了项目风险管理人员的风险评价信息，以灰色相关系数作为指标参考权重，展开目标国政治风险的二元语义评价[4]。Deng等学者采用问卷调查等方法首先梳理了五大类政治风险影响因素，并运用统计分析法最终得出9项影响显著的风险因素[5]。从相关研究成果来看，目前学者针对政治风险的研究主要以外国投资者或跨国经营企业为视角，而专门针对国际工程项目政治风险管理的研究其分析和评价结果一般停留在国家宏观层面。此外，在之前的研究中，对于指标体系权重的计算方法或采用主观计算或采用客观计算，后来也有将主观权重和客观权重相结合计算组合权重的研究，但是往往只是进行简单的加法或乘法计算。因此，有必要站在国际工程项目的视角下，研究政治风险在工程项目实施过程中对项目的影响机理，建立相应的评价体系并对其进行科学评估，从而为我国国际工程承包商进行有效的政治风险管理提供科学的依据。

文章选用模糊综合评价法进行国际工程政治风险的评估。在分析“国际工程”、“政治风险”两个层面元素特点的基础上，识别并优选了国际工程政治风险评估指标，建立了结合政治风险相关特定风险因素的风险指标体系，使得风险指标体系更加完备且更具针对性与应用价值。同时，为了能更准确、科学的计算风险指标的权重，全面反映指标体系的主观差异和客观差异，文章选择运用组合赋权法，即分别采用AHP法和熵值法确定各层指标的主客观权重，将主观赋权法与客观赋权法相结合，这样既能反映出工程风险因素内在的客观规律，又能反映出项目人员对工程的认识以及其主观意愿，并将距离函数引入到指标权重的计算中，充分考虑了主观权重与客观权重的影响关系，使指标权重的计算更为准确。

1 国际工程政治风险评价指标体系建立

1.1 国际工程政治风险影响因素分析

国际工程政治风险的影响因素众多且较为复杂，每个影响因素对于工程项目的影响程度不同，国内外风险评级机构以及风险管理专家、学者通过实例分析、理论研究等方法对影响政治风险的因素进行了研究和分析。统计、归纳和分析现有学者的研究成果，统计具有代表性的论文和影响因素，见表1[6－15]。

分析表1可以得到，战争与内乱风险所占百分比为84.6%，学者普遍认为其属于政治风险范畴，且风险发生可能性高、影响性大，因此文章将其在政治风险范围内考虑;其次，政府更迭风险与征收风险所占比例并列第二，均为53.8%。其中，政府更迭是指东道国政府的稳定程度，它受很多因素的影响，但最终与东道国执政党的实力、在野党的数量和各党派关系等因素相关，且相对其他因素独立，因此文章将其作为政治风险的影响因素之一。另外，征收风险、违约风险、政策法规变化风险、政府干预风险等虽然所占百分比并不高，但文章认为这几项影响因素本质上均与东道国政府的信誉度相关，因此将这几项因素合并为政府信誉度风险。对于得分较高的法律风险，由于其本身相对于其他风险因素较为独立，此处认为其因单独作为一项与政治风险并列的风险考虑，故文章不将其作为政治风险考虑在内。其他统计百分比在15.4以下的影响因素可暂不在政治风险因素内考虑，其余因素将作为建立指标的依据。

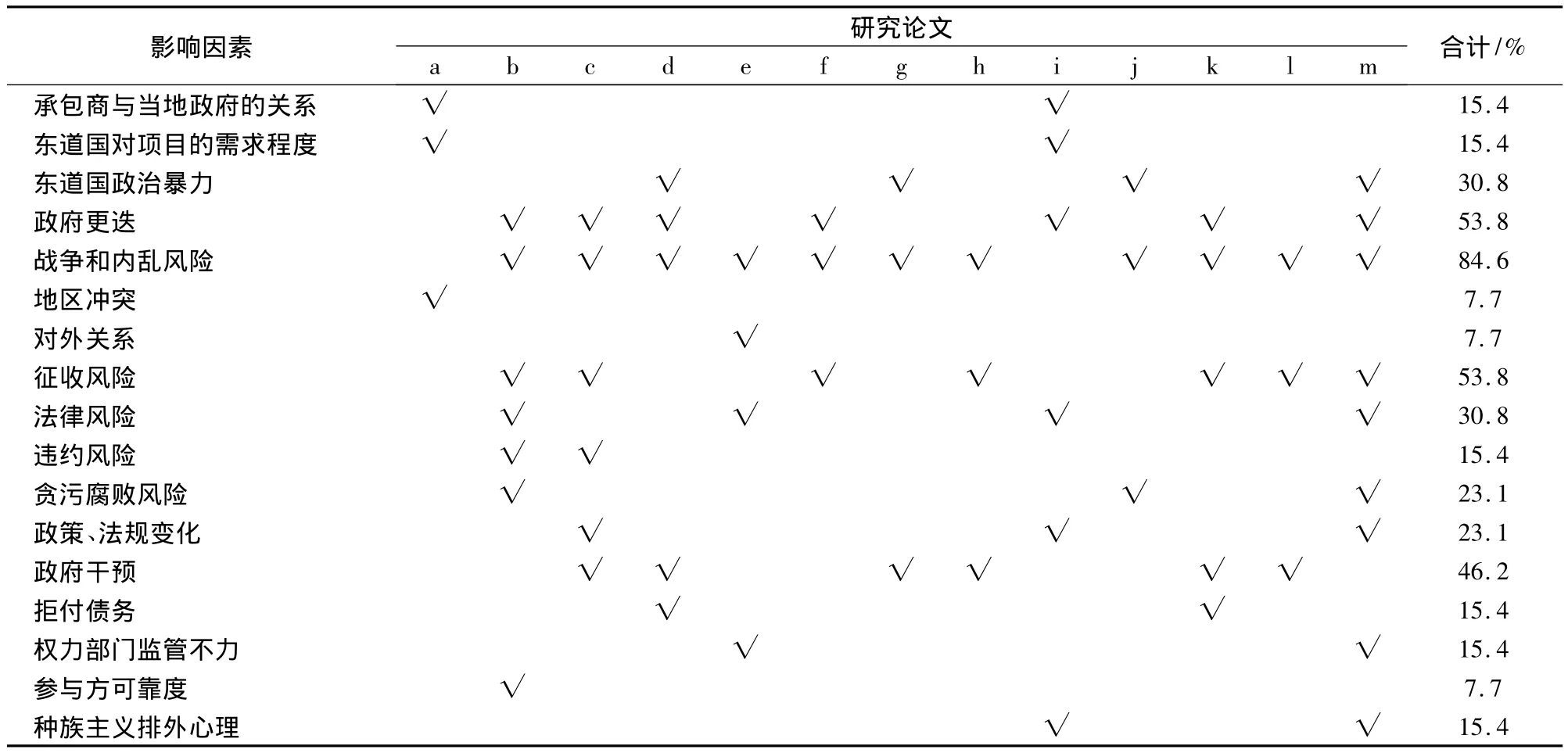
表1 国际工程承包政治风险影响因素分析表

1.2 国际工程政治风险指标体系确定

根据政治风险影响因素分析结果，文章将政治风险的影响因素分为征收风险、违约风险、贪污腐败风险、政策法规变化风险、政府更迭、政治暴力、政府干预这七项影响因素。其中，征收风险、违约风险、政策法规变化、政府干预这几项因素属于政府行为范畴，而这些政府行为可能带来的风险均是由政府信誉度导致的，因此将这几项因素用政府信誉度来表征;政治暴力是造成政府更迭的因素之一，因此将其与政府更迭合并，用政府稳定度来表征;政府贪污腐败相对其他风险影响因素较为独立，因而单独以政府腐败程度来表征;战争以及局部动乱反映了一国社会安全的稳定程度，因此用社会安全程度表征;此外，国际工程大多要与当地政府打交道，且货物的运输、文件的审批等均需通过当地政府机构审核，因而东道国政府机构的办事效率也直接影响工程的工期、成本等，故将其作为指标之一。

综上所述，同时结合相关领域专家学者的建议和意见，将政治风险影响因素归纳为政府稳定性、政府信誉度、政府腐败程度、政府机构办事效率以及社会安全程度这五类一级指标，具体指标体系如图1所示。

图1 政治风险评价指标体系图

2 国际工程政治风险评价模型构建

2.1 风险评价模型的建立

在国际工程政治风险评价指标体系的基础上，利用层次分析法，建立如表2所示的政治风险评价指标体系，并用模糊综合评价法对其进行综合评判。

表2 基于AHP的国际工程政治风险评价指标体系

2.2 风险指标权重的确定

为了能更准确科学地计算风险指标的权重，全面反映指标体系的主观差异和客观差异，文章选择运用组合赋权法计算权重，主观赋权法采用层次分析法(AHP)，客观赋权法采用熵值法。

2.2.1 AHP 法确定主观权重

首先根据指标体系确定层次分析结构;构造判断矩阵，计算要素相对权重。AHP方法要求决策人给出因素不同组合下的总体评价，这里，采用将因素成对比较，第项因素相较第项因素重要程度的比较值记为，采用表3中所列方法进行取值。

表3 九标度法

aij近似地就是两两比较因素的权重比值，最终，n项因素成对比较的结果可用比较矩阵来表示，由此得到

由该矩阵决策者可以计算出各因素的权重值，即权向量。确定权向量方法众多，文章将采用和法来确定权向量，由式(1)表示为

式中:wi为因素的主观权重值;aij为名因素两两比较的权重比值;n为因素个数。邀请不同领域相关专家(风险管理专家、教授、政治经济学家等)若干名，针对上一节中建立的风险评价指标体系中各级风险影响因素进行对比评价，然后根据专家的反馈结果，按照上面的方法计算出风险各项指标的主观权重。

2.2.2 熵值法计算客观权重

在系统学理论中，信息熵 H(x)－∑P(xi)lnP(xi)反应了系统的不确定性程度。风险评估过程中，某项指标的信息差异程度越大，该指标的信息熵越小，指标的权重越大。在国际工程政治风险研究中，通过与模糊法进行风险评估相结合，将风险指标的分类作为评语，利用隶属度作为概率值，从而进一步计算风险指标的熵值。

(1)构造模糊隶属度矩阵

对指标因素集中的因素ui(i=1，2，…，n)作单因素评判，设其对决策等级vj(j=1，2，…，m)隶属度为 rij，得出 ui按因素的评判集 ri=(ri1，ri2，…，rim)，分别按n个因素评判后可构造出评价矩阵R由式(2)表示为

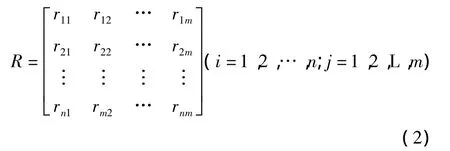
(2)计算指标熵值

计算各个指标的熵值ei由式(3)表示为

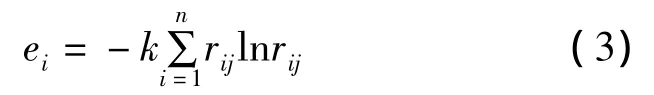
式中:ei为各指标熵值;rij为指标隶属度;k为比例系数。

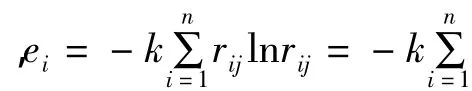
则，式(4)可表示为

(3)计算指标熵权

各指标之间的差异系数由式(5)为

各指标的熵权由式(6)表示为

2.2.3 确定组合权重

一般常见的几种组合权重的方式(包括加法式、乘法式和加权式)不能将不同方法计算出的权重之间的差异准确的表示出来，为了使指标权重与不同方法计算权重的分配系数相符合，引入距离函数，进行主观权重与客观权重的组合。

设主观权重w1与客观权重之间的距离函数由式(7)表示为

对主观权重w1与客观权重w2进行线性加权，得组合权重由式(8)表示为

式中:α、β分别为w1与w2的分配系数。

为了使不同权重之间的差异程度与分配系数之间的差异系数一致，则存在式(9)、(10)为

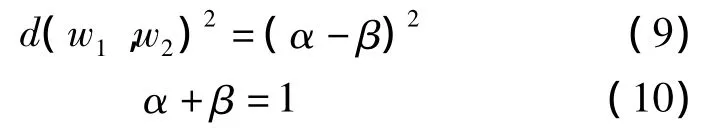
根据上述公式，可求得不同权重的分配系数，进而求得指标的组合权重。

2.3 风险模糊综合评价

文章构建二级模糊综合评价模型对其风险大小进行评价。

(1)确定评价因素集合

评价因素集是指国际工程政治风险指标体系中影响政府稳定度、政府信誉度等五项指标下的二级指标所组成的集合，用U表示，即U={u1，u2，…，un}

(2)建立评价评语集合

评价评语集是邀请的风险管理专家根据各层风险指标的具体情况所产生结果可能性的判断，用V表示，即 V={v1，v2，…vn}

(3)确定因素权重集合

国际工程政治风险各指标的组合权重集合即为因素权重集合，用 W 表示，即 W={w1，w2，…，wn}

(4)确定评价隶属度矩阵

首先对国际工程指标体系中指标层进行评价，分别确定各分指标在以指标层为准则时对评语集的隶属度。隶属度判断结果可表示为Ri:Ri={ri1，ri2，…，rm}

对各因素重复上述步骤，最终得到一个总的评价矩阵R

其中，该模糊矩阵中的每一项元素均表示第i个因素ui在第j个评语上的频率分布，并使其满足∑rij=1。这样R就已经被量纲化了，不需再做专门处理。

(5)模糊综合评价

根据权重集和隶属度矩阵，计算模糊综合评价评价集由式(12)表示为

式中:B为政治风险所有因素的影响，得出的三个一级指标的隶属度。

(6)最终计算结果。

设定评判集V中各元素以具体数值，用xi表示

用公式 Pi=BiVT(13)计算得 Pi{i=1，2，…，n}。

按照上述步骤，完成国际工程政治风险评价指标体系中的各指标层的模糊评价，再将计算结果作为已知值，对目标层进行一次模糊评判，从而得出国际工程政治风险的大小水平。

3 国际工程政治风险评价算例应用

3.1 国际工程政治风险评价算例概况

SA水利枢纽工程位于苏丹东部K州与J州的交界处，由两座大坝及其附属工程组成，主要功能为灌溉、供水，兼顾发电。该项目有苏丹政府融资，通过公开招标，由中国SS集团与其下属子公司DD公司组成的联营体进行总承包。中国SS集团通过搜集资料了解到苏丹基本政治情况。2011年，南苏丹宣布独立，南北双方在边界划分、居民国籍认定、石油利益划分等问题上冲突不断，2012年4月苏丹总统巴希尔对南苏丹宣战，誓言推翻苏丹人民解放运动领导的南苏丹政权，两国局势紧张，冲突升级，反政府武装行动时有发生，社会动荡不安，给工程造成极大威胁。政局混乱的情况下，苏丹政府机构办事效率急剧降低，立等可取的事情往往需要花费几天甚至更长的时间。

3.2 国际工程政治风险评价算例分析

3.2.1 国际工程政治风险指标体系建立

对SA工程政治风险进行识别后，结合文章第一节的研究，建立风险评估指标体系见表2。

3.2.2 国际工程政治风险指标权重计算

(1)指标数据收集

文章选用五种评语结果，即V={高度风险，较高风险，中度风险，较低风险，低度风险}。根据已构建的评价指标体系和评语集，设计调查问卷并向25位专家进行发放，通过聚类分析法，最终筛选出19位专家的打分意见，包括判断矩阵评语集统计，表4至表9为判断矩阵表，表10为专家评语集统计表。

表4 目标层判断矩阵

表5 政府稳定度判断矩阵

表6 社会安全度判断矩阵

表7 政府信誉度判断矩阵

表8 政府机构办事效率判断矩阵

表9 政府腐败程度判断矩阵

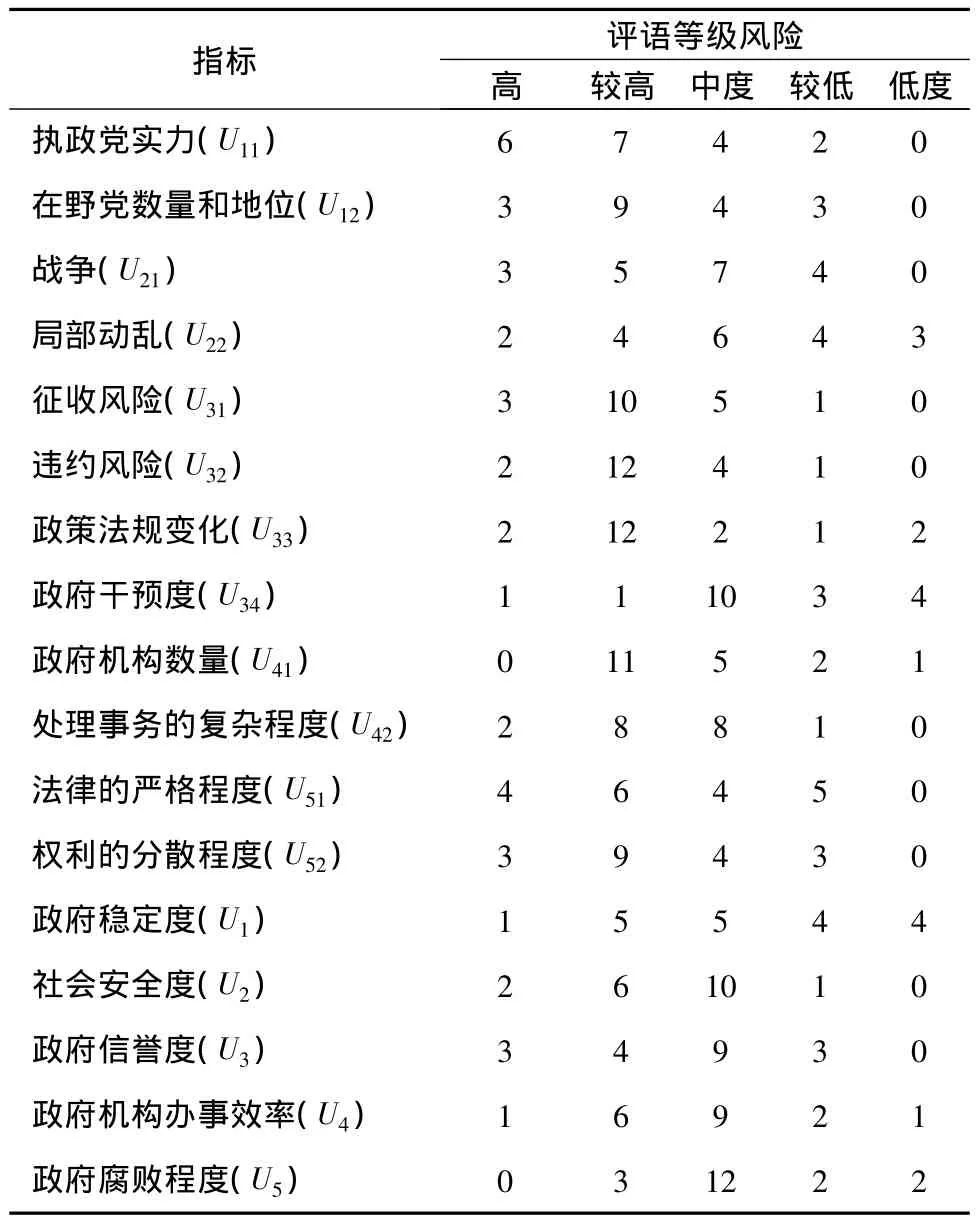
表10 指标体系专家评语集统计

(2)指标权重计算

根据2.2节中确定的权重计算方法，分别计算出指标的主观权重和客观权重，并最终计算出各指标的综合权重，最终的指标权重计算结果见表11。

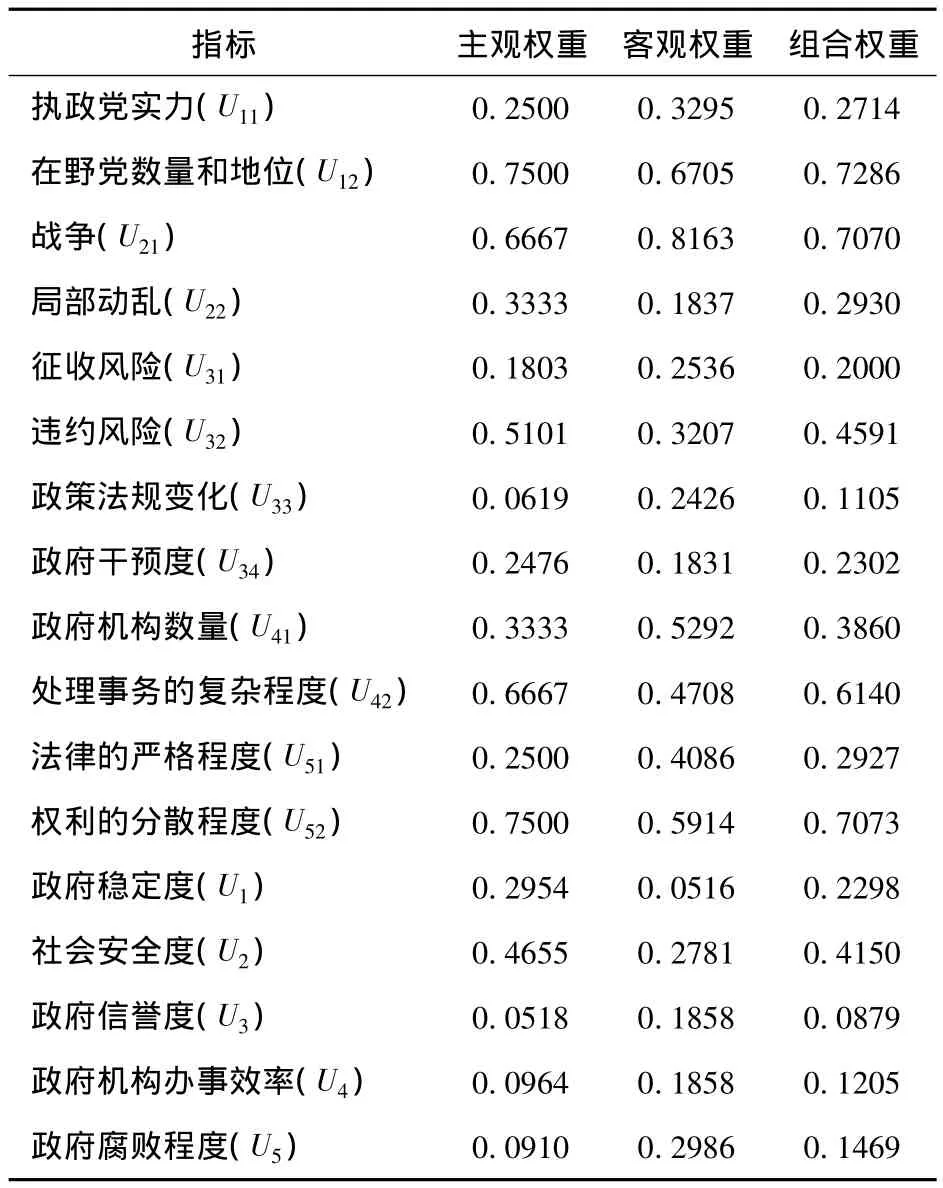
表11 国际工程政治风险指标权重计算统计表

3.2.3 国际工程政治风险模糊综合评价

(1)指标层模糊综合评价

根据专家对指标评语，分别建立指标层模糊评价隶属矩阵，分别得到政府稳定度风险因素R1、社会安全度风险因素R2、政府信誉度风险因素R3、政府机构办事效率风险因素、政府腐败程度风险因素评判隶属矩阵为

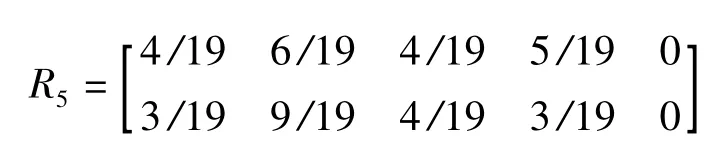
根据上节计算的组合权重，得指标层权重矩阵为

根据组合权重和隶属度矩阵，对指标层进行模糊综合评价为

(2)目标层模糊综合评价

用以上计算结果构造国际工程政治风险总体大小的评价矩阵，即得到

因此，国际工程政治风险模糊综合评价结果为

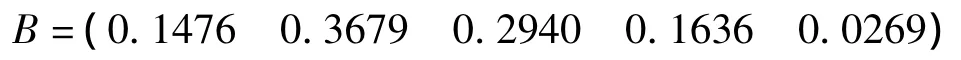
将结果归一化处理后得

(3)计算最终结果

设定评判集V中各元素具体数值:

用公式Pi=BiVT计算为

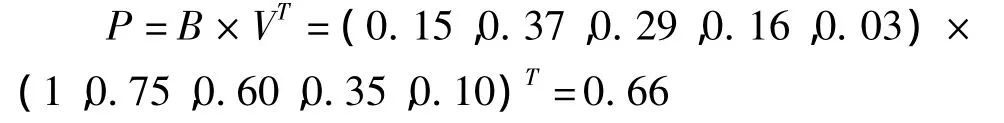
同理，

P1=0.71 P2=0.62 P3=0.70 P4=0.67 P5=0.69，详细评断结果见表12。

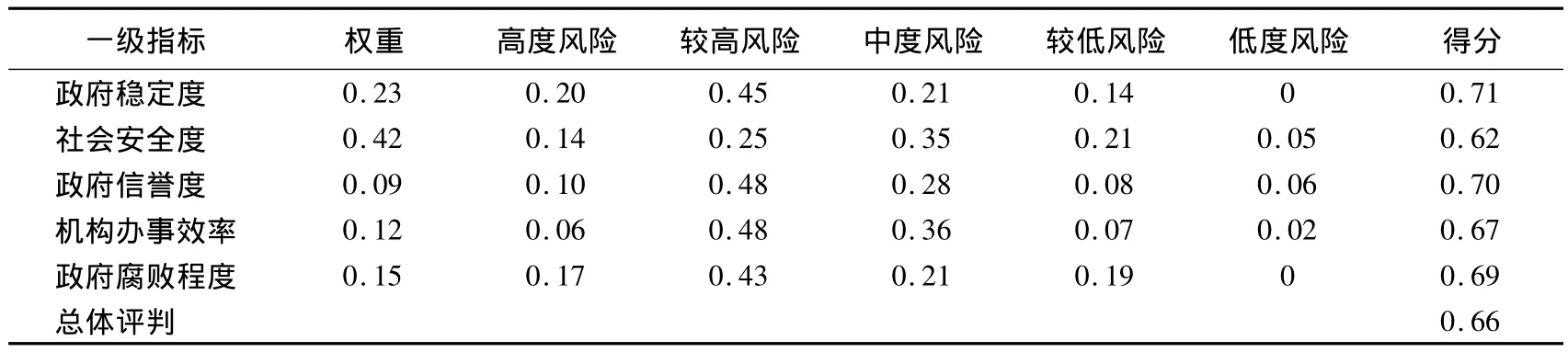
表12 SA水利枢纽工程政治风险算例分析结果

分析以上各表中数据，可以总结为

(1)本算例中国际工程政治风险总体评价得分为0.66，因 0.6 ＜0.66 ＜0.75，因此，可以判定本算例中的政治风险属于较高风险。

(2)本算例中政府稳定度风险因素得分为0.71，表示此项风险属于高度风险，而政府稳定度风险属于承包商不可控风险，因此，承包商在进入该国之前应当及早评估并购买相应保险进行应对。

(3)本算例中在确定政治风险各因素进行权重确定时，将主观权重和客观权重进行了综合，相对来说增加了评价结果的科学性。

3.2.4 国际工程政治风险应对措施建议

目前为止，我国国际工程承包多在非洲、中东等社会环境复杂、政治局势不明的区域，政治风险对承包商的影响较大。对于一般政局较混乱区域的工程或者对政治风险较敏感的承包商，一般采取风险规避的方式，在充分分析项目所在国政局及政府信誉等问题后，选择放弃项目。而对于已进行的项目而言，可选用以下措施防范一部分政治风险。

(1)在项目开始前应充分考虑政治风险发生的可能性及其可能产生的损失，尽量与政府签订担保协议，明确界定政府、业主部门与项目公司的责任划分，一旦政治风险发生，可按担保协议向政府要求承担一部分损失或者给予一定的赔偿。

(2)通过投保的方式进行风险转移是国际承包商应对政治风险最常用的措施。可根据公司对政治风险的评估以及自身能力与需求，向中国出口信用保险公司或世界银行多变投资担保机构(MI-GA)投保违约、战争和内乱等政治险，将风险转移给第三方。

(3)大力寻求当地的军方保护，同时建立完善的安保制度。对于战争或局部动乱发生概率较大的地区，可与当地军方沟通，寻求保护;另一方面，应加强工地的安保措施，并加强员工的安全培训，设立严格的人员外出管理制度，从而尽可能的控制战争、动乱等可能造成的人员伤亡与财产损失。保护费用应在投标报价中加入成本估计。

SA水利枢纽工程的政治风险是较高风险级别，建议优先采用风险转移的应对方式，承包商可在投保基本险的基础上，投保战乱险，应对战乱可能造成的机械、材料等货物的损失;另外，鉴于政局不稳定局势，SA工程与苏丹政府签订协议时可加入触发型条款，将部分战乱风险通过政府担保的形式转移给政府;另一方面，设立严格的人员外出管理制度，加强出入门登记制管理，并加大安保投入，在一定程度上减少人员受损的可能性。

4 结语

政治环境的复杂、国际经济形势的多变、地域文化的差异以及陌生的自然环境等都给国际工程承包带来了更多的不确定，对国际工程承包企业的风险管理提出了更高的要求。政治风险由于其属于宏观层面风险，是承包商难以控制的风险因素，且其一旦发生，将会给承包商带来巨大的经济损失。文章针对国际工程政治风险建立了比较完整可行的风险评估体系，实现了风险指标体系的建立、指标权重的确定以及风险最终的综合评估。相关研究成果有助于承包商实现国际工程政治风险的有效应对，保障工程顺利进行的同时，提高企业经济效益与竞争力。

[1]王宗敏.我国国际工程承包风险管理研究[D].南京:河海大学，2007.

[2]侯静.国际工程承包风险管理研究[D].北京:北京交通大学，2012.

[3]Kesternich I.，Schnitzer M..Who is afraid of political risk multinational firms and their choice of capital structure[J].Journal of International Economics，2010，82(2):208 －218.

[4]蔡强.项目视角下的国际工程项目政治风险评价—基于灰色关联分析和二元语义评价组合模型[J].项目管理技术，2013，11(11):71 －76.

[5]Deng X.P.，Low S.P..Understanding the critical variables affecting the level of political risks in international construction projects[J].Journal of Civil Engineering，2013，17(5):895 －907.

[6]胡文发.基于BP算法的国际工程项目政治风险评价模型[J].重庆建筑大学学报，2006，28(4):99－105.

[7]宋金刚，李刚，颜瑛.国际工程项目政治风险的管理控制策略[J].经济师，2011(4):81－83.

[8]王雪青，何贞.国际工程项目风险评价指标体系及模型构建研究[J].山东建筑大学学报，2013(2):112－123.

[9]牛学辉.新形势下国际工程承包风险问题研究—以利比亚危机下中国工程承包企业风险为例[J].宏观经济，2011(10):33－37.

[10]李凤升，温丽，孙彦彬.石油企业国际工程项目风险评价 —基于层次分析法[J].辽宁工程技术大学学报(社会科学版)，2011(3):265－268.

[11]薛铁柱.国际工程承包中的风险管理[J].企业导报，2010(7):109－110.

[12]范体军，张莉莉，常香云.我国海外石油开发利用的国家风险评估[J].管理学报，2011，8(6):943－948.

[13]聂名华.中国企业对外直接投资风险分析[J].经济管理，2009(8):52－56.

[14]Deng X.P.，Low S.P..Understanding the critical variables affecting the level of political risks in international construction projects[J].Construction Management，2013，17(5):895 －907.

[15]吕哲.中国国际石油合作中政治风险的指标体系构建与规避措施的研究[J].华商，2007(12):11－13.