基于MATLAB仿真的碳纳米管建模分析

马　俊，张　勇，邓中民

（武汉纺织大学 数学与计算机学院，湖北 武汉 430200）

基于MATLAB仿真的碳纳米管建模分析

马俊，张勇，邓中民

（武汉纺织大学 数学与计算机学院，湖北 武汉 430200）

碳纳米管模型的建立是纳米纤维研究的基础。探讨基于M ATLAB仿真的碳纳米管建模的效果，主要从碳纳米管中碳原子之间的几何关系出发，确定最小重复单元中所有碳原子在直角坐标系下的几何坐标，再利用坐标变换，得到满足要求的碳纳米管模型。结果表明：M ATLAB仿真效果良好，能得到满足要求的碳纳米管模型。

碳纳米管；M ATLAB；几何关系；重复单元；坐标变换

碳纳米管自被发现以来，一直被公认为是人们所能制造出来的最强、最刚、最韧的分子，是最好的热和电的分子导体，在诸多领域具有广阔的应用背景[1]。为了更好地实现碳纳米管的优良性能和诸多实际应用，可将碳纳米管组装成宏观材料，如纤维。近年来已经通过向合成纤维聚合物中添加某些亚微米级或纳米级无机粉末的方法，经过纺丝获得具有某种特殊功能的纤维。随着纳米材料制备合成技术的不断发展和纳米材料基础理论的日趋完善，纳米纤维的应用将遍及纺织等工业的各个领域，它对纺织品及其它领域的研究开发的促进作用将是无法估量的。同时，碳纳米管独特的光学、力学、电学和热学特性吸引了物理、化学、材料、电子等多个领域专家的极大关注。但不管在哪个研究方向上，碳纳米管模型的建立都是整个研究过程的基础。

目前主要运用分子静力学法建立了碳纳米管模型，首先生成一个正六边形，以六边形为单位循环得到一层排列类似于石墨的晶格结构，再在一定条件下对晶格点坐标进行截断，最后利用投影法得到碳纳米管，过程较为繁琐[2]。本文按由浅入深的方式研究问题，先对平面碳纳米管建模分析，然后将其思路迁移到空间碳纳米管，主要从碳纳米管各个点的几何关系出发，详细分析碳纳米管中原子之间的关系，运用MATLAB仿真，建立碳纳米管模型，方法简单，易于理解。结果表明：MATLAB能够将空间碳纳米管形象的展现出来。

1　平面碳纳米管建模分析

1.1基本构成单元

由于碳纳米管的规则结构，本文采用化整为零的思想，先研究构成碳纳米管的基本结构单元。如图 1所示为基于MATLAB的碳纳米管的基本结构单元的模拟图。利用MATLAB构造自定义函数cylinder2P.m来完成两个已知点的连接，即仿真碳碳键。图 1(a)为碳碳键的仿真图，对于给定的两个已知点，使用cylinder2P.m函数即可产生一根圆柱将两点连接。同时，自定义函数draw_ball.m完成已知点的描述，图1(b) 为A、B碳原子的仿真图，故对于给定的点，即可利用draw_ball.m函数在该点处画一个球表示该点。图1(c)则为在图1(a)和图1(b)的基础上，同时运用cylinder2P.m和draw_ball.m函数，将碳原子连接起来。

图1　基本结构单元模拟

1.2最小重复单元建模

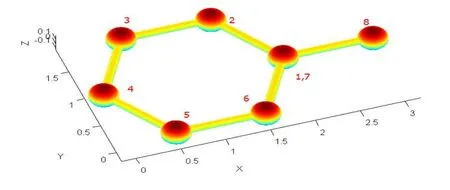
图2　最小重复单元模拟

考虑到碳纳米管的规则分布，选择其最小重复单元分析即可得到整个结构。基于这种思想建立如图2平面直角坐标系，选取最小重复单元为8个碳原子，考虑后续依次连接问题及正六边形的封闭性，将第1点同时标记为第7点。最小重复单元结构如图2所示，为一个正六边形和一个碳碳键组成，加上一个碳碳键是为了方便前后两个正六边形的连接。设碳碳键的长度为ac- c, 对于空间正六边形，则8个点的坐标如表1所示。

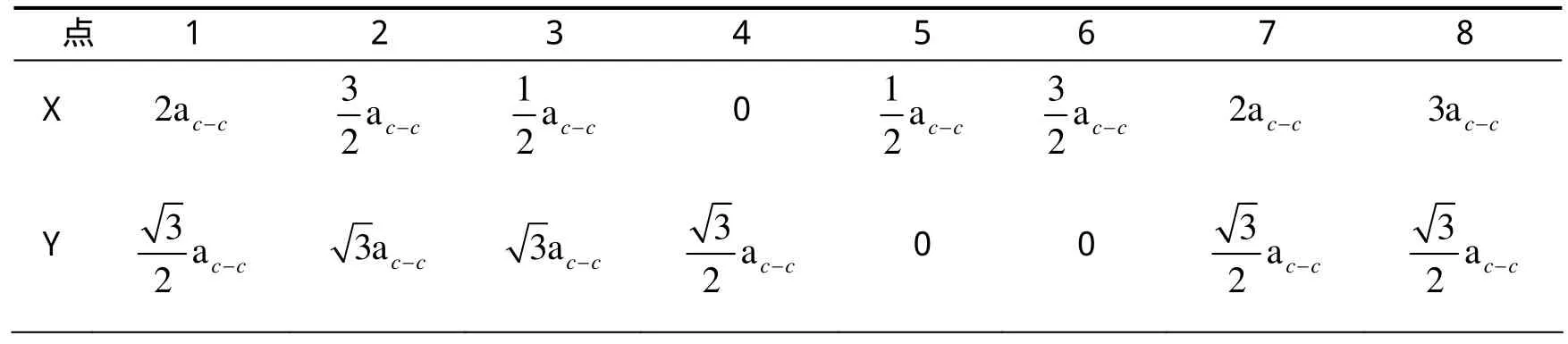
表1　最小重复单元各点坐标

1.3平面碳纳米管的连接次序

在最小重复单元的8个点坐标确定以后，下面关键的就是将点的坐标依次连接起来。连接次序如图2所示，由连接次序可知，第1点和第7点重合。

1.4最小重复单元延拓成完整碳纳米管

平面碳纳米管呈网状分布，因此在获得最小重复单元的基础上，通过坐标的平移变换，将最小重复单元进行延拓，从而获得整个平面上的碳纳米管。坐标平移公式如(1)所示。

其中a，b分别为x和y方向上的平移增量。

故为了获得平面碳纳米管网状结构，可在最小重复单元的基础上运用坐标平移变换，在x正方向上每一次延拓，横坐标都要增加3ac- c，在y正方向上每一次延拓，纵坐标都要增加3ac- c。图3所示为坐标平移变换后得到的平面碳纳米管的模拟示意图。

图3　平面碳纳米管的模拟

2　空间碳纳米管建模分析

2.1空间最小重复单元建模

完成了平面碳纳米管的模拟，进一步的研究重点将是空间碳纳米管的建模。目前已有研究认为，可在平面碳纳米管的基础上，利用投影法将平面碳纳米管映射到半圆柱面上，然后利用对称变换得到完整的空间碳纳米管，但过程较为繁琐，且边界缝合情况存在不足[3]。空间碳纳米管建模与平面碳纳米管建模有一定的联系，将平面碳纳米管的建模思路迁移到空间碳纳米管建模将是一个很好的选择，依然选择对最小重复单元建模的方式。

图4　碳纳米管的一个最小重复单元

如图4所示本文选取的碳纳米管一个最小重复单元，该重复单元可分为上下两层，记为A层和B层。各层都是由碳原子按一定规律分布在圆环上，观察图4可发现规律为，对于每一层，记碳碳键的长度为 ac- c，相邻碳原子之间的距离依次为 ac- c和2ac- c循环交替出现，即可对每一层建立如下数学模型。如图5所示，先对第一层碳原子建模，确定其坐标关系[4]。

图5　第一层碳原子建模

第一层碳原子的圆心O为坐标原点，过原点和键A2n—A1的中点C的直线为X轴，垂直于第一层碳原子所在平而的轴线方向为Z轴，建立相互垂直的三维坐标体系XYZ，见图5。

设碳纳米管的半径为R，L为圆周长， ac- c为碳碳键长度。为了简化计算，本文近似的以所有连接2n个点的线段作为圆周的长度，即。由求得

在△COA1中，设∠COA1=α，由于，，可求得

在△A1OA2中，由于，设，则。

则A1点的坐标值为。

则A2点的坐标为=0

A3的坐标为，所以

A4点的坐标

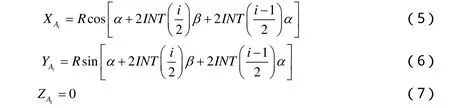
式中：INT()为求整函数。由式(2),(3),(4)知，当（n, n）型碳纳米管的n值确定后，R，β，α 都为确定的常数值，从而 Ai的坐标值得以确定。

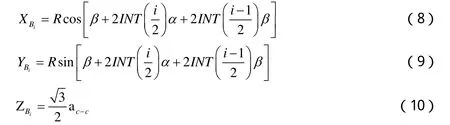
2.2空间碳原子连接次序分析

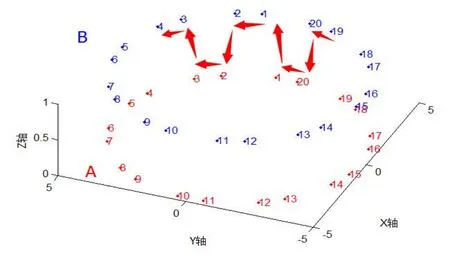
图6　空间碳原子连接次序示意图

由坐标公式(5)-(10),可以确定最小重复单元中A层和B层碳原子的坐标，坐标确定后各点间的连接次序是又一关键问题。为了便于观察，取n=10,如图6所示，先依次将A层和B层中坐标点标号，红色表示A层，蓝色表示B层。根据图4中碳纳米管的最小重复单元仿真图，同时为了方便MATLAB的程序编写，本文选取A层和B层的连接次序示意图如图6所示，具体的如表2所示。运用MATLAB,构造自定义函数linka_b.m，将A层和B层中的点按表2的顺序构造成一个联合矩阵，然后运用自定义的cylinder2P.m函数循环将联合矩阵中所有的点连接起来即可，效果如图4。

表2　空间碳原子依次连接顺序

2.3最小重复单元延拓成完整碳纳米管

在建立最小重复单元模型的基础，利用坐标的对称和平移变换来得到整个空间的碳纳米管的结构，空间坐标变换公式与平面坐标变换公式相似[5,6]。实验结果如图7所示。

图7　逐层模拟碳纳米管

3　结束语

建立碳纳米管模型是模拟研究碳纳米管结构、性能及各种应用的基础。本文按由浅入深的方式研究问题，先对平面碳纳米管建模分析，然后将其思路迁移到空间碳纳米管。具体建模过程中，主要根据碳纳米管自身的结构特点，首先确定一个最小重复单元中碳原子的坐标，然后按照一定次序依次连接各点，最后根据坐标变换，延拓出完整的碳纳米管模型。实验结果表明，利用MATLAB对碳纳米管进行建模仿真，不仅能够仿真平面碳纳米管，而且能够将空间碳纳米管形象的表示出来。由于仅从碳纳米管中碳原子的几何结构出发建立模型，故方法简单，易于理解，且所建模型形象逼真，为进一步模拟研究做好准备。

[1] 郭连权，马贺，等．碳纳米管结构的模拟计算[J]．沈阳工业大学学报，2005，27(4)：466-469．

[2] 程锦荣，闫红，陈宇，等．碳纳米管储氢性能的计算机模拟[J]．计算物理，2003，20(3)：255-258．

[3] 王积森，张洪云，等．分子模拟中碳纳米管模型建立原理分析[J]．纳米材料与结构，2006，11：520-524．

[4] 蒋玲玲，陈小泉．纳米纤维素晶体的研究现状[J]．纤维素科学与技术，2008，16(2)：73-76．

[5] 王能，丁恩勇，程镕时．纳米维晶纤维素表面改性研究[J]．高分子学报，2006，11(8)：982-987．

[6] 朱宏伟，吴德海，徐才录．碳纳米管[M]．北京：机械工业出版社，2003．41-61．

Analysis of Modeling the Carbon Nanotubes Based on MATLAB Simulation

MA Jun, ZHANG Yong, DENG Zhong-min
(School of Mathematics and Computer Science, Wuhan Textile University, Wuhan Hubei 430200, China)

Carbon nanotubes model is the foundation of nanofiber research. MATLAB simulation was discussed. The study is mainly from the geometric relationships between the carbon atoms of carbon nanotubes, determined the coordinate geometry of the minimum repeat unit under the rectangular coordinate system. Then using coordinate transformation, model of carbon nanotubes could get well. The results show that MATLAB simulation effect is good, which can satisfy requirements of carbon nanotubes model.

carbon nanotubes; MATLAB; geometrical relationship; repeat unit; coordinate transformation

O799

A

2095－414X(2015)06－0045－05

马俊（1963-），男，教授，博士，研究方向：小波理论及其应用.