基于改进的Logistic混沌映射彩色图像加密算法

黄 硕

(信阳职业技术学院 数学与计算机学院，河南 信阳464000)

图像加密是保护图像安全的一种直接有效的手段，众多学者对图像加密技术做了大量研究并取得了丰富的成果，如基于现代密码体制的图像加密、基于矩阵变换的图像加密、基于混沌的图像加密、基于分存的图像加密、基于频域的图像加密、基于SCAN语言的图像加密和基于DNA计算的图像加密等［1］.针对彩色图像加密设计，需要考虑以下四点基本要求:加解密速度快、Kerckhoff原则、密钥空间大、解密保真度高.根据这四点基本要求，在不需要压缩加密的前提下，应该尽量选择在RGB色彩模型空间或空域上进行，并综合考虑运行速度、抗攻击能力、密钥空间大小、抗噪声及抗剪裁能力等因素来设计加解密算法.因此，针对密钥情况提出了一种改进的、具有较大密钥空间的Logistic混沌映射来产生混沌密码序列;针对加密算法在序列异或加密算法上进行改进，以避免单纯异或加密的缺点，同时又保留了加解密速度快的优点;针对加密效果，通过实验仿真，并从直方图、加密效果评价参数、抗剪裁、抗噪声、相关性、密钥空间大小等方面进行了深入分析.

1 传统的Logistic算法分析

Logistic映射方程来自现实中的人口统计，是典型的非线性用来描述混沌状态的方程，能够简单地表现混沌运动的一般特征.传统单一性的Logistic算法过程如下:①挑选恰当的Logistic方程生成密钥序列的算法;②输入作为加解密初始密钥的初值;③从目前所处的轨迹启动迭代程序;④形成混沌运动的实数序列，将这些序列转化为方便处理的二进制序列;⑤将其中某部分的明/密文选为带加/解密明文;⑥用异或运算来处理所得到的二进制序列与当前的待加密明文/待解密密文，结果为密/明文序列;⑦将目前运算的行踪作为下一次加/解密的初始密钥;⑧对加/解密是否完成进行判断，没有完成则返回到第③步;⑨加/解密完成.

传统的Logistic加密算法方便快捷、便于实现，并且由于混沌系统本身对初值比较敏感，又有随机性，这使得传统的Logistic算法具有一定的安全性.但是，传统的Logistic算法缺点也非常明显，主要有以下几点:

(1)通过试验总结出来的混沌序列的周期、伪随机性和复杂性，很难保证这些参数都足够高;

(2)为了保证一样的周期，混沌函数内部所使用的存储器数目是寄存器的两倍;

(3)混沌序列发生器使用的是有限精度器，有限的精度是实际应用混沌序列的一大障碍.

其中，缺陷(3)非常突出，故基于此对传统的Logistic系统进行了改进.

2 改进的Logistic混沌映射

Logistic映射是用得最广的一种混沌系统，其定义如下:

其中，0＜μ≤4称为分支参数，xk∈(0，1)，当3.569 946＜μ≤4时，Logistic映射处于混沌状态，也就是说初始条件x0在Logistic映射的作用下所产生的序列{xk}是非周期性的、不收敛的并对初始值非常敏感.因此，若仅仅用以上一维Logistic混沌映射来产生混沌密码序列已不够安全，极易暴露混沌系统的相关信息.为了提高系统的混沌程度，张靓［2］提出了一种改进的二维Logistic混沌映射，如下式所示:

当3.81≤u≤3.815时，其最大Lyapunov指数在2.2左右，该映射处于混沌状态.但是，根据Kerckhoff原则，要求密钥空间尽可能大，为了增大式(2)Logistic混沌映射的混沌度，结合Chebychev混沌映射，如下式所示:

对式(2)所示的Logistic混沌映射的参数μ进行扰动，即μ不再是一个定值，而是随Chebychev混沌映射的值而动态地变化.

当参数k=6时，Chebychev系统的Lyapunov指数为1.791 733…，映射处于混沌状态且zn∈［-1 1］.由此，可构造新的参数μ的表达式，如下式所示:

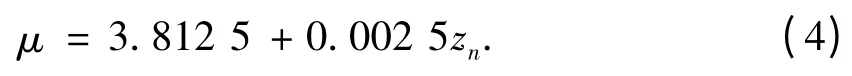
从而，式(2)变成了式(5)，即为本算法所提出的改进的Logistic混沌映射:

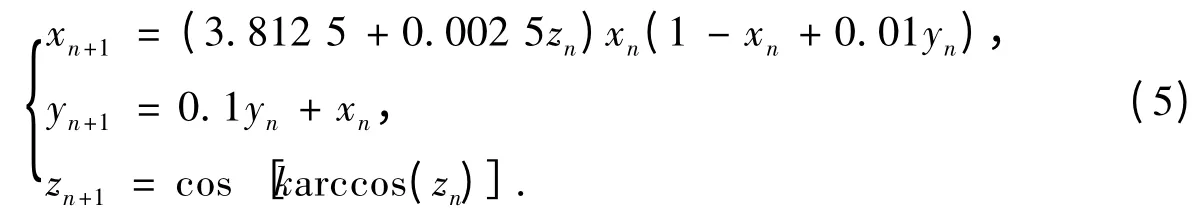
通过Matlab编程，当x0=0.345 678，y0=0.578 993，z0=0.234 567时，式(5)在迭代1 000次后的三维散点图如图1所示.在迭代100万次后，统计得到xn，yn，zn的值域(只显示16位有效数字)分别如下:

同时，通过Matlab中的tabulate函数对xn，yn，zn进行了频数统计，发现每一个值都只出现了1次，表明所提出的Logistic混沌映射系统能产生较高随机性的3组混沌序列.

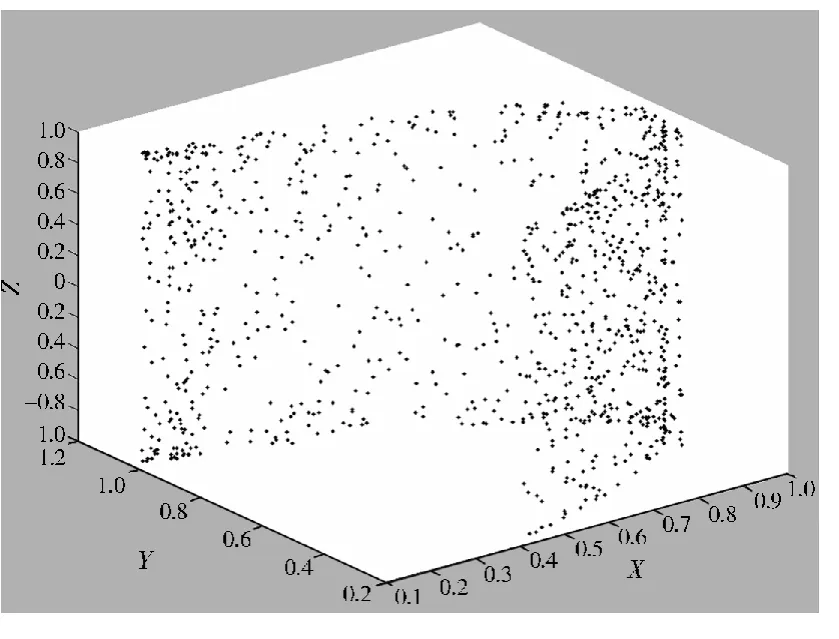
图1 迭代1 000次后的三维散点图Fig.1 Three-dimensional scatter plot after iteration 1 000 times

3 加解密算法描述

针对一幅M×N的24位真彩色图像，共有M×N个像素和M×N×3个灰度值.鉴于图像异或加密的简单性与快速性，将其进行改进，提出一种新的加解密算法，整体流程如图2所示.

加密步骤如下:

(1)输入密钥x0，y0，z0和I，其中x0，y0，z0分别为式(5)所示混沌映射的初始值，I为混沌序列的初始迭代次数.然后，产生两组长度为M×N×3的一维混沌密码序列SX和SY，其产生方式如下式所示:

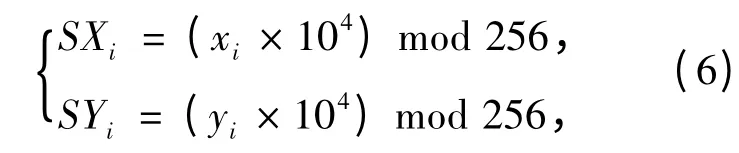
其中，i∈［1 M×N×3］，xi和yi分别为式(5)在迭代I+i次后的值.

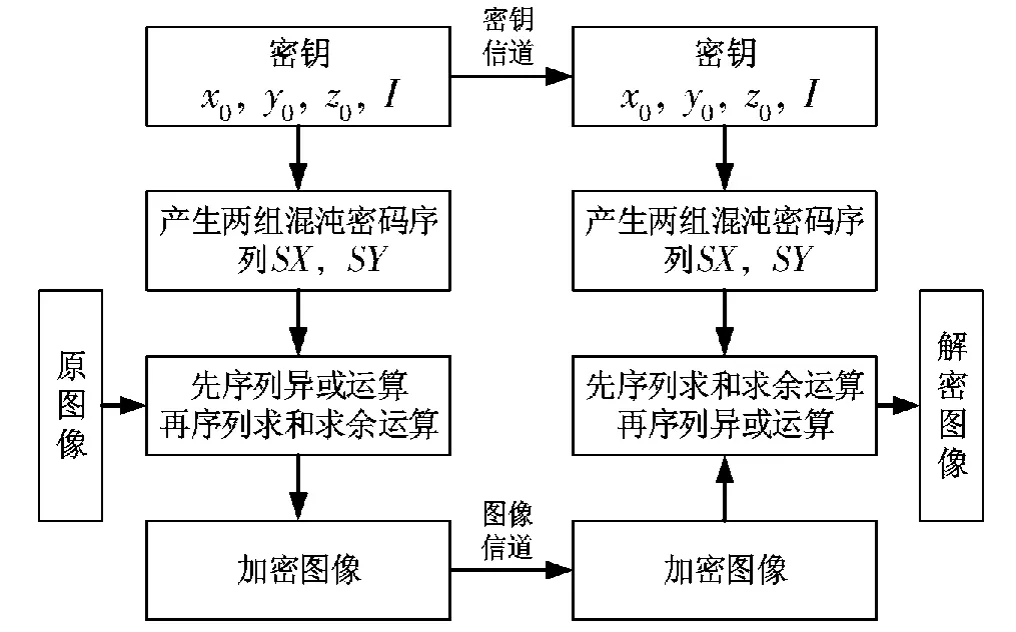
图2 加解密算法流程Fig.2 The flow chart of encryption algorithm

(2)对原图像的数据序列进行先异或运算再求和求余运算，其加密公式如下式所示:

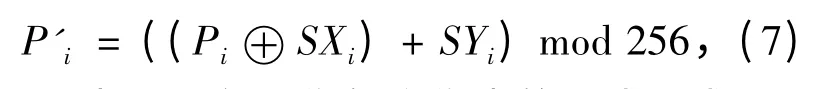
其中，Pi表示彩色图像每个像素的R或G或B分量的值，P'i为加密后的值.

解密算法是加密的逆过程，具体步骤如下:

(1)与加密过程一样，由式(5)和式(6)产生两组长度为M×N×3的一维混沌密码序列SX，SY;

(2)对加密图像的数据序列进行先求和求余运算再异或运算，其解密公式如下式所示，最后得到解密图像:

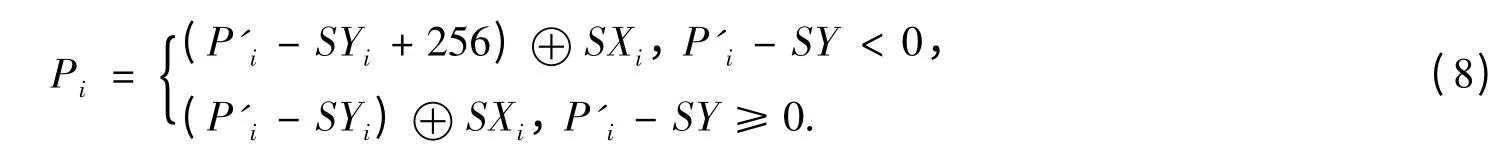
式(8)也可以写成式(9)的形式:

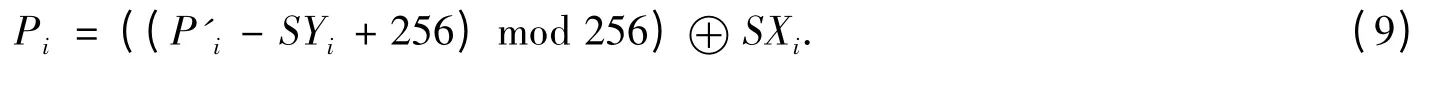
4 实验仿真与加密效果分析

以大小为256×256个灰度级、24位真彩色的Lina图像(如图3(a)所示)为实验对象，设定初始密钥值为x0=0.345 678，y0=0.578 993，z0=0.234 567，I=222，加密效果如图3(b)所示，正常解密图像如图3(c)所示，当改变密钥x0=0.345 678 1时的解密图像如图3(d)所示.可以看出，加密图像在直观上已经变得杂乱无章，即使微小改动初始密钥值，也不能获得原图像的任何信息，体现了该加密算法对密钥有较强的敏感性.

图3 图像加解密效果Fig.3 The results of encryption and decryption of images

4.1 直方图对比效果

原图像和加密图像的直方图分别如图4(a)和4(b)所示.可以看出，加密后的直方图变得非常均匀，图像的像素变化大，通过直方图信息来破解图像将会变得非常困难.

4.2 图像加密效果的评价参数

图像加密效果的评价是在原始图像与加密后的图像之间进行的.设原始图像为O，加密后的图像为E，则O(i)和E(i)分别代表各自数组中第i个元素代表的亮度值，数组的长度为n.

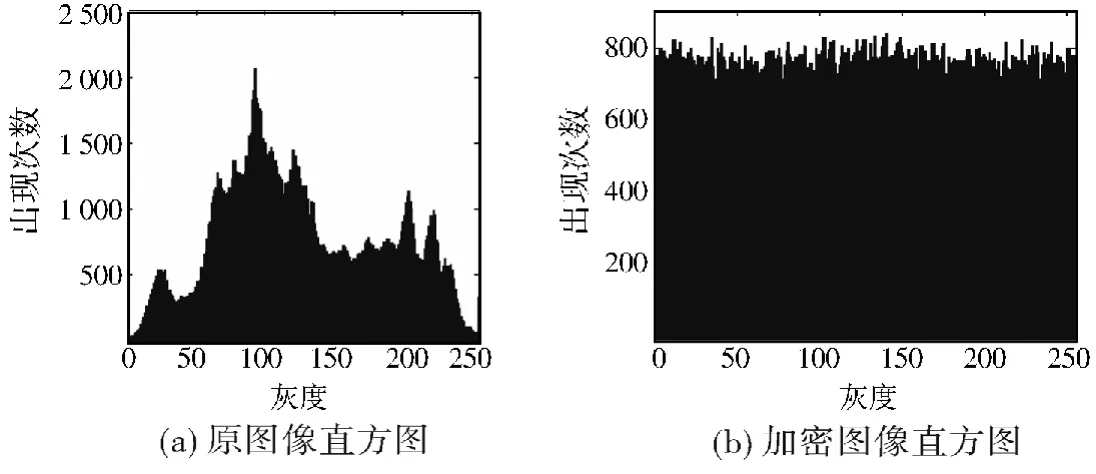
图4 原图像与加密图像的直方图Fig.4 Histogram of the original image and the effect of the encrypted image

(1)信息熵:

其中，p(xi)表示符号集中符号xi在消息中出现的概率，l表示灰度等级数，也表示符号的个数，本系统中l为256个，即为0～255.显然，信息X的不确定性越大，信息熵越高.当所有变量出现的概率都相同时，信息熵最大，本系统中的最大信息熵为log2256=8.

(2)灰度平均变化值:

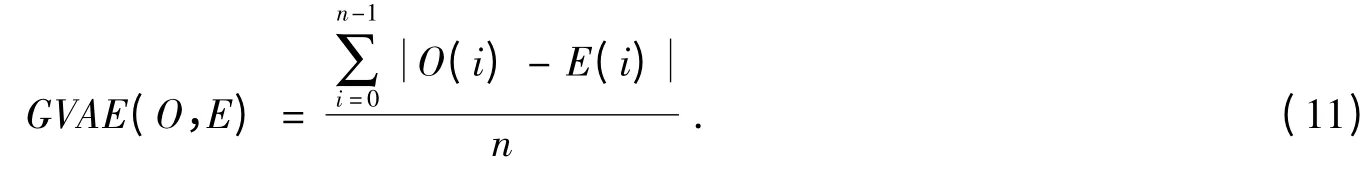
当两个图像的灰度产生均匀变化时，图像置乱的效果是最好的，并且越均匀安全性越高，最好的情况应该是图像灰度平均变化值为128.

(3)图像相似度:

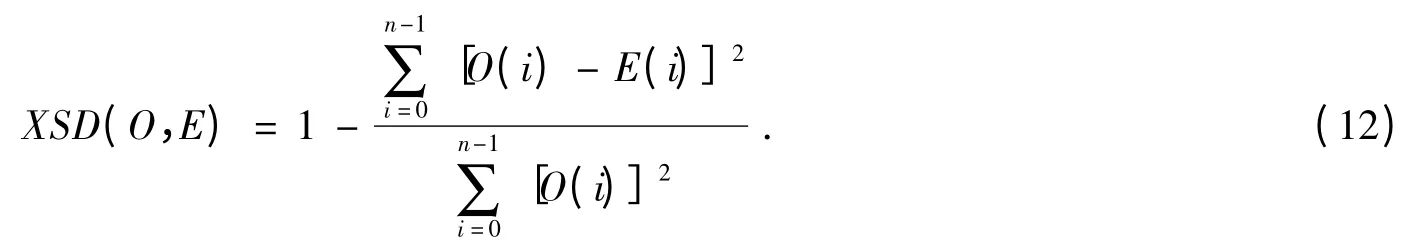
若原图像与加密图像完全相同，则其相似度为1，即完全相似.对于加密图像来说，与原图像的相似度越小，安全性就越高.以蓝色分量为例，对加密前后图像的信息熵、灰度平均变化值和图像相似度进行了统计，如表1所示.可以看出，加密后图像的信息熵大大增加，加密前后的相似度也较小，表明加密效果较好.由于算法没有涉及像素间的置乱操作，故灰度变化值不是特别大.

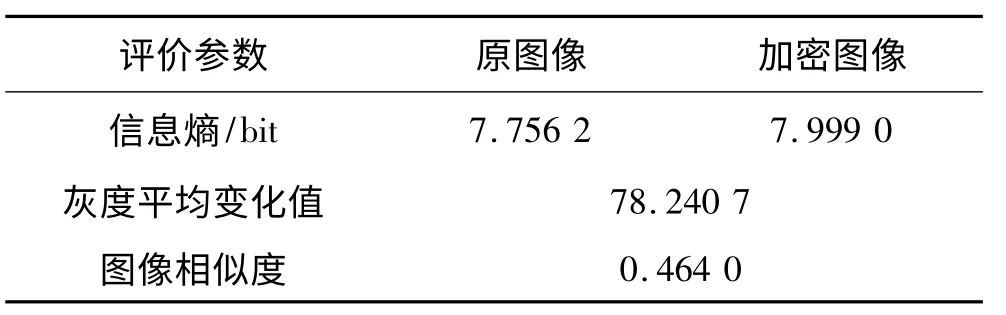
表1 算法加密效果的评价参数情况(针对蓝色分量)Tab.1 The results of evaluation parameters of encryption algorithm results(for the blue component)

4.3 抗剪裁分析

对加密后的图像(如图3(b)所示)进行1/8剪裁，如图5(a)所示，然后进行解密操作，得到解密后的图像，如图5(b)所示.可以看出，剪裁部分对未被剪裁部分图像的解密没有任何影响，表明该算法抗剪裁能力较强.

4.4 抗随机噪声

对加密后的图像如图3(b)所示，每个像素的RGB分量都增加0～20的随机值，当值超过255时以255代替，然后进行解密操作，得到解密后的图像如图6所示.可以看出，解密后的图像基本能恢复原图像的信息，但存在部分失真，这表明该算法具有一定的抗随机噪声能力.

图5 抗1/8剪裁效果分析Fig.5 The analysis of 1/8 anti-cut effectiveness

图6 抗随机噪声效果Fig.6 The effects anti-random noise

5 加密过程中的注意事项和对比

5.1 注意事项

(1)在改进的方法中，对μ进行扰动，使它不再是一个定值，这样增大了密钥空间并提高了Logistic的混沌度，使得混沌系统的相关信息不易被暴露，提高了安全度;

(2)经过改进之后，对xn，yn，zn进行处理，在统计过程中每个值都出现了一次，这说明在迭代的过程中，没有出现同样的xn，yn，zn，这解决了单纯的Logistic映射的有限精度所导致的周期循环问题;

(3)彩色图像加密算法设计应考虑以下四点基本要求:加解密速度快、Kerckhoff原则、密钥空间大、解密保真度高.

5.2 算法比较随机性检验

对传统的算法和改进后的算法做一些随机性的比较，结果见表2.

表2 传统算法与改进算法随机性检验结果对比Tab.2 The eom parison of randomness of traditional algorithm and im proved algorithm test results

由表2可知，改进后的Logistic算法通过了随机性检验试验，在产生密钥序列的随机性方面，与传统的Logistic算法相比得到了明显提高，增强了改进算法的安全性.

6 结论

(1)为了抵抗解密图像的破解攻击，需在保证加密运算速度和低资源消耗的前提下，尽量增大系统的密钥空间.因此，结合Chebychev混沌映射的值域为［-1，1］的特性，设计算法对二维Logistic混沌系统的参数μ进行迭代变化，大大增加了密钥空间.该算法在序列异或加密算法上进行了改进，改进后的算法非常简单，可以对图像数据流快速地实时加解密.

(2)彩色图像加密算法设计时应考虑以下四点基本要求:加解密速度快、Kerckhoff原则、密钥空间大、解密保真度高.在不需要压缩加密的前提下，应该尽量选择在RGB色彩模型空间或空域上进行，并且要综合考虑运行速度、抗攻击能力、密钥空间大小、抗噪声及抗剪裁能力等因素.

［1］张晓强，王蒙蒙，朱贵良，等.图像加密算法研究新进展［J］.计算机工程与科学，2012，34(5):1-6.

［2］张靓.混沌伪随机序列发生器设计及应用［D］.哈尔滨:黑龙江大学，2008.