基于平衡理论的大柔性飞行器模型降阶

孙明敏，陆宇平，徐 亮，沈华勋

（南京航空航天大学 自动化学院，江苏 南京210016）

近年来，高空长航时（HALE）飞行器因其超长续航能力日益受到重视。这类飞行器不但可以执行军事上的机载情报、监视与侦察等任务， 而且可用于民用上的网络通信以及一般大气研究[1-2]，具有广阔的应用前景和研究价值。 然而由于任务需要，理想HALE 飞行器具有机翼展弦比大、机身轻而薄的特点，大柔性飞行器（VFA）就是此类飞行器最典型的代表。VFA 的大柔性结构可能导致飞行器在常规飞行条件下发生大的变形、结构低频颤振与刚体运动耦合，以及气动失速等问题， 具有与刚体飞行器显著不同的气动弹性和飞行动力学特性[3-4]，这意味着飞行器的模型十分复杂，维数较高，且存在较多非线性，给控制设计带来困难。因此，在控制设计之前，有必要研究VFA 模型的模型降阶，便于对此类复杂系统进行理论分析，减少数据运算量。

本文采用基于平衡实现理论的平衡残差降阶方法，针对某高阶大柔性飞行器线性化模型，进行了模型降阶，并利用基于状态空间Newmark 法给出了详细的降阶模型仿真分析。

1 大柔性飞行器模型

本文研究对象是基于美国国防部高级研究计划局（DARPA）“秃鹰”计划所设计的大柔性飞行器，简称“秃鹰”模型[5]。 “秃鹰”模型的结构及坐标系如图1 所示，该飞行器拥有15 个向前的推力发动机和6 个升降舵，其中两个升降舵位于机翼两端，剩余4 个升降舵位于中间尾翼的尾部。 需注意，翼根、吊舱和发动机坐标系与惯性坐标系一致。

“秃鹰”模型是一个高保真线性动力学模型，由真实测量数据生成，在本文中基于平衡点将数据进行线性化处理，其中一个平衡点为：

模型有n=707 个状态量，m=381 个输入量和p=404 个输出量，在一个线性化单点飞行条件下，其开环线性时不变状态空间形式如下：

该模型描述了惯性空间6 自由度(x,y,z,Φ,θ,Ψ)及其速度(u,v,w,p,q,r)的动力学方程，特别之处在于模型中引入了空气来流wi、机体弹性位置xflex和弹性速度vflex：

381 个输入量中有33 个控制输入 （15 个发动机推力、6个升降舵偏转角δ、6 个偏转角速度δ˙和6 个偏转角加速度δ¨），剩余348 个输入表示阵风扰动：

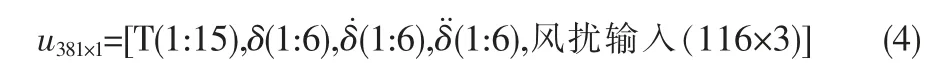
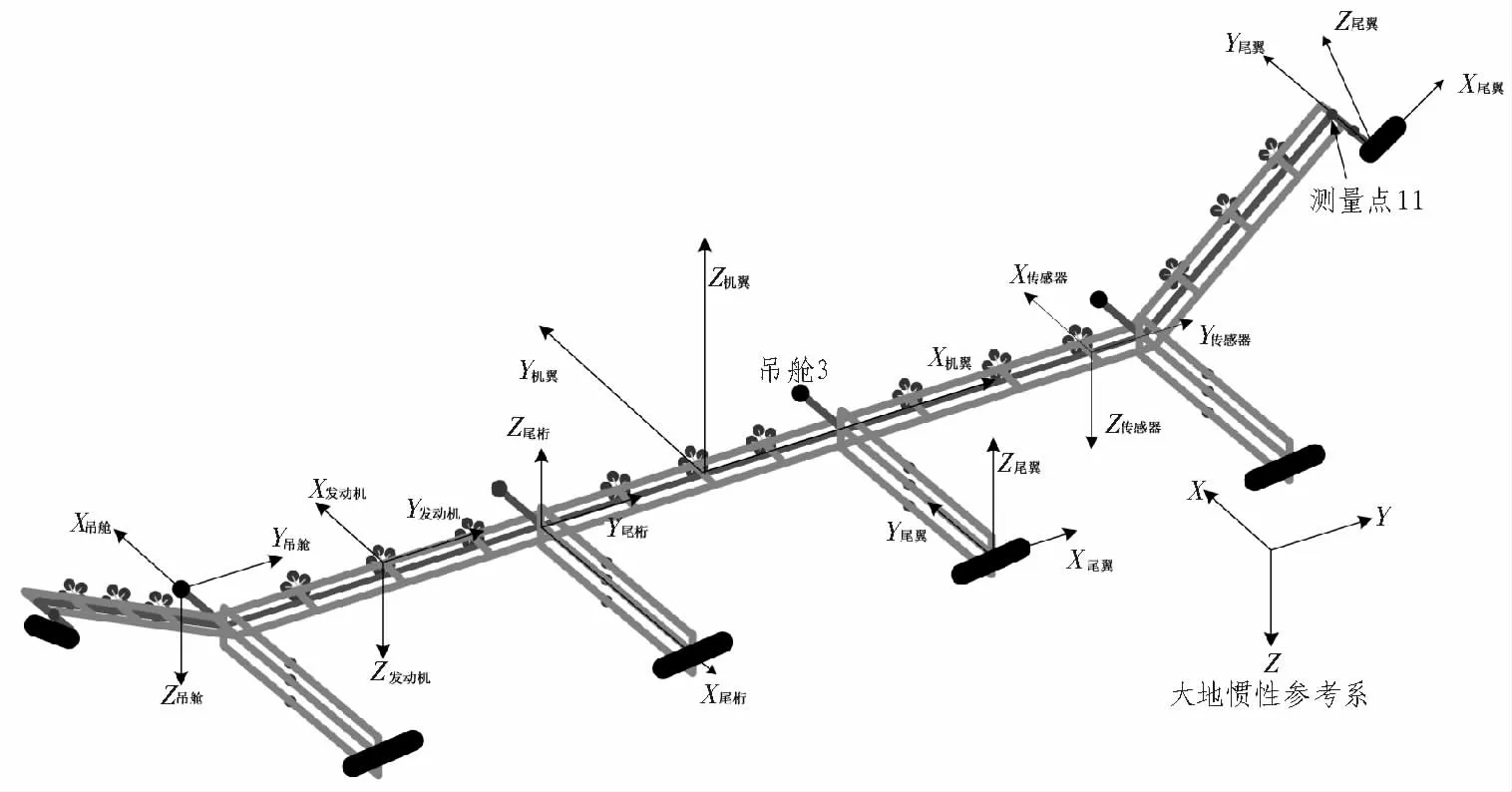
图1 “秃鹰”飞行器结构及坐标系图Fig. 1 Vehicle structure and coordinate systems for vulture

404 个输出量中，翼根传感器测量飞行器重心处的18 个变量，每个吊舱传感器测量两个变量：局部迎角和侧滑角。 每 个节点传感器测量18 个局部状态：

传统控制技术对高阶“秃鹰”模型不再适用，因此必须对其进行状态空间模型降阶，将较大系统转化为一个近似的较小系统，使得降阶模型仍能保持原模型的一些性能，便于控制器的设计。

2 模型降阶

本文主要采用基于平衡实现的平衡残差降阶方法，来简化系统模型。

2.1 平衡实现和平衡残差法

平衡实现理论主要由Moore[6]提出。 考虑如下线性时不变系统：

定义系统可控性和可观测性Gram 矩阵Wc，Wo分别为:

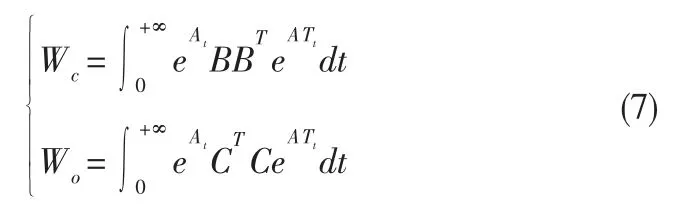
如果系统是稳定可控的，则Wc满秩；如果系统是稳定可观的，则Wo满秩。 进而可知，线性可控性和可观测性Gram 矩阵Wc，Wo是下面Lyapunov 方程的唯一正定解：

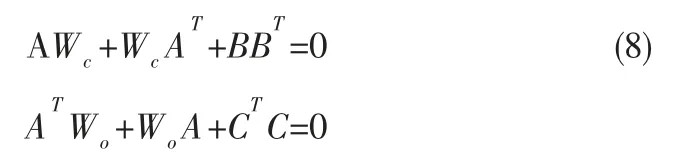
对于系统{A,B,C,D}，如果存在非奇异变换矩阵T，将原系统变换为等价系统，其中相应可控性和可观测性Gram 矩阵均为对角阵且相等，即

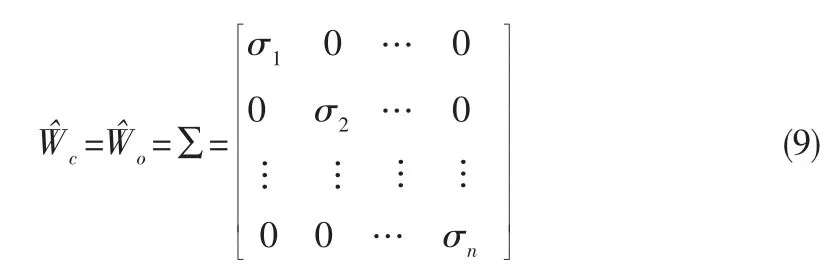
式中σ1≥σ2≥…≥σn≥0，则称}系统为原系统的平衡实现，为系统的Hankel 阵奇异值。

Hankel 阵奇异值提供了状态重要性的测度。 即大奇异值对应的状态受控制输入影响最大， 而输出也受该状态变化的影响最大。 因此，对应最大奇异值的状态影响系统输入输出行为最大。如果存在n＞r＞0，满足σr+1，σr+2，…，σn远小于σ1，σ2，σr则可将σr以后对应的状态变量进行剩余残化， 仅保留σr之前的状态。 具体方法是将平衡系统进行矩阵分块：

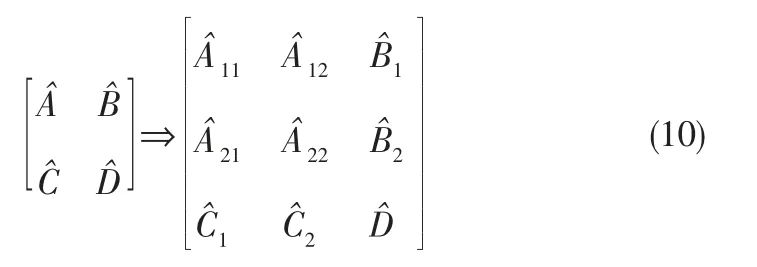
则模型降阶为

2.2 大柔性飞行器模型降阶

对于本文研究对象“秃鹰”模型，定义对象动力学模型(2)为，不考虑阵风扰动，则，取，对应于前33 个输入量的数据。设定截断值，则忽略奇异值小于的部分，保留大于的部分，对应的降阶后模型阶数为。需要注意的是，对原模型进行模型降阶前，应该先分离不稳定的模态，降阶后再把该部分加上。

图2 分别给出了原模型和降阶后模型的传递函数矩阵最大和最小奇异值。 由图可知，80 阶系统在频率低于100 Hz 时与原模型曲线基本一致，充分保持了原系统特性。

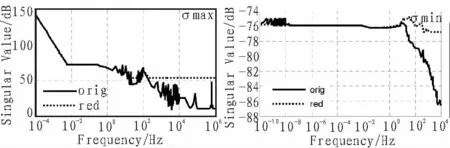
图2 原模型和降阶模型传函矩阵最大、最小奇异值对比Fig. 2 Comparison of the maximum and minimum singular values of the transfer function matrix between the original model and the reduced－order model

3 状态空间Newmark 法求解方程

本文研究系统为一阶线性方程组， 由于该系统方程维数过大，而Matlab 中常用的四阶龙格－卡塔等算法精度虽高，但求解过程太过复杂，时间太长，在求解该线性系统模型时1 小时只能完成1 s 时间仿真运算。 且在运算中最好采取变步长算法，若设置定步长大于0.000 1 s 时，在运算一段时间后会出现计算错误无法求解情况。 因此需要选择合适的一阶微分求解方法进行数值运算， 这里采用基于平均速度的状态空间Newmark 求解法[7]，具体方法如下。

通过引入状态空间向量，一个一般动力学系统的二阶微分方程可以写成以下一阶状态空间方程形式：

其中，设定{q}=[{x˙}，{x}]T为状态向量，{x}为位移向量，[A]为系统运动矩阵，{F}为力向量，[A]和{F}的具体形式如下：

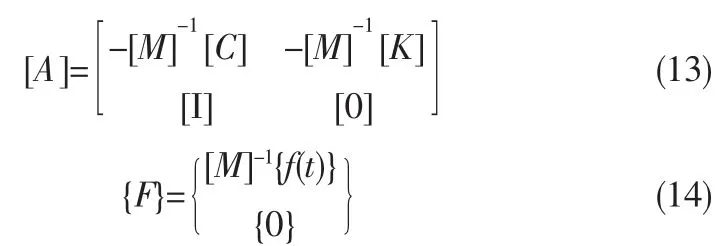
[M]，[C]，[K]分别为系统的惯性、阻尼和刚度矩阵，{f(t)}为外力向量。 如图3 所示，在时间tn和tn+1（或者步长和）的间隔△t 间定义新的变量τ(0≤τ≤△t，定义内平均速度{q˙(t)}为：

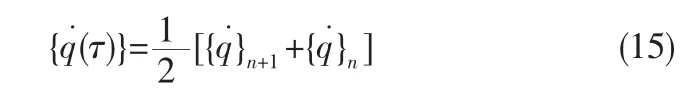
令τ=0 时，{q(τ)}={q}n则

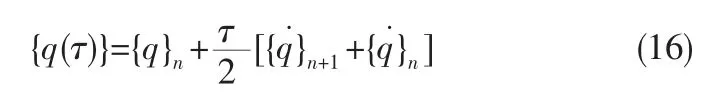
根据以上方程，令τ=△t 或t=tn+1，有

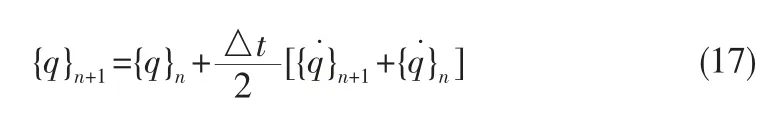
图3 状态空间Newmark 法的平均速度示意图Fig. 3 Constant average velocity for the state－space newmark method

则时刻的速度微分方程为

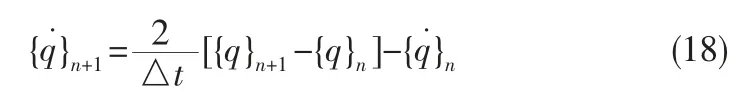
将原始一阶方程代入上式，可以得到tn+1时刻速度的解

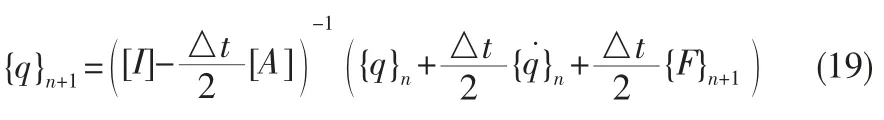
由于本文所研究模型已经是一阶线性模型， 故状态向量即为，则

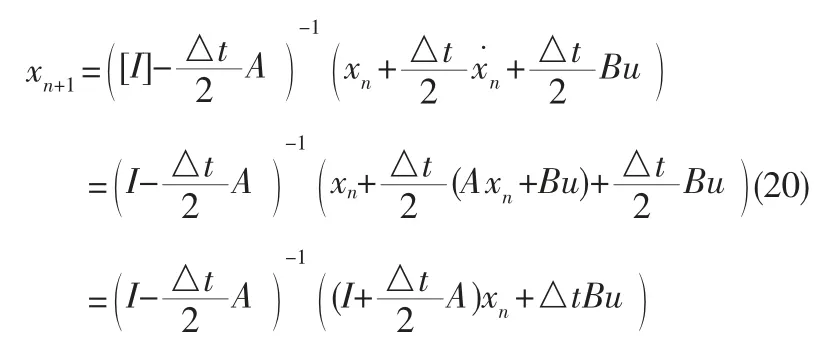
由以上表达式可知第时刻的速度可以由第时刻的速度求得，这种基于平均速度的Newmark 方法比传统方法更简单直观， 具有很高的可靠性和准确性， 且更容易在软件程序中实现。 实验证明此方法求解方程精度较高，与使用四阶龙格－库塔法求解结果几乎没有差别， 但是运算时间要比龙格－库塔法快至少100 倍，非常适用于高阶微分方程的求解。

4 仿真分析

下面给定相同输入条件，对80 阶降阶系统和原系统输出曲线进行对比分析。

假设起始时刻飞行器处于静稳定状态, 令均匀分布于主翼的15 个发动机在0～10 s 同时产生10lbs 的推力，仿真时间30 s， 则飞行器受到均匀推力作用时的输出曲线如图4～6 所示，其中翼根处测量的是飞行器质心的状态量，吊舱3 和测量点11 的位置见图1。

施加向前推力主要影响飞行器纵向运动特性， 水平速度增大，则升力增大，垂直速度随之变大，高度上升（翼根坐标系中向下为正）；飞行器首先产生抬头力矩，随着升力增大产生负的俯仰力矩使得迎角减小。由于推力均匀施加在主翼上，横侧向运动主要是由机翼各模块相互耦合作用的， 受推力直接影响不大。

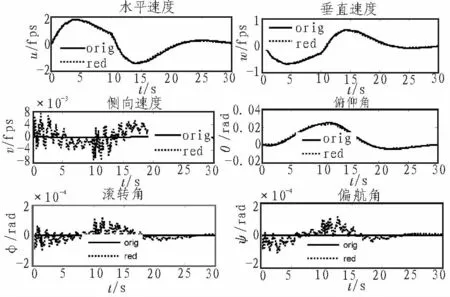
图4 飞行器翼根处速度及角度变化曲线Fig. 4 Velocities and angles measured at the wing root

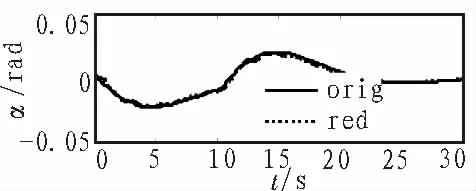
图5 吊舱3 处迎角变化曲线Fig. 5 Angle of attack measured at the pod 3

图6 测量点11 处速度变化曲线Fig. 6 Velocities measured at the point 11

由仿真曲线可知，在推力作用下，降阶模型的纵向和垂直方向速度、角度、迎角等特性变化与原模型基本一致，且符合理论分析结果。仿真曲线中侧向运动幅度较小，且受耦合作用影响，振荡频率较大；对比原模型和降阶模型侧向运动可知，虽然两者差别较大， 但是相对整个飞行器模型影响很小。 可见，降阶模型能够保持原飞行器系统的运动特性，效果较好，满足精度要求。

5 结论

本文在忽略阵风扰动的情况下，利用基于平衡实现的平衡残差方法，对某高保真大柔性飞行器模型进行了模型降阶，同时针对此高阶模型， 运用基于平均速度的状态空间Newmark 法求解方程[8]，给出原系统和降阶系统的输出响应分析。仿真结果表明，采用平衡残差法能得到近似度较高的降阶模型，对比原系统模型，降阶模型能够很好地反映飞行器系统的纵向和横侧向响应特性，且误差很小，验证了上述降阶方法的可行性。 此外，仿真结果与理论分析的定性比较，从一定程度上证明了模型的正确性。 本文的结果可为下一步基于大柔性飞行器控制系统的设计提供参考。

[1] Shearer C M,Cesnik C E S.Nonlinear flight dynamics of very flexible aircraft[J].Journal of Aircraft,2007,5(44):1528-1545.

[2] Whitson S. The Proteus, Giving Shape to Form Unknown [J].Private Pilot, 1988-12, 33(12): 44-50.

[3] 谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2005, 29(12): 1087-1090.XIE Chang-chuan,WU Zhi -gang,YANG Chao.Aeroelastic analysis of large aspect ratio wing [J].Journal of Beijing University of Aeronautics and Astronautics, 2005, 29(12): 1087-1090.

[4] Shearer C M. Coupled Nonlinear Aeroelasticity and Flight Dynamics of Fully Flexible Aircraft[D]. Michigan: University of Michigan,2008.

[5] Gadient R,Wise K,Lavretsky E.Very flexible aircraft control challenge problem[C]//Guidance,Navigation, and Control and Co -located Conferences, Minneapolis, Minnesota, AIAA,2012,4793:1-6.

[6] Moor B C. Principal component analysis in linear systems:Controllability, observability, and model reduction [J]. IEEE Transactions on Computer -Aided Design of Integrated Circuits and Systems, 1998,17(8): 645-654.

[7] Byung Ok Kim, An SungLee. A transient response analysis in the state-space applying the average velocity concept[J].Journal of Sound and Vibration, 2005,281: 1023-1035.

[8] 田传艳， 胡军照， 杨黔龙，等.滑翔航弹半实物实时仿真软件的设计[J].现代应用物理， 2014（3）：239-244.TIAN Chuan-yan，HU Jun-zhao，YANG Qian-long，et al.A hardware-in-the-loop real time simulation software for the gliding missile[J].Modern Applied Physics ， 2014（3）：239-244.