基于ANSYS的港口起重机桁架结构的优化设计
2015-08-25王文志滕媛媛
王文志,刘 龙,滕媛媛
(上海海事大学物流工程学院,上海201306)
基于ANSYS的港口起重机桁架结构的优化设计
王文志,刘龙,滕媛媛
(上海海事大学物流工程学院,上海201306)
随着航运的发展,港口起重机也迅速发展。目前,不仅要求起重机有更高的起重量和起升高度,还要求起重机的重量轻、作业空间大。为了减轻自重、简化设计方法,应用ANSYS优化模块提供的一阶优化方法对起重机桁架结构优化,优化后起重机自重减小23.2%,质量明显减小。
桁架结构;ANSYS;优化设计;自重
DOI:10.3969/j.issn.1009-9492.2015.01.013
0 引言
随着港口运输行业的发展,港口起重机的起升高度和外伸梁长度不断增加,从而质量越来越大,但这对码头的承载能力是个巨大的考验,为了在满足刚度强度和稳定性的前提下减轻自重,需要对起重机的结构进行优化设计,ANSYS为优化设计提供了比较好的优化方法。在ANSYS优化模块的帮助下,刘大强[1]等曾对起重机整体金属结构进行优化;刘成鑫[2]曾对门座起重机的四连杆组合臂架系统进行结构优化;马玉英[3]对起重船拔杆式起重机臂架结构进行拓扑优化;戚其松[4]等对门式起重机主梁进行优化设计,减重效果明显。桁架结构由于具有自重轻、造价较低和迎风面积小等诸多优点,广泛应用于各种工程领域,包括航空航天、桥梁建筑、车辆、起重机械等[5]。
本文基于APDL语言的有限元分析方法,对起重机桁架结构拉杆的外径、鞍梁的高度和拉杆与梁节点的位置的优化,从而在部分结构上减轻起重机整体自重,并且小车在满载时压杆的稳定性满足要求,得到比较满意的结果。
1 ANSYS的优化设计介绍
1.1 ANSYS介绍
ANSYS分析软件提供了两种工作模式:人工交互方式(GUI方式)和命令流输入方式(Batch方式)。人工交互方式对于复杂的有限元模型,由于对模型修改后分析带来的大量重复操作,占据了大量的时间,有时是计算时间的几倍。另外,采用GUI方式往往生成大量数据文件,这造成了交流的不便。
APDL允许复杂的数据输入,使用户实际上对任何设计或分析属性有控制权,可以减少大量的重复工作,特别适用于经少量修改后需多次重复计算的场合。同时便于保存数据,建立模型时间短,运算时间短,节省时间[6]。
1.2 ANSYS优化介绍
ANSYS优化具体步骤如下。
(1)生成分析文件:①参数化建模;②加载与求解;③进入ANSYS的后处理模块。
(2)提取对应参数。在ANSYS结果数据库里提取与分析文件中变量相对应的参数,一般为状态变量和目标函数。
(3)进入优化设计处理器,指定分析文件。
(4)声明优化变量。即指定设计变量(优化对象)、状态变量(约束条件)和目标函数(质量、面积、体积、应力、费用等)。ANSYS允许有不超过60个设计变量(DV)和不超过100个状态变量(SV),但只能有1个目标函数(OBJ)。
(5)选择优化工具或方法。ANSYS提供了两种优化方法:零阶方法和一阶方法。这两种优化方法可以处理绝大多数的优化问题。零阶方法(直接法)之所以称为零阶方法是由于它只用到因变量而不用到它的偏导数。零阶方法是一个很完善的处理方法,使用所有因变量的逼近,可以很有效地处理大多数的工程问题。一阶方法(间接法)基于目标函数对设计变量的敏感程度,使用偏导数,即使用因变量的一阶导数。此方法精度很高,设计空间也相对较大,结果精确,但一阶方法计算量大。
对于这两种方法,ANSYS提供了一系列的分析—评估—修正的循环过程。就是对于初始设计进行分析,对分析的结果就设计要求进行评估,然后修正设计。这一循环过程重复进行直到所有的设计要求都满足为止[7]。
(6)指定优化循环控制方式。每种优化方法和工具都有相应的循环控制参数,如最大迭代次数等。
(7)进行优化分析。所有的控制选项设定后即可进行分析。在优化过程中,优化循环文件(Jobname.LOOP)会根据分析文件生成。循环在满足下列任一情况时终止∶收敛、中断(不收敛,但最大循环次数或是最大不可行解数目达到了)、分析完成[8-9]。
2 岸桥桁架结构有限元模型
2.1桁架结构参数
起重机在静止满载的情况下,小车在大梁上行走给起重机施加载荷,如图1。起重机梁跨距为96.3 m,总高为28.4 m,额定承载65 t。桁架结构材料选用Q345钢,弹性模量为E=205 GPa,由于在计算过程中忽略了筋、螺钉等元件,故设梁的密度为14 000 kg/m3,拉杆的密度为9 000 kg/m3,腿的密度为16 000 kg/m3。强度要求是梁所受的轴应力不能超过其许用轴应力100 MPa,拉杆应力不超过其许用值265.4 MPa,梁上两个节点之间的最大挠度不能超过这两个节点距离的1/500。
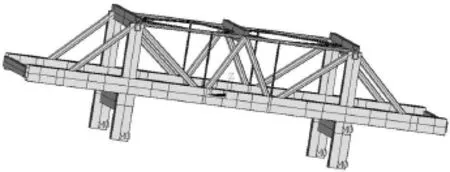
图1 起重机桁架结构
2.2参数化建模
在参数化建模过程中,选用beam188单元作为仿真的单元材料。Beam188单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。Beam188是三维线性(2节点)或者二次梁单元。每个节点有六个或者七个自由度,自由度的个数取决于KEYOPT(1)的值。当KEYOPT(1)=0(缺省)时,每个节点有六个自由度;节点坐标系的x、y、z方向的平动和绕x、y、z轴的转动。当KEYOPT(1)=1时,每个节点有七个自由度,这时引入了第七个自由度(横截面的翘曲)。这个单元非常适合线性、大角度转动和/并非线性大应变问题。当NLGEOM打开的时候,beam188的应力刚化,在任何分析中都是缺省项。建模时,铰接的地方,在ANSYS中采用耦合重合点并释放自由度的方法来实现。
2.3约束与施加载荷
该结构在施加约束时,采用比较理想化的约束方法,由于考虑到是在静止情况下优化桁架结构,故假设起重机大车部位三个自由度完全约束。施加载荷时,刚腿承受固定载荷为10吨,柔腿承受固定载荷为5吨。在优化过程中选取9个的特殊的位置加载分析桁架受力变形情况。将小车自重及货物的重量通过4个车轮施加4个集中载荷,每个载荷为37.5 kN,这是由于在满载情况下,小车自重与吊具和满载起重量之和为150 t。
2.4求解
在计算过程中,先计算一组载荷,提取这组需要数据,然后清空施加的载荷,再施加下组载荷,计算并提取数据,一直进行直至9组计算完毕。优化时利用桁架所承受的支反力与加速度比值获得质量WT。
3 优化设计的模型
3.1优化变量
优化设计是通过构建优化模型,运用各种优化方法,通过满足设计要求下的迭代次数,求得目标函数的极值,得到最优设计方案。
其数学模型可表示为:
目标函数:WT=FZ/g
设计变量:7≤H≤15
0.02≤D≤0.074
10≤B≤20
状态变量:SDi≤100 MPa(i=1,2,3,……,54)
SMAXj≤265.4 MPa(j=1,2,…..9)
DZMAXn≤L/500(L是梁上两节点的距离)(n=1,2,3,4,5)
其中,桁架系统重量WT为目标函数,用来评价设计方案的优劣,拉杆轴应力SDi、梁的轴应力SMAXj、节点挠度DZMAXn为状态变量,只有满足状态变量的要求的设计才是合理设计。桁架高度H、梁上铰接点距中心的距离B、拉杆圆管外径D是设计需要优选参数组成的变量,为设计变量。
3.2优化结果
为了提高优化精度,优化方法采用一阶优化,优化前后结果比较如表1。
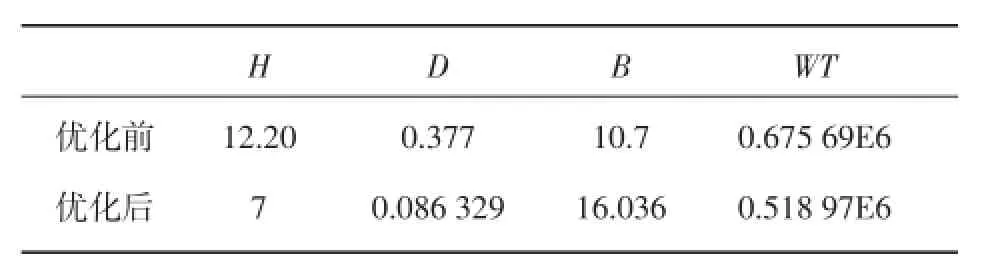
表1 R优化结果
优化过程的最优解H=7 m,D=86.329 mm,B=16.036 m,WT=518.97 t。
一阶算法下目标函数和设计变量的历程如图2。
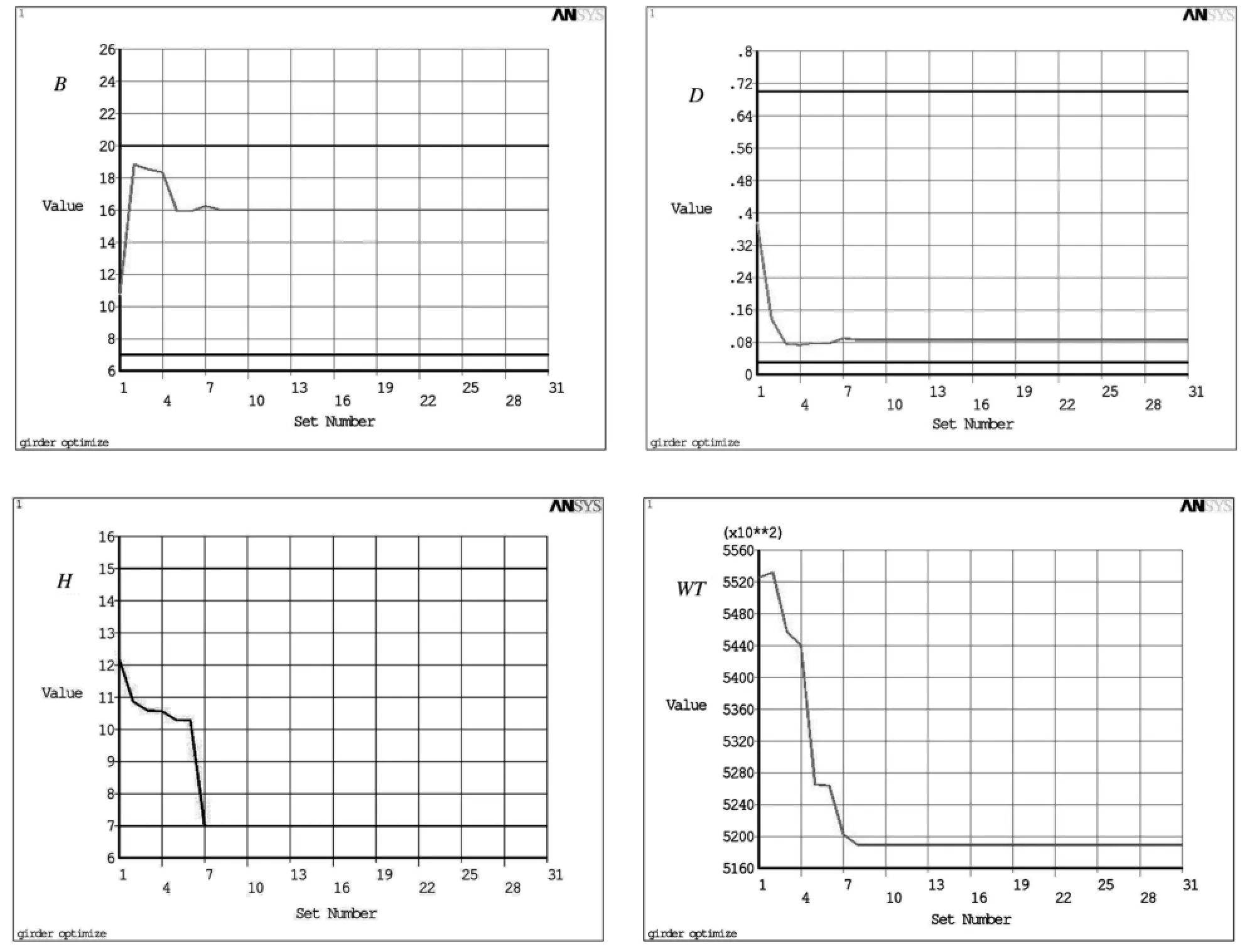
图2 各变量及质量历程曲线
3.3压杆稳定性校核
由于桁架结构的对称性,在提取拉杆应力的时候选取一半作为研究对象。如图3,选取杆66,59,58,62,63,68作为研究对象。初始桁架高H=11.3 m,节点距中心的距离B=15.06 m,管的外径D=0.377 m。
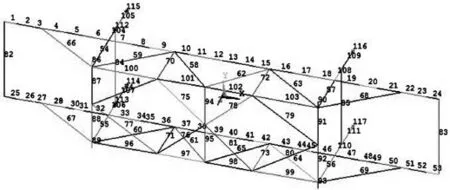
图3 桁架结构标号图
由Ansys提取的轴应力可以看出杆件59,63,66,68受压。当加载在点113,114,134,135节点时,其中杆66的压应力最大为σ=94.33 MPa。为了校核其稳定性,采用ANSYS屈曲分析。
屈曲分析是一种用于确定结构开始变的不稳定时的临界载荷和屈曲模态形状的技术。ANSYS提供了非线性屈曲分析和特征值(线性)屈曲分析两种方法,特征值屈曲分析即教科书里传统的弹性屈曲分析方法,非线性屈曲方法比特征值屈曲分析更精确,是实际中更常用的方法。分析66杆的稳定性用特征值法,是线性屈曲分析,主要有两大步骤:先进行结构静应力分析,分析时必须将预应力开关打开;然后进行屈曲分析[10]。
在建立模型时,采用beam188单元,分析结果显示屈曲系数为1 322 700,由于静力分析时为结构施加的载荷为单位载荷,所以受压杆临界压力为1 322 700 N,其应力为96.5 MPa,与解析解基本一致。由于结构中最大应力为94.33 MPa,故杆稳定。
在加载左侧的时候,杆件66承受最大压应力,当加载右侧和中间位置的时候杆件67承受最大压应力,由于桁架结构的对称性,杆件66和67具有相同的稳定性系数。当加载113,114,134,135节点时,杆67承受最大压应力σ= 94.33 MPa。由此可知杆67稳定。综上可知,杆在小车的运动过程中处于稳定状态。
4 总结展望
基于有限元软件ANSYS对桁架结构的优化分析,在满足桁架结构自身要求的前提下,优化方案比原方案自重减少了23.2%。在小车满载的情况下,各拉杆在受压时能够保持其稳定性,并且梁的刚度符合要求,优化效果明显。将优化的结果应用于实际,在很大程度上节省了结构的成本和结构设计的周期,使得设计的桁架结构更加的经济化,合理化和科学化,该种分析桁架结构的优化方法对于其他结构的优化设计具有一定的参考价值。
在优化过程中,将梁和拉杆作了理想化假设,在进步研究工作中要考虑到具体的情况,比如梁上加筋,还有螺栓对梁的影响以及满足疲劳强度条件。同时,还需要考虑更合适的优化方法,保证优化结果的精度和可靠性。
[1]刘大强,徐洪泽,冷松.岸边集装箱起重机结构优化分析[C].第八届物流工程学术年会论文集,2008.
[2]刘成鑫.港口门座起重机四连杆组合臂架结构优化设计研究[D].武汉:武汉理工大学,2013.
[3]马玉英.大型起重船臂架结构拓扑优化设计研究[D].天津:天津大学,2007.
[4]戚其松,范小宁,徐格宁,等.基于Ansys的门式起重机主梁优化设计[J].起重运输机械,2013(8):32-34.
[5]魏文儒,屈福政.基于ANSYS的空间桁架结构拓扑优化设计[J].起重运输机械,2008(7):32-34.
[6]张东宝.单梁双吊钩门式起重机结构分析与优化设计[D].西安:长安大学,2011.
[7]张红松,胡仁喜,康工廷.ANSYS12.0有限元分析从入门到精通[M].北京:机械工业出版社,2010.
[8]金梁斌.辊压自动化传输设备桥式起重机吊架力学特性研究[J].机电工程技术,2014(3):19-22.
[9]曾志华,虞伟建.ANSYS结构优化技术在机械设计中的应用[J].现代设计与先进制造技术,2009,13(38):33-36.
[10]高耀东,李强,张玉宝,等.ANSYS机械工程应用精华60例:第4版[M].北京:电子工业出版社,2012.
(编辑:阮毅)
Optimization Design of the Port Crane Truss Structure Based on ANSYS
WANG Wen-zhi,LIU Long,TENG Yuan-yuan
(Logistics Engineering,Shanghai Maritime University,Shanghai201306,China)
Port crane is the guarantee of port industry development At present,it not only requires the crane having a higher weight and hoisting height,besides,the port crane weight must be light and the optimize space is large.This optimization design mainly through reduces the weight of crane truss optimization.ANSYS optimization module provides two optimization methods-zero order and first order,which can deal with most questions.Beam axial stress,the deflection of beam and the stability of the pressure rod as state variables of optimization are to be considered in the optimization.Quality as the objective function,reduced greately after optimization.
truss structure;ANSYS;optimization design;self weight
TH215
A
1009-9492(2015)01-0052-04
2014-07-10
王文志,男,1989年生,山东临沂人,硕士。研究领域:港口机械。
